Learning Algorithms

CSI 4106 - Fall 2025

Marcel Turcotte

Version: Sep 9, 2025 15:56

Preamble

Message of the Day

Large language models exhibit remarkable linguistic capabilities, prompting an increasing number of individuals to engage in personal dialogues with them. Murray Shanahan, affiliated with Google DeepMind and Imperial College, introduces an compelling framework for examining the “behavior” of these models. He conceptualizes their interactions through the lens of role play, as discussed in his recent work published in Nature.

• Consciousness, reasoning and the philosophy of AI with Murray Shanahan, in this Google DeepMind podcast, Hannah Fry interviews Murray Shanahan, 2025-04-24.

Depending on the context of their interaction prompts, these models can adopt personas that simulate malevolent individuals, potentially offering advice with harmful consequences.

• OpenAI Eagerly Trying To Reduce AI Psychosis And Squash Co-Creation Of Human-AI Delusions When Using ChatGPT And GPT-5, by Lance Eliot, Forbes, 2025-09-02.
• What to know about ‘AI psychosis’ and the effect of AI chatbots on mental health, PBS News, 2025-08-31.

Here is a reminder for the University of Ottawa’s wellness page, which offers a comprehensive array of resources, including medical and mental health-care services, designed to support your well-being and that of those around you.

• Student Health and Wellness

Microsoft boss troubled by rise in reports of ‘AI psychosis’, BBC News, 2025-08-21.

Learning outcomes

• Differentiate between model, objective, and optimizer in learning algorithms.
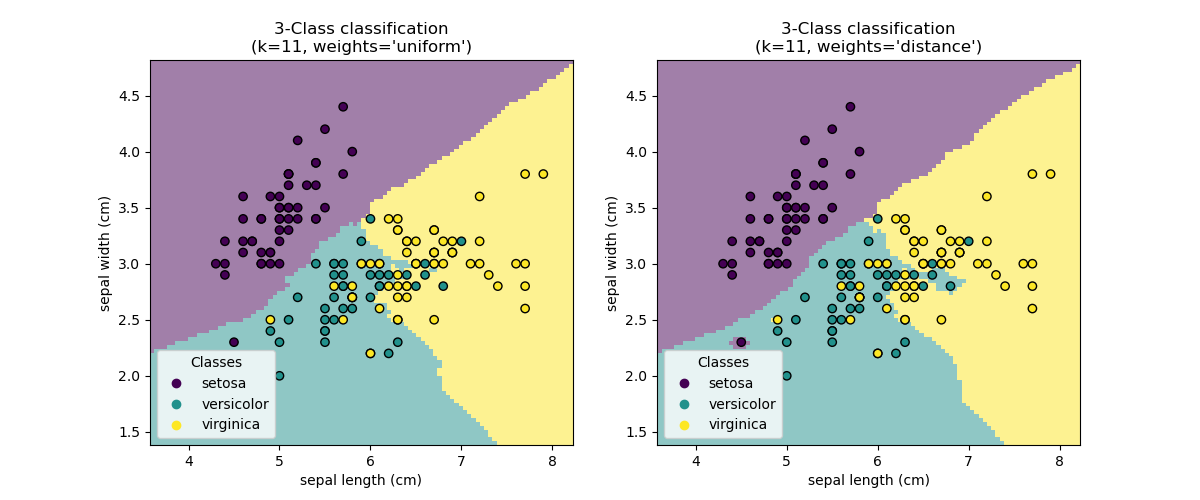
• Explain KNN for classification and regression, including uniform and distance-weighted prediction.
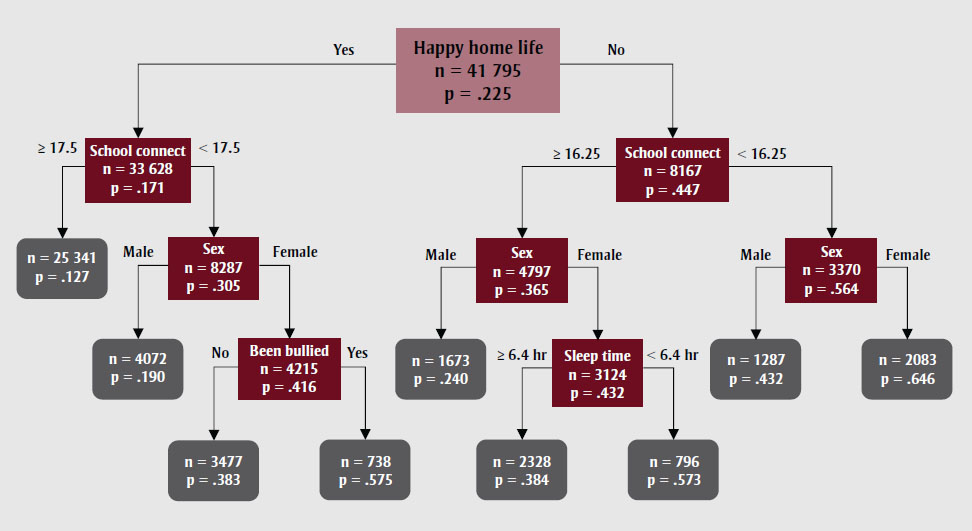
• Describe decision trees and apply the split criterion using impurity measures such as Gini.
• Interpret decision boundaries and the concept of linear separability.
• Formulate linear regression with an intercept/bias term and evaluate it using RMSE.

KNN

k-nearest neighbours

• KNeighborsClassifier, examples
• KNeighborsRegressor, exemples

As indicated in the introductory lecture, I aim to present a series of concepts leading to deep learning. As a starting point, linear regression would be a logical choice as a primary learning algorithm to examine. Nonetheless, it is equally critical to possess a high-level understanding of various other learning algorithms, as they differ significantly in model structures and training processes. Therefore, I will briefly discuss k-nearest neighbours and decision trees, before introducing linear regression.

The k-nearest neighbour (KNN) algorithm is a simple, non-parametric, instance-based learning method used for classification and regression. It classifies a data point based on the majority label of its \(k\) nearest neighbours in the feature space, where \(k\) is a user-defined constant. Distance metrics like Euclidean distance are commonly used to determine the nearest neighbours. In the re

In the context of regression, the predicted value \(\hat{y}(x)\) is calculated as a weighted sum of the labels of its \(k\) nearest neighbours. The weights can be uniform or based on distance, reflecting the proximity of each neighbour to the query point \(x\).

For a query point \(x\), let its \(k\) nearest neighbours have targets \(y_1, \dots, y_k\) and distances \(d_1, \dots, d_k\).

• Uniform weights (default):

\[ \hat{y}(x) = \frac{1}{k} \sum_{i=1}^k y_i \]

• Distance weights (the built-in option "distance"):

\[ \hat{y}(x) = \frac{\sum_{i=1}^k \frac{1}{d_i} \, y_i}{\sum_{i=1}^k \frac{1}{d_i}} \]

In the above, as the distance \(d_i\) between the example \(x_i\) and the example \(x\) increases, the reciprocal \(\frac{1}{d_i}\) decreases. Consequently, examples that are farther from \(x\) exert less influence on the predicted outcome, \(\hat{y}(x)\).

In both cases, convex combination property guarantees that:

\[ \min(y_1, \dots, y_k) \;\; \leq \;\; \hat{y}(x) \;\; \leq \;\; \max(y_1, \dots, y_k). \]

A non-parametric algorithm does not make any assumptions about the underlying data distribution and does not learn a fixed set of parameters or a model during the training phase. Instead, it relies directly on the training data to make decisions at the time of classification or regression, making it flexible and adaptive to various data shapes but potentially computationally expensive at prediction time.

KNN has clear limitations:

1. Computational cost
   • Prediction requires computing distances to all training points, \(O(n)\) per query.
2. Curse of dimensionality
   • In high-dimensional spaces, distance metrics lose discriminative power.
3. Choice of \(k\) and distance metric
   • Small \(k\): high variance, sensitive to noise/outliers.
   • Large \(k\): high bias, oversmoothing.
4. Sensitivity to feature scaling
   • Distances are scale-dependent; variables with larger ranges dominate unless features are normalized/standardized.
5. Imbalanced data
   • In classification, if one class is much more frequent, KNN can be biased toward that class since neighbours are more likely to belong to it.
6. Not extrapolative
   • Predictions are always convex combinations (in regression) or majority votes (in classification) of training labels.
   • This means KNN cannot extrapolate trends outside the range of observed training data.

In scikit-learn, several models are commonly used for regression tasks. Here are some of the main models:

1. Linear Regression (LinearRegression):
   • A simple linear approach that models the relationship between the independent variables and the dependent variable by fitting a linear equation to the observed data.
2. Support Vector Regression (SVR):
   • An extension of Support Vector Machines (SVM) for regression tasks, which tries to fit the best line within a specified margin of tolerance.
3. Decision Tree Regression (DecisionTreeRegressor):
   • Uses decision trees to model the relationship between the input features and the target variable by recursively splitting the data into subsets.
4. Random Forest Regression (RandomForestRegressor):
   • An ensemble method that uses multiple decision trees to improve predictive accuracy and control overfitting.
5. Gradient Boosting Regression (GradientBoostingRegressor):
   • Another ensemble method that builds sequential decision trees, where each tree corrects the errors of the previous one.
6. K-Nearest Neighbors Regression (KNeighborsRegressor):
   • A non-parametric method that predicts the target variable based on the average of the k-nearest neighbours in the feature space.

These models offer a range of approaches to handle different types of regression problems, each with its own strengths and suitable applications.

Attribution: Nearest Neighbors Classification.

Decision Tree

Interpretable

Decision trees are valuable because they clearly delineate the rules learned by the model. The decision tree above illustrates the results of a study examining clinically significant anxiety symptoms. In this instance, the initial determinant was whether students reported having a positive home environment.

Attribution: Public Health Agency of Canada

What is a Decision Tree?

• A decision tree is a hierarchical structure represented as a directed acyclic graph, used for classification and regression tasks.
• Each internal node performs a binary test on a particular feature (\(j\)), such as evaluating whether the number of connections at a school surpasses a specified threshold.
• The leaves function as decision nodes.

Decision trees can extend beyond binary splits, as exemplified by algorithms like ID3, which accommodate nodes with multiple children.

The tree’s structure is inferred (learnt) from the training data.

Classifying New Instances (Inference)

• Begin at the root node of the decision tree. Proceed by answering a sequence of binary questions until a leaf node is reached. The label associated with this leaf denotes the classification of the instance.
• Alternatively, some algorithms may store a probability distribution at the leaf, representing the fraction of training samples corresponding to each class \(k\), across all possible classes \(k\).

When a decision tree is used to solve a regression task, each leaf node stores a prediction value. Specifically:

\[ \hat{y}_\text{leaf} = \frac{1}{N_\text{leaf}} \sum_{i \in \text{leaf}} y_i, \]

where \(N_\text{leaf}\) is the number of training samples that ended up in that leaf, and \(y_i\) are their target values.

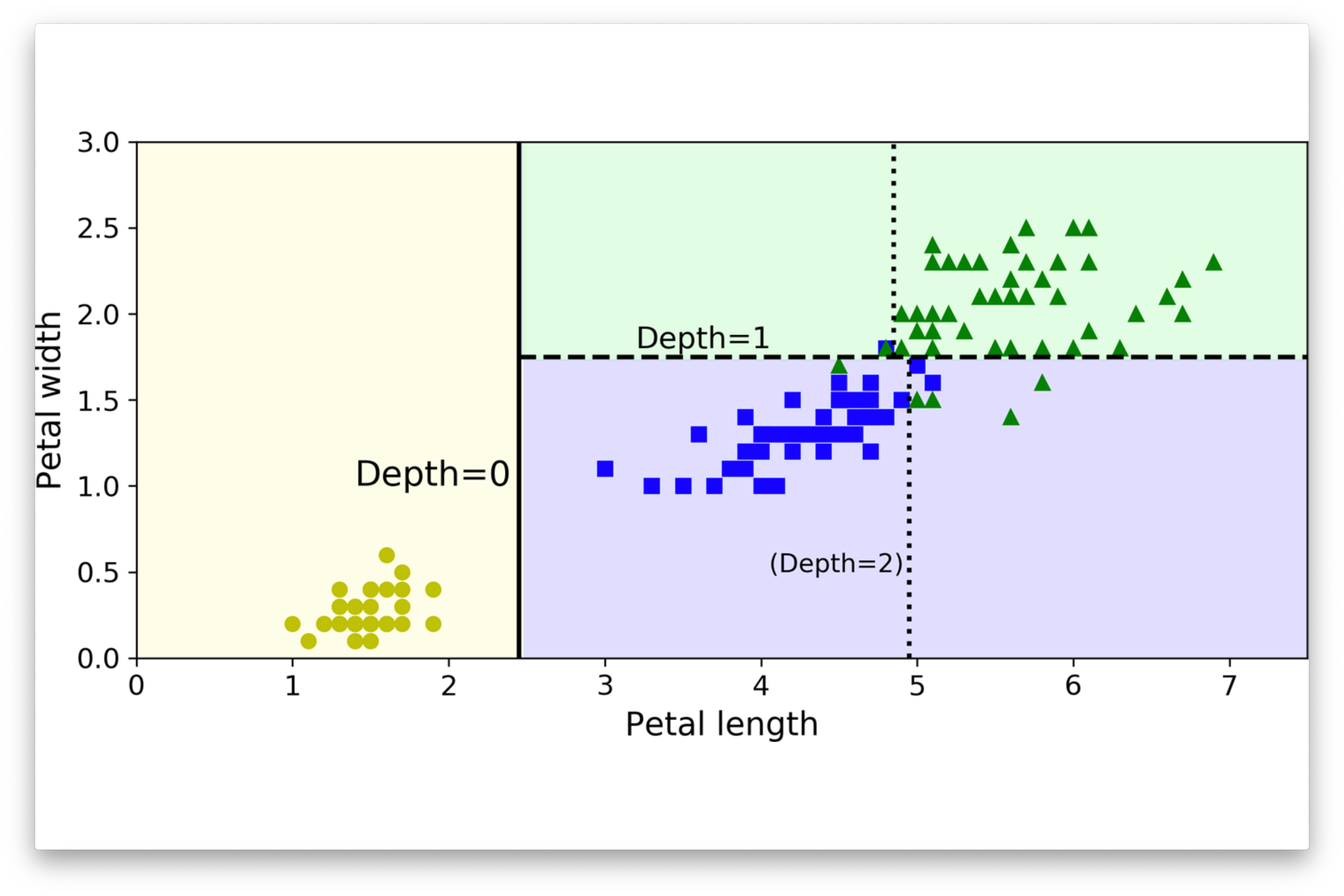
Decision Boundary

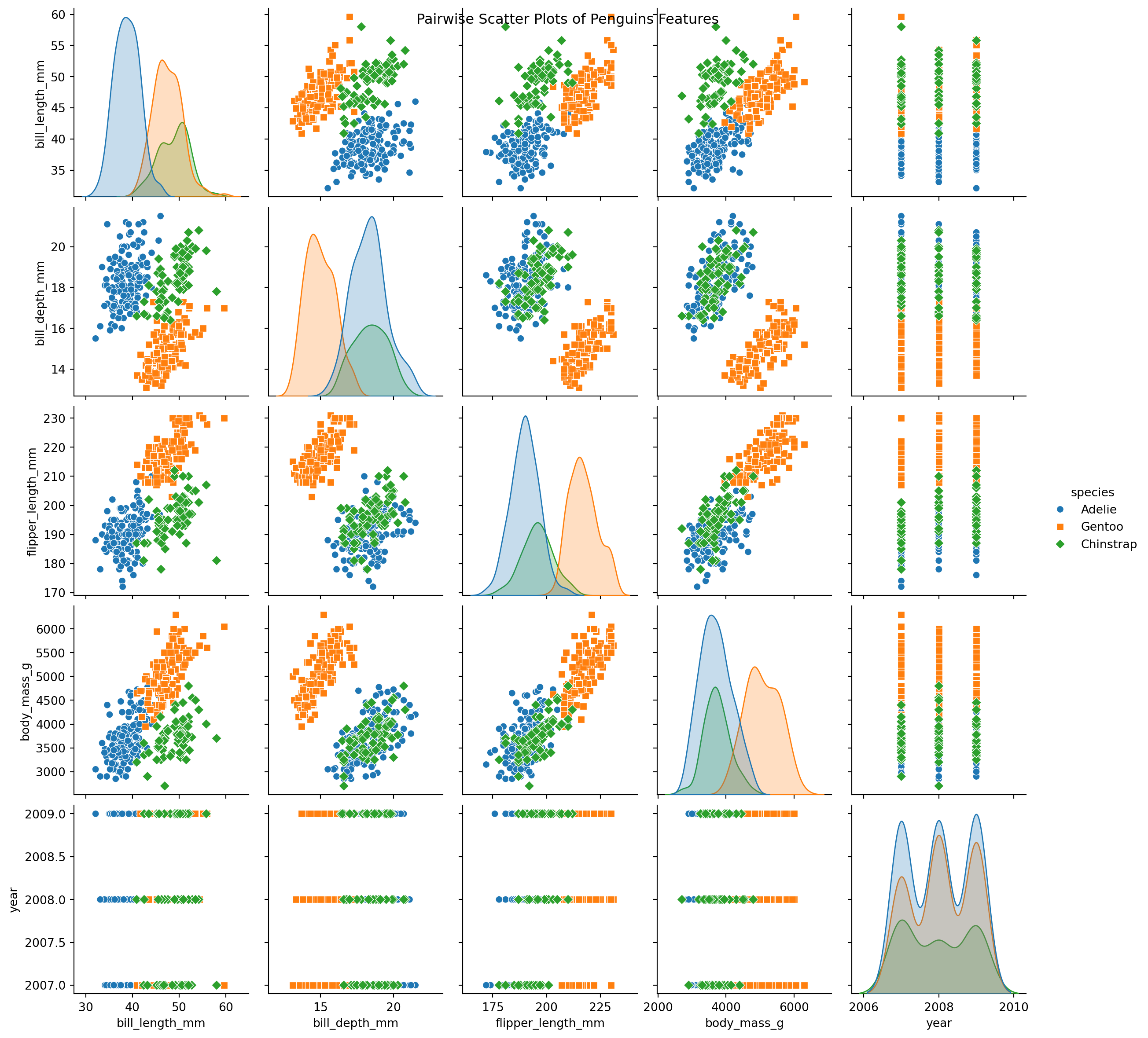
Palmer Pinguins Dataset

# Loading our dataset

try:
  from palmerpenguins import load_penguins
except:
  ! pip install palmerpenguins
  from palmerpenguins import load_penguins

penguins = load_penguins()

# Pairplot using seaborn

import matplotlib.pyplot as plt
import seaborn as sns

sns.pairplot(penguins, hue='species', markers=["o", "s", "D"])
plt.suptitle("Pairwise Scatter Plots of Penguins Features")
plt.show()

Palmer Pinguins Dataset

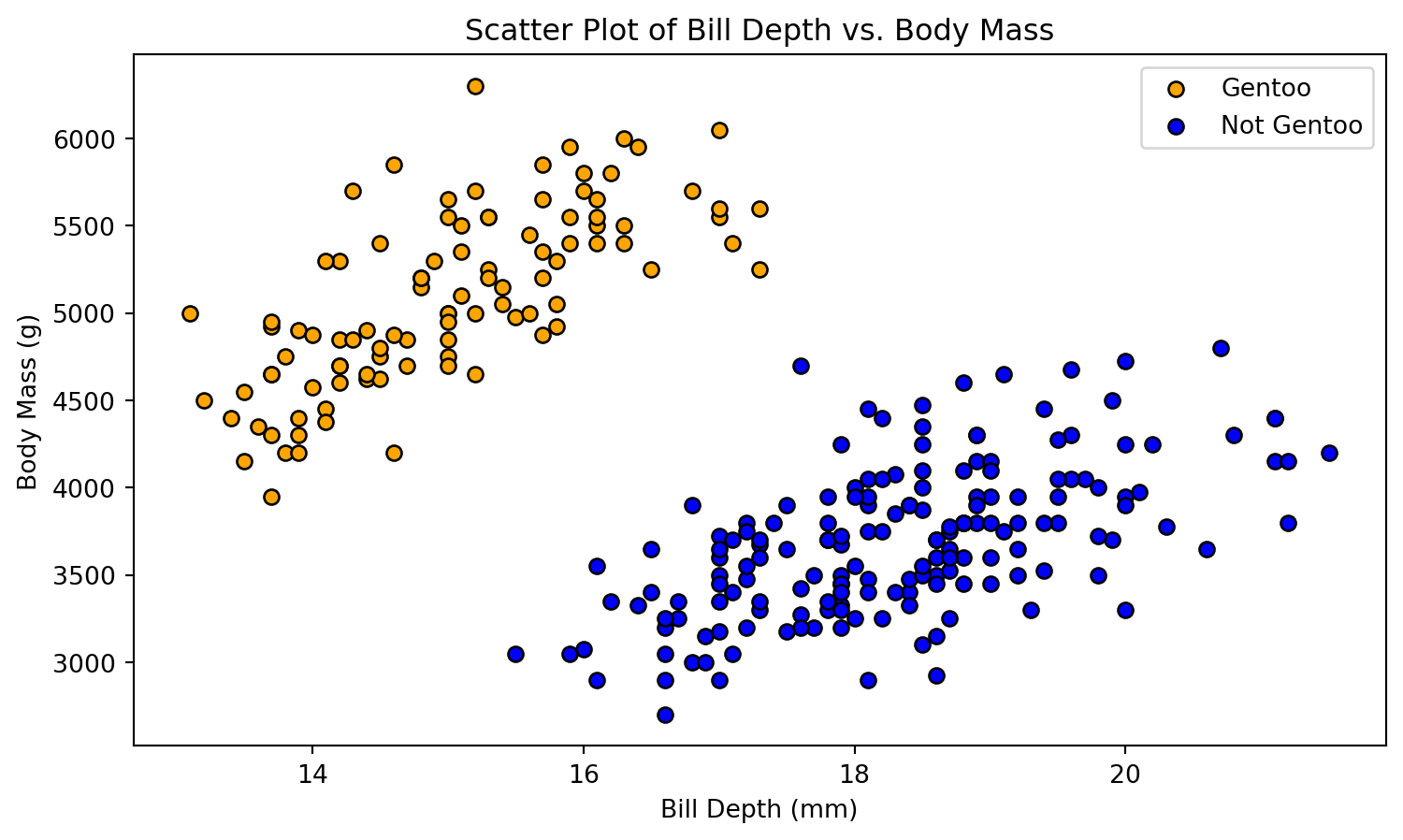
Binary Classification Problem

• Several scatter plots reveal a distinct clustering of Gentoo instances.
• To illustrate our next exemple, we propose a binary classification model: Gentoo versus non-Gentoo.
• Our analysis will concentrate on two key features: body mass and bill depth.

Definition

A decision boundary is a “boundary” that partitions the underlying feature space into regions corresponding to different class labels.

The term boundary will be clarified over the next slides.

Decision Boundary

The decision boundary between these attributes can be represented as a line.

# Import necessary libraries
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split

try:
  from palmerpenguins import load_penguins
except:
  ! pip install palmerpenguins
  from palmerpenguins import load_penguins

# Load the Palmer Penguins dataset
df = load_penguins()

# Preserve only the necessary features: 'bill_depth_mm' and 'body_mass_g'
features = ['bill_depth_mm', 'body_mass_g']
df = df[features + ['species']]

# Drop rows with missing values
df.dropna(inplace=True)

# Create a binary problem: 'Gentoo' vs 'Not Gentoo'
df['species_binary'] = df['species'].apply(lambda x: 1 if x == 'Gentoo' else 0)

# Define feature matrix X and target vector y
X = df[features].values
y = df['species_binary'].values

# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Function to plot initial scatter of data
def plot_scatter(X, y):
    plt.figure(figsize=(9, 5))
    plt.scatter(X[y == 1, 0], X[y == 1, 1], color='orange', edgecolors='k', marker='o', label='Gentoo')
    plt.scatter(X[y == 0, 0], X[y == 0, 1], color='blue', edgecolors='k', marker='o', label='Not Gentoo')
    plt.xlabel('Bill Depth (mm)')
    plt.ylabel('Body Mass (g)')
    plt.title('Scatter Plot of Bill Depth vs. Body Mass')
    plt.legend()
    plt.show()
    
# Plot the initial scatter plot
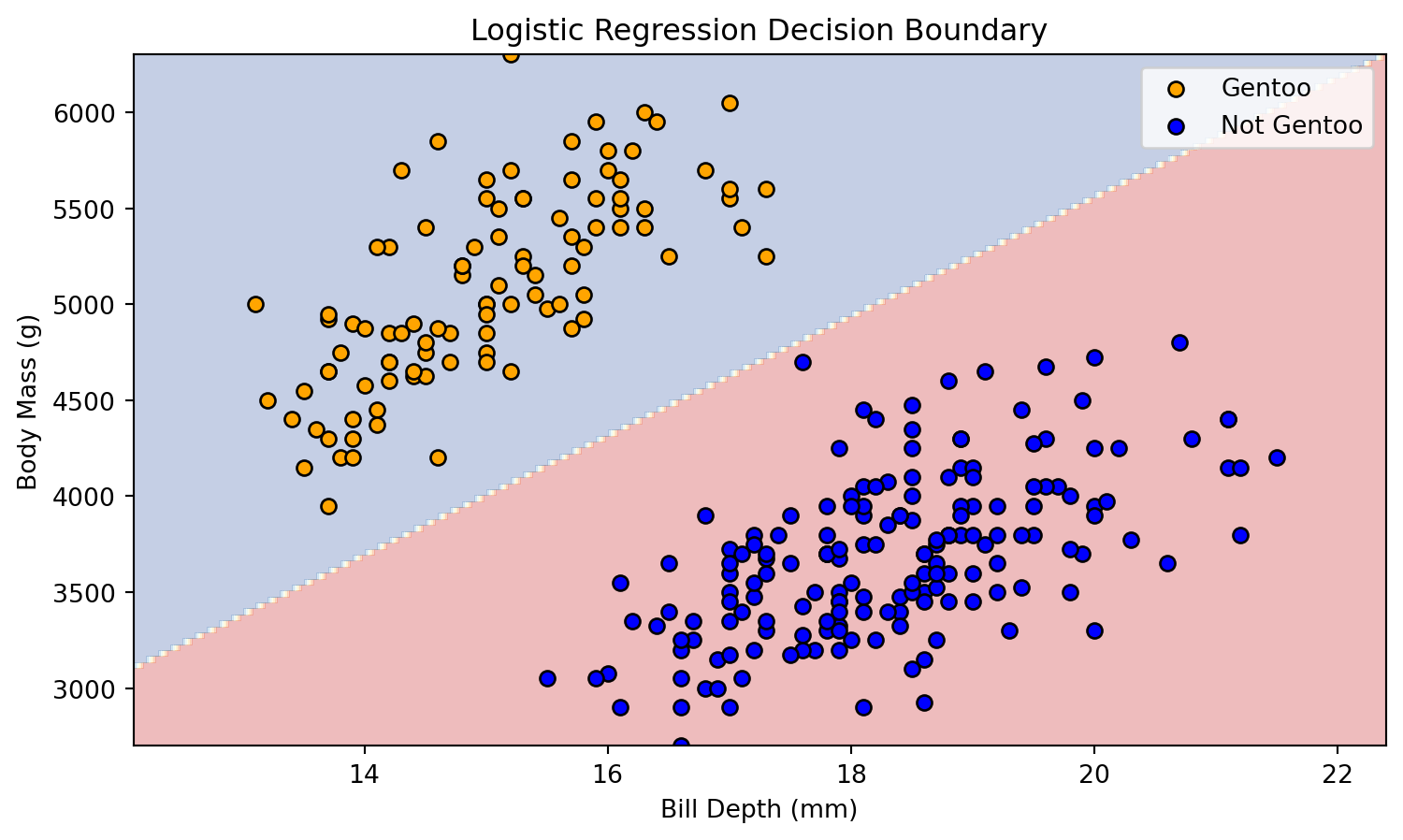
plot_scatter(X_train, y_train)

Decision Boundary

Decision Boundary

The decision boundary between these attributes can be represented as a line.

# Train a logistic regression model
model = LogisticRegression()
model.fit(X_train, y_train)

# Function to plot decision boundary
def plot_decision_boundary(X, y, model):
    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),
                         np.arange(y_min, y_max, 0.1))
    Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    
    plt.figure(figsize=(9, 5))
    plt.contourf(xx, yy, Z, alpha=0.3, cmap='RdYlBu')
    plt.scatter(X[y == 1, 0], X[y == 1, 1], color='orange', edgecolors='k', marker='o', label='Gentoo')
    plt.scatter(X[y == 0, 0], X[y == 0, 1], color='blue', edgecolors='k', marker='o', label='Not Gentoo')
    plt.xlabel('Bill Depth (mm)')
    plt.ylabel('Body Mass (g)')
    plt.title('Logistic Regression Decision Boundary')
    plt.legend()
    plt.show()

# Plot the decision boundary on the training set
plot_decision_boundary(X_train, y_train, model)

Decision Boundary

Definition

We say that the data is linearly separable when two classes of data can be perfectly separated by a single linear boundary, such as a line in two-dimensional space or a hyperplane in higher dimensions.

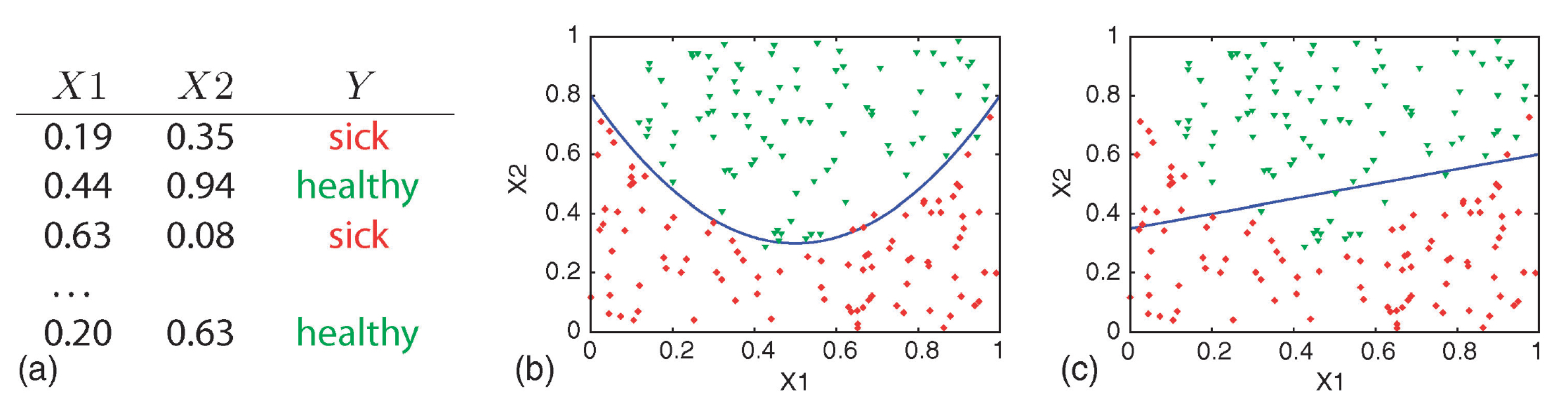
Simple Decision Doundary

(a) training data, (b) quadratic curve, and (c) linear function.

Attribution: (Geurts, Irrthum, and Wehenkel 2009)

The table on the left presents training data for a hypothetical binary classification task in a medical context, where the two attributes, \(X_1\) and \(X_2\), are used to predict the target variable, \(y\), which can take on two values: sick and healthy. You can imagine that \(X_1\) and \(X_2\) are measurements, such as blood pressure and heart rate or cholesterol and glucose levels.

Logistic regression (c) employs a linear decision boundary. In this specific example, the decision boundary is represented by a straight line. Employing logistic regression for this problem results in several classification errors: red dots above the line, which should be classified as ‘sick’, are incorrectly predicted as ‘healthy’. Conversely, green dots below the line, which should be classified as ‘healthy’, are incorrectly predicted as ‘sick’.

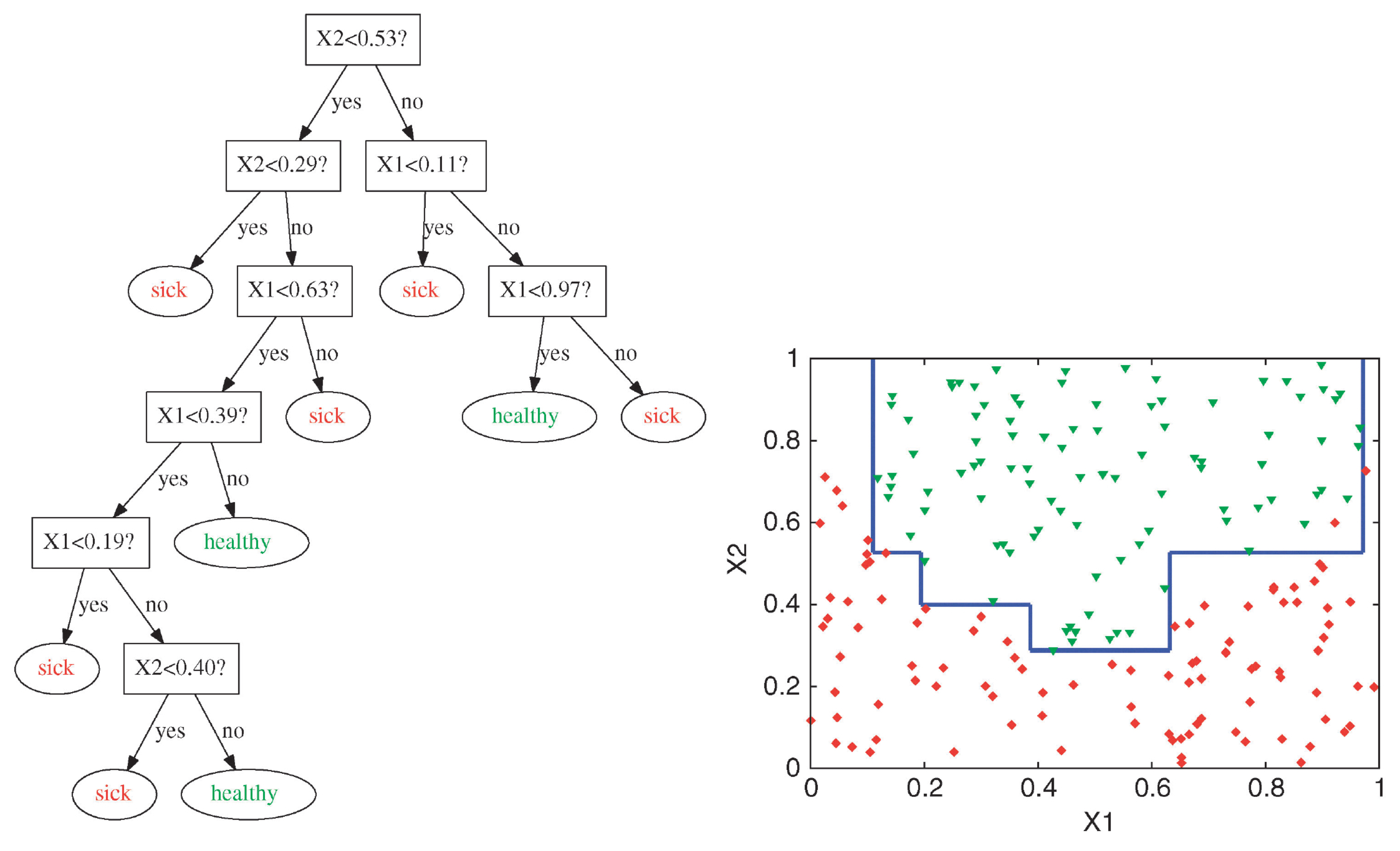
Complex Decision Boundary

Decision trees are capable of generating irregular and non-linear decision boundaries.

Attribution: ibidem.

Make sure to understand the relationships between the eight decision rules delineated in the decision tree and the nine line segments represented in the scatter plot.

Definition (revised)

A decision boundary is a hypersurface that partitions the underlying feature space into regions corresponding to different class labels.

Decision Tree (contd)

Constructing a Decision Tree

• How to construct (learnt) a decision tree?

• Are there some trees that are “better” than others?

• Is it feasible to construct an optimal decision tree with computational efficiency?

(Hyafil and Rivest 1976)

Optimality

• Let \(X = \{x_1, \ldots, x_n\}\) be a finite set of objects.
• Let \(\mathcal{T} = \{T_1, \ldots, T_t\}\) be a finite set of tests.
• For each object and test, we have:
  • \(T_i(x_j)\) is either true or false.
• An optimal tree is one that completely identifies all the objects in \(X\) and \(|T|\) is minimum.

(Hyafil and Rivest 1976)

Constructing a Decision Tree

• Iterative development: Initiate with an empty tree. Progressively introduce nodes, each informed by the training dataset, continuing until the dataset is completely classified or alternative termination criteria, such as maximum tree depth, are met.

Learning is the process of building the tree from training data.

Constructing a Decision Tree

• Initial Node Construction:
  • To establish the root node, evaluate all available \(D\) features.
    • For each feature, assess various threshold values derived from the observed data within the training set.

Constructing a Decision Tree

• For a numerical feature, the algorithm considers all possible split points (thresholds) in the feature’s range.
• These split points are typically the midpoints between two consecutive, sorted unique values of the feature.

Constructing a Decision Tree

• For a categorical feature with \(k\) unique values, the algorithm considers all possible ways of splitting the categories into two groups.
• For instance, if the feature (forecast) has values, ‘Rainy’, ‘Cloudy’, and ‘Sunny’, it evaluates the following splits:
  • \(\{\mathrm{Rainy}\}\) vs. \(\{\mathrm{Cloudy}, \mathrm{Sunny}\}\),
  • \(\{\mathrm{Cloudy}\}\) vs. \(\{\mathrm{Rainy}, \mathrm{Sunny}\}\) ,
  • \(\{\mathrm{Sunny}\}\) vs. \(\{\mathrm{Rainy}, \mathrm{Cloudy}\}\).

Evaluation

What defines a “good” data split?

• \(\{\mathrm{Rainy}\}\) vs. \(\{\mathrm{Cloudy}, \mathrm{Sunny}\}\) : \([20,10,5]\) and \([10,10,15]\).
• \(\{\mathrm{Cloudy}\}\) vs. \(\{\mathrm{Rainy}, \mathrm{Sunny}\}\) : \([40,0,0]\) and \([0,30,0]\).

Where \([20,10,5]\) indicates that the subgroup contains 20 examples of the ‘Poor’, 10 for ‘Average’, and 5 for ‘Excellent’, for our predictive model to classify the likelihood of a successful fishing day.

Evaluation

• Heterogeneity (also referred to as impurity) and homogeneity are critical metrics for evaluating the composition of resulting data partitions.

• Optimally, each of these partitions should contain data entries from a single class to achieve maximum homogeneity.

• Entropy and the Gini index are two widely utilized metrics for assessing these characteristics.

Evalution

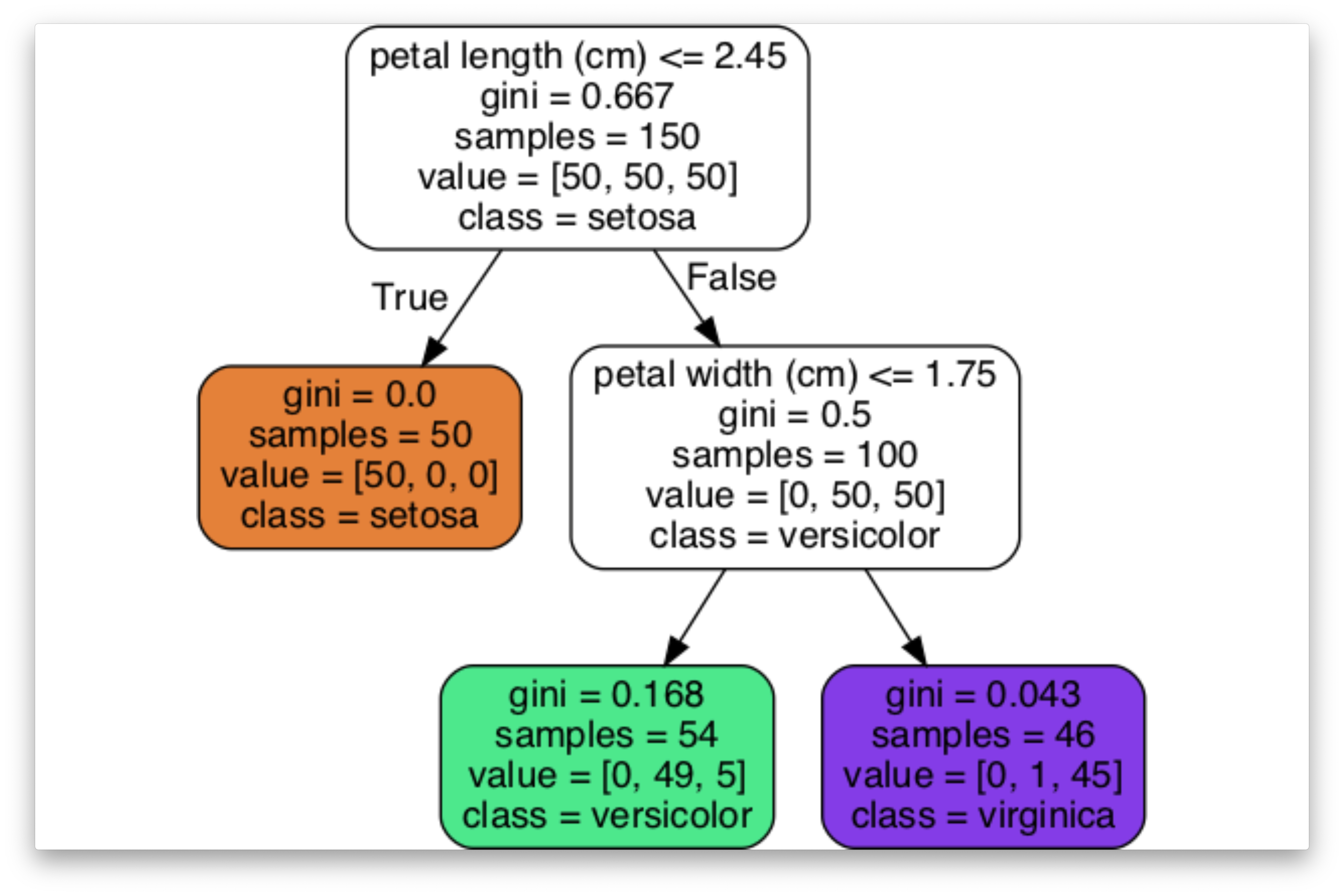
Objective function for sklearn.tree.DecisionTreeClassifier (CART):

\[ J(k,t_k) = \frac{m_{\text{left}}}{m} G_{\text{left}} + \frac{m_{\text{right}}}{m} G_{\text{right}} \]

• The cost of partitioning the data using feature \(k\) and threshold \(t_k\).

• \(m_{\text{left}}\) and \(m_{\text{right}}\) is the number of examples in the left and right subsets, respectively, and \(m\) is the number of examples before splitting the data.

• \(G_{\text{left}}\) and \(G_{\text{right}}\) is the impurity of the left and right subsets, respectively.

What would happen \(J\) had been defined as \(J(k,t_k) = G_{\text{left}} + G_{\text{right}}\)?

The split criterion is a weighted average of child impurities; weighting by node size prevents the tree from favoring splits that isolate only a few samples.

Minimize or maximize \(J\)?

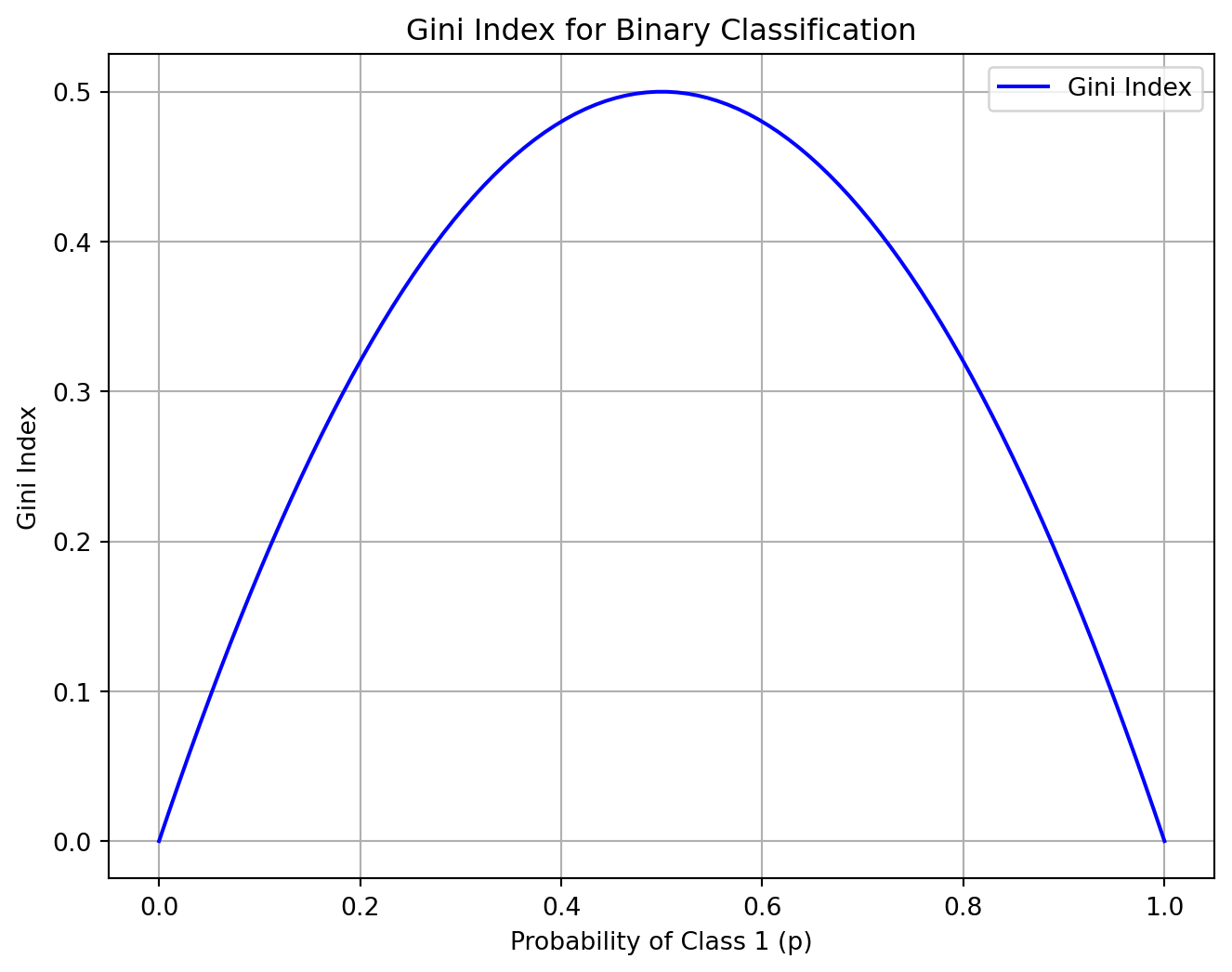
Gini Index

• Gini index (default)

\[ G_i = 1 - \sum_{k=1}^n p_{i,k}^2 \]

• \(p_{i,k}\) is the proportion of the examples from this class \(k\) in the node \(i\).

• What is the maximum value of the Gini index?

• The value of the Gini index is maximum when all the classes are equiprobable, i.e. the proportions are the same.

• For a binary classification, \(1 - \[\frac{1}{2}^2 + \frac{1}{2}^2] = 0.5\).

• For the general case, \(1 - n \times \frac{1}{n}^2 = 1 - \frac{1}{n}\), as \(n \to \infty\), the Gini index tends to 1.

Gini Index

Considering a binary classification problem:

• \(1 - (0/100)^2 + (100/100)^2 = 0\) (pure)
• \(1 - (25/100)^2 + (75/100)^2 = 0.375\)
• \(1 - (50/100)^2 + (50/100)^2 = 0.5\)

Based on the above, are we solving a minimization or maximization problem?

When the problem is formulated as follows:

• For each candidate split \((k, t_k)\), compute

  \[ J(k,t_k) = \frac{m_{\text{left}}}{m} G_{\text{left}} + \frac{m_{\text{right}}}{m} G_{\text{right}}. \]

• The algorithm then chooses the split with the lowest \(J\), i.e. the split that yields the smallest weighted impurity.

Many textbooks describe this as maximizing impurity reduction (information gain), which is just

\[ \Delta G = G_{\text{parent}} - J(k,t_k). \]

Minimizing \(J\) and maximizing \(\Delta G\) are equivalent problems.

Gini Index

def gini_index(p):
    """Calculate the Gini index."""
    return 1 - (p**2 + (1 - p)**2)

# Probability values for class 1
p_values = np.linspace(0, 1, 100)

# Calculate Gini index for each probability
gini_values = [gini_index(p) for p in p_values]

# Plot the Gini index
plt.figure(figsize=(8, 6))
plt.plot(p_values, gini_values, label='Gini Index', color='b')
plt.title('Gini Index for Binary Classification')
plt.xlabel('Probability of Class 1 (p)')
plt.ylabel('Gini Index')
plt.grid(True)
plt.legend()
plt.show()

Iris Dataset

Attribution: (Géron 2019), Figures 6.1 and 6.2

Complete Example

Decision and Classification Trees, Clearly Explained!!!, (18 m 7s) StatQuest, 2021-04-26

Stopping Criteria

• All the examples in a given node belong to the same class.
• Depth of the tree would exceed max_depth.
• Number of examples in the node is min_sample_split or less.
• None of the splits decreases impurity sufficiently (min_impurity_decrease).
• See documentation for other criteria.

Limitations

• Possibly creates large trees
  • Challenge for interpretation
  • Overfitting
• Greedy algorithm, no guarantee to find the optimal tree. (Hyafil and Rivest 1976)
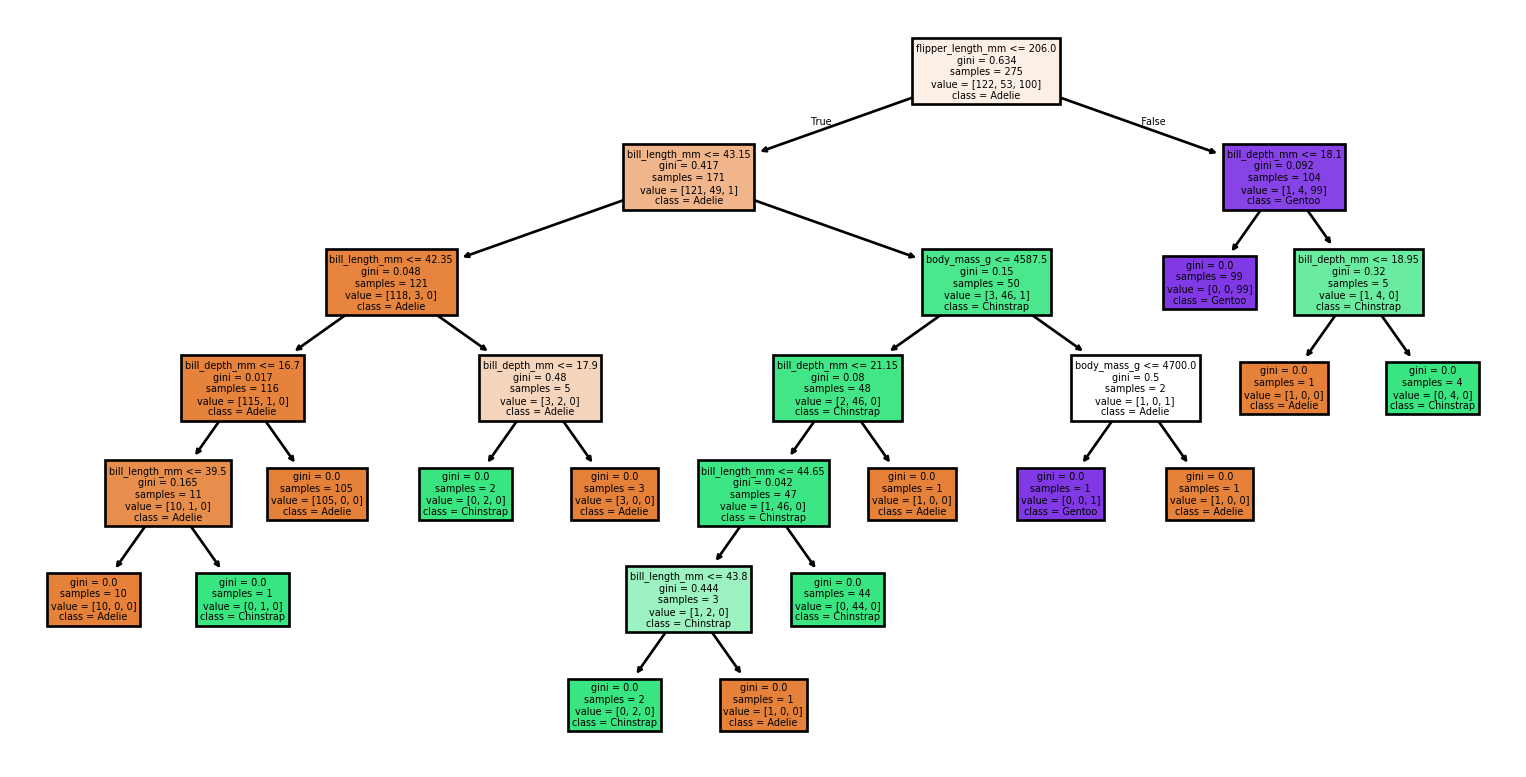
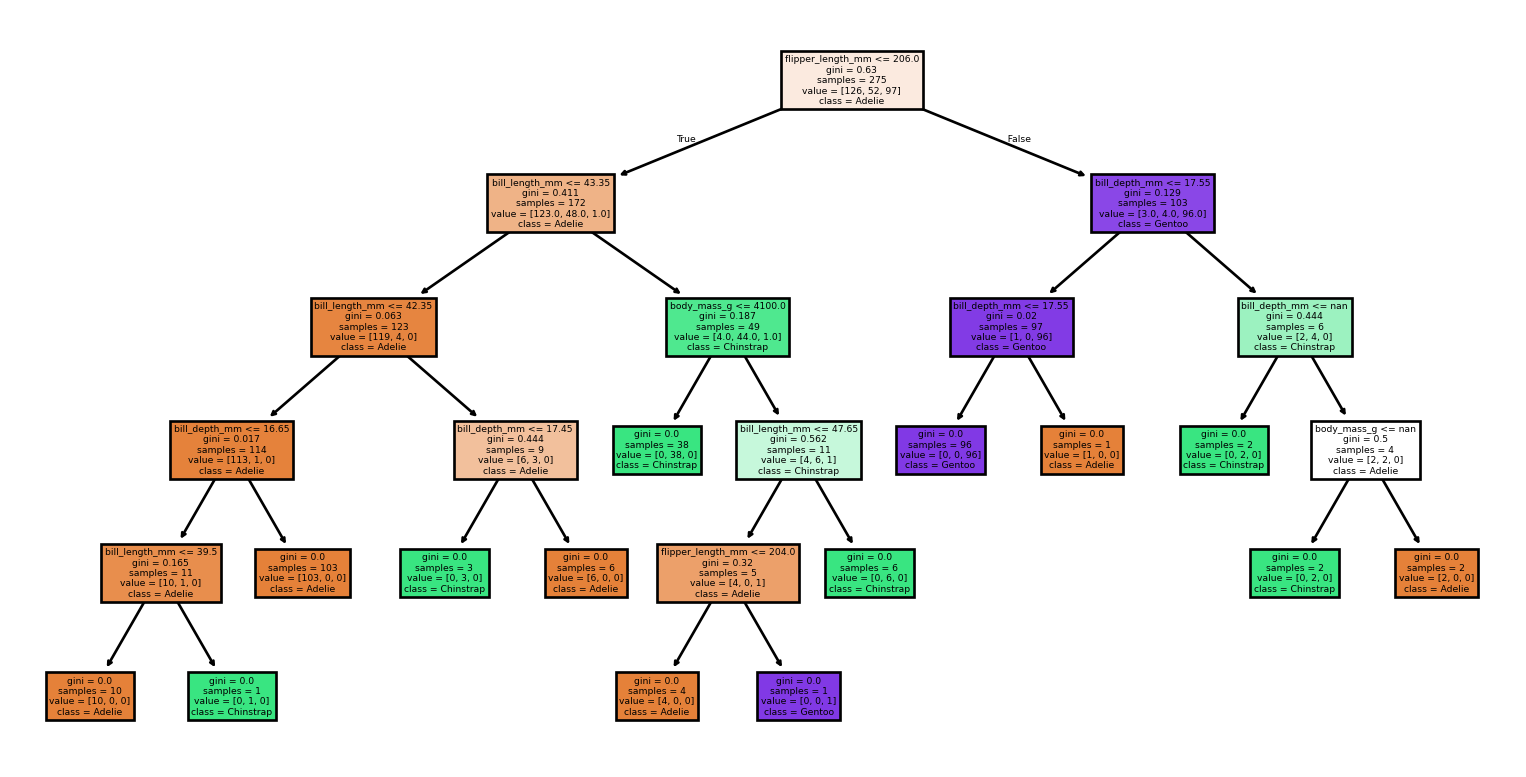
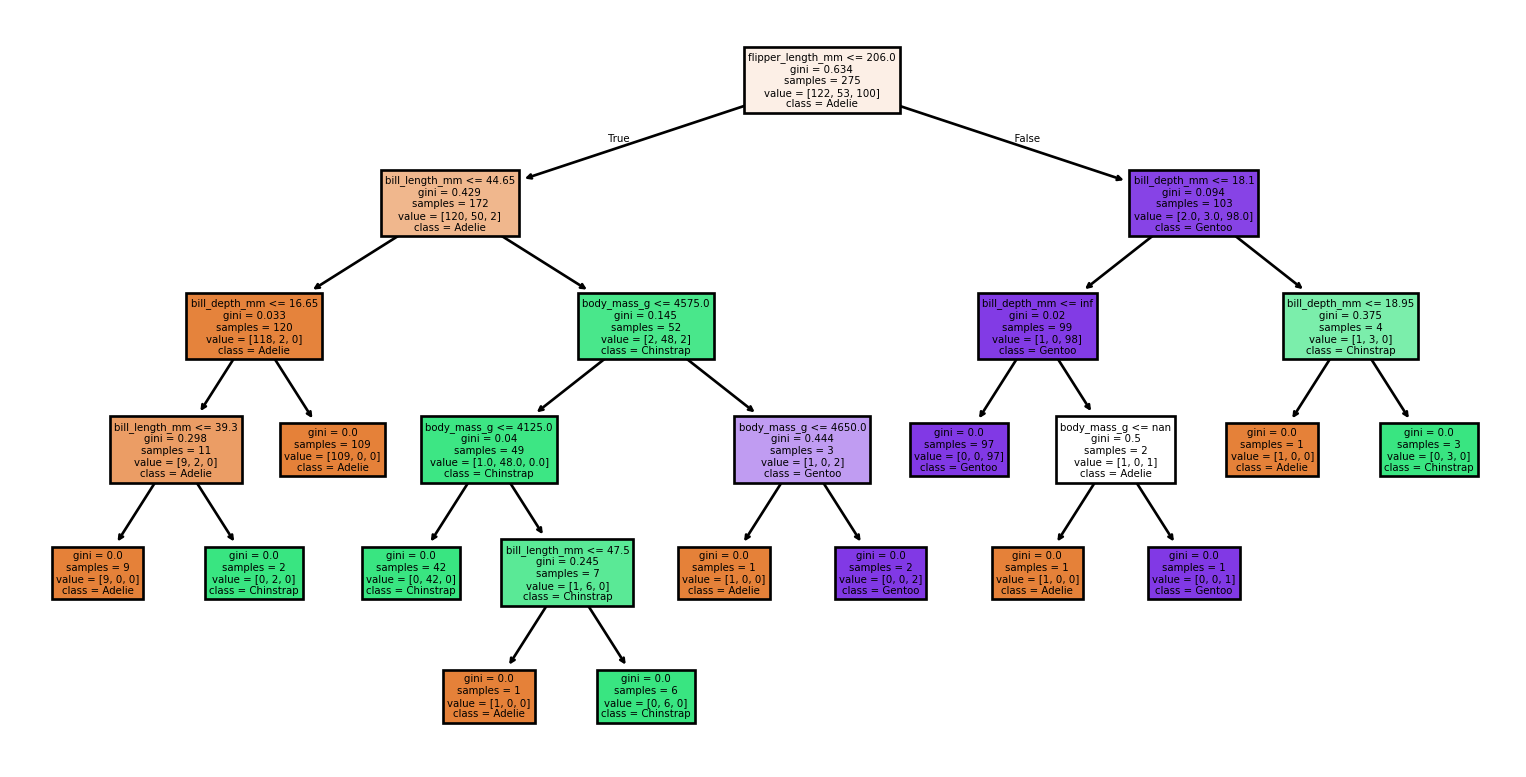
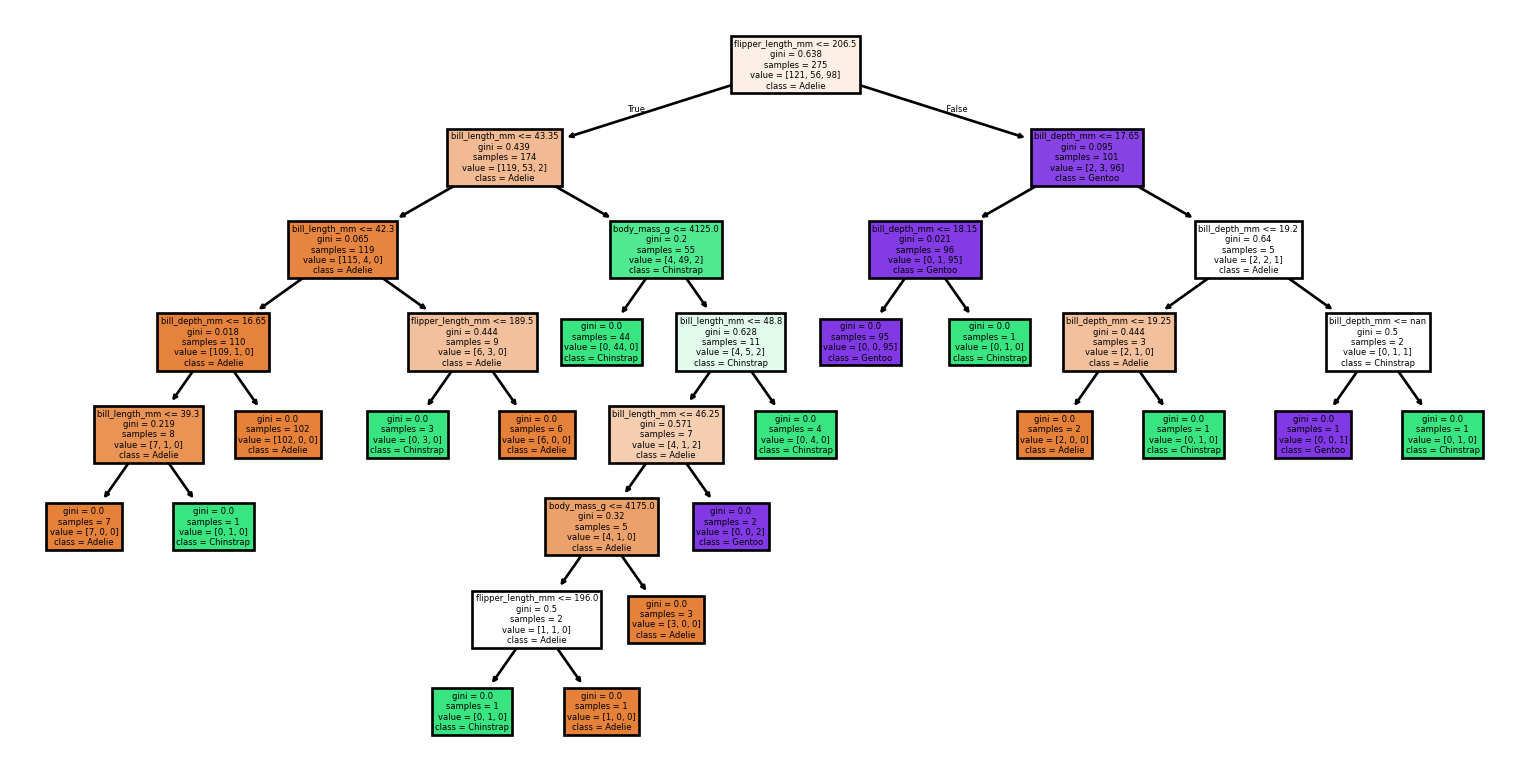
• Small changes to the data set produce vastly different trees

Large Trees

(Stiglic et al. 2012)

Small Changes to the Dataset

from sklearn import tree
from sklearn.metrics import classification_report, accuracy_score

# Loading the dataset

X, y = load_penguins(return_X_y = True)

target_names = ['Adelie','Chinstrap','Gentoo']

# Split the dataset into training and testing sets

for seed in (4, 7, 90, 96, 99, 2):

  print(f'Seed: {seed}')

  # Create new training and test sets based on a different random seed

  X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=seed)

  # Creating a new classifier

  clf = tree.DecisionTreeClassifier(random_state=seed)

  # Training

  clf.fit(X_train, y_train)

  # Make predictions

  y_pred = clf.predict(X_test)

  # Plotting the tree

  tree.plot_tree(clf, 
               feature_names = X.columns,
               class_names = target_names,
               filled = True)
  plt.show()

  # Evaluating the model

  accuracy = accuracy_score(y_test, y_pred)

  report = classification_report(y_test, y_pred, target_names=target_names)

  print(f'Accuracy: {accuracy:.2f}')
  print('Classification Report:')
  print(report)

Small Changes to the Dataset

Seed: 4

Accuracy: 0.99
Classification Report:
              precision    recall  f1-score   support

      Adelie       1.00      0.97      0.99        36
   Chinstrap       0.94      1.00      0.97        17
      Gentoo       1.00      1.00      1.00        16

    accuracy                           0.99        69
   macro avg       0.98      0.99      0.99        69
weighted avg       0.99      0.99      0.99        69

Seed: 7

Accuracy: 0.91
Classification Report:
              precision    recall  f1-score   support

      Adelie       0.96      0.83      0.89        30
   Chinstrap       0.83      1.00      0.91        15
      Gentoo       0.92      0.96      0.94        24

    accuracy                           0.91        69
   macro avg       0.90      0.93      0.91        69
weighted avg       0.92      0.91      0.91        69

Seed: 90

Accuracy: 0.94
Classification Report:
              precision    recall  f1-score   support

      Adelie       0.90      1.00      0.95        26
   Chinstrap       0.93      0.88      0.90        16
      Gentoo       1.00      0.93      0.96        27

    accuracy                           0.94        69
   macro avg       0.94      0.93      0.94        69
weighted avg       0.95      0.94      0.94        69

Seed: 96

Accuracy: 0.90
Classification Report:
              precision    recall  f1-score   support

      Adelie       0.83      0.97      0.89        30
   Chinstrap       1.00      0.67      0.80        15
      Gentoo       0.96      0.96      0.96        24

    accuracy                           0.90        69
   macro avg       0.93      0.86      0.88        69
weighted avg       0.91      0.90      0.90        69

Seed: 99

Accuracy: 1.00
Classification Report:
              precision    recall  f1-score   support

      Adelie       1.00      1.00      1.00        31
   Chinstrap       1.00      1.00      1.00        12
      Gentoo       1.00      1.00      1.00        26

    accuracy                           1.00        69
   macro avg       1.00      1.00      1.00        69
weighted avg       1.00      1.00      1.00        69

Seed: 2

Accuracy: 0.55
Classification Report:
              precision    recall  f1-score   support

      Adelie       0.62      0.97      0.75        30
   Chinstrap       0.43      0.90      0.58        10
      Gentoo       0.00      0.00      0.00        29

    accuracy                           0.55        69
   macro avg       0.35      0.62      0.44        69
weighted avg       0.33      0.55      0.41        69

Linear Regression

Supervised Learning - Regression

• The training data is a collection of labelled examples.
  • \(\{(x_i,y_i)\}_{i=1}^N\)
    • Each \(x_i\) is a feature vector with \(D\) dimensions.
    • \(x_i^{(j)}\) is the value of the feature \(j\) of the example \(i\), for \(j \in 1 \ldots D\) and \(i \in 1 \ldots N\).
  • The label \(y_i\) is a real number.
• Problem: Given the data set as input, create a model that can be used to predict the value of \(y\) for an unseen \(x\).

Can you think of examples of regression tasks?

. . .

1. House Price Prediction:
   • Application: Estimating the market value of residential properties based on features such as location, size, number of bedrooms, age, and amenities.
2. Stock Market Forecasting:
   • Application: Predicting future prices of stocks or indices based on historical data, financial indicators, and economic variables.
3. Weather Prediction:
   • Application: Estimating future temperatures, rainfall, and other weather conditions using historical weather data and atmospheric variables.
4. Sales Forecasting:
   • Application: Predicting future sales volumes for products or services by analyzing past sales data, market trends, and seasonal patterns.
5. Energy Consumption Prediction:
   • Application: Forecasting future energy usage for households, industries, or cities based on historical consumption data, weather conditions, and economic factors.
6. Medical Cost Estimation:
   • Application: Predicting healthcare costs for patients based on their medical history, demographic information, and treatment plans.
7. Traffic Flow Prediction:
   • Application: Estimating future traffic volumes and congestion levels on roads and highways using historical traffic data and real-time sensor inputs.
8. Customer Lifetime Value (CLV) Estimation:
   • Application: Predicting the total revenue a business can expect from a customer over the duration of their relationship, based on purchasing behavior and demographic data.
9. Economic Indicators Forecasting:
   • Application: Predicting key economic indicators such as GDP growth, unemployment rates, and inflation using historical economic data and market trends.
10. Demand Forecasting:
    • Application: Estimating future demand for products or services in various industries like retail, manufacturing, and logistics to optimize inventory and supply chain management.
11. Real Estate Valuation:
    • Application: Assessing the market value of commercial properties like office buildings, malls, and industrial spaces based on location, size, and market conditions.
12. Insurance Risk Assessment:
    • Application: Predicting the risk associated with insuring individuals or properties, which helps in determining premium rates, based on historical claims data, and demographic factors.
13. Ad Click-Through Rate (CTR) Prediction:
    • Application: Estimating the likelihood that a user will click on an online advertisement based on user behavior, ad characteristics, and contextual factors.
14. Loan Default Prediction:
    • Application: Predicting the probability of a borrower defaulting on a loan based on credit history, income, loan amount, and other financial indicators.

Focusing on applications possibly running on a mobile device.

1. Battery Life Prediction:
   • Application: Estimating remaining battery life based on usage patterns, running applications, and device settings.
2. Health and Fitness Tracking:
   • Application: Predicting calorie burn, heart rate, or sleep quality based on user activity, biometrics, and historical health data.
3. Personal Finance Management:
   • Application: Forecasting future expenses or savings based on spending habits, income patterns, and budget goals.
4. Weather Forecasting:
   • Application: Providing personalized weather forecasts based on current location and historical weather data.
5. Traffic and Commute Time Estimation:
   • Application: Predicting travel times and suggesting optimal routes based on historical traffic data, real-time conditions, and user behavior.
6. Image and Video Quality Enhancement:
   • Application: Adjusting image or video quality settings (e.g., brightness, contrast) based on lighting conditions and user preferences.
7. Fitness Goal Achievement:
   • Application: Estimating the time needed to achieve fitness goals such as weight loss or muscle gain based on user activity and dietary input.
8. Mobile Device Performance Optimization:
   • Application: Predicting the optimal settings for device performance and battery life based on usage patterns and app activity.

Rationale

Linear regression is introduced to conveniently present a well-known training algorithm, gradient descent. Additionally, it serves as a foundation for introducing logistic regression–a classification algorithm—which further facilitates discussions on artificial neural networks.

• Linear Regression
  • Gradient Descent
  • Logistic Regression
    • Neural Networks

The training algorithms for machine learning models can vary significantly depending on the model (e.g., decision trees, SVMs, etc.). In order to fit our schedule, we will concentrate on this specific sequence.

The concept of linear regression can be traced back to the early work of Sir Francis Galton in the late 19th century. Galton introduced the idea of “regression” in his 1886 paper, which focused on the relationship between the heights of parents and their children. He observed that children’s heights tended to regress towards the average, which led to the term “regression.”

However, the mathematical formulation of linear regression is closely associated with the work of Karl Pearson, who in the early 20th century extended Galton’s ideas to create the method of least squares for fitting a linear model. The method itself, though, was developed earlier in 1805 by Adrien-Marie Legendre and independently by Carl Friedrich Gauss for astronomical data analysis.

See: Stanton (2001).

Linear Regression

A linear model assumes that the value of the label, \(\hat{y_i}\), can be expressed as a linear combination of the feature values, \(x_i^{(j)}\): \[ \hat{y_i} = \theta_0 + \theta_1 x_i^{(1)} + \theta_2 x_i^{(2)} + \ldots + \theta_D x_i^{(D)} \]

Here, \(\theta_{j}\) is the \(j\)th parameter of the (linear) model, with \(\theta_0\) being the bias term/parameter, and \(\theta_1 \ldots \theta_D\) being the feature weights.

In statistical contexts, the notation \(\hat{y_i}\) is employed to denote the estimator of the true value \(y_i\). This represents the predicted or estimated outcome based on a given model.

Conversely, in machine learning, the notation \(h(x_i)\) is used, where \(h\) represents the hypothesis function or model applied to the input data \(x_i\). The hypothesis function \(h\) is derived from a predefined hypothesis space, which encompasses the set of all possible models that can be used to map input data to predicted outcomes.

The parameter \(\theta_0\) is called the bias term (also “intercept”) because:

• It shifts the prediction independently of the inputs.
• Geometrically, it moves the regression hyperplane up or down (or left/right in classification), so the model is not forced to pass through the origin.
• In machine learning terms, it acts like a constant offset, compensating for systematic effects not explained by the features.

So it’s called “bias” because it introduces a fixed baseline to which the contributions of the other parameters are added.

In my presentations, I use \(\hat{y_i}\) and \(h(x_i)\) synonymously.

Definition

Problem: find values for all the model parameters so that the model “best fits” the training data.

• The Root Mean Square Error is a common performance measure for regression problems.

\[ \sqrt{\frac{1}{N}\sum_1^N [h(x_i) - y_i]^2} \]

Minimizing RMSE

Attribution: Krishnavedala, CC BY-SA 3.0, via Wikimedia Commons

Characteristics

A typical learning algorithm comprises the following components:

1. A model, often consisting of a set of weights whose values will be “learnt”.
2. An objective function.
   • In the case of regression, this is often a loss function, a function that quantifies misclassification. The Root Mean Square Error is a common loss function for regression problems. \(\sqrt{\frac{1}{N}\sum_1^N [h(x_i) - y_i]^2}\)
3. Optimization algorithm

Optimization

Until some termination criteria is met¹:

• Evaluate the loss function, comparing \(h(x_i)\) to \(y_i\).
• Make small changes to the weights, in a way that reduces the value of the loss function.

1. E.g. the value of the loss function no longer decreases or the maximum number of iterations.

Remarks

• It is crucial to separate the optimization algorithm from the problem it addresses.
• For linear regression, an exact analytical solution exists, but it presents certain limitations.
• Gradient descent serves as a general algorithm applicable not only to linear regression, but also to logistic regression, deep learning, t-SNE (t-distributed Stochastic Neighbor Embedding), among various other problems.
• There exists a diverse range of optimization algorithms that do not rely on gradient-based methods.

Summary

• The lecture surveyed three learning algorithms, k-nearest neighbours (KNN), decision trees, and linear regression, and framed them via model, objective, and optimization.
• We then constructed decision trees, showed that regression leaves returned the sample mean, minimized the weighted impurity \(J\), and analyzed the Gini index.
• Decision boundaries were illustrated for linear and non-linear models.
• Finally, we formulated linear regression with a bias term.

Prologue

References

Géron, Aurélien. 2019. Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow. 2nd ed. O’Reilly Media.

Geurts, Pierre, Alexandre Irrthum, and Louis Wehenkel. 2009. “Supervised Learning with Decision Tree-Based Methods in Computational and Systems Biology.” Molecular bioSystems 5 (12): 1593–1605. https://doi.org/10.1039/b907946g.

Hyafil, Laurent, and Ronald L. Rivest. 1976. “Constructing Optimal Binary Decision Trees Is NP-Complete.” Inf. Process. Lett. 5 (1): 15–17. https://doi.org/10.1016/0020-0190(76)90095-8.

Russell, Stuart, and Peter Norvig. 2020. Artificial Intelligence: A Modern Approach. 4th ed. Pearson. http://aima.cs.berkeley.edu/.

Stanton, Jeffrey M. 2001. “Galton, Pearson, and the Peas: A Brief History of Linear Regression for Statistics Instructors.” Journal of Statistics Education 9 (3). https://doi.org/10.1080/10691898.2001.11910537.

Stiglic, Gregor, Simon Kocbek, Igor Pernek, and Peter Kokol. 2012. “Comprehensive Decision Tree Models in Bioinformatics.” Edited by Ahmed Moustafa. PLoS ONE 7 (3): e33812. https://doi.org/10.1371/journal.pone.0033812.

Next lecture

• Training a linear model

Marcel Turcotte

Marcel.Turcotte@uOttawa.ca

School of Electrical Engineering and Computer Science (EECS)

University of Ottawa