import pandas as pd
WOLFRAM_CSV = "https://raw.githubusercontent.com/turcotte/csi4106-f25/refs/heads/main/datasets/old_faithful_eruptions/Sample-Data-Old-Faithful-Eruptions.csv"
df = pd.read_csv(WOLFRAM_CSV)
# Renaming the columns
df = df.rename(columns={"Duration": "eruptions", "WaitingTime": "waiting"})
print(df.shape)
df.head(6)Linear regression and gradient descent
CSI 4106 - Fall 2025
Version: Sep 16, 2025 17:58
Preamble
Message of the Day
Learning Objectives
- Differentiate regression tasks from classification tasks.
- Articulate the training methodology for linear regression models.
- Interpret the function of optimization algorithms in addressing linear regression.
- Detail the significance of partial derivatives within the gradient descent algorithm.
- Contrast the batch, stochastic, and mini-batch gradient descent methods.
Linear Regression
Rationale
Linear regression is introduced to conveniently present a well-known training algorithm, gradient descent. Additionally, it serves as a foundation for introducing logistic regression–a classification algorithm—which further facilitates discussions on artificial neural networks.
- Linear Regression
- Gradient Descent
- Logistic Regression
- Neural Networks
Supervised Learning - Regression
- The training data is a collection of labelled examples.
- \(\{(x_i,y_i)\}_{i=1}^N\)
- Each \(x_i\) is a feature vector with \(D\) dimensions.
- \(x_i^{(j)}\) is the value of the feature \(j\) of the example \(i\), for \(j \in 1 \ldots D\) and \(i \in 1 \ldots N\).
- The label \(y_i\) is a real number.
- \(\{(x_i,y_i)\}_{i=1}^N\)
- Problem: Given the data set as input, create a model that can be used to predict the value of \(y\) for an unseen \(x\).
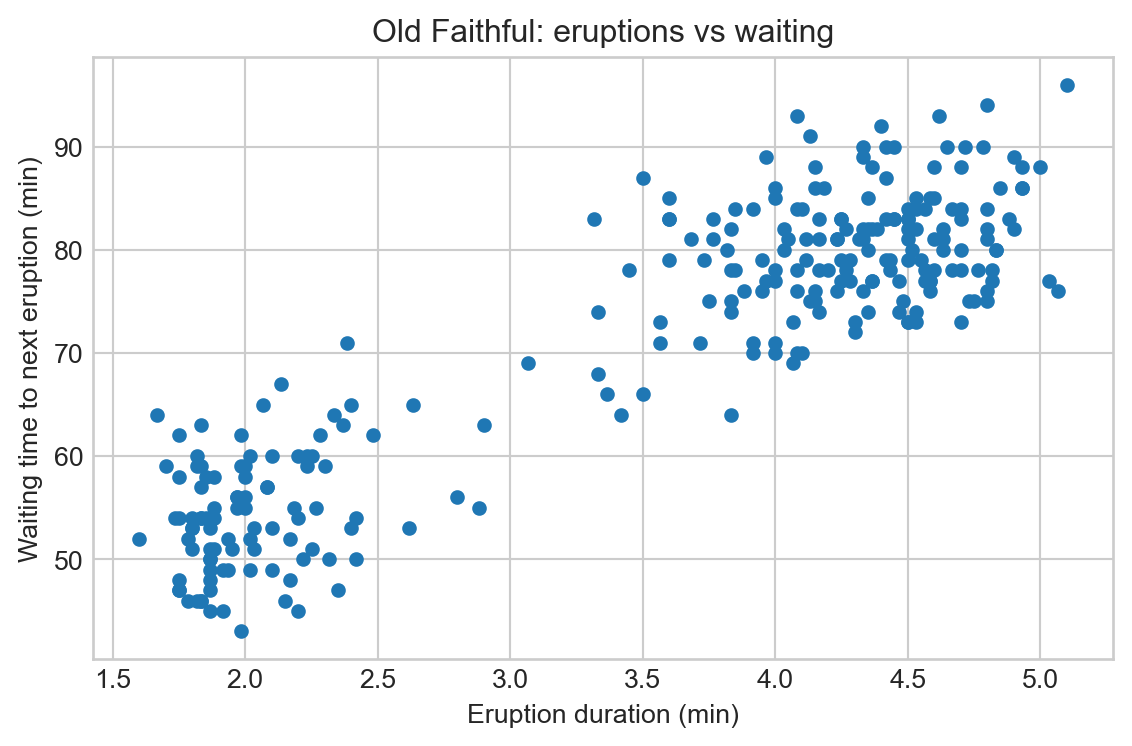
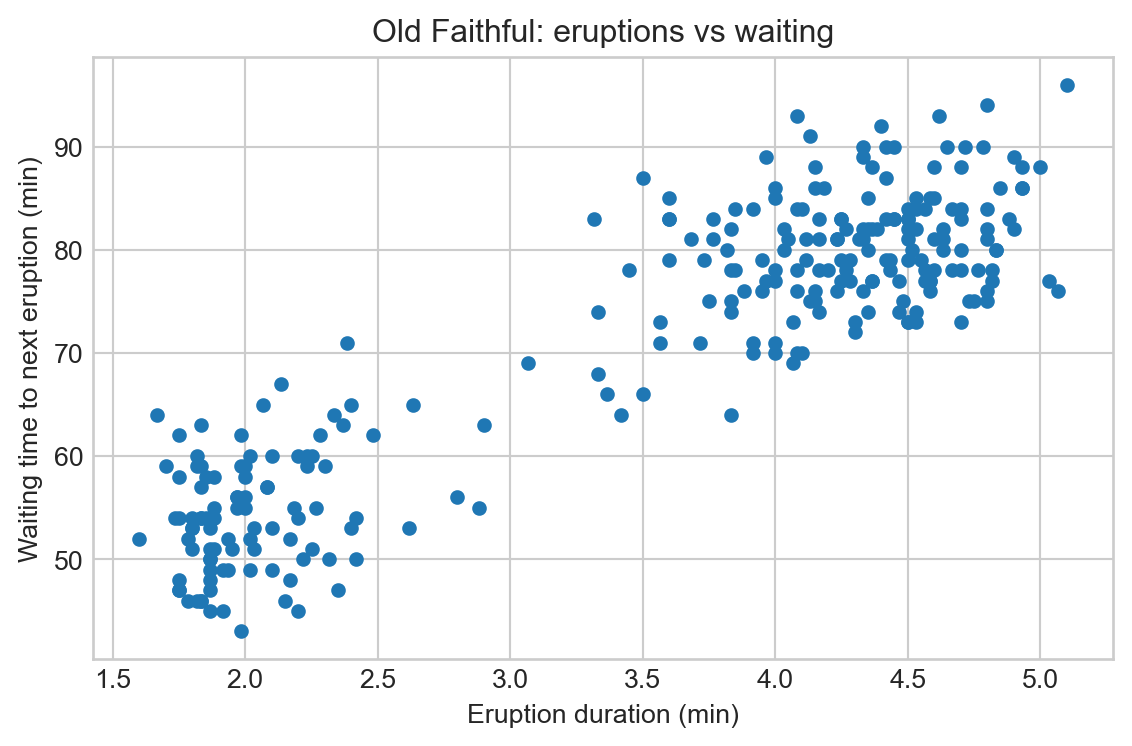
Old Faithful Eruptions
Old Faithful Eruptions
(272, 2)| eruptions | waiting | |
|---|---|---|
| 0 | 3.600 | 79 |
| 1 | 1.800 | 54 |
| 2 | 3.333 | 74 |
| 3 | 2.283 | 62 |
| 4 | 4.533 | 85 |
| 5 | 2.883 | 55 |
Old Faithful Geyser
Quick Visualization
Problem
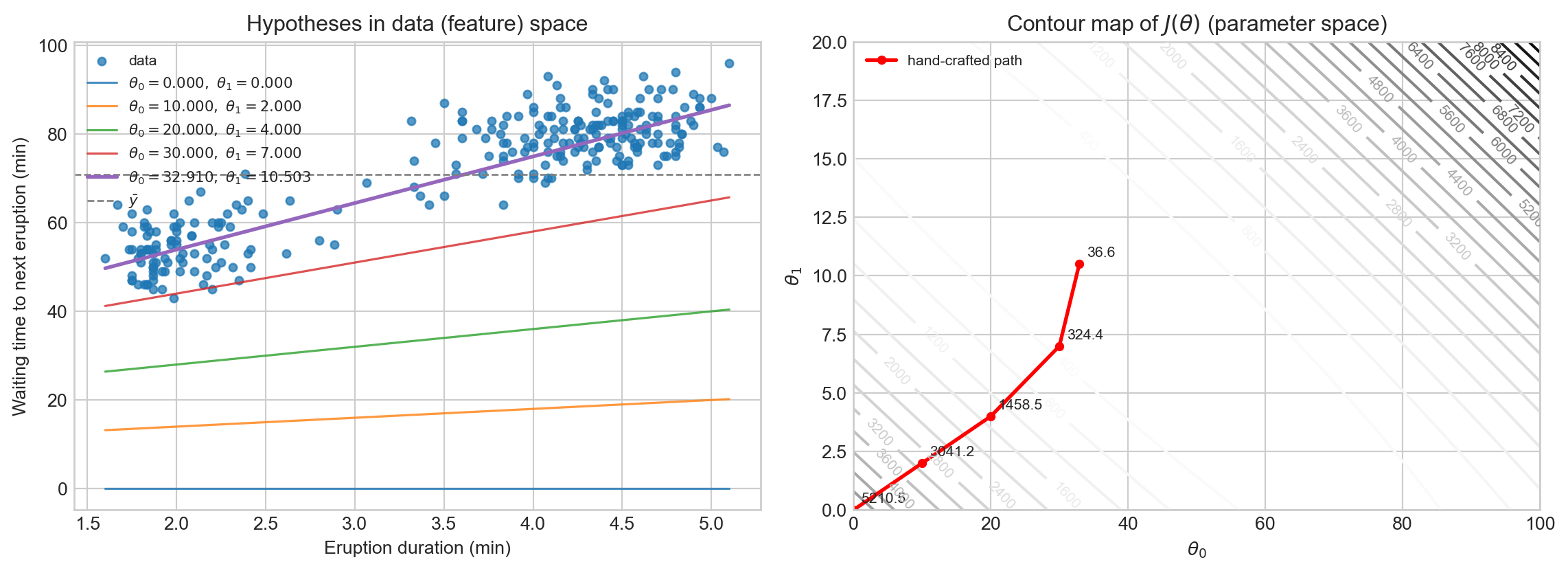
- Predict the waiting time until the next eruption (min), \(y\), based on the duration of the current eruption (min), \(x\).
Linear Regression
A linear model assumes that the value of the label, \(\hat{y_i}\), can be expressed as a linear combination of the feature values, \(x_i^{(j)}\): \[ \hat{y_i} = \theta_0 + \theta_1 x_i^{(1)} + \theta_2 x_i^{(2)} + \ldots + \theta_D x_i^{(D)} \]
Here, \(\theta_{j}\) is the \(j\)th parameter of the (linear) model, with \(\theta_0\) being the bias term/parameter, and \(\theta_1 \ldots \theta_D\) being the feature weights.
Definition
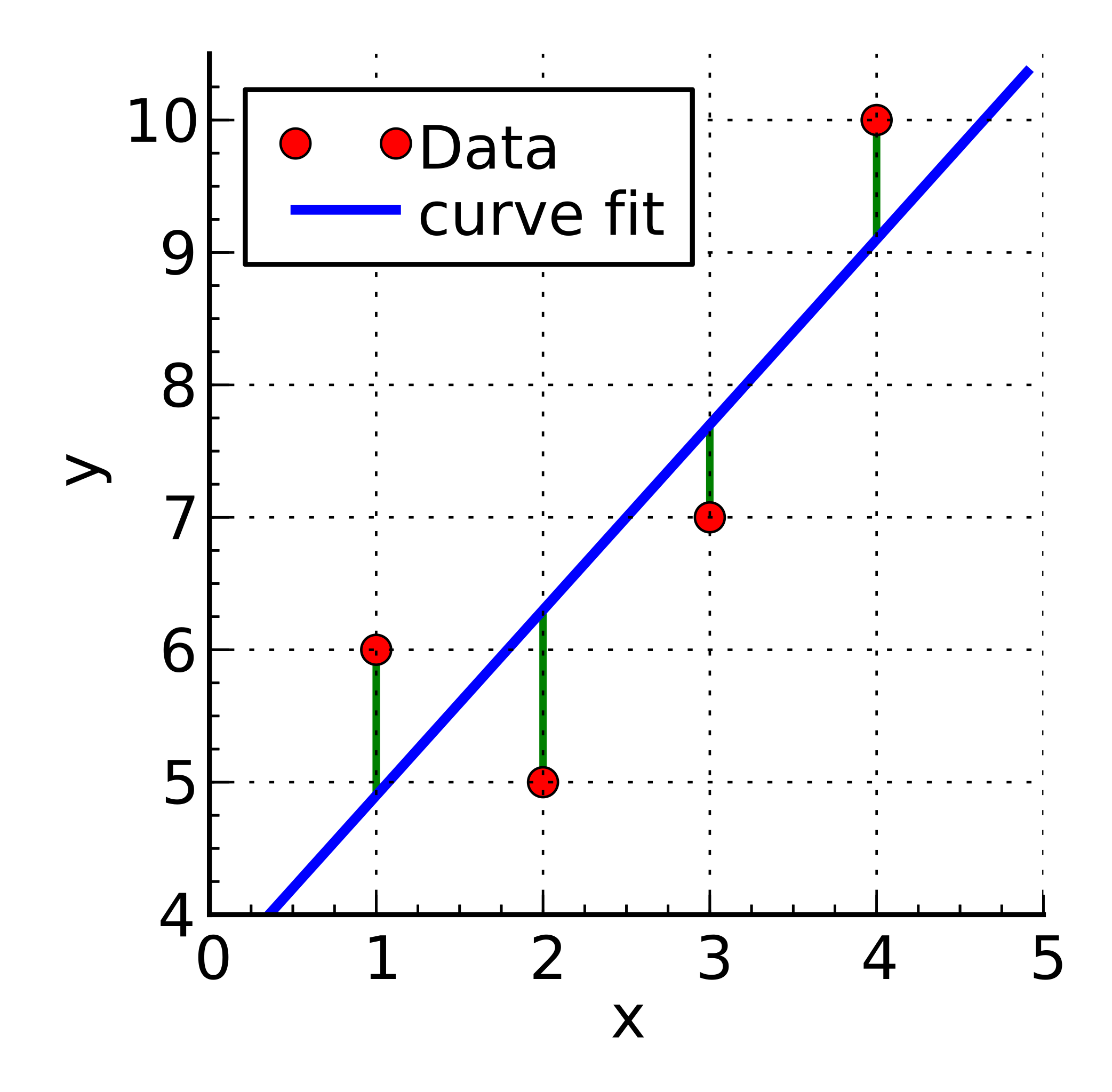
Problem: find values for all the model parameters so that the model “best fits” the training data.
- The Root Mean Square Error is a common performance measure for regression problems.
\[ \sqrt{\frac{1}{N}\sum_1^N [h(x_i) - y_i]^2} \]
Minimizing RMSE
Learning
Code
from sklearn.linear_model import SGDRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
# Prepare data
X = df[["eruptions"]].values # shape (n_samples, 1)
y = df["waiting"].values # shape (n_samples,)
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=42
)
# Fit via SGDRegressor — linear model via gradient descent
sgd = SGDRegressor(
loss="squared_error",
penalty=None,
learning_rate="constant",
eta0=0.01,
max_iter=2000,
tol=None,
random_state=42
)
sgd.fit(X_train, y_train)
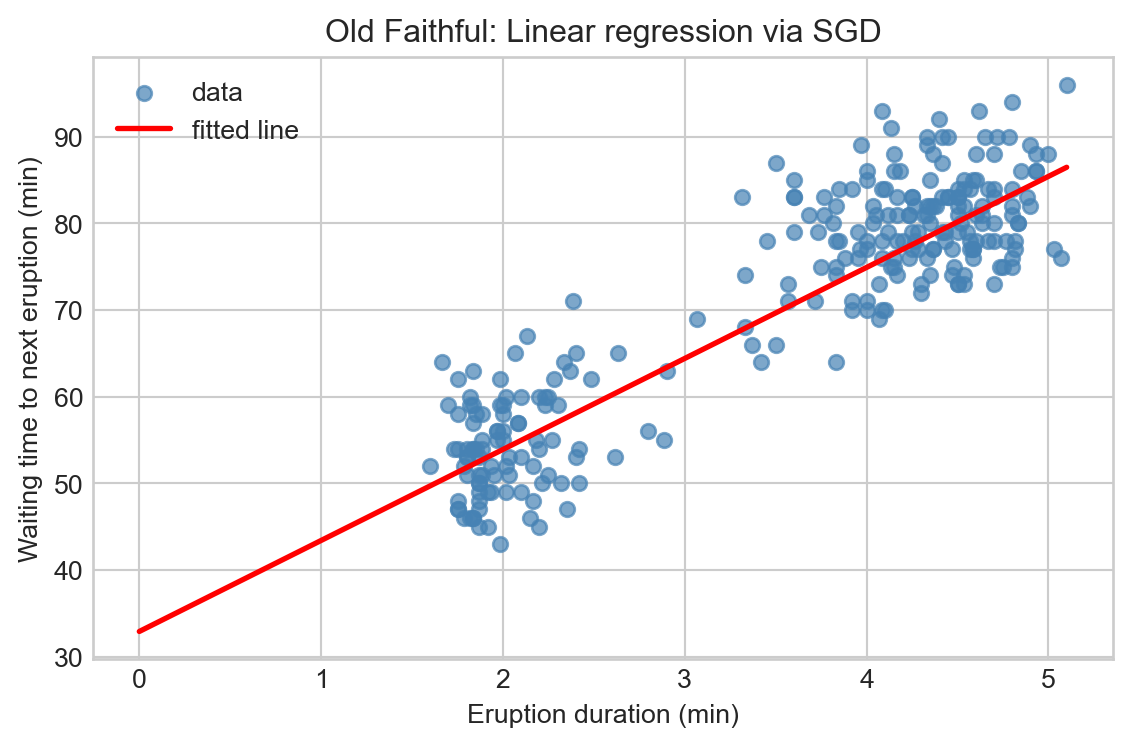
print("Learned parameters:")
print(f" intercept = {sgd.intercept_[0]:.3f}")
print(f" slope = {sgd.coef_[0]:.3f}")
y_pred = sgd.predict(X_test)
print(f"Test MSE = {mean_squared_error(y_test, y_pred):.2f}")
print(f"Test R² = {r2_score(y_test, y_pred):.3f}")Learned parameters:
intercept = 32.910
slope = 10.503
Test MSE = 43.02
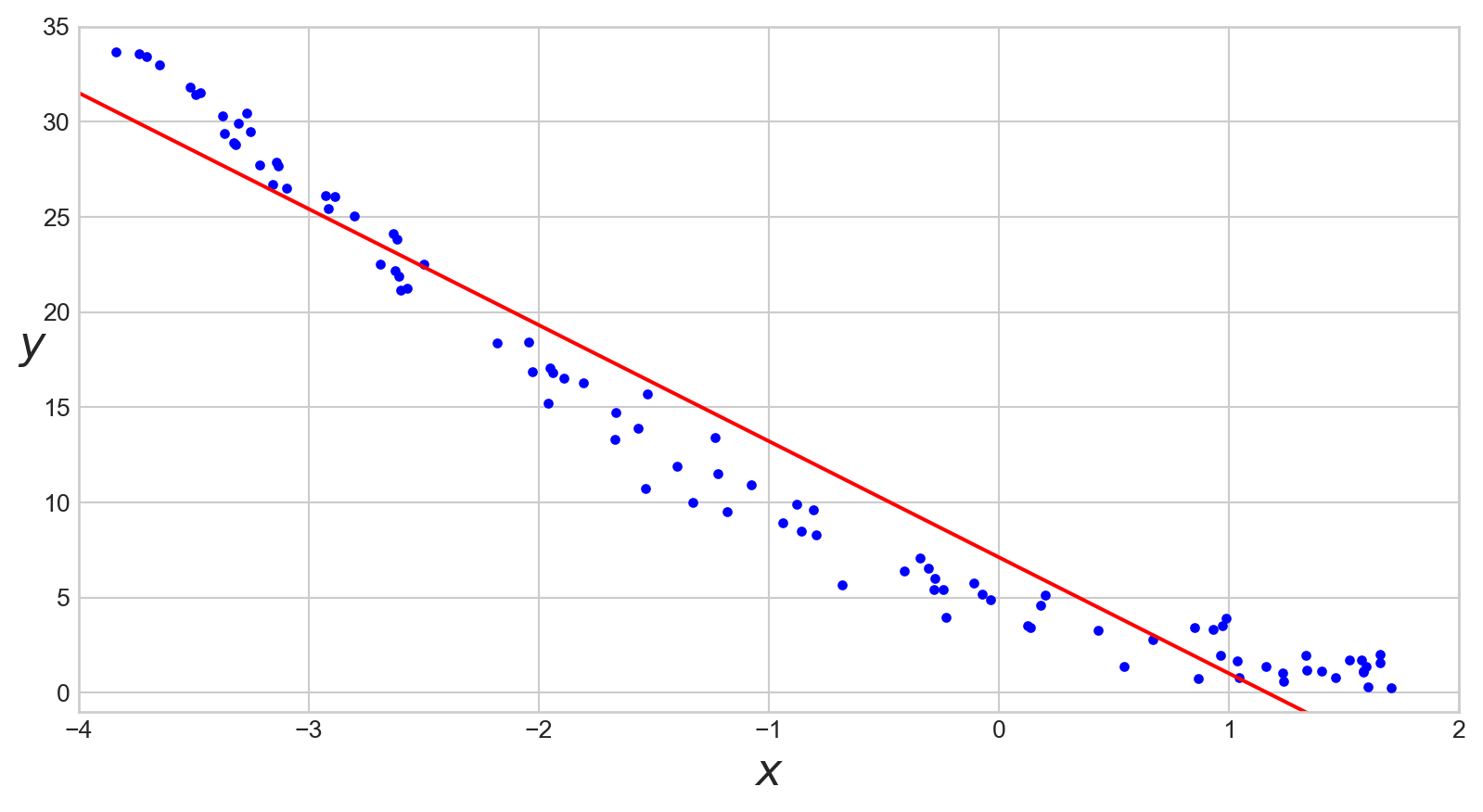
Test R² = 0.671Visualization
Code
import numpy as np
# Scatter the data
plt.figure(figsize=(6,4))
plt.scatter(X, y, color="steelblue", s=30, alpha=0.7, label="data")
# Plot the fitted line
x_line = np.linspace(0, X.max(), 100).reshape(-1, 1)
y_line = sgd.predict(x_line)
plt.plot(x_line, y_line, color="red", linewidth=2, label="fitted line")
plt.xlabel("Eruption duration (min)")
plt.ylabel("Waiting time to next eruption (min)")
plt.title("Old Faithful: Linear regression via SGD")
plt.legend()
plt.tight_layout()
plt.show()Characteristics
A typical learning algorithm comprises the following components:
- A model, often consisting of a set of parameters whose values will be “learnt”.
- An objective function.
- In the case of regression, this is often a loss function, a function that quantifies misclassification. The Root Mean Square Error is a common loss function for regression problems. \[ \sqrt{\frac{1}{N}\sum_1^N [h(x_i) - y_i]^2} \]
- Optimization algorithm
Optimization
Until some termination criteria is met1:
- Evaluate the loss function, comparing \(h(x_i)\) to \(y_i\).
- Make small changes to the parameters, in a way that reduces the value of the loss function.
Remarks
- It is important to separate the optimization algorithm from the problem it addresses.
- For linear regression, an exact analytical solution exists, but it presents certain limitations.
- Gradient descent serves as a general algorithm applicable not only to linear regression, but also to logistic regression, deep learning, t-SNE (t-distributed Stochastic Neighbor Embedding), among various other problems.
- There exists a diverse range of optimization algorithms that do not rely on gradient-based methods.
Optimization — single feature
Model (hypothesis):
\[ h(x_i; \theta) = \theta_0 + \theta_1 x_i^{(1)} \]Loss/cost function:
\[ J(\theta_0, \theta_1) = \frac{1}{N}\sum_{i=1}^N [h(x_i;\theta) - y_i]^2 \]
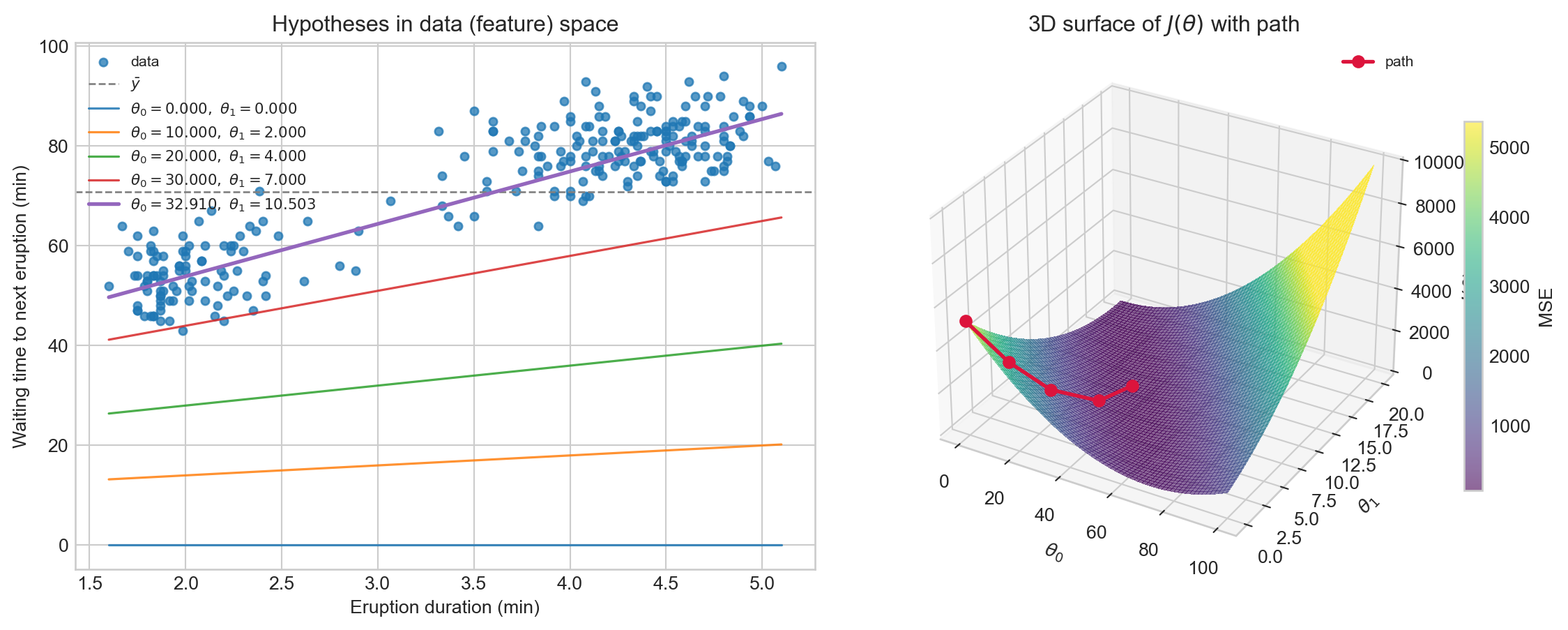
Hypothesis vs Parameter Space
Hypothesis vs Parameter Space
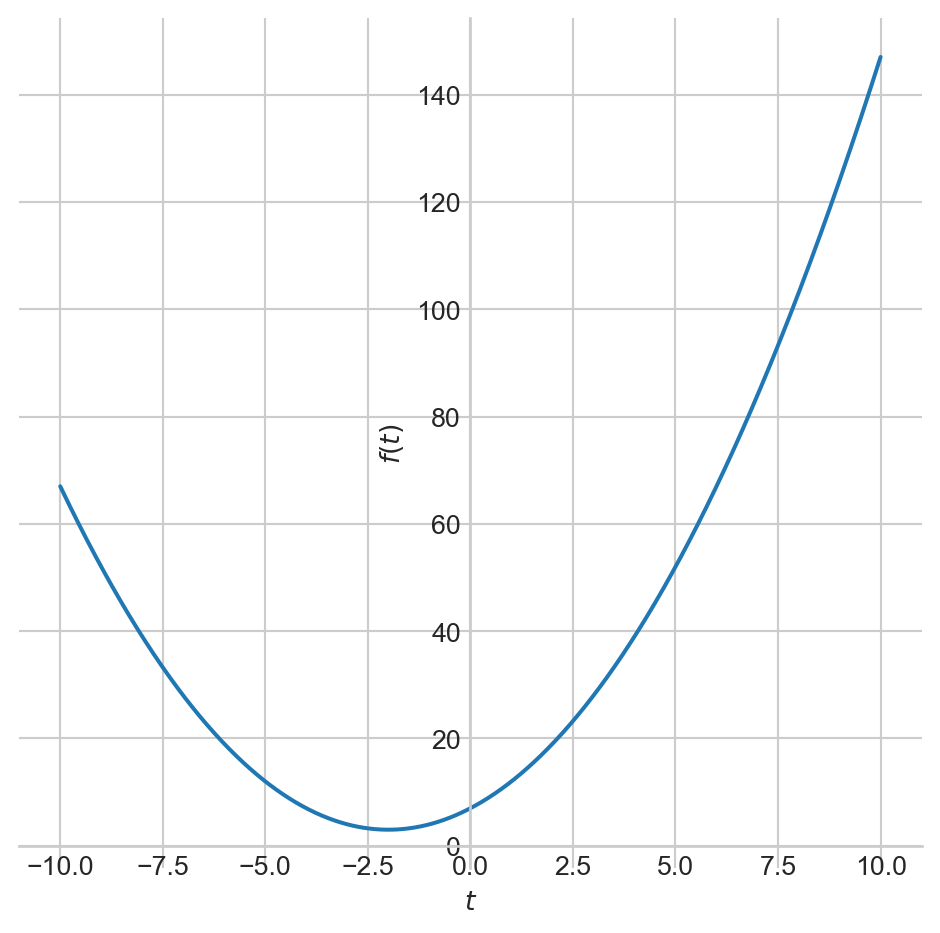
Derivative
Derivative
Source code
Derivative
Derivative
Derivative
Derivative
Source code
import sympy as sp
import numpy as np
import matplotlib.pyplot as plt
# Define the variable and function
t = sp.symbols('t')
f = t**2 + 4*t + 7
# Compute the derivative
f_prime = sp.diff(f, t)
# Lambdify the functions for numerical plotting
f_func = sp.lambdify(t, f, "numpy")
f_prime_func = sp.lambdify(t, f_prime, "numpy")
# Generate t values for plotting
t_vals = np.linspace(-5, 2, 400)
# Get y values for the function and its derivative
f_vals = f_func(t_vals)
f_prime_vals = f_prime_func(t_vals)
# Plot the function and its derivative
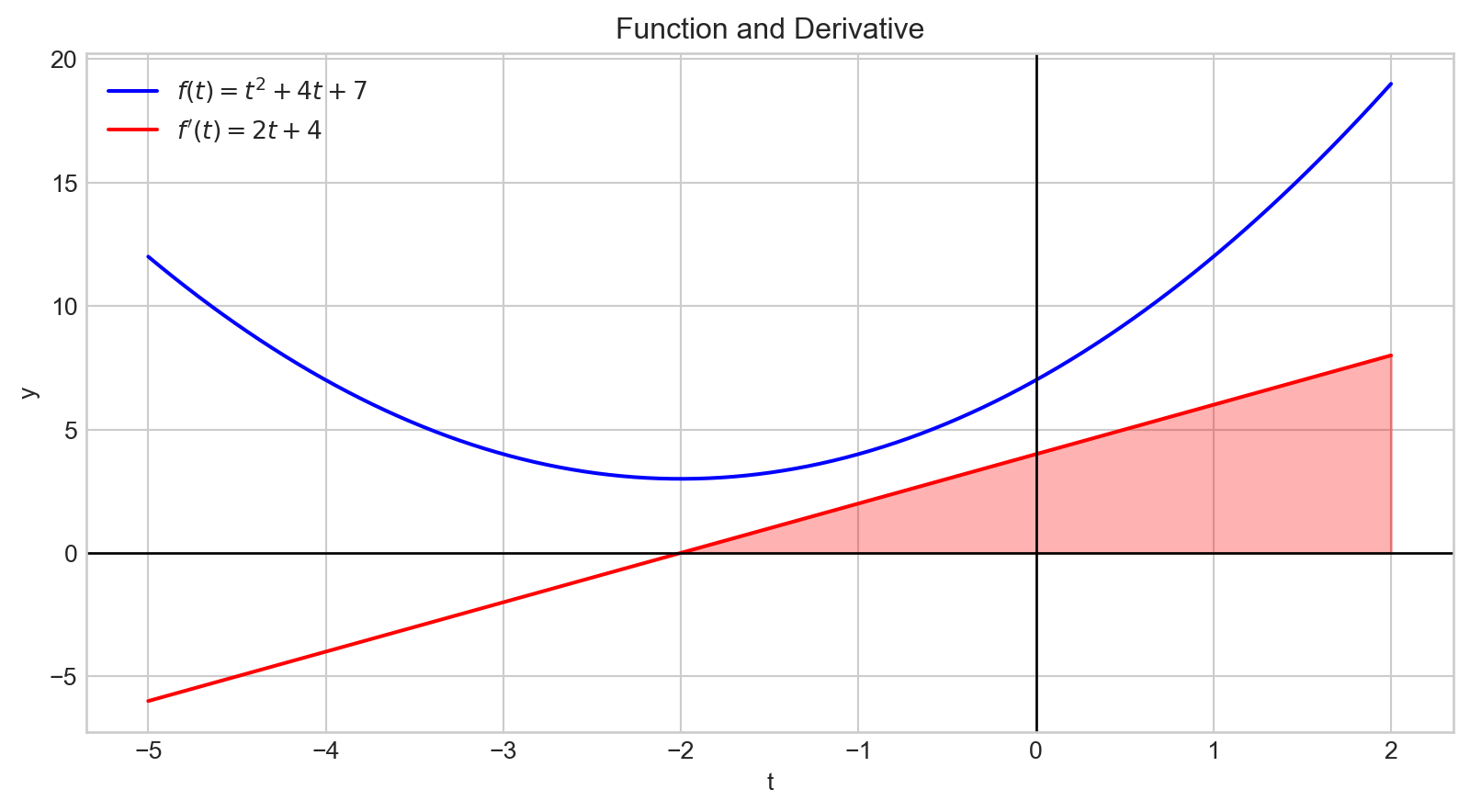
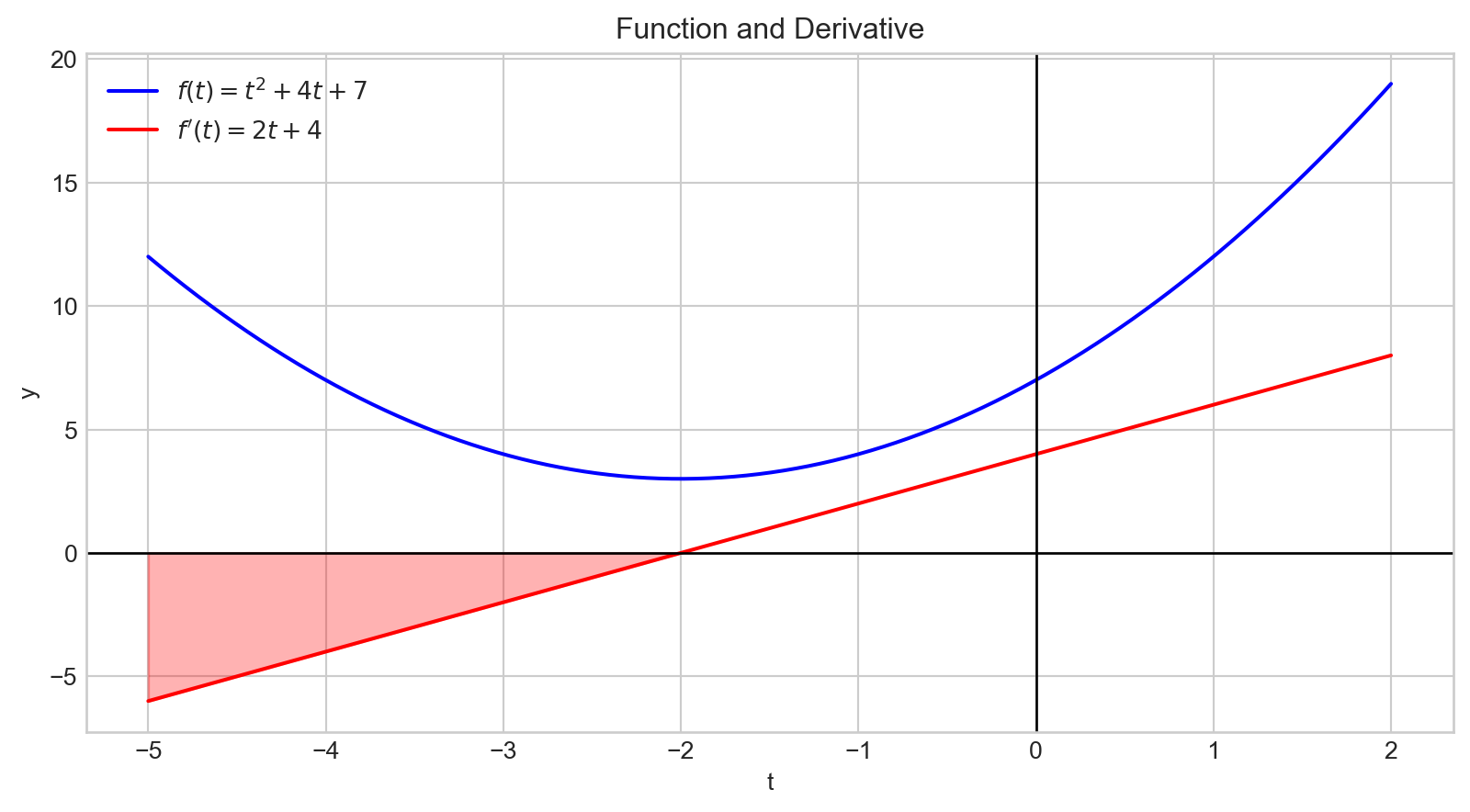
plt.plot(t_vals, f_vals, label=r'$f(t) = t^2 + 4t + 7$', color='blue')
plt.plot(t_vals, f_prime_vals, label=r"$f'(t) = 2t + 4$", color='red')
# Fill the area below the derivative where it's negative
plt.fill_between(t_vals, f_prime_vals, where=(f_prime_vals > 0), color='red', alpha=0.3)
# Add labels and legend
plt.axhline(0, color='black',linewidth=1)
plt.axvline(0, color='black',linewidth=1)
plt.title('Function and Derivative')
plt.xlabel('t')
plt.ylabel('y')
plt.legend()
# Show the plot
plt.grid(True)
plt.show()Gradient Descent
Gradient Descent — Single Feature
Model (hypothesis):
\[ h(x_i; \theta) = \theta_0 + \theta_1 x_i^{(1)} \]Loss/cost function:
\[ J(\theta_0, \theta_1) = \frac{1}{N}\sum_{i=1}^N [h(x_i;\theta) - y_i]^2 \]
Gradient descent - intuition
Gradient Descent - Step-by-Step
Gradient descent - single value
- Initialization: \(\theta_0\) and \(\theta_1\) - either with random values or zeros.
- Loop:
- repeat until convergence: \[ \theta_j := \theta_j - \alpha \frac {\partial}{\partial \theta_j}J(\theta_0, \theta_1) , \text{for } j=0 \text{ and } j=1 \]
- \(\alpha\) is called the learning rate - this is the size of each step.
- \(\frac {\partial}{\partial \theta_j}J(\theta_0, \theta_1)\) is the partial derivative with respect to \(\theta_j\).
Gradient Descent - Single Value
Code
import sympy as sp
import numpy as np
import matplotlib.pyplot as plt
# Define the variable and function
t = sp.symbols('t')
f = t**2 + 4*t + 7
# Compute the derivative
f_prime = sp.diff(f, t)
# Lambdify the functions for numerical plotting
f_func = sp.lambdify(t, f, "numpy")
f_prime_func = sp.lambdify(t, f_prime, "numpy")
# Generate t values for plotting
t_vals = np.linspace(-5, 2, 400)
# Get y values for the function and its derivative
f_vals = f_func(t_vals)
f_prime_vals = f_prime_func(t_vals)
# Plot the function and its derivative
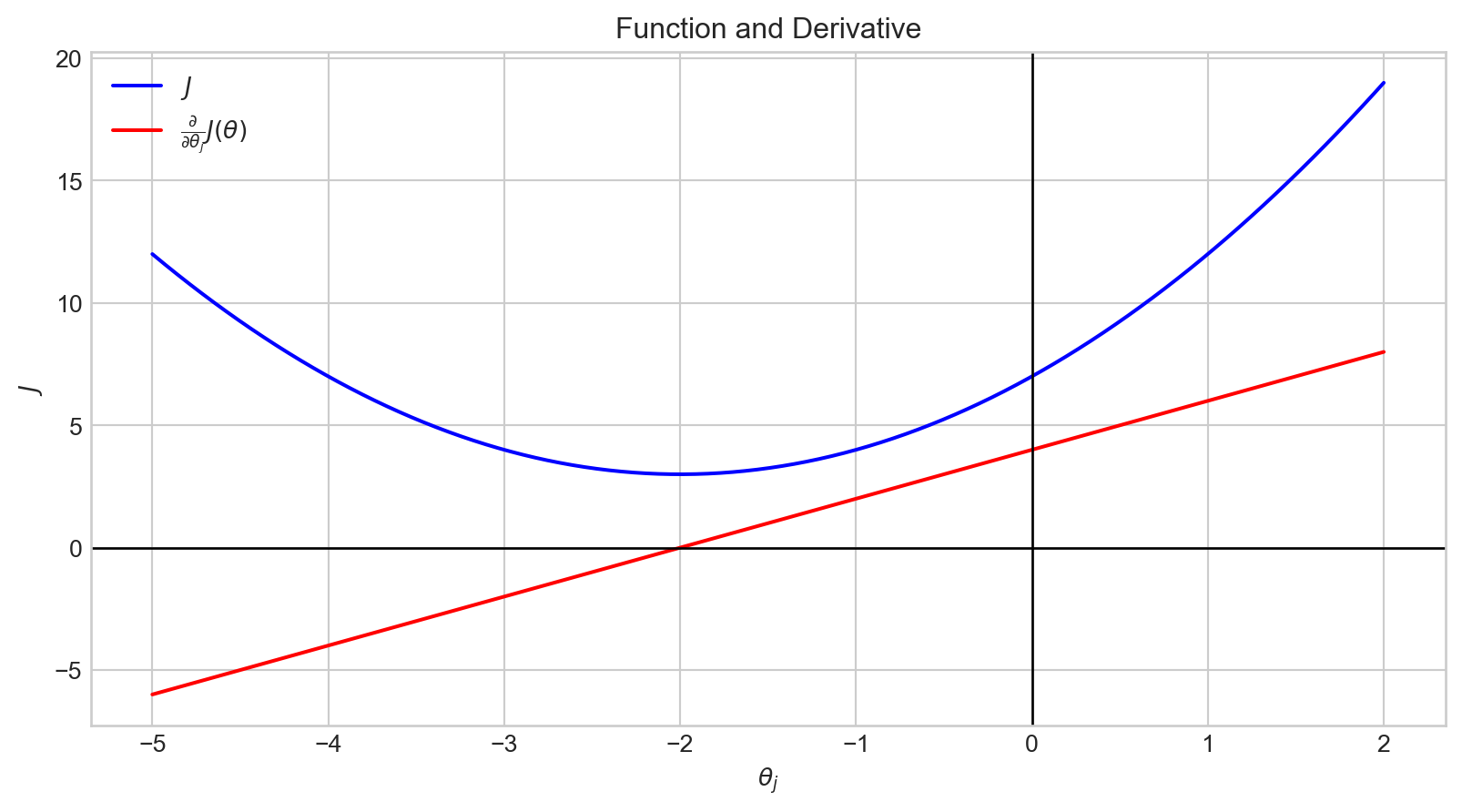
plt.plot(t_vals, f_vals, label=r'$J$', color='blue')
plt.plot(t_vals, f_prime_vals, label=r"$\frac {\partial}{\partial \theta_j}J(\theta)$", color='red')
# Add labels and legend
plt.axhline(0, color='black',linewidth=1)
plt.axvline(0, color='black',linewidth=1)
plt.title('Function and Derivative')
plt.xlabel(r'$\theta_j$')
plt.ylabel(r'$J$')
plt.legend()
# Show the plot
plt.grid(True)
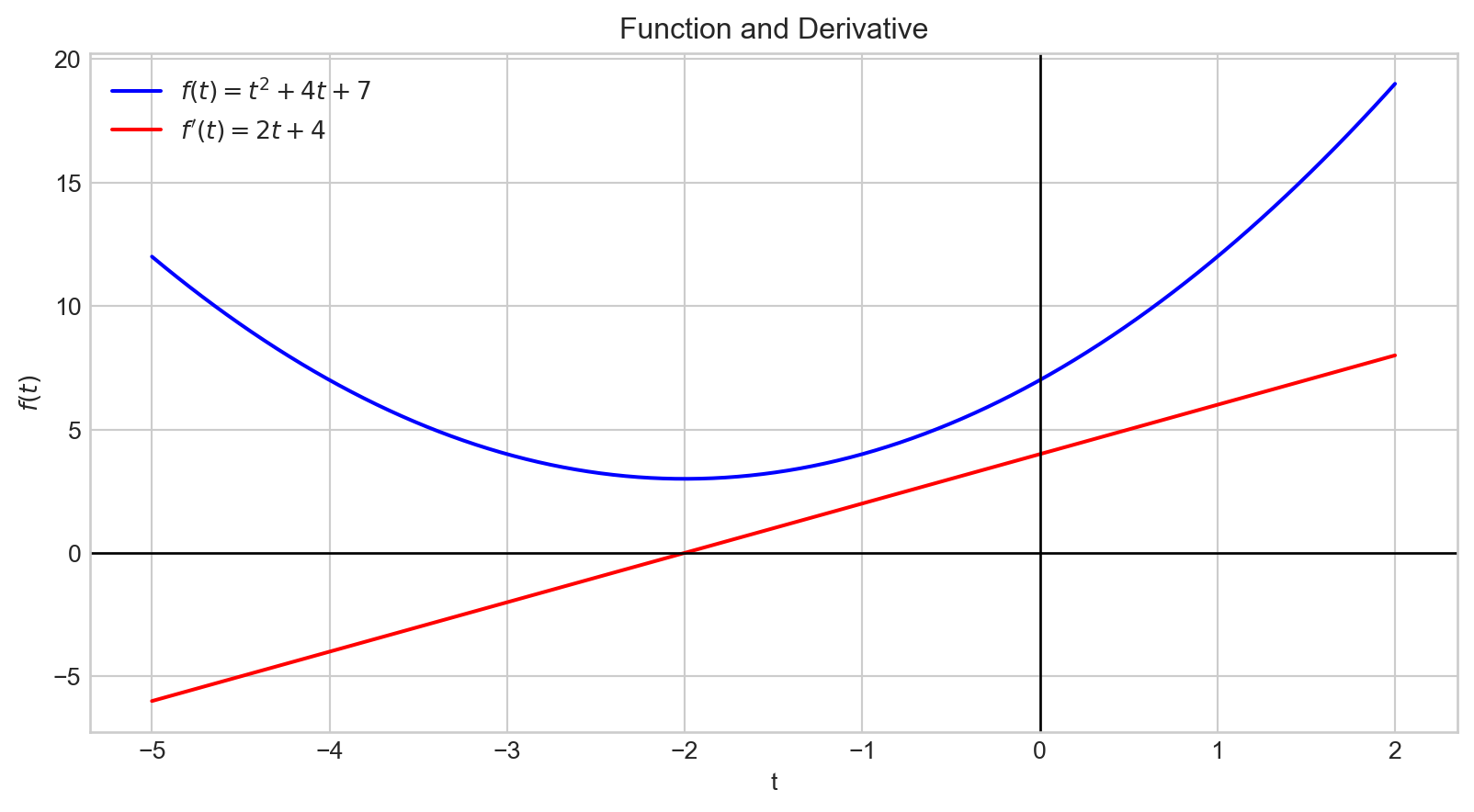
plt.show()When the value of \(\theta_j\) is in the range \([- \inf, -2)\), \(\frac {\partial}{\partial \theta_j}J(\theta)\) has a negative value.
Therefore, \(- \alpha \frac {\partial}{\partial \theta_j}J(\theta)\) is positive.
Accordingly, the value of \(\theta_j\) is increased.
Gradient Descent - Single Value
Code
import sympy as sp
import numpy as np
import matplotlib.pyplot as plt
# Define the variable and function
t = sp.symbols('t')
f = t**2 + 4*t + 7
# Compute the derivative
f_prime = sp.diff(f, t)
# Lambdify the functions for numerical plotting
f_func = sp.lambdify(t, f, "numpy")
f_prime_func = sp.lambdify(t, f_prime, "numpy")
# Generate t values for plotting
t_vals = np.linspace(-5, 2, 400)
# Get y values for the function and its derivative
f_vals = f_func(t_vals)
f_prime_vals = f_prime_func(t_vals)
# Plot the function and its derivative
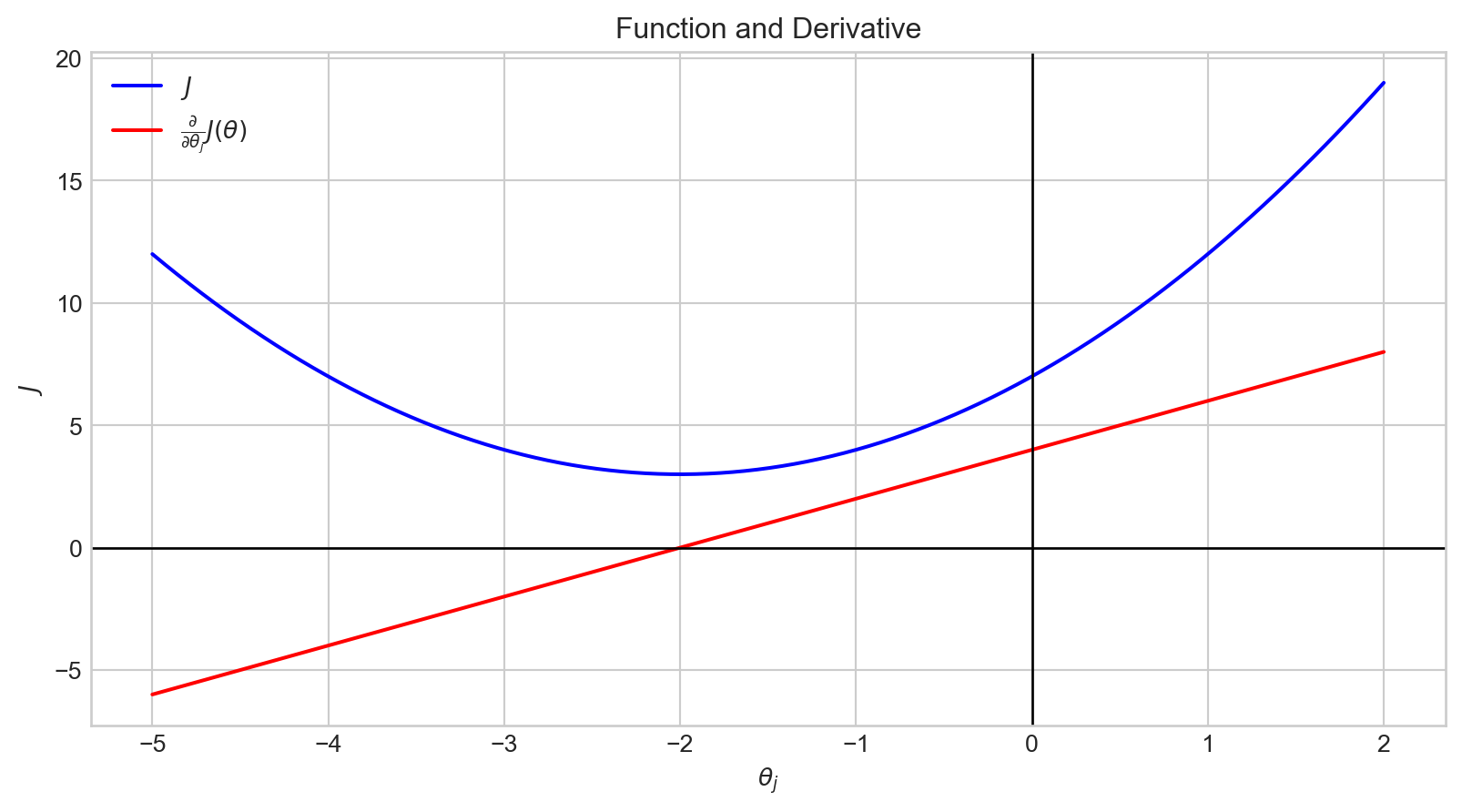
plt.plot(t_vals, f_vals, label=r'$J$', color='blue')
plt.plot(t_vals, f_prime_vals, label=r"$\frac {\partial}{\partial \theta_j}J(\theta)$", color='red')
# Add labels and legend
plt.axhline(0, color='black',linewidth=1)
plt.axvline(0, color='black',linewidth=1)
plt.title('Function and Derivative')
plt.xlabel(r'$\theta_j$')
plt.ylabel(r'$J$')
plt.legend()
# Show the plot
plt.grid(True)
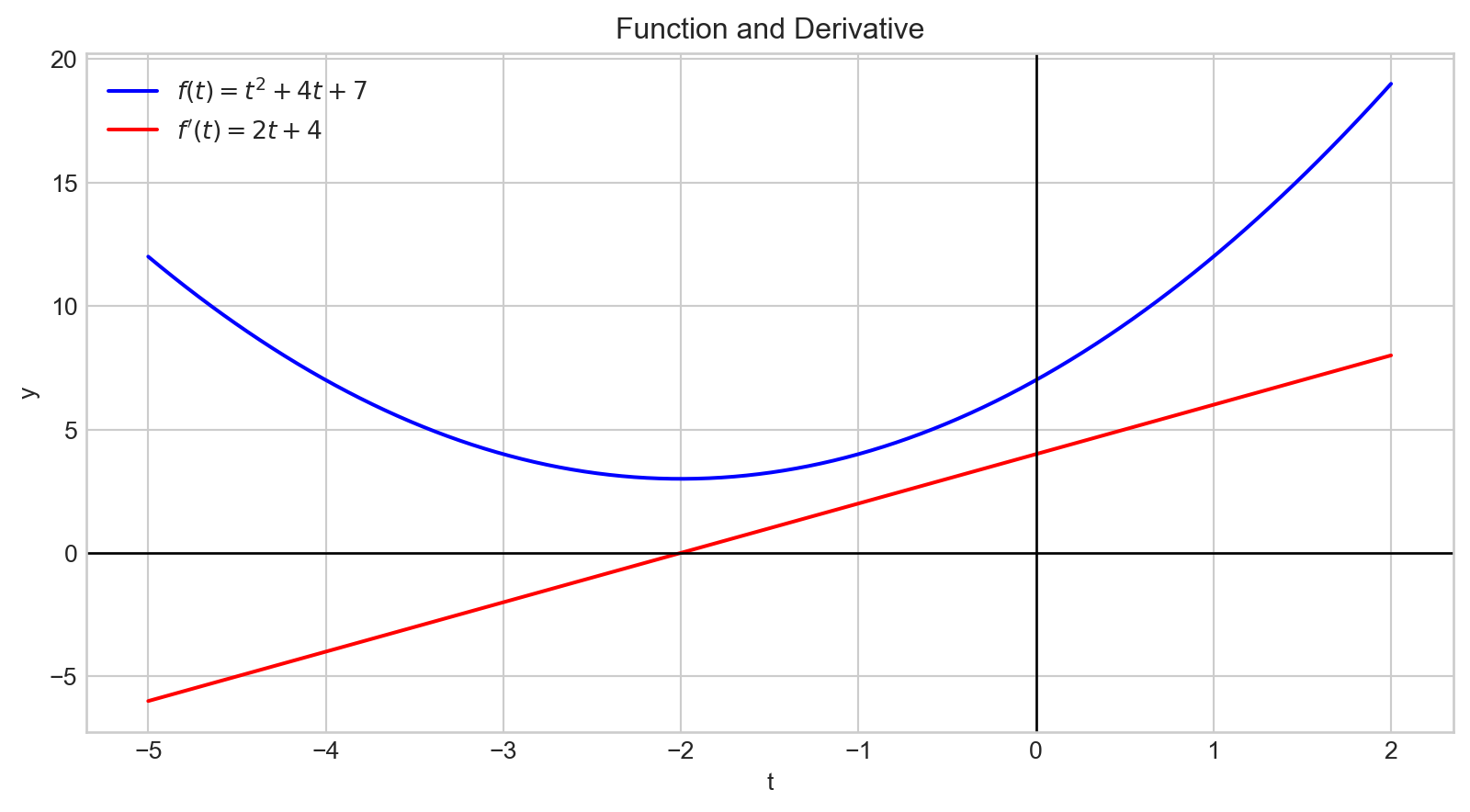
plt.show()When the value of \(\theta_j\) is in the range \((-2, \infty]\), \(\frac {\partial}{\partial \theta_j}J(\theta)\) has a positive value.
Therefore, \(- \alpha \frac {\partial}{\partial \theta_j}J(\theta)\) is negative.
Accordingly, the value of \(\theta_j\) is decreased.
Partial derivatives
Given
\[ J(\theta_0, \theta_1) = \frac{1}{N}\sum_1^N [h(x_i) - y_i]^2 = \frac{1}{N}\sum_1^N [\theta_0 + \theta_1 x_i - y_i]^2 \]
We have
\[ \frac {\partial}{\partial \theta_0}J(\theta_0, \theta_1) = \frac{2}{N} \sum\limits_{i=1}^{N} [\theta_0 - \theta_1 x_i - y_{i}] \]
and
\[ \frac {\partial}{\partial \theta_1}J(\theta_0, \theta_1) = \frac{2}{N} \sum\limits_{i=1}^{N} x_{i} [\theta_0 + \theta_1 x_i - y_{i}] \]
Partial derivate (SymPy)
Hypothesis function:\(\displaystyle h(x) = \theta_{0} + \theta_{1} x_{i}\)
Partial derivate (SymPy)
Partial derivate (SymPy)
Partial derivative with respect to theta_0:\(\displaystyle \frac{\sum_{x_{i}=1}^{N} \left(2 \theta_{0} + 2 \theta_{1} x_{i} - 2 y_{i}\right)}{N}\)
Partial derivate (SymPy)
Partial derivative with respect to theta_1:\(\displaystyle \frac{\sum_{x_{i}=1}^{N} 2 x_{i} \left(\theta_{0} + \theta_{1} x_{i} - y_{i}\right)}{N}\)
Multivariate linear regression
\[ h (x_i) = \theta_0 + \theta_1 x_i^{(1)} + \theta_2 x_i^{(2)} + \theta_3 x_i^{(3)} + \cdots + \theta_D x_i^{(D)} \]
\[ \begin{align*} x_i^{(j)} &= \text{value of the feature } j \text{ in the } i \text{th example} \\ D &= \text{the number of features} \end{align*} \]
Gradient descent - multivariate
The new loss function is
\[ J(\theta_0, \theta_1,\ldots,\theta_D) = \dfrac {1}{N} \displaystyle \sum _{i=1}^N [h(x_{i}) - y_i ]^2 \]
Its partial derivative:
\[ \frac {\partial}{\partial \theta_j}J(\theta) = \frac{2}{N} \sum\limits_{i=1}^N x_i^{(j)} [\theta x_i - y_i ] \]
where \(\theta\), \(x_i\) and \(y_i\) are vectors, and \(\theta x_i\) is a vector operation!
Gradient vector
The vector containing the partial derivative of \(J\) (with respect to \(\theta_j\), for \(j \in \{0, 1\ldots D\}\)) is called the gradient vector.
\[ \nabla_\theta J(\theta) = \begin{pmatrix} \frac {\partial}{\partial \theta_0}J(\theta) \\ \frac {\partial}{\partial \theta_1}J(\theta) \\ \vdots \\ \frac {\partial}{\partial \theta_D}J(\theta)\\ \end{pmatrix} \]
- This vector gives the direction of the steepest ascent.
- It gives its name to the gradient descent algorithm:
\[ \theta' = \theta - \alpha \nabla_\theta J(\theta) \]
Gradient descent - multivariate
The gradient descent algorithm becomes:
Repeat until convergence:
\[ \begin{aligned} \{ & \\ \theta_j := & \theta_j - \alpha \frac {\partial}{\partial \theta_j}J(\theta_0, \theta_1, \ldots, \theta_D) \\ &\text{for } j \in [0, \ldots, D] \textbf{ (update simultaneously)} \\ \} & \end{aligned} \]
Gradient descent - multivariate
Repeat until convergence:
\[ \begin{aligned} \; \{ & \\ \; & \theta_0 := \theta_0 - \alpha \frac{2}{N} \sum\limits_{i=1}^{N} x^{0}_i[h(x_i) - y_i] \\ \; & \theta_1 := \theta_1 - \alpha \frac{2}{N} \sum\limits_{i=1}^{N} x^{1}_i[h(x_i) - y_i] \\ \; & \theta_2 := \theta_2 - \alpha \frac{2}{N} \sum\limits_{i=1}^{N} x^{2}_i[h(x_i) - y_i] \\ & \cdots \\ \} & \end{aligned} \]
Assumptions
What were our assumptions?
- The (objective/loss) function is differentiable.
Local vs. global
A function is convex if for any pair of points on the graph of the function, the line connecting these two points lies above or on the graph.
- A convex function has a single minimum.
- The loss function for the linear regression (MSE) is convex.
- A convex function has a single minimum.
For functions that are not convex, the gradient descent algorithm converges to a local minimum.
The loss function generally used with linear or logistic regressions, and Support Vector Machines (SVM) are convex, but not the ones for artificial neural networks.
Local vs. global
Convergence
Code
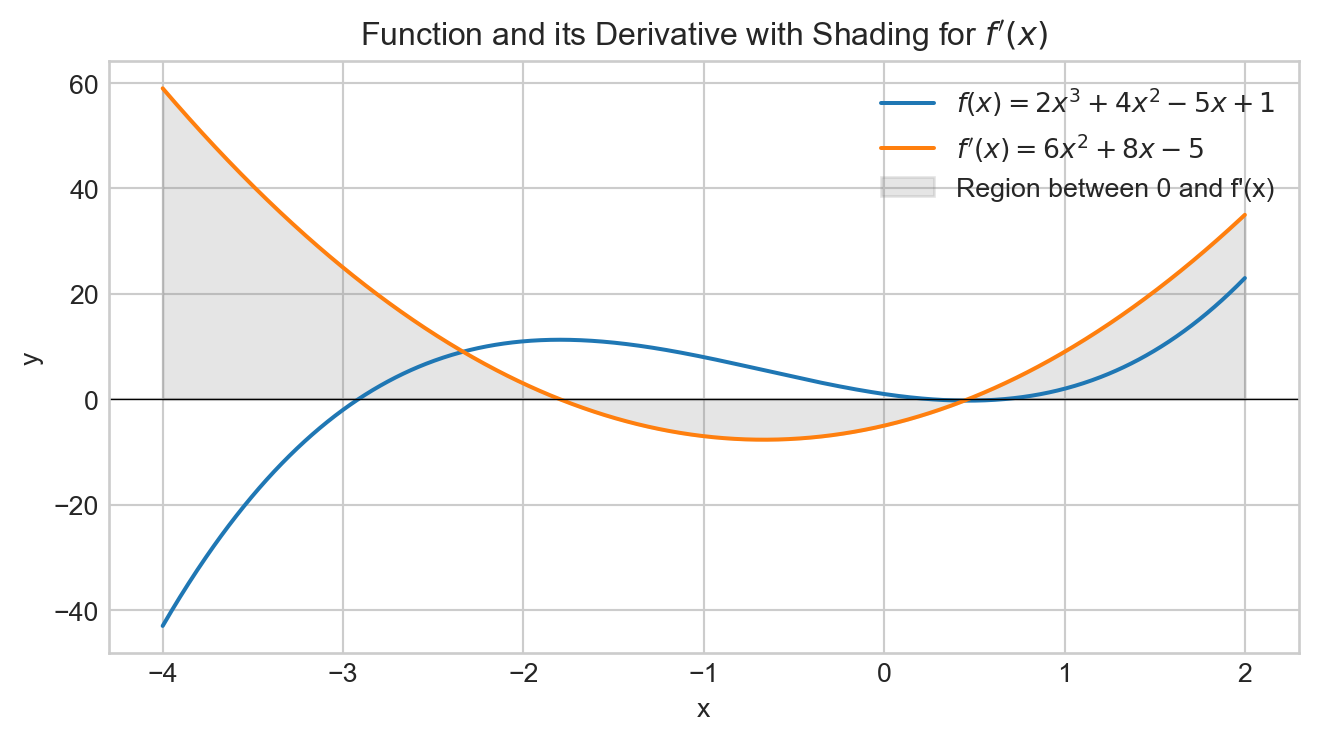
# 1. Define the symbolic variable and the function
x = sp.Symbol('x', real=True)
f_expr = 2*x**3 + 4*x**2 - 5*x + 1
# 2. Compute the derivative of f
f_prime_expr = sp.diff(f_expr, x)
# 3. Convert symbolic expressions to Python functions
f = sp.lambdify(x, f_expr, 'numpy')
f_prime = sp.lambdify(x, f_prime_expr, 'numpy')
# 4. Generate a range of x-values
x_vals = np.linspace(-4, 2, 1000)
# 5. Compute f and f' over this range
y_vals = f(x_vals)
y_prime_vals = f_prime(x_vals)
# 6. Prepare LaTeX strings for legend
f_label = rf'$f(x) = {sp.latex(f_expr)}$'
f_prime_label = rf'$f^\prime(x) = {sp.latex(f_prime_expr)}$'
# 7. Plot f and f', with equations in the legend
plt.figure(figsize=(8, 4))
plt.plot(x_vals, y_vals, label=f_label)
plt.plot(x_vals, y_prime_vals, label=f_prime_label)
# 8. Shade the region between x-axis and f'(x) for the entire domain
plt.fill_between(x_vals, y_prime_vals, 0, color='gray', alpha=0.2, interpolate=True,
label='Region between 0 and f\'(x)')
# 9. Add reference line, labels, legend, etc.
plt.axhline(0, color='black', linewidth=0.5)
plt.title(rf'Function and its Derivative with Shading for $f^\prime(x)$')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid(True)
plt.show()Learning Rate
Learning Rate
Code
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return x**2
def grad_f(x):
return 2*x
# Initial guess, learning rate, and number of gradient-descent steps
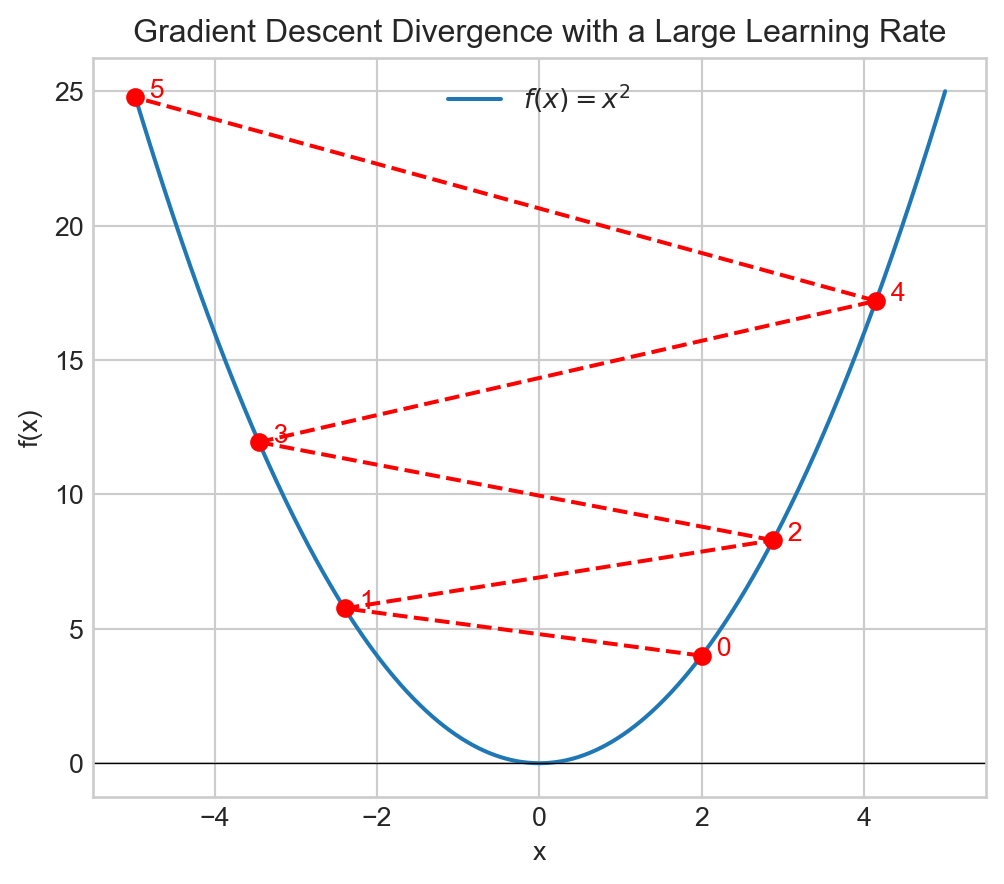
x_current = 2.0
learning_rate = 1.1 # Too large => divergence
num_iterations = 5 # We'll do five updates
# Store each x value in a list (trajectory) for plotting
trajectory = [x_current]
# Perform gradient descent
for _ in range(num_iterations):
g = grad_f(x_current)
x_current = x_current - learning_rate * g
trajectory.append(x_current)
# Prepare data for plotting
x_vals = np.linspace(-5, 5, 1000)
y_vals = f(x_vals)
# Plot the function f(x)
plt.figure(figsize=(6, 5))
plt.plot(x_vals, y_vals, label=r"$f(x) = x^2$")
plt.axhline(0, color='black', linewidth=0.5)
# Plot the trajectory, labeling each iteration
for i, x_t in enumerate(trajectory):
y_t = f(x_t)
# Plot the point
plt.plot(x_t, y_t, 'ro')
# Label the iteration number
plt.text(x_t, y_t, f" {i}", color='red')
# Connect consecutive points
if i > 0:
x_prev = trajectory[i - 1]
y_prev = f(x_prev)
plt.plot([x_prev, x_t], [y_prev, y_t], 'r--')
# Final touches
plt.title("Gradient Descent Divergence with a Large Learning Rate")
plt.xlabel("x")
plt.ylabel("f(x)")
plt.legend()
plt.grid(True)
plt.show()Batch gradient descent
- To be more precise, this algorithm is known as batch gradient descent since for each iteration, it processes the “whole batch” of training examples.
- Literature suggests that the algorithm might take more time to converge if the features are on different scales.
Batch gradient descent - drawback
- The batch gradient descent algorithm becomes very slow as the number of training examples increases.
- This is because all the training data is seen at each iteration. The algorithm is generally run for a fixed number of iterations, say 1000.
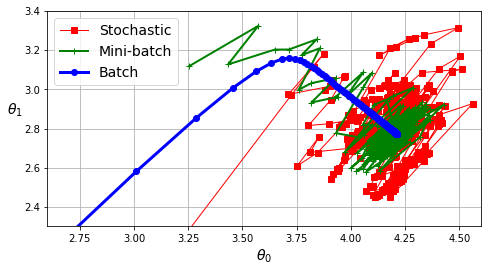
Stochastic Gradient Descent
The stochastic gradient descent algorithm randomly selects one training instance to calculate its gradient.
- This allows it to work with large training sets.
- Its trajectory is not as regular as the batch algorithm.
- Because of its bumpy trajectory, it is often better at finding the global minima, when compared to batch.
- Its bumpy trajectory makes it bounce around the local minima.
Mini-batch gradient descent
- At each step, rather than selecting one training example as SGD does, mini-batch gradient descent randomly selects a small number of training examples to compute the gradients.
- Its trajectory is more regular compared to SGD.
- As the size of the mini-batches increases, the algorithm becomes increasingly similar to batch gradient descent, which uses all the examples at each step.
- It can take advantage of the hardware acceleration of matrix operations, particularly with GPUs.
Quick Visualization
Stochastic, Mini-Batch, Batch
Summary
Batch gradient descent is inherently slow and impractical for large datasets requiring out-of-core support, though it is capable of handling a substantial number of features.
Stochastic gradient descent is fast and well-suited for processing a large volume of examples efficiently.
Mini-batch gradient descent combines the benefits of both batch and stochastic methods; it is fast, capable of managing large datasets, and leverages hardware acceleration, particularly with GPUs.
Optimization and deep nets
We will briefly revisit the subject when discussing deep artificial neural networks, for which specialized optimization algorithms exist.
- Momentum Optimization
- Nesterov Accelerated Gradient
- AdaGrad
- RMSProp
- Adam and Nadam
Final word
- Optimization is a vast subject. Other algorithms exist and are used in other contexts.
- Including:
- Particle swarm optimization (PSO), genetic algorithms (GAs), and artificial bee colony (ABC) algorithms.
- Including:
Prologue
Linear regression - summary
- A linear model assumes that the value of the label, \(\hat{y_i}\), can be expressed as a linear combination of the feature values, \(x_i^{(j)}\): \(\hat{y_i} = h(x_i) = \theta_0 + \theta_1 x_i^{(1)} + \theta_2 x_i^{(2)} + \ldots + \theta_D x_i^{(D)}\)
- The Mean Squared Error (MSE) is: \(\frac{1}{N}\sum_1^N [h(x_i) - y_i]^2\)
- Batch, stochastic, or mini-batch gradient descent can be used to find “optimal” values for the parameters, \(\theta_j\) for \(j \in 0, 1, \ldots, D\).
- The result is a regressor, a function that can be used to predict the \(y\) value (the label) for some unseen example \(x\).
Andrew Ng
- Gradient Descent (Math)
(11:30 m) - Intuition
(11:51 m) - Linear Regression
(10:20 m) - ML-005 | Stanford | Andrew Ng
(19 videos)
Fundamentals by Herman Kamper
Mathematics
3Blue1Brown
- Essence of linear algebra
- A series of 16 videos (10 to 15 minutes per video) providing “a geometric understanding of matrices, determinants, eigen-stuffs and more.”
- 6,662,732 views as of September 30, 2019.
- A series of 16 videos (10 to 15 minutes per video) providing “a geometric understanding of matrices, determinants, eigen-stuffs and more.”
- Essence of calculus
- A series of 12 videos (15 to 20 minutes per video): “The goal here is to make calculus feel like something that you yourself could have discovered.”
- 2,309,726 views as of September 30, 2019.
- A series of 12 videos (15 to 20 minutes per video): “The goal here is to make calculus feel like something that you yourself could have discovered.”
Next lecture
- Logistic regression
Appendix
LinearRegression
Source code
GPT 4o interactions (2024-09-14)
User: Explain the code on the previous slide line by line.
AI: Certainly! Here is a line-by-line explanation of the provided code:
- Explanation: This line imports the NumPy library, which is a fundamental package for numerical computations in Python. It is commonly used for working with arrays and matrices, as well as for performing a variety of mathematical operations.
- Explanation: This line generates a NumPy array
Xcontaining 100 rows and 1 column of random numbers. Thenp.random.rand(100, 1)function generates uniformly distributed random numbers between 0 and 1. Multiplying by 6 scales these numbers to the range [0, 6), and subtracting 4 shifts the range to [-4, 2).
- Explanation: This line generates the target variable
ybased on a quadratic equation with some added noise. Specifically:X ** 2computes the square of each element inX.- 4 * Xsubtracts four times each element inX.+ 5adds a constant term of 5.+ np.random.randn(100, 1)adds Gaussian noise with a mean of 0 and standard deviation of 1 to each element, making the data more realistic by introducing some randomness.
- Explanation: This line imports the
LinearRegressionclass from thesklearn.linear_modelmodule, which is part of the Scikit-Learn library. Scikit-Learn is widely used for machine learning in Python.
- Explanation: This line creates an instance of the
LinearRegressionclass and assigns it to the variablelin_reg. This object will be used to fit the linear regression model to the data.
- Explanation: This line fits the linear regression model to the data by finding the best-fitting line through the points
(X, y). Thefitmethod trains the model using the provided featuresXand target variabley.
- Explanation: This line creates a new NumPy array
X_newwith two values: -4 and 2. These values represent new data points for which we want to predict the target variable using the trained model.
- Explanation: This line uses the trained linear regression model to predict the target variable
y_predfor the new data points inX_new. Thepredictmethod returns the predicted values based on the fitted model.
In summary, this script generates synthetic data, fits a linear regression model to it, and then uses the model to make predictions on new data points.
Source code (continued)
import os
import matplotlib as mpl
import matplotlib.pyplot as plt
def save_fig(fig_id, tight_layout=True, fig_extension="pdf", resolution=300):
path = os.path.join(fig_id + "." + fig_extension)
print("Saving figure", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format=fig_extension, dpi=resolution)Source code (continued)
References
Marcel Turcotte
School of Electrical Engineering and Computer Science (EECS)
University of Ottawa