Machine Learning Engineering
CSI 4106 - Fall 2025
Version: Oct 5, 2025 12:29
Preamble
Message of the Day
Learning Objectives
- Explain feature extraction, compare encoding methods, and justify choices based on data nature.
- Apply normalization/standardization for feature scaling and handle missing values using imputation.
- Define class imbalance, explore solutions like resampling and SMOTE, and ensure proper application.
- Apply concepts to real-world datasets, analyze results, and understand the machine learning pipeline.
- Recognize dataset size impact, discuss data augmentation, and explore data effectiveness in ML.
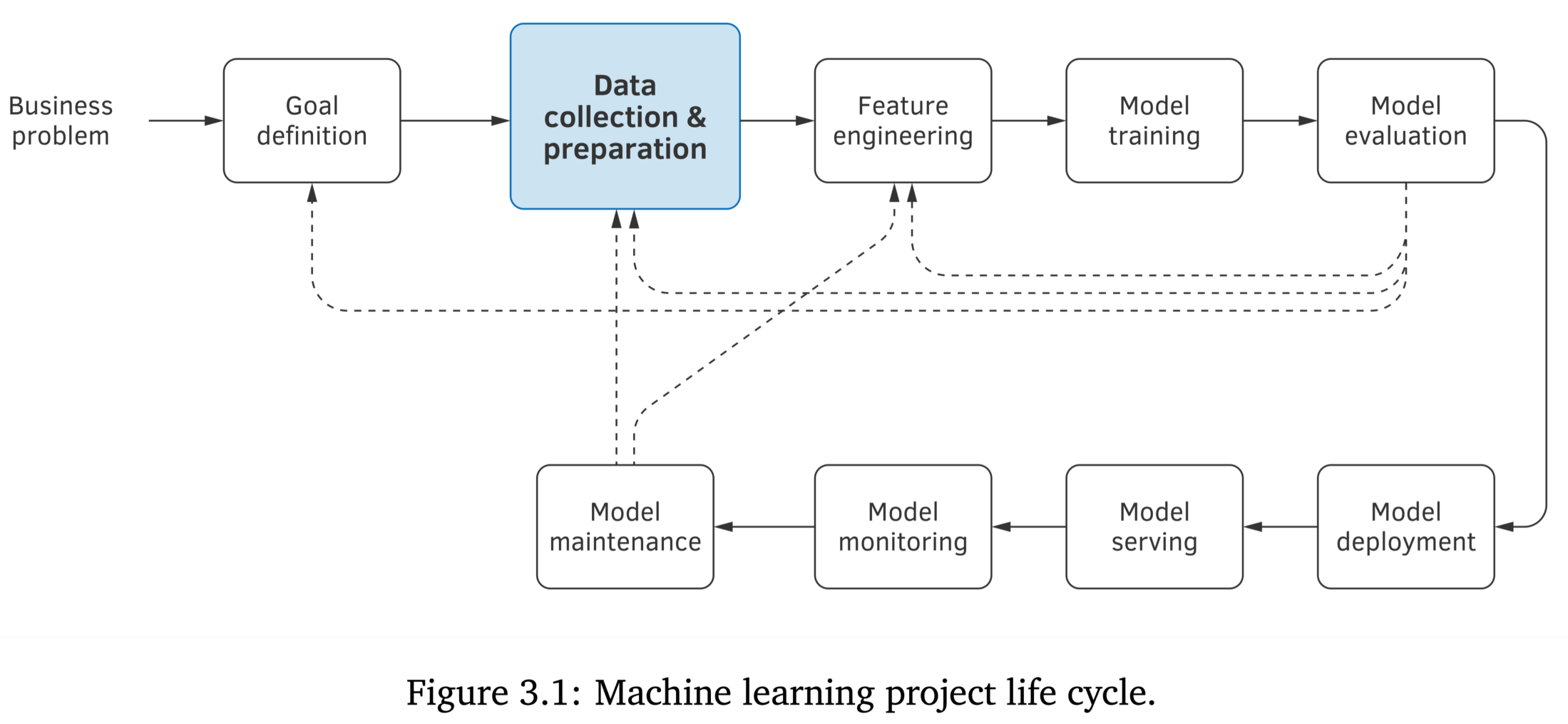
Machine Learning Engineering
Machine Learning Engineering
Encoding
Why?
After completing Assignment 1, you generated a .csv file containing cleaned data.
Why would additional steps be necessary?
Dataset - Adult
Dataset - Adult
Author: Ronny Kohavi and Barry Becker
Source: UCI - 1996
Please cite: Ron Kohavi, “Scaling Up the Accuracy of Naive-Bayes Classifiers: a Decision-Tree Hybrid”, Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, 1996
Prediction task is to determine whether a person makes over 50K a year. Extraction was done by Barry Becker from the 1994 Census database. A set of reasonably clean records was extracted using the following conditions: ((AAGE>16) && (AGI>100) && (AFNLWGT>1)&& (HRSWK>0))
This is the original version from the UCI repository, with training and test sets merged.
Variable description
Variables are all self-explanatory except fnlwgt. This is a proxy for the demographic background of the people: “People with similar demographic characteristics should have similar weights”. This similarity-statement is not transferable across the 51 different states.
Description from the donor of the database:
The weights on the CPS files are controlled to independent estimates of the civilian noninstitutional population of the US. These are prepared monthly for us by Population Division here at the Census Bureau. We use 3 sets of controls. These are: 1. A single cell estimate of the population 16+ for each state. 2. Controls for Hispanic Origin by age and sex. 3. Controls by Race, age and sex.
We use all three sets of controls in our weighting program and “rake” through them 6 times so that by the end we come back to all the controls we used. The term estimate refers to population totals derived from CPS by creating “weighted tallies” of any specified socio-economic characteristics of the population. People with similar demographic characteristics should have similar weights. There is one important caveat to remember about this statement. That is that since the CPS sample is actually a collection of 51 state samples, each with its own probability of selection, the statement only applies within state.
Relevant papers
Ronny Kohavi and Barry Becker. Data Mining and Visualization, Silicon Graphics.
e-mail: ronnyk ‘@’ live.com for questions.
Downloaded from openml.org.
Adult - Workclass
['Private', 'Local-gov', NaN, 'Self-emp-not-inc', 'Federal-gov', 'State-gov', 'Self-emp-inc', 'Without-pay', 'Never-worked']
Categories (8, object): ['Federal-gov', 'Local-gov', 'Never-worked', 'Private', 'Self-emp-inc', 'Self-emp-not-inc', 'State-gov', 'Without-pay']Adult - Education
Adult - Marital Status
['Never-married', 'Married-civ-spouse', 'Widowed', 'Divorced', 'Separated', 'Married-spouse-absent', 'Married-AF-spouse']
Categories (7, object): ['Divorced', 'Married-AF-spouse', 'Married-civ-spouse', 'Married-spouse-absent', 'Never-married', 'Separated', 'Widowed']Categorical Data
Key Points on Data Representation
- Numerical Representation: Some learning algorithms require data to be in numerical form.
Encoding Methods
Consider the workclass attribute, which has 8 distinct values like ‘Federal-gov’, ‘Local-gov’, and so on.
- Which encoding method is preferable and why?
w= 1, 2, 3, 4, 5, 6, 7, or 8w= [0,0,0], [0,0,1], [0,1,0], \(\ldots\), or [1,1,1]w= [1,0,0,0,0,0,0,0], [0,1,0,0,0,0,0,0], \(\ldots\), or [0,0,0,0,0,0,0,1]
Encoding for Categorical Data
One-Hot Encoding: This method should be preferred for categorical data.
- Increases Dimensionality: One-hot encoding increases the dimensionality of feature vectors.
- Avoids Bias: Other encoding methods can introduce biases.
- Example of Bias: Using the first method,
w= 1, 2, 3, etc., implies that ‘Federal-gov’ and ‘Local-gov’ are similar, while ‘Federal-gov’ and ‘Without-pay’ are not. - Misleading Similarity: The second method,
w= [0,0,0], [0,0,1], etc., might mislead the algorithm by suggesting similarity based on numeric patterns.
Definition
One-Hot Encoding: A technique that converts categorical variables into a binary vector representation, where each category is represented by a vector with a single ‘1’ and all other elements as ‘0’.
OneHotEncoder
[0. 0. 0. 1. 0. 0. 0. 0. 0.]
[0. 0. 0. 1. 0. 0. 0. 0. 0.]
[0. 1. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 1. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 1.]Case Study
- Dataset: Heart Disease
- Examples: 303, features: 13, target: Presence/absence of disease
- Categorical Data:
- sex: 1 = male, 0 = female
- cp (chest pain type):
- 1: Typical angina
- 2: Atypical angina
- 3: Non-anginal pain
- 4: Asymptomatic
- Other: ‘fbs’, ‘restecg’, ‘exang’, ‘slope’, ‘thal’
Case Study
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_openml
from sklearn.preprocessing import OneHotEncoder, StandardScaler
from sklearn.compose import ColumnTransformer
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
# Load the 'Heart-Disease' dataset from OpenML
data = fetch_openml(name='Heart-Disease', version=1, as_frame=True)
df = data.frame
# Replace '?' with NaN and convert columns to numeric
for col in df.columns:
df[col] = pd.to_numeric(df[col], errors='coerce')
# Drop rows with missing values
df.dropna(inplace=True)
# Define features and target
X = df.drop(columns=['target'])
y = df['target']
# Columns to encode with OneHotEncoder
columns_to_encode = ['sex', 'cp', 'fbs', 'restecg', 'exang', 'slope', 'thal']
# Identify numerical columns
numerical_columns = X.columns.difference(columns_to_encode)
# Split the dataset into training and testing sets before transformations
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=42
)
# Apply OneHotEncoder and StandardScaler using ColumnTransformer
column_transformer = ColumnTransformer(
transformers=[
('onehot', OneHotEncoder(), columns_to_encode),
('scaler', StandardScaler(), numerical_columns)
]
)
# Fit the transformer on the training data and transform both training and test data
X_train_processed = column_transformer.fit_transform(X_train)
X_test_processed = column_transformer.transform(X_test)
# Initialize and train logistic regression model
model = LogisticRegression(max_iter=1000)
model = model.fit(X_train_processed, y_train)Case study - results
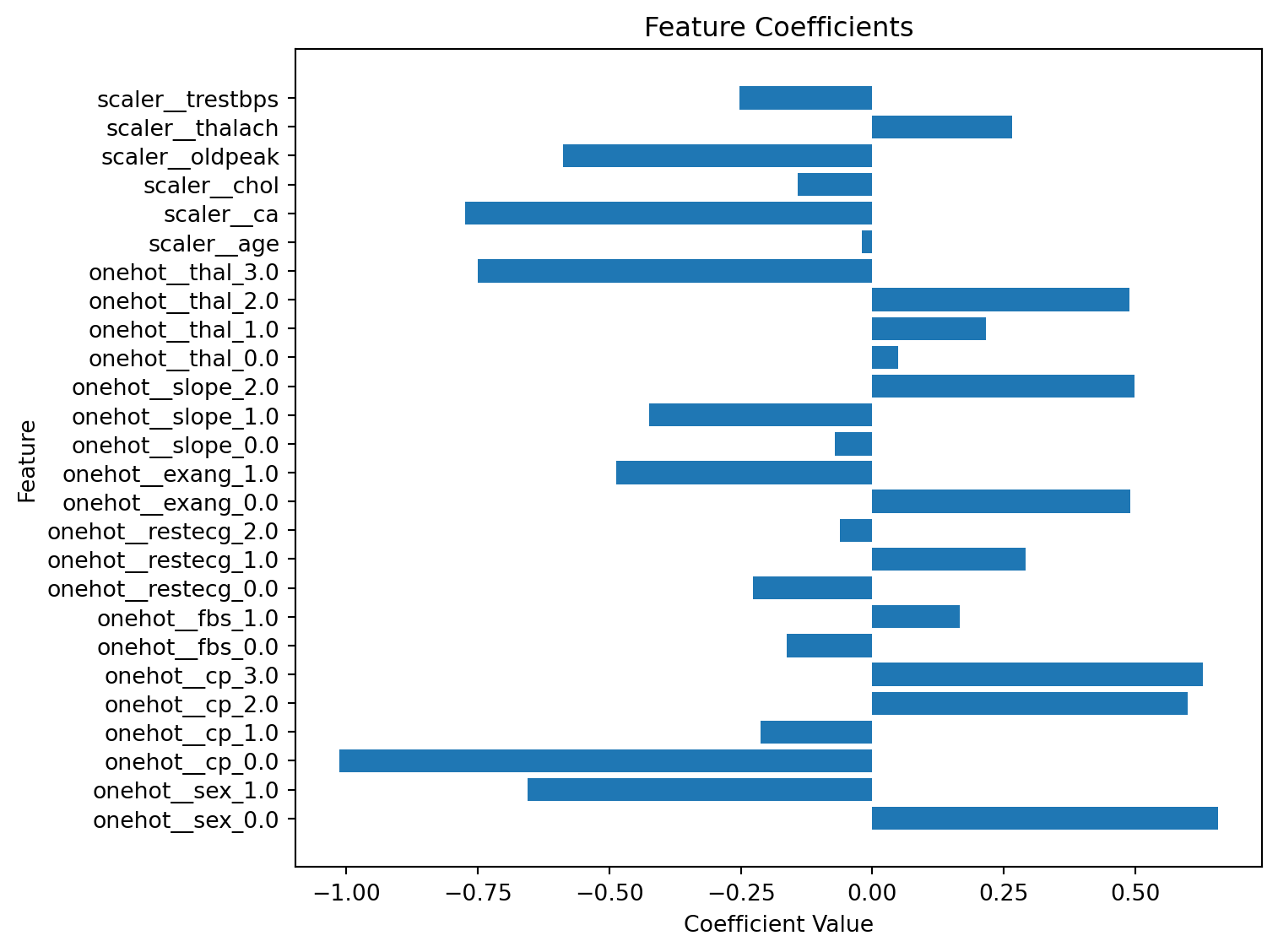
Case study - chest pain (cp)
# Retrieve feature names after transformation using get_feature_names_out()
feature_names = column_transformer.get_feature_names_out()
# Get coefficients and map them to feature names
coefficients = model.coef_[0]
# Create a DataFrame with feature names and coefficients
coef_df = pd.DataFrame({
'Feature': feature_names,
'Coefficient': coefficients
})
# Display coefficients associated with 'cp'
cp_features = coef_df[coef_df['Feature'].str.contains('_cp')]
print("\nCoefficients associated with 'cp':")
print(cp_features)
Coefficients associated with 'cp':
Feature Coefficient
2 onehot__cp_0.0 -1.013382
3 onehot__cp_1.0 -0.212284
4 onehot__cp_2.0 0.599934
5 onehot__cp_3.0 0.628824Case study - coefficients
Case study - coefficients
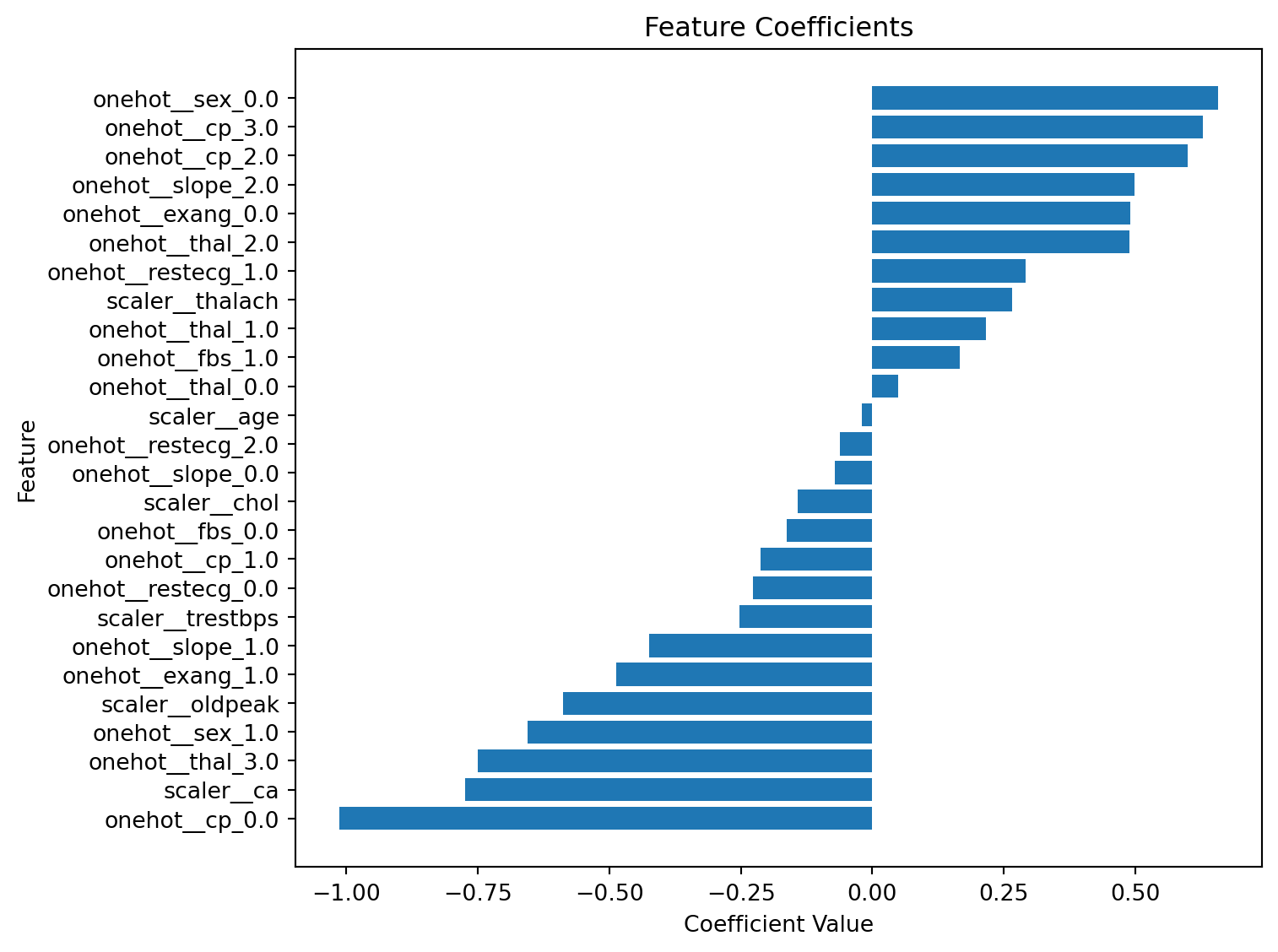
Case study - coefficients (sorted)
Case study - coefficients (sorted)
Definition
Ordinal encoding is a technique that assigns numerical values to categorical attributes based on their inherent order or rank.
Feature Engineering - Ordinal
For attributs with values such as ‘Poor’, ‘Average’, and ‘Good’, an ordinal encoding would make sense.
OrdinalEncoder (revised)
Definition
Discretization involves grouping ordinal values into discrete categories.
Feature Engineering: Binning
Example: Categorizing ages into bins such as ‘infant’, ‘child’, ‘teen’, ‘adult’, and ‘senior citizen’.
Advantages:
- Enables the algorithm to learn effectively with fewer training examples.
Disadvantages:
- Requires domain expertise to define meaningful categories.
- May lack generalizability; for example, the starting age for ‘senior citizen’ could be 60, 65, or 701.
FunctionTransformer
import pandas as pd
import numpy as np
from sklearn.preprocessing import FunctionTransformer
bins = [0, 1, 13, 20, 60, np.inf]
labels = ['infant', 'kid', 'teen', 'adult', 'senior citizen']
transformer = FunctionTransformer(
pd.cut, kw_args={'bins': bins, 'labels': labels, 'retbins': False}
)
X = np.array([0.5, 2, 15, 25, 97])
transformer.fit_transform(X)['infant', 'kid', 'teen', 'adult', 'senior citizen']
Categories (5, object): ['infant' < 'kid' < 'teen' < 'adult' < 'senior citizen']Scaling
What is it?
Scaling attributes ensures that their values fall within comparable ranges.
Why?
Why is scaling data a best practice?
Scenario
We pretend to predict a house price using k-Nearest Neighbors (KNN) regression with two features:
- \(x_1\): number of rooms (small scale)
- \(x_2\): square footage (large scale)
Data (three houses)
import numpy as np
import pandas as pd
# Three examples (rooms, sqft); prices only for b and c (training)
point_names = ["a", "b", "c"]
X = np.array([
[4, 1500.0], # a (query)
[8, 1520.0], # b (train)
[4, 1300.0], # c (train)
], dtype=float)
prices = pd.Series([np.nan, 520_000, 390_000], index=point_names, name="price")
df = pd.DataFrame(X, columns=["rooms", "sqft"], index=point_names)
display(df)
display(prices.to_frame())Note. We’ll treat b and c as the training set, and a as the query whose price we want to predict.
Data (three houses)
| rooms | sqft | |
|---|---|---|
| a | 4.0 | 1500.0 |
| b | 8.0 | 1520.0 |
| c | 4.0 | 1300.0 |
| price | |
|---|---|
| a | NaN |
| b | 520000.0 |
| c | 390000.0 |
Euclidean distances (unscaled)
When one feature has a much larger scale (e.g., square footage), it can dominate the sum.
Euclidean distances (unscaled)
| a | b | c | |
|---|---|---|---|
| a | 0.000000 | 20.396078 | 200.000000 |
| b | 20.396078 | 0.000000 | 220.036361 |
| c | 200.000000 | 220.036361 | 0.000000 |
Proper scaling for modeling
For a fair ML workflow, compute scaling parameters on the training data (b, c) only, then transform both train and query:
Proper scaling for modeling
| rooms | sqft | |
|---|---|---|
| a | -1.0 | 0.818182 |
| b | 1.0 | 1.000000 |
| c | -1.0 | -1.000000 |
Euclidean distances (after scaling)
| a | b | c | |
|---|---|---|---|
| a | 0.000000 | 2.008247 | 1.818182 |
| b | 2.008247 | 0.000000 | 2.828427 |
| c | 1.818182 | 2.828427 | 0.000000 |
KNN regressor
We’ll run a 1-NN regressor (so the prediction is exactly the nearest neighbor’s price) with and without scaling.
KNN regressor (no scaling)
KNN regressor (with scaling)
KNN regressor (results)
pd.DataFrame(
{
"prediction (no scaling)": [pred_plain],
"prediction (with scaling)": [pred_scaled],
"nearest neighbor (no scaling)": [point_names[1] if pred_plain==prices['b'] else point_names[2]],
"nearest neighbor (with scaling)": [point_names[1] if pred_scaled==prices['b'] else point_names[2]],
},
index=["a"]
)| prediction (no scaling) | prediction (with scaling) | nearest neighbor (no scaling) | nearest neighbor (with scaling) | |
|---|---|---|---|---|
| a | 520000.0 | 390000.0 | b | c |
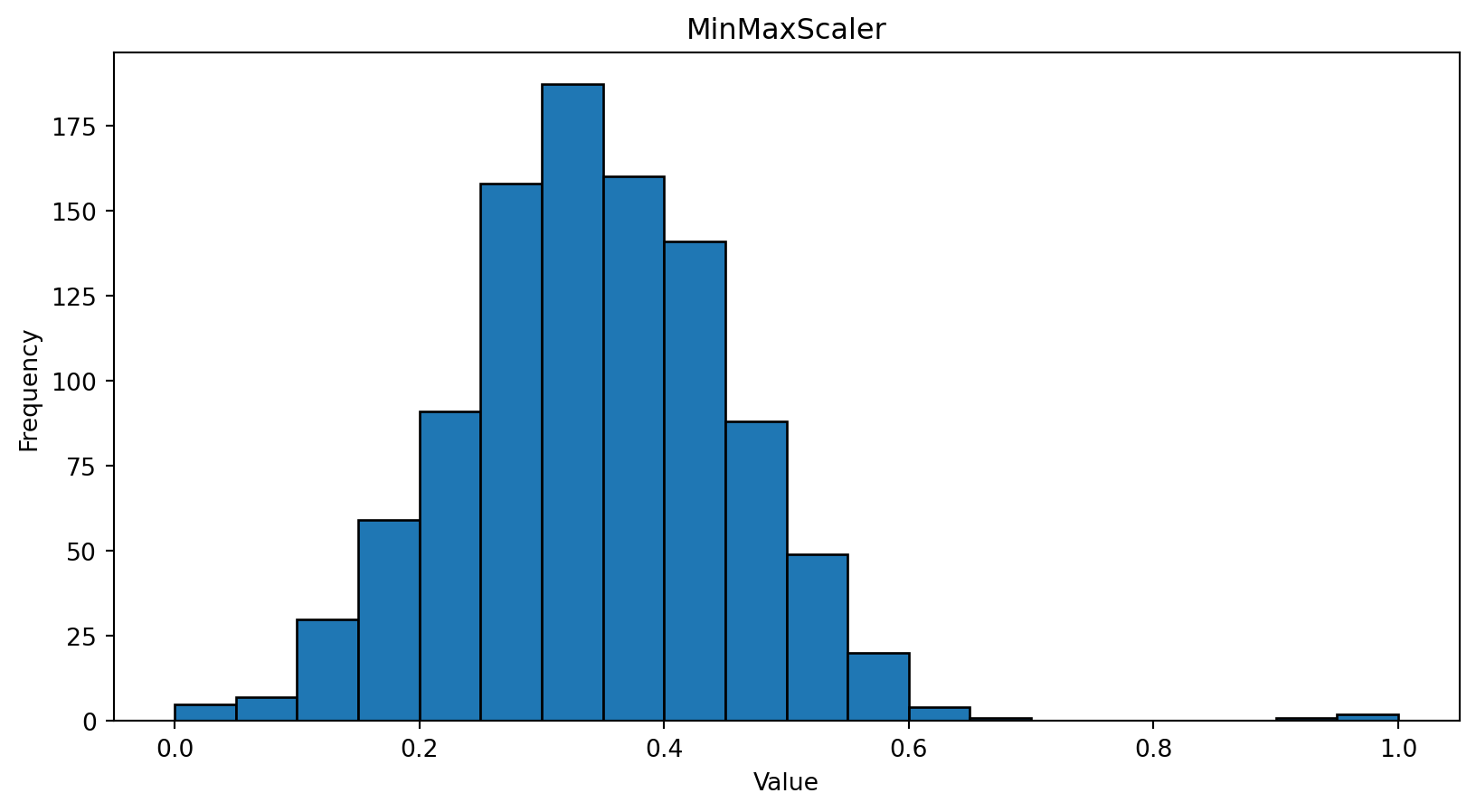
Normalization
Learning algorithms perform optimally when feature values have similar ranges, such as [-1,1] or [0,1].
- This accelerates optimization (e.g., gradient descent).
Normalization: \[ \frac{x_i^{(j)} - \min^{(j)}}{\max^{(j)} - \min^{(j)}} \]
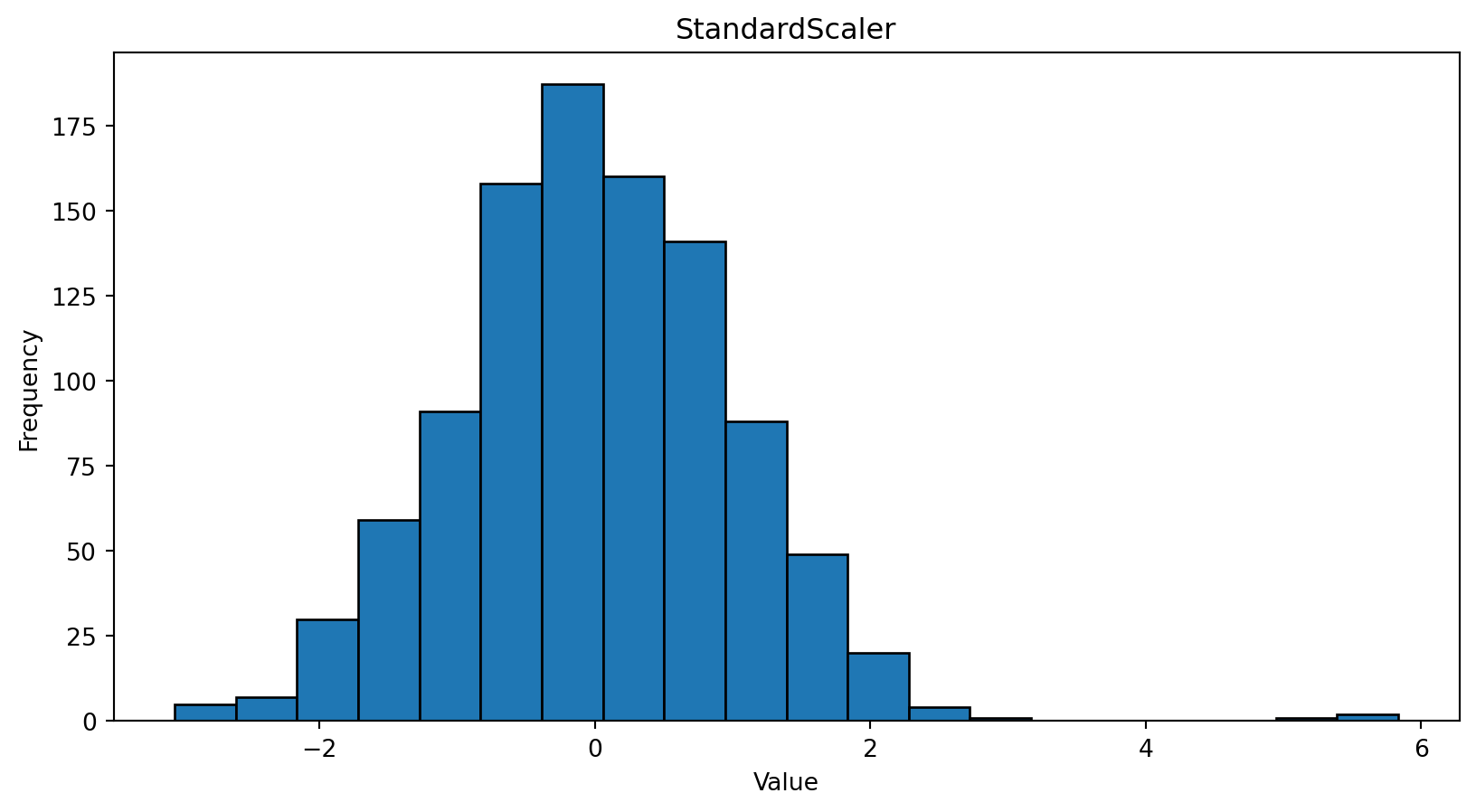
Standardization
Standardization (AKA z-score normalization) transforms each feature to have a normal distribution with a mean (\(\mu\)) of 0 and a standard deviation (\(\sigma\)) of 1.
\[ \frac{x_i^{(j)} - \mu^{(j)}}{\sigma^{(j)}} \]
Note: The range of values is not bounded!
Standardization or Normalization?
- Treat scaling as a hyperparameter and evaluate both normalization and standardization.
- Standardization is generally more robust to outliers than normalization.
- Guidelines from Andriy Burkov (2019), § 5:
- Use standardization if features are approximately normally distributed.
- Prefer standardization in the presence of outliers.
- Otherwise, use normalization.
| Feature | Standardization | Normalization |
|---|---|---|
| Output Range | Not bounded | Typically [0, 1] |
| Center | Mean at 0 | Not centered |
| Sensitivity to Outliers | Low | High |
| Primary Use Case | Default choice; for models assuming zero-centered data | When bounded input is required (e.g., image processing, some neural networks) |
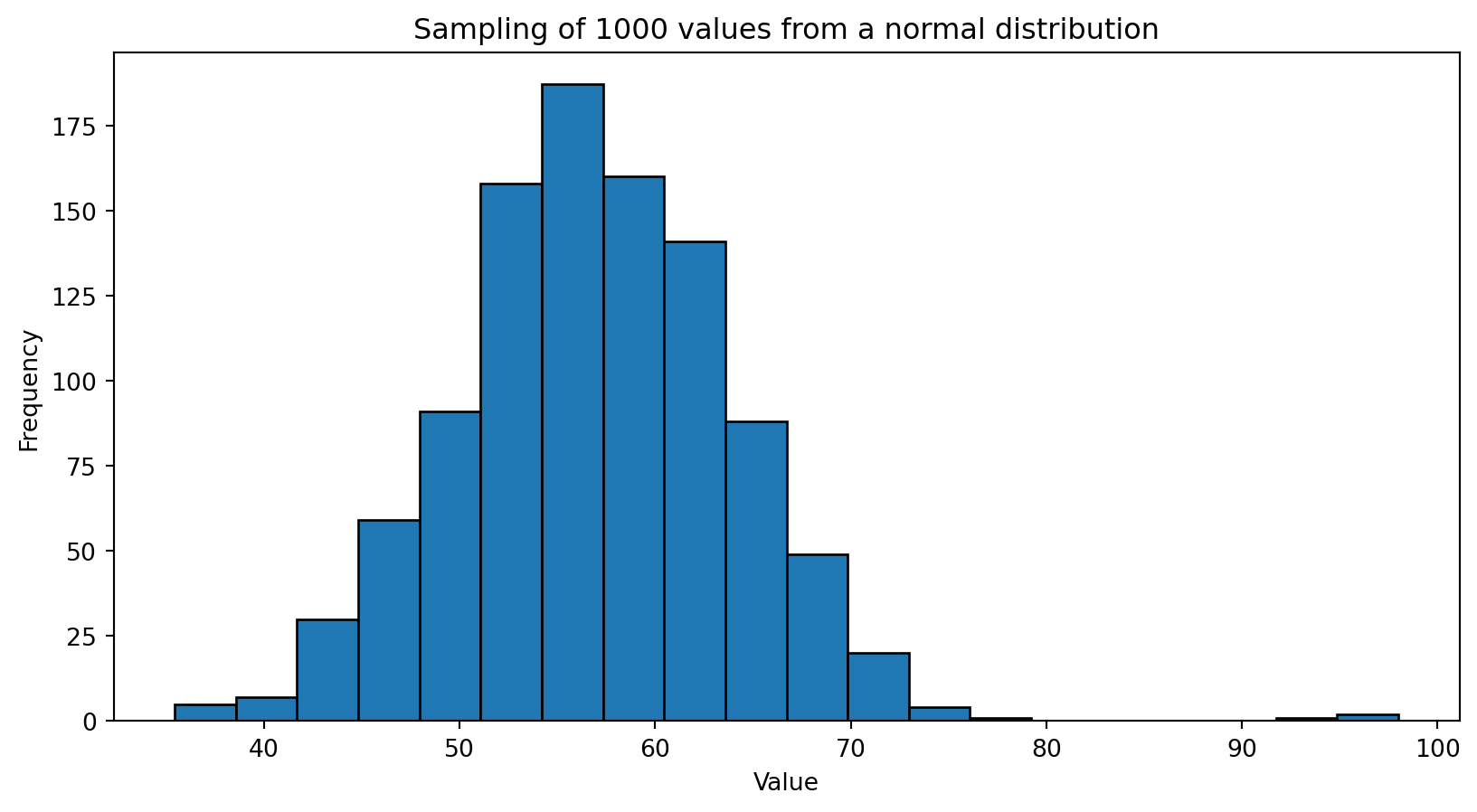
Case Study - Normal Distribution
Case Study - Normal Distribution
Normalization
Standardization
Avoid Data Leakage!
The correct workflow:
- Split your data into a training set and a testing set.
- Fit your scaler (e.g.,
StandardScaler) on the training data (scaler.fit(X_train)).- This step learns the mean and standard deviation of the training data.
- Transform both the training data (
scaler.transform(X_train)) and the testing data (scaler.transform(X_test)) using the scaler that was fitted on the training data.
Missing Values
Definition
Missing values refer to the absence of data points or entries in a dataset where a value is expected.
Handling Missing Values
- Drop Examples
- Feasible if the dataset is large and outcome is unaffected.
- Drop Features
- Suitable if it does not impact the project’s outcome.
- Use Algorithms Handling Missing Data
- Example:
XGBoost - Note: Some algorithms like
sklearn.linear_model.LinearRegressioncannot handle missing values.
- Example:
- Data Imputation
- Replace missing values with computed values.
Definition
Data imputation is the process of replacing missing values in a dataset with substituted values, typically using statistical or machine learning methods.
Data Imputation Strategy
Replace missing values with mean or median of the attribute.
Cons: Ignores feature correlations and complex relationships.
Mode Imputation: Replace missing values with the most frequent value; also ignores feature correlations.
Data Imputation Strategy
Special Value Method: Replace missing values with a value outside the normal range (e.g., use -1 or 2 for data normalized between [0,1]).
- Objective: Enable the learning algorithm to recognize and appropriately handle missing values.
Alternative Approach
- Problem Definition: Predict unknown (missing) labels for given examples.
- Have you encountered this kind of problem before?
- Relevance: This can be framed as a supervised learning problem.
- Let \(\hat{x_i}\) be a new example: \([x_i^{(1)}, x_i^{(2)}, \ldots, x_i^{(j-1)}, x_i^{(j+1)}, \ldots, x_i^{(D)}]\).
- Let \(\hat{y}_i = x_i^{j}\).
- Training Set: Use examples where \(x_i^{j}\) is not missing.
- Method: Train a classifier on this set to predict (impute) the missing values.
Using ML for Imputation
Instance-Based Method:
- Use \(k\) nearest neighbors (k-NN) to find the \(k\) closest examples and impute using the non-missing values from the neighborhood.
Model-Based Methods:
- Employ advanced techniques such as random forests, tensor decomposition, or deep neural networks.
Why Use these Methods?
- Advantages:
- Effectively handle complex relationships and correlations between features.
- Disadvantages:
- Cost-intensive in terms of labor, CPU time, and memory resources.
Class Imbalance
Definition
The class imbablance problem is a scenario where the number of instances in one class significantly outnumbers the instances in other classes.
Models tend to be biased towards the majority class, leading to poor performance on the minority class.
Solutions
Resampling: Techniques such as oversampling the minority class or undersampling the majority class.
Algorithmic Adjustments: Using cost-sensitive learning or modifying decision thresholds.
- See
class_weightfor SGDClassifier.
- See
Synthetic Data: Generating synthetic samples for the minority class using methods like SMOTE (Synthetic Minority Over-sampling Technique).
Apply solutions only to the training set to prevents data leakage!
New Features
Definition
Feature engineering is the process of creating, transforming, and selecting variables (attributes) from raw data to improve the performance of machine learning models.
Exploration
Code
import numpy as np
np.random.seed(42)
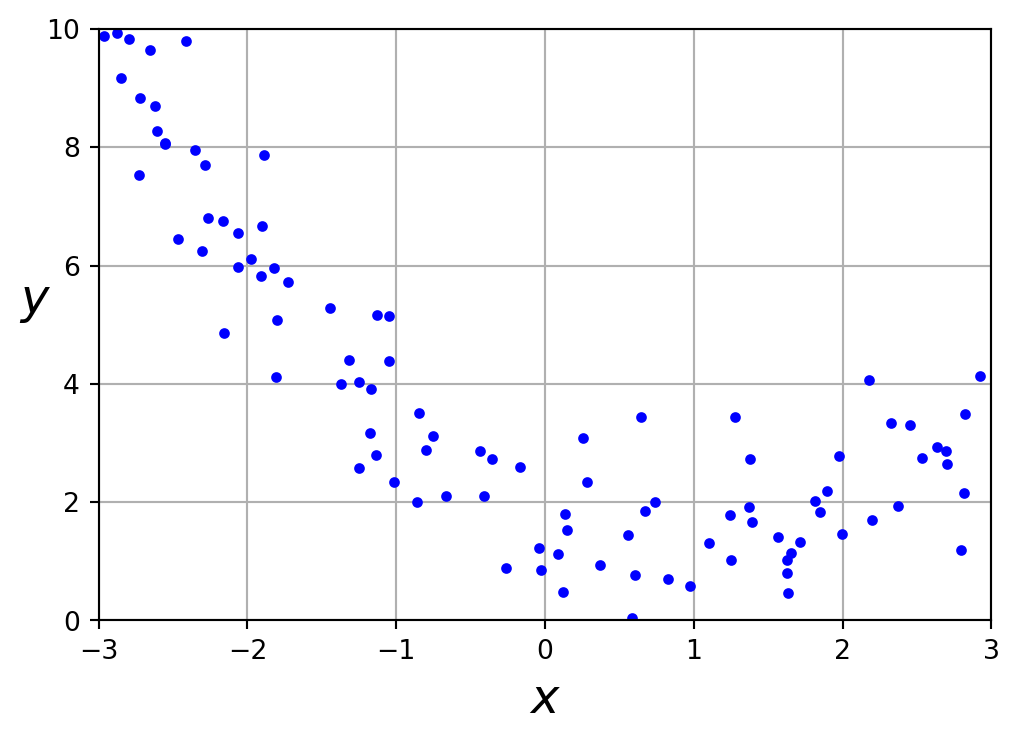
X = 6 * np.random.rand(100, 1) - 3
y = 0.5 * X ** 2 - X + 2 + np.random.randn(100, 1)
import matplotlib as mpl
import matplotlib.pyplot as plt
plt.figure(figsize=(6,4))
plt.plot(X, y, "b.")
plt.xlabel("$x$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([-3, 3, 0, 10])
plt.grid(True)
plt.show()Linear Regression
Code
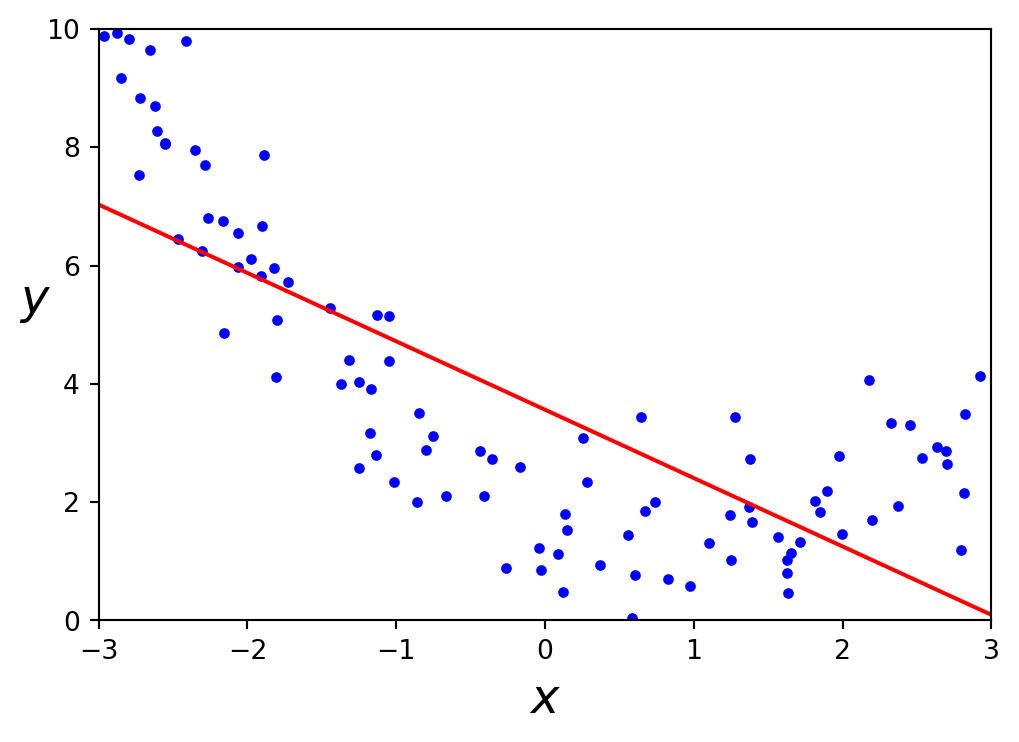
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X, y)
X_new = np.array([[-3], [3]])
y_pred = lin_reg.predict(X_new)
plt.figure(figsize=(6,4))
plt.plot(X, y, "b.")
plt.plot(X_new, y_pred, "r-")
plt.xlabel("$x$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([-3, 3, 0, 10])
plt.show()A linear model inadequately represents this dataset.
Machine Learning Engineering
- Machine Learning Engineering by Andriy Burkov (A. Burkov 2020).
- Covers data collection, storage, preprocessing, feature engineering, model testing and debugging, deployment, retirement, and maintenance.
- From the author of The Hundred-Page Machine Learning Book (Andriy Burkov 2019).
- Available under a “read first, buy later” model.
PolynomialFeatures
Generate a new feature matrix consisting of all polynomial combinations of the features with degree less than or equal to the specified degree. For example, if an input sample is two dimensional and of the form \([a, b]\), the degree-2 polynomial features are \([1, a, b, a^2, ab, b^2]\).
PolynomialFeatures
Given two features \(a\) and \(b\), PolynomialFeatures with degree=3 would add \(a^2\), \(a^3\), \(b^2\), \(b^3\), as well as, \(ab\), \(a^2b\), \(ab^2\)!
Warning
PolynomialFeatures(degree=d) adds \(\frac{(D+d)!}{d!D!}\) features, where \(D\) is the original number of features.
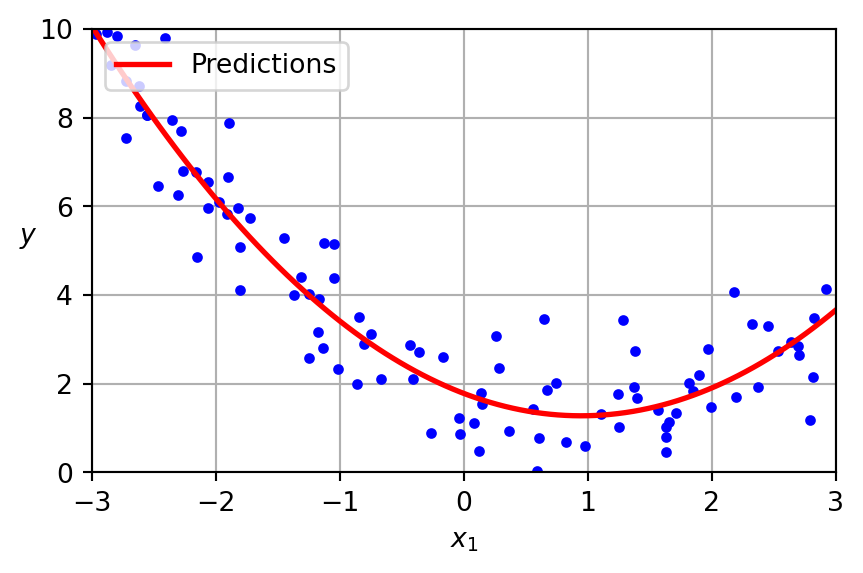
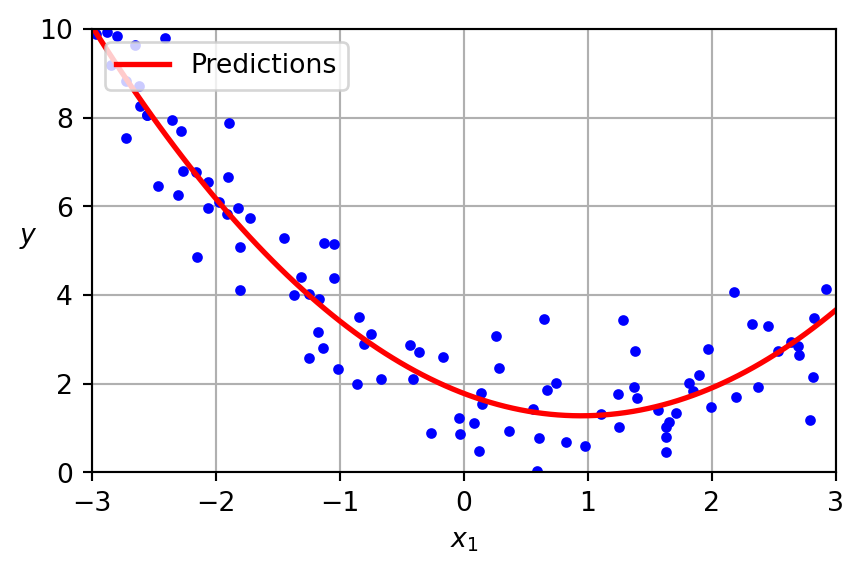
Polynomial Regression
Code
lin_reg = LinearRegression()
lin_reg = lin_reg.fit(X_poly, y)
X_new = np.linspace(-3, 3, 100).reshape(100, 1)
X_new_poly = poly_features.transform(X_new)
y_new = lin_reg.predict(X_new_poly)
plt.figure(figsize=(5, 3))
plt.plot(X, y, "b.")
plt.plot(X_new, y_new, "r-", linewidth=2, label="Predictions")
plt.xlabel("$x_1$")
plt.ylabel("$y$", rotation=0)
plt.legend(loc="upper left")
plt.axis([-3, 3, 0, 10])
plt.grid()
plt.show()LinearRegression on PolynomialFeatures
Polynomial Regression
The data was generated according to the following equation, with the inclusion of Gaussian noise.
\[ y = 0.5 x^2 - 1.0 x + 2.0 \]
Presented below is the learned model.
\[ \hat{y} = 0.56 x^2 + (-1.06) x + 1.78 \]
Data
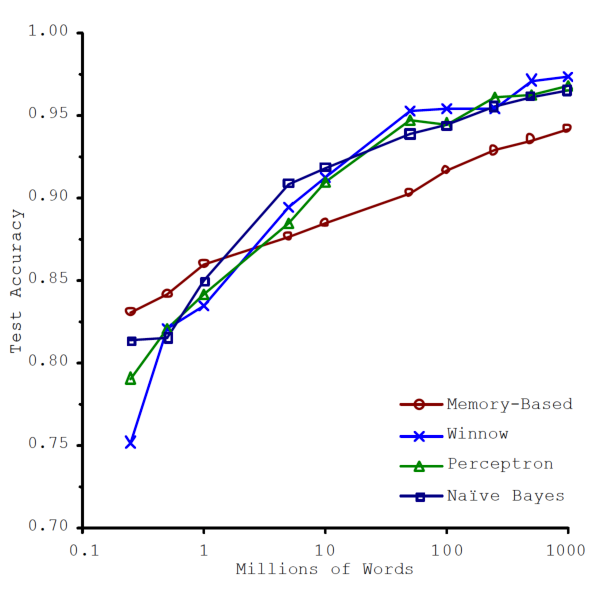
Size does matter
Unreasonable Effectiveness of Data
Definition
Data augmentation is a technique used to increase the diversity of a dataset by applying various transformations to the existing data.
Data Augmentation
- For Images: Rotations, translations, scaling, flipping, adding noise, etc.
- How to find ancient geoglyphs using machine learning?, Sakai et al. (2024)
- For Text: Synonym replacement, random insertion, deletion, and swapping of words.
Prologue
Further readings
- Machine Learning Engineering by Andriy Burkov (A. Burkov 2020).
- Covers data collection, storage, preprocessing, feature engineering, model testing and debugging, deployment, retirement, and maintenance.
- From the author of The Hundred-Page Machine Learning Book (Andriy Burkov 2019).
- Available under a “read first, buy later” model.
Summary
- Attribute Encoding: Evaluation of techniques to avoid bias and possibly speed up the training.
- Preprocessing:
- Data Scaling
- Handling Missing Values
- Managing Class Imbalance
- Training Set Size: Impact on model efficacy and generalization.
Next lecture
- We will introduce artificial neural networks.
References
Appendix: Pipeline
Pipeline
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
num_pipeline = Pipeline([
('imputer', SimpleImputer(strategy="median")),
('attribs_adder', CombinedAttributesAdder()),
('std_scaler', StandardScaler()),
])
training_num_tr = num_pipeline.fit_transform(training_num)
full_pipeline = ColumnTransformer([
("num", num_pipeline, num_attribs),
("cat", OneHotEncoder(), ["sequence"]),
])
training_prepared = full_pipeline.fit_transform(training)Marcel Turcotte
School of Electrical Engineering and Computer Science (EECS)
University of Ottawa
GPT-4o interactions 2024-09-30
I presented GPT-4o with an image of the main character from Marcel the Shell With Shoes On and had the following interactions.
Marcel: How would you describe the subject of the image, its artistic quality, technique, and rendering style?
GPT-4o: The image depicts a whimsical character that resembles a small shell with one large, expressive eye. It stands on two legs wearing shoes, giving it a cute and almost anthropomorphic appearance. The character has a surreal and quirky look, which lends it a sense of personality and charm.
Artistic Quality:
The image is rendered with a high degree of polish and smoothness, possibly created digitally. The textures, shading, and lighting are soft and subtle, giving the character a smooth and rounded look. The rendering captures a delicate balance between realism (in the textures of the shell and shoes) and cartoon-like abstraction (in the exaggerated eye and small stature).
Technique:
The artist appears to have employed a blend of digital painting and 3D-like modeling techniques, with careful attention to detail in the reflections in the eye and the textures of the shell and shoes. The color palette is muted, using soft tones that evoke a gentle, friendly atmosphere.
Rendering Style:
The rendering style is a mix of minimalist and hyperrealist elements. The minimalism is seen in the simplified forms of the character—particularly the body and legs—while the hyperrealism comes through in the detailing of the eye and the subtle textures. This gives the character a tactile, almost tangible quality while maintaining its fantastical, imaginative essence.
The overall effect of the design is both charming and surreal, combining everyday objects (a shell, shoes) with anthropomorphic and fantastical elements to create a unique, playful character.
Marcel: Create an image based on the following description: The image depicts a whimsical character that resembles a small shell with one large, expressive eye. It stands on two legs wearing shoes, giving it a cute and almost anthropomorphic appearance. The character has a surreal and quirky look, which lends it a sense of personality and charm.
Artistic Quality:
The image is rendered with a high degree of polish and smoothness, possibly created digitally. The textures, shading, and lighting are soft and subtle, giving the character a smooth and rounded look. The rendering captures a delicate balance between realism (in the textures of the shell and shoes) and cartoon-like abstraction (in the exaggerated eye and small stature).
Technique:
The artist appears to have employed a blend of digital painting and 3D-like modeling techniques, with careful attention to detail in the reflections in the eye and the textures of the shell and shoes. The color palette is muted, using soft tones that evoke a gentle, friendly atmosphere.
Rendering Style:
The rendering style is a mix of minimalist and hyperrealist elements. The minimalism is seen in the simplified forms of the character—particularly the body and legs—while the hyperrealism comes through in the detailing of the eye and the subtle textures. This gives the character a tactile, almost tangible quality while maintaining its fantastical, imaginative essence.
The overall effect of the design is both charming and surreal, combining everyday objects (a shell, shoes) with anthropomorphic and fantastical elements to create a unique, playful character.
GTP-4o: Here is the image based on the description you provided. Let me know if you’d like to make any adjustments!