Training Artificial Neural Networks (Part 2)

CSI 4106 - Fall 2025

Marcel Turcotte

Version: Oct 22, 2025 07:26

Preamble

Message of the Day

Despite the fact that relatively few students might contemplate a research career, particularly in bioinformatics, the article effectively communicates several key messages. Notably, it is interesting to note that even individuals holding a Ph.D. may feel threatened by the advent of artificial intelligence. The article further illustrates how AI is not eliminating jobs but rather transforming them. In many fields, this transformation redefines roles to those of oversight and supervision.

‘Am I redundant?’: how AI changed my career in bioinformatics, Nature News, 2025-10-13.

Learning objectives

• Backpropagation Algorithm:
  • Discuss the forward and backward passes, highlighting the calculation of gradients using partial derivatives to update weights.
• Vanishing Gradient Problem:
  • Outline the issue and present mitigation strategies, such as using activation functions like ReLU or initializing weights with careful consideration.
• Softmax Layer:
  • Describe its functionality in converting logits into probability distributions for classification tasks.
• Cross-Entropy Loss:
  • Explain its role in measuring the dissimilarity between predicted and true probability distributions.
• Regularization Techniques:
  • Explore methods like L1, L2 regularization, and dropout to enhance neural networks’ generalization capabilities.

In the previous lecture, we implemented a feed-forward neural network to illustrate its functionality. To isolate our conceptual understanding of neural networks from their training methods, we employed a basic brute-force training algorithm. Today, we will focus on the back-propagation algorithm, a critical element in deep learning techniques.

Back-propagation

Attribution : xkcd.com/1838

Back-propagation

Learning representations by back-propagating errors

David E. Rumelhart, Geoffrey E. Hinton & Ronald J. Williams

We describe a new learning procedure, back-propagation, for networks of neurone-like units. The procedure repeatedly adjusts the weights of the connections in the network so as to minimize a measure of the difference between the actual output vector of the net and the desired output vector. As a result of the weight adjustments, internal ‘hidden’ units which are not part of the input or output come to represent important features of the task domain, and the regularities in the task are captured by the interactions of these units. The ability to create useful new features distinguishes back-propagation from earlier, simpler methods such as the perceptron-convergence procedure.

I am presenting here the abstract from the seminal Nature publication where Hinton and colleagues introduced the backpropagation algorithm. This abstract is both elegant and informative, effectively capturing the core principles of modern neural networks: the concept of a loss function, the iterative adjustment of weights through the gradient descent algorithm, and the critical role of hidden layers in generating useful task-dependent features.

Nature is a prestigious journal, and it only occasionally publishes content related to computer science.

At the time of this publication, Hinton was affiliated with Carnegie Mellon University. As a reminder, Hinton received the Nobel Prize in Physics in 2024 for his contributions to developing foundational methods in modern machine learning.

The abstract highlights the rationale for using hidden layers in neural networks. The initial hidden layers learn simple representations directly from the input data, while subsequent layers identify associations among these representations. Each layer builds upon the knowledge of previous layers, culminating in the network’s final output.

Rumelhart, Hinton, and Williams (1986)

Before the back-propagation

• Limitations, such as the inability to solve the XOR classification task, essentially stalled research on neural networks.

• The perceptron was limited to a single layer, and there was no known method for training a multi-layer perceptron.

• Single-layer perceptrons are limited to solving classification tasks that are linearly separable.

Back-propagation: contributions

• The model employs mean squared error as its loss function.

• Gradient descent is used to minimize loss.

• A sigmoid activation function is used instead of a step function, as its derivative provides valuable information for gradient descent.

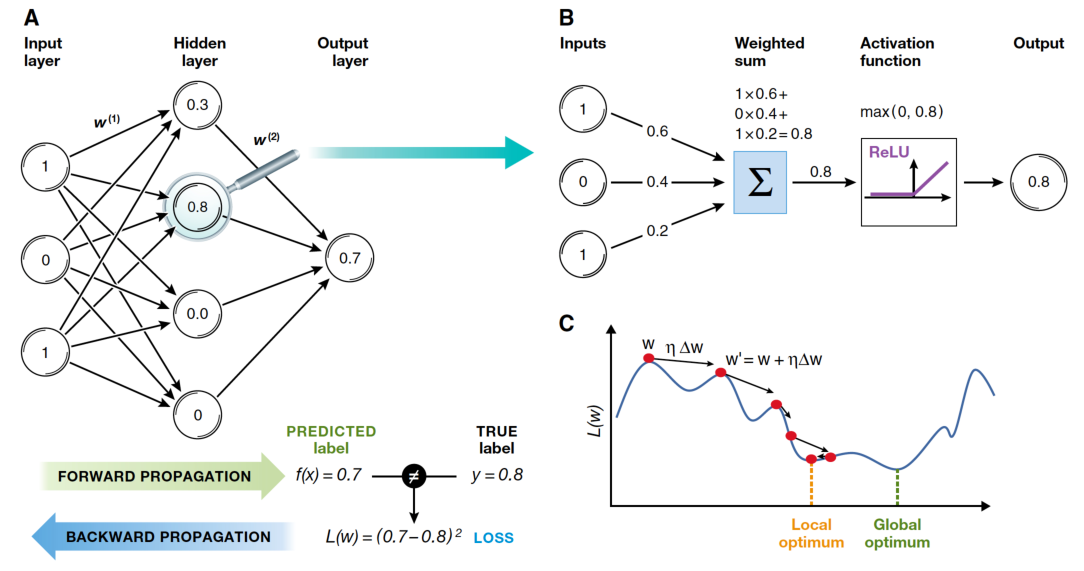
• Shows how updating internal weights using a two-pass algorithm consisting of a forward pass and a backward pass.

• Enables training multi-layer perceptrons.

Conceptual Idea

Given a network and parameters that have been initialized randomly, we can generate predictions (\(\hat{y_i}\)); however, for any non-trivial task, these initial predictions are likely to be inaccurate due to the random nature of the parameter initialization.

In the context of a binary classification problem, what level of accuracy might one anticipate?

Correctly, one would anticipate an accuracy of approximately 50%, assuming the dataset is balanced.

To evaluate the model’s performance, we use a loss function, here the binary cross-entropy (also known as negative log likelihood). This loss function aggregates the loss across all training examples, with the inner term of the summation calculating the loss for each individual example.

In the calculation of the loss, \(\hat{y_i} = h(x_i) = \phi_k( \ldots \phi_2(\phi_1(x)) \ldots )\), where \(\phi_l(Z) = \phi(W_lZ_l + b_l)\) and \(\phi\) without index is an activation function, sigmoid, ReLU, etc.

\(J(\theta) = - \sum_{i=1}^{N} \left[ y_i \log \hat{y_i} + (1-y_i) \log (1 - \hat{y_i}) \right]\)

Conceptual Idea (continued)

In this notation, the index l denotes the processing layers within the model. The index i refers to the individual units within the preceding layer, denoted as l-1, while the index j corresponds to the units within the current layer l.

How many parameters are present in the model?

The model consists of three weight matrices. The dimensions of these matrices are \(2 \times 4\), \(4 \times 4\), and \(4 \times 1\), containing 8, 16, and 4 weights, respectively. This results in a total of 28 weight parameters.

Additionally, there are three arrays for bias terms, containing 4, 4, and 1 biases, respectively, summing up to 9 bias parameters.

Overall, the model comprises 37 parameters, which is relatively small in comparison to more complex models. For instance, the Keras model discussed in the previous lecture had 266,610 parameters. In contemporary machine learning, it is not uncommon for models to contain millions or even billions of parameters.

\(\frac {\partial}{\partial \theta_k}J(\theta)\), for all \(k\), where the \(\theta_k\) are W[l][i,j] and b[l][j].

Conceptual Idea (continued)

Alternative stopping criteria are frequently employed in training algorithms. For example, the process may halt once the training loss reaches a sufficiently low threshold or when the validation loss has increased over a predefined number of epochs.

Model parameters are updated simultaneously, and these updates can be efficiently computed in parallel.

This process is known as gradient descent. As previously discussed, when parameter updates are performed using the entire dataset, the method is referred to as batch gradient descent. Conversely, when updates are made using a single training example, it is termed stochastic gradient descent. Finally, when a small subset of examples, known as a mini-batch, is used for parameter updates, the method is called mini-batch gradient descent.

Our current task involves determining the partial derivatives of the loss function with respect to each of the 37 parameters of our model.

For a fixed number of epochs: \(\theta = \theta - \alpha \nabla_\theta J(\theta)\)

Backpropagation

• Backpropagation is an algorithm for methodically computing the partial derivatives of a neural network’s loss function with respect to each weight and bias parameter.

• Backpropagation applies the chain rule of calculus recursively to compute \(\frac{\partial J}{\partial w_{i,j}^{(\ell)}}\) for all network parameters \(w_{i,j}^{(\ell)}\) efficiently, using intermediate quantities from the forward pass, where \(w_{i,j}^{(\ell)}\) denotes the parameter \(w_{i,j}\) of the layer \(\ell\).

Chain rule

Given,

\[ h(x) = f(g(x)) \]

using the Lagrange notation, we have

\[ h^\prime(x) = f^\prime(g(x)) g^\prime(x) \]

or equivalently using Leibniz notation

\[ \frac{dz}{dx} = \frac{dz}{dy} \cdot \frac{dy}{dx} \]

The chain rule is a fundamental concept in calculus used to determine the derivative of a composite function. Specifically, if a function \(h\) is defined as the composition of two differentiable functions, \(f\) and \(g\), the chain rule provides a method to compute \(h^\prime\).

Conceptually, the chain rule asserts that if you know the instantaneous rate of change of \(z\) with respect to \(y\), and the rate of change of \(y\) with respect to \(x\), you can find the rate of change of \(z\) with respect to \(x\). This is achieved by multiplying these two rates of change.

You now see the connection with compact layer notation, \(\hat{y} = \phi_k( \ldots \phi_2(\phi_1(X)) \ldots )\) where \(\phi_l(Z) = \phi(W_lZ_l + b_l)\), introduced in the last lecture.

Applying the chain rule recursively

Backpropagation simplifies the computational process by decomposing it into a series of elementary steps, where the chain rule is meticulously applied at each stage.

Consider a function depicted by a pink box, parameterized by \(u\), which produces an output \(z\). This output \(z\) serves as the input to another function, eventually culminating in an input to the loss function \(J\).

The expression \(\frac{\partial J}{\partial u}\) denotes the partial derivative of \(J\) with respect to \(u\). This derivative quantifies the sensitivity of the loss \(J\) to changes in the parameter \(u\), indicating whether \(u\) should be increased or decreased, and by what magnitude, to minimize the loss.

According to the chain rule, if \(\frac{\partial J}{\partial z}\) is already known, then \(\frac{\partial J}{\partial u}\) can be computed as \(\frac{\partial z}{\partial u} \cdot \frac{\partial J}{\partial z}\).

Where \(u\) is a parameter of the model, one of those \(w_{i,j}^{(\ell)}\) and \(b_{j}^{(\ell)}\).

Computational graph

The network depicted on the right is more general compared to the one on the left. On the right, \(x\) is a vector, and the pink boxes denote operations on vectors. Consequently, each layer can accommodate an arbitrarily large number of units.

\(W^{(l)}\) refers to the weight matrices, \(b^{(l)}\) to the bias vectors, \(z^{(l)}\) to the pre-activation vectors, and \(a^{(l)}\) to the activation vectors, each associated with layer \(l\).

For illustrative purposes, the representation on the right depicts the loss associated with a single example. To compute the loss over the entire training dataset, one must aggregate these individual losses and subsequently divide the sum by the total number of examples, yielding the average loss.

A two-layer perceptron and its associated computational graph.

Scalar input; one hidden node

Let

\[ J = -\Bigl[y \,\log(\hat y) + (1-y)\,\log(1-\hat y)\Bigr] \]

\[ \hat y = a_2 = \sigma(z_2), \quad z_2 = w_2 \cdot a_1 + b_2 \]

\[ a_1 = \sigma(z_1), \quad z_1 = w_1 \cdot x + b_1 \]

The left side presents the equations for a basic neural network with a scalar input, denoted as \(x\), and a single hidden node. Each layer in this network is characterized by one weight, and thus, a simplified notation with a single subscript is used.

Conversely, the right side illustrates the network using vector notation. In this context, \(W^{(\ell)}\) represents the weight matrix for layer \(\ell\). The dimensions of this matrix are defined as \(\text{input} \times \text{output}\), where input refers to the number of activations from the preceding layer, and output indicates the number of nodes in the current layer.

In this discussion, we will concentrate on scalar equations to enhance clarity and simplicity. Although our focus is on scalar forms, the principles extend to the more general case using vector calculus.

Derivatives

\[ \frac{\partial J}{\partial \hat{y}} \]

\[ \frac{\partial \hat{y}}{\partial z_2} \]

\[ \frac{\partial z_2}{\partial w_2}, \quad \frac{\partial z_2}{\partial b_2}, \quad \frac{\partial z_2}{\partial a_1}, \]

\[ \frac{\partial a_1}{\partial z_1}, \]

\[ \frac{\partial z_1}{\partial w_1}, \quad \frac{\partial z_1}{\partial b_1}, \quad \frac{\partial z_1}{\partial x}, \]

Derivatives

Loss derivative w.r.t. \(\hat{y}\):

\[ \frac{\partial J}{\partial \hat{y}} = -\left(\frac{y}{\hat{y}}-\frac{1-y}{1-\hat{y}}\right) \]

Derivatives

\(\hat{y}\) derivative w.r.t. \(z_2\):

\[ \frac{\partial \hat{y}}{\partial z_2}=\sigma^{\prime}\left(z_2\right)=\hat{y}(1-\hat{y}) \]

Derivatives

Derivative \(z_2 = w_2 a_1 + b_2\):

\[ \frac{\partial z_2}{\partial w_2}=a_1, \quad \frac{\partial z_2}{\partial b_2}=1, \quad \frac{\partial z_2}{\partial a_1}=w_2 \]

Derivatives

Derivative \(a_1 = \sigma(z_1)\):

\[ \frac{\partial a_1}{\partial z_1}=\sigma^{\prime}\left(z_1\right)=a_1\left(1-a_1\right) \]

Derivatives

Derivative \(z_1 = w_1 x + b_1\):

\[ \frac{\partial z_1}{\partial w_1}=x, \quad \frac{\partial z_1}{\partial b_1}=1, \quad \frac{\partial z_1}{\partial x} = w_1 \]

Combined derivatives

For \(w_2\):

\[ \frac{\partial J}{\partial w_2}=\frac{\partial J}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial z_2} \cdot \frac{\partial z_2}{\partial w_2}=\left[-\left(\frac{y}{\hat{y}}-\frac{1-y}{1-\hat{y}}\right)\right] \cdot(\hat{y}(1-\hat{y})) \cdot a_1 \]

Simplifies to:

\[ \frac{\partial J}{\partial w_2}=(\hat{y}-y) a_1 \]

Combined derivatives

For \(b_2\):

\[ \frac{\partial J}{\partial b_2}=\frac{\partial J}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial z_2} \cdot \frac{\partial z_2}{\partial b_2}=(\hat{y}-y) \cdot 1=\hat{y}-y \]

Combined derivatives

For \(w_1\):

\[ \frac{\partial J}{\partial w_1}=\frac{\partial J}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial z_2} \cdot \frac{\partial z_2}{\partial a_1} \cdot \frac{\partial a_1}{\partial z_1} \cdot \frac{\partial z_1}{\partial w_1} \]

Plug in:

\[ =\left[-\left(\frac{y}{\hat{y}}-\frac{1-y}{1-\hat{y}}\right)\right] \cdot(\hat{y}(1-\hat{y})) \cdot w_2 \cdot\left(a_1\left(1-a_1\right)\right) \cdot x \]

Simplifies to:

\[ \frac{\partial J}{\partial w_1}=(\hat{y}-y) w_2\left(a_1\left(1-a_1\right)\right) x \]

Combined derivatives

For \(b_1\):

\[ \frac{\partial J}{\partial b_1}=\frac{\partial J}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial z_2} \cdot \frac{\partial z_2}{\partial a_1} \cdot \frac{\partial a_1}{\partial z_1} \cdot \frac{\partial z_1}{\partial b_1} \]

Plug in:

\[ =(\hat{y}-y) w_2\left(a_1\left(1-a_1\right)\right) \cdot 1 \]

Simplifies to:

\[ \frac{\partial J}{\partial b_1}=(\hat{y}-y) w_2\left(a_1\left(1-a_1\right)\right) \]

Key derivatives

\[ \begin{align} \frac{\partial J}{\partial w_2} & = (\hat{y}-y) a_1 \\ \frac{\partial J}{\partial b_2} & = \hat{y}-y \\ \frac{\partial J}{\partial w_1} & = (\hat{y}-y) w_2\left(a_1\left(1-a_1\right)\right) x \\ \frac{\partial J}{\partial b_1} & = (\hat{y}-y) w_2\left(a_1\left(1-a_1\right)\right) \\ \end{align} \]

Observation 1: The computation of key gradients necessitates the activation values from all layers, specifically \(a_1\) and \(\hat{y} = a_2\).

Exploration

import math
import random

random.seed(42)

def sigma(x):
    return 1 / (1 + math.exp(-x))

alpha = 0.1

def init():

    global w1, w2, b1, b2

    w1 = random.random()
    w2 = random.random()
    b1 = 0
    b2 = 0

We consider a straightforward neural network model. It accepts a single scalar input, denoted as \(x\), and comprises a single hidden node characterized by a weight \(w_1\) and bias \(b_1\). It also includes an output node with a weight \(w_2\) and bias \(b_2\). In total, the network contains four trainable parameters.

Forward

def forward():

    global z1, w1, x, b1, a1, z2, J, y_hat

    z1 = w1 * x + b1
    a1 = sigma(z1)

    z2 = w2 * a1 + b2
    a2 = sigma(z2)

    y_hat = a2

    J = -(y * math.log(y_hat) + (1-y) * math.log(1 - y_hat))

In the forward pass, the computations progress sequentially through each layer, calculating both preactivation and activation values, denoted as z1, a1, z2, and a2. The value a2 represents the model’s output, which is subsequently utilized to determine the loss.

Backward

def backward():

    global alpha, w1, b1, w2, b2, a1, z1, z2, y, y_hat

    grad_J_w2 = (y_hat - y) * a1
    grad_J_b2 = y_hat - y

    grad_J_w1 = (y_hat - y) * w2 * (a1 * (1-a1)) * x
    grad_J_b1 = (y_hat - y) * w2 * (a1 * (1-a1))

    w2 = w2 - alpha * grad_J_w2
    b2 = b2 - alpha * grad_J_b2

    w1 = w1 - alpha * grad_J_w1
    b1 = b1 - alpha * grad_J_b1

During the backward pass, the partial derivatives, or gradients, are calculated for each of the four parameters. Subsequently, these gradients are utilized to update the corresponding weights through a process known as gradient updating.

Training

init()

x = 3.14
y = 1

forward()
print(f"Before: y_hat = {y_hat:.2}, loss = {J:.2}")

for i in range(500):
    forward()
    backward()

forward()
print(f"After: y_hat = {y_hat:.2}, loss = {J:.2}")

Before: y_hat = 0.51, loss = 0.68
After: y_hat = 0.99, loss = 0.01

The training process we have implemented is based on a single data instance. As it stands, our basic network architecture is restricted to processing only this one example, primarily due to the hard-coded nature of the loss function, which is specifically tailored for a single input. However, you can experiment with various parameters to observe their effects on the model’s performance. These parameters include setting y=0, adjusting the input value x, modifying the learning rate alpha, or altering the number of training epochs.

Key derivatives

\[ \begin{align} \frac{\partial J}{\partial w_2} & = \frac{\partial J}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial z_2} \cdot \frac{\partial z_2}{\partial w_2}\\ \frac{\partial J}{\partial b_2} & = \frac{\partial J}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial z_2} \cdot \frac{\partial z_2}{\partial b_2}\\ \frac{\partial J}{\partial w_1} & = \frac{\partial J}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial z_2} \cdot \frac{\partial z_2}{\partial a_1} \cdot \frac{\partial a_1}{\partial z_1} \cdot \frac{\partial z_1}{\partial w_1}\\ \frac{\partial J}{\partial b_1} & = \frac{\partial J}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial z_2} \cdot \frac{\partial z_2}{\partial a_1} \cdot \frac{\partial a_1}{\partial z_1} \cdot \frac{\partial z_1}{\partial b_1}\\ \end{align} \]

It is harly surprising, given that these chains follow the same path within the computational graph.

Observation 2: Notice how some derivatives, such as \(\frac{\partial J}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial z_2}\), are computed multiple times.

Key derivatives

Let \[ \begin{align} \delta_1 & = \frac{\partial J}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial z_2} \\ \delta_2 & = \delta_1 \cdot \frac{\partial z_2}{\partial a_1} \cdot \frac{\partial a_1}{\partial z_1} \end{align} \]

Rewrite \[ \begin{align} \frac{\partial J}{\partial w_2} & = \delta_1 \cdot \frac{\partial z_2}{\partial w_2}\\ \frac{\partial J}{\partial b_2} & = \delta_1 \cdot \frac{\partial z_2}{\partial b_2}\\ \frac{\partial J}{\partial w_1} & = \delta_2 \cdot \frac{\partial z_1}{\partial w_1}\\ \frac{\partial J}{\partial b_1} & = \delta_2 \cdot \frac{\partial z_1}{\partial b_1}\\ \end{align} \]

In our initial discussion, we combined and simplified the partial derivatives. To streamline this process, we can extend the chain rule by multiplying the local derivative with the precomputed partial derivative that traces the path from the output layer to the local processing unit within the computational graph. This approach not only simplifies the process but also facilitates automation.

In the presentation, we simplified the network model by using a single scalar input and two processing units, each equipped with an individual weight and bias. For the purpose of demonstration, we trained this model with a single example. Expanding the model to include additional inputs and processing nodes transforms the weights (\(w\)) into matrices and the biases (\(b\)) into vectors, while the underlying mechanics transition to vector calculus. Similarly, incorporating more layers into the network does not inherently increase the algorithm’s complexity. It merely extends the backpropagation loop, as the operations for each layer remain consistent. In fact, our computational graph representation is already expressed using vector notation.

In backpropagation, the process progresses from the output layer towards the input layer, systematically calculating and storing intermediate partial derivatives.

Backpropagation: top level

1. (Computational Graph Creation)

2. Initialization

3. Forward Pass

4. Compute Loss

5. Backward Pass (Backpropagation)

6. Update the parameters and repeat 3 to 6.

Modern frameworks like TensorFlow and PyTorch build a computational graph to represent the operations and data flow within a neural network. In contrast, our simplified implementation will not utilize this approach.

The algorithm stops either after a predefined number of epochs or when convergence criteria are satisfied.

Backpropagation: detailed

1. (Create the computational graph.)

2. Initialize the weights and biases.

3. Forward pass: starting from the input, compute the output of each operation in the graph, and store these values.

4. Compute loss.

5. Backward pass: starting from the output and moving backward, for each operation.

   1. Compute the derivative of the output with respect to each of the inputs.

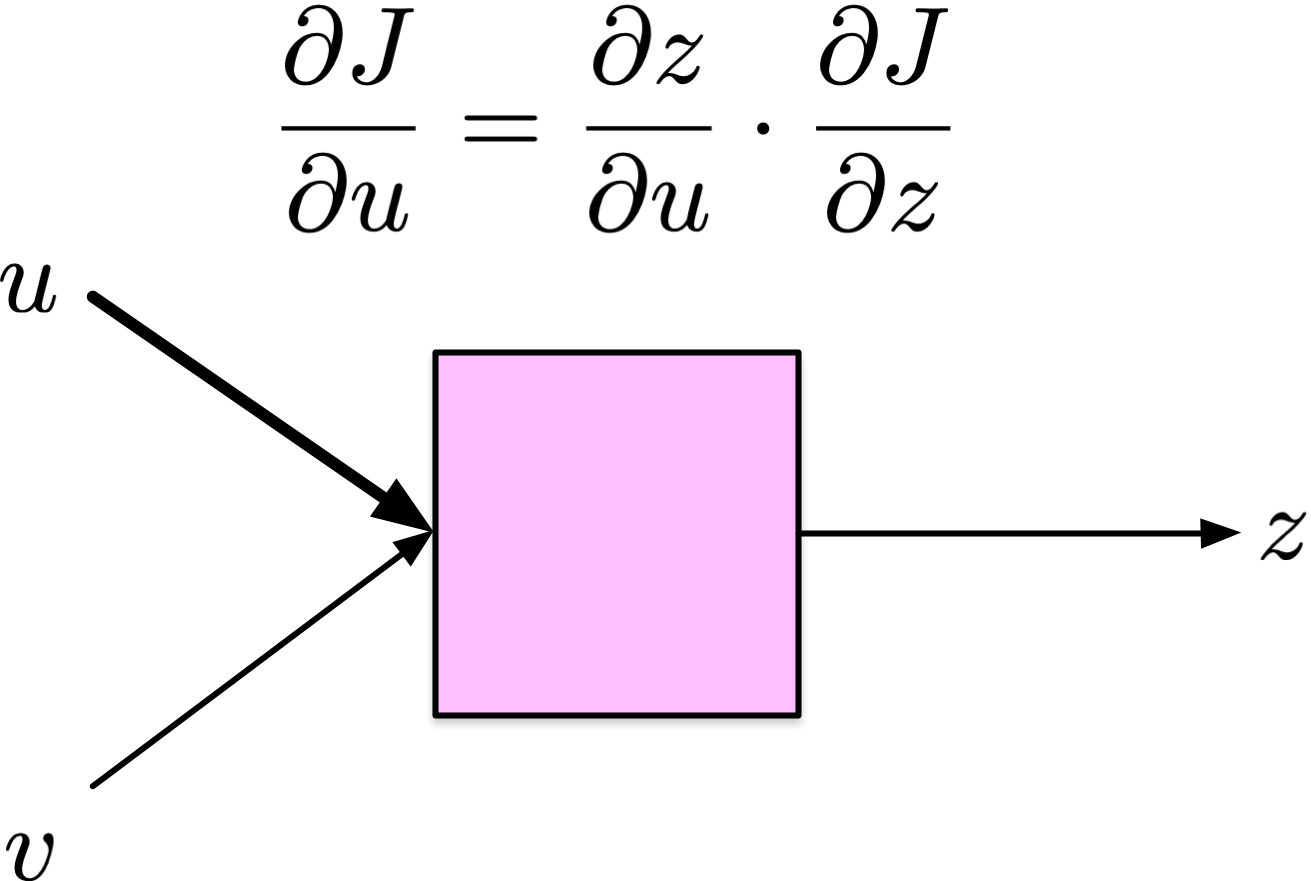
   2. For each input \(u\),

\[ \delta_u = \frac{\partial J}{\partial u} = \frac{\partial z}{\partial u} \cdot \frac{\partial J}{\partial z} \]

6. Update the parameters and repeat 3 to 6.

Backpropagation: 2. Initialization

Initialize the weights and biases of the neural network.

1. Zero Initialization
   • All weights are initialized to zero.
   • Symmetry problems, all neurons produce identical outputs, preventing effective learning.
2. Random Initialization
   • Weights are initialized randomly, often using a uniform or normal distribution.
   • Breaks the symmetry between neurons, allowing them to learn.
   • If not scaled properly, leads to slow convergence or vanishing/exploding gradients.

Initializing weights and biases to zero works for logistic regression because it is a linear model with a single layer. In logistic regression, each feature’s weight is independently adjusted during training, and the optimization process can converge correctly regardless of the initial weights, provided the data is linearly separable.

However, zero initialization does not work well for neural networks due to their multi-layered structure. Here’s why:

1. Symmetry Breaking: Neural networks require breaking symmetry between neurons in each layer so that they can learn different features. If all weights are initialized to zero, each neuron in a layer will compute the same output and receive the same gradient during backpropagation. This results in the neurons updating identically, preventing them from learning distinct features and effectively rendering multiple neurons redundant.

2. Non-Linearity: Neural networks rely on non-linear transformations between layers to model complex relationships in the data. Zero initialization inhibits the ability of neurons to activate differently, impeding the network’s capacity to capture non-linear patterns.

See also: Xavier/Glorot and He initialization (later)

Backpropagation: 3. Forward Pass

For each example in the training set (or in a mini-batch):

• Input Layer: Pass input features to first layer.

• Hidden Layers: For each hidden layer, compute the activations (output) by applying the weighted sum of inputs plus bias, followed by an activation function (e.g., sigmoid, ReLU).

• Output Layer: Same process as hidden layers. Output layer activations represent the predicted values.

In practice, it is the mini-batch version of this algorithm that is being used. Stochastic gradient descent is a special case of mini-batch gradient descent where the mini-batch size is one.

The forward pass is almost identical to applying the network for prediction (.predict()), with the exception that intermediate (activation) results are saved, as they are needed for the backward pass.

Backpropagation: 4. Compute Loss

Calculate the loss (error) using a suitable loss function by comparing the predicted values to the actual target values.

A smaller loss indicates that the predicted values are closer to the actual target values.

The value of the loss function can serve as a stopping criterion, with backpropagation halting when the loss is sufficiently small.

Crucially, the derivative of the loss function provides essential information for adjusting the network’s weights and bias terms.

More on the various loss functions coming later: mean squared error for regression tasks or cross-entropy loss for classification tasks.

Backpropagation: 5. Backward Pass

• Output Layer: Compute the gradient of the loss with respect to the output layer’s weights and biases using the chain rule of calculus.

• Hidden Layers: Propagate the error backward through the network, layer by layer. For each layer, compute the gradient of the loss with respect to the weights and biases. Use the derivative of the activation function to help calculate these gradients.

• Update Weights and Biases: Adjust the weights and biases using the calculated gradients and a learning rate, which determines the step size for each update.

At the end of the presentation, links are provided to a series of videos by Herman Kamper. These videos elucidate the intricacies of the backpropagation algorithm across various architectures, both with and without forks, utilizing function composition and graph computation approaches.

While the algorithm is complex due to the numerous cases it entails, its regular structure makes it suitable for automation. Specifically, algorithms like automatic differentiation (autodiff) facilitate this process.

In 1970, Seppo Ilmari Linnainmaa introduced the algorithm known as reverse mode automatic differentiation in his MSc thesis. Although he did not apply this algorithm to neural networks, it is more general than backpropagation.

Common optimization techniques like gradient descent or its variants (e.g., Adam) are employed.

Backpropagation - Purpose

• Algorithm to train multi-layer perceptrons (MLPs) by minimizing a loss function.
• Enables hidden layers to learn useful internal representations by adjusting weights and biases.

Backpropagation - Core Idea

• Iteratively adjust parameters to reduce the difference between predicted and true outputs.

• Uses gradient descent on the loss function:

  \[ \theta \leftarrow \theta - \alpha \nabla_\theta J(\theta) \]

  where \(\alpha\) is the learning rate.

Backpropagation - Summary

1. Create the computational graph

2. Initialize weights & biases

3. Forward pass: compute activations & loss.

4. Backward pass: compute gradients using chain rule.

5. Update parameters:

   \(W^{(\ell)} \leftarrow W^{(\ell)} - \alpha \frac{\partial J}{\partial W^{(\ell)}}\)

   \(b^{(\ell)} \leftarrow b^{(\ell)} - \alpha \frac{\partial J}{\partial b^{(\ell)}}\)

6. Repeat until convergence.

Implementation

Backpropagation - Forward Pass

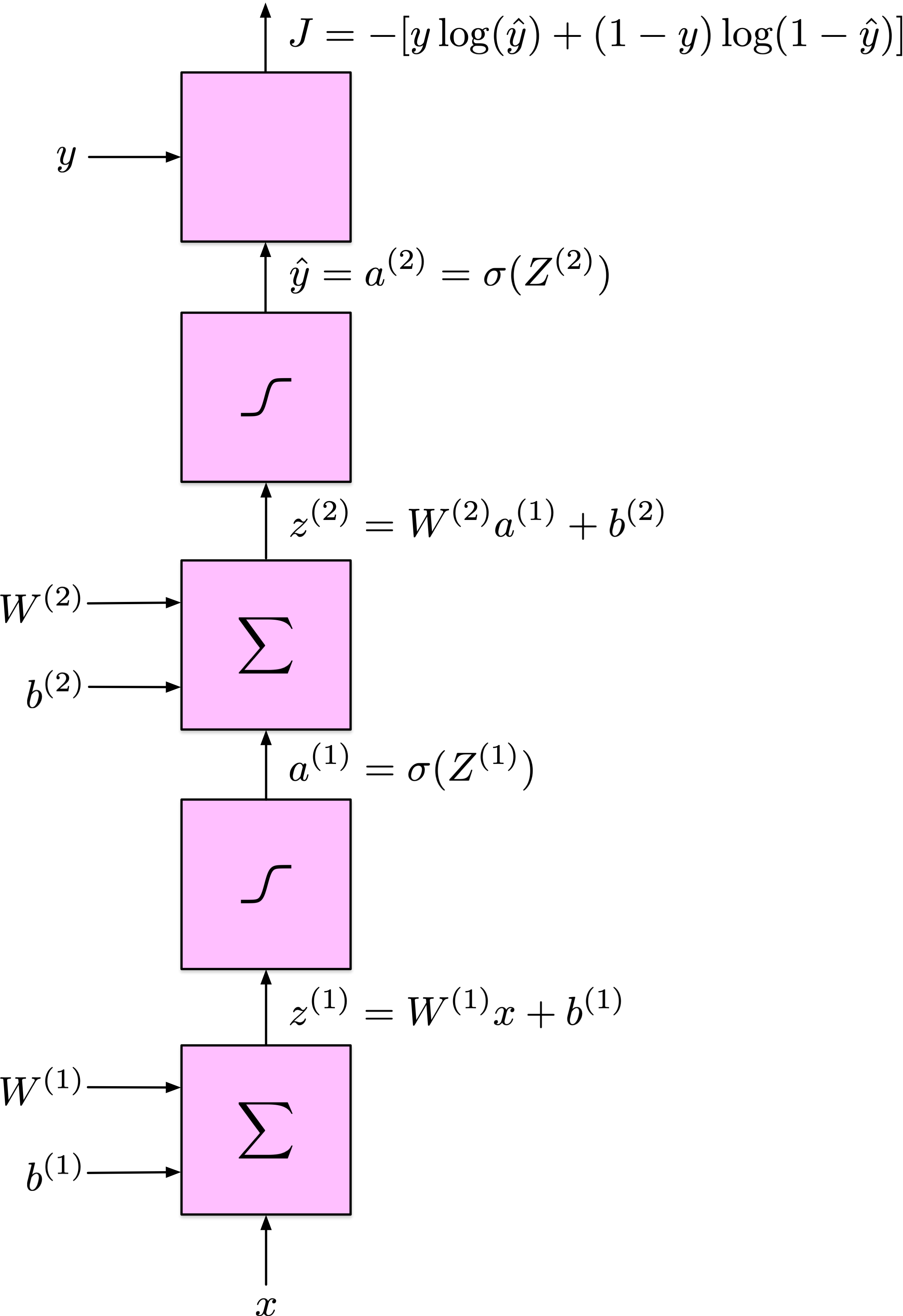
• Compute activations layer by layer:

  \(z^{(\ell)} = W^{(\ell)} a^{(\ell-1)} + b^{(\ell)}\),

  \(a^{(\ell)} = \phi(z^{(\ell)})\).

• Obtain prediction \(\hat{y}\) and compute loss \(J(\hat{y}, y)\).

Backpropagation - Backward Pass

• Apply chain rule to compute partial derivatives of the loss with respect to each parameter efficiently.
• Propagate gradients from output to input layers:

\[ \delta^{(\ell)} = (W^{(\ell+1)} \delta^{(\ell+1)}) \odot \phi'(z^{(\ell)}) \]

• \(\delta^{(\ell)}\) — the error term (or local gradient) for layer \(\ell\), defined as \(\displaystyle \delta^{(\ell)} = \frac{\partial J}{\partial z^{(\ell)}}\), the sensitivity of the loss \(J\) to the preactivation \(z^{(\ell)}\).

• \(\delta^{(\ell+1)}\) — the error term from the next layer (closer to the output). This is already known from the previous step in backpropagation.

• \(W^{(\ell+1)} \delta^{(\ell+1)}\) — propagates the next layer’s error backward through the weights of layer \(\ell+1\). Each neuron in layer \(\ell\) receives a weighted sum of the downstream errors.

• \(\phi'(z^{(\ell)})\) — the derivative of the activation function at layer \(\ell\). It scales the error according to how sensitive the neuron’s activation was to changes in its input.

Where \(\odot\) is the elementwise (Hadamard) product.

SimpleMLP

The complete implementation is presented below and will be examined in the subsequent slides.

import numpy as np

# Activations & loss

def sigmoid(z):
    return 1.0 / (1.0 + np.exp(-z))

def sigmoid_prime(z):
    s = sigmoid(z)
    return s * (1.0 - s)

def relu(z):
    return np.maximum(0.0, z)

def relu_prime(z):
    return (z > 0).astype(z.dtype)

def bce_loss(y_true, y_prob, eps=1e-9):

    """Binary cross-entropy averaged over samples (with clipping for stability)."""

    y_prob = np.clip(y_prob, eps, 1 - eps)
    return -np.mean(y_true * np.log(y_prob) + (1 - y_true) * np.log(1 - y_prob))

# Initializers

def he_init(rng, fan_in, fan_out):

    # He normal: good for ReLU

    std = np.sqrt(2.0 / fan_in)
    return rng.normal(0.0, std, size=(fan_in, fan_out))

def xavier_init(rng, fan_in, fan_out):

    # Glorot/Xavier normal: good for sigmoid/tanh

    std = np.sqrt(2.0 / (fan_in + fan_out))
    return rng.normal(0.0, std, size=(fan_in, fan_out))


# SimpleMLP (API mirrors NaiveMLP)

class SimpleMLP:

    """
    Minimal MLP for binary classification.

    - Hidden: ReLU (default) with He init; or 'sigmoid' with Xavier init
    - Output: Sigmoid + BCE (δ_L = a_L - y)
    - API: forward -> probas (N,), predict_proba, predict, loss, train
    """

    def __init__(self, layer_sizes, lr=0.1, seed=None, l2=0.0,
                 hidden_activation="relu", lr_decay=None):
        """
        layer_sizes: e.g., [2, 4, 4, 1]
        lr: learning rate
        l2: L2 regularization strength (0 disables)
        hidden_activation: 'relu' (default) or 'sigmoid'
        lr_decay: optional float in (0,1); multiply lr by this every epoch (e.g., 0.9)
        """
        self.sizes = list(layer_sizes)
        self.lr = float(lr)
        self.base_lr = float(lr)
        self.lr_decay = lr_decay
        self.l2 = float(l2)
        self.hidden_activation = hidden_activation
        rng = np.random.default_rng(seed)

        # Initialize weights/biases per layer
        self.W = []
        for din, dout in zip(self.sizes[:-1], self.sizes[1:]):
            if hidden_activation == "relu":
                Wk = he_init(rng, din, dout)
            else:
                Wk = xavier_init(rng, din, dout)
            self.W.append(Wk)
        self.b = [np.zeros(dout) for dout in self.sizes[1:]]

    # activations (hidden vs output)

    def _act(self, z, last=False):
        if last:
            return sigmoid(z)  # output layer
        return relu(z) if self.hidden_activation == "relu" else sigmoid(z)

    def _act_prime(self, z, last=False):
        if last:
            return sigmoid_prime(z)  # rarely needed with BCE+sigmoid
        return relu_prime(z) if self.hidden_activation == "relu" else sigmoid_prime(z)

    # forward (public): returns probabilities (N,)

    def forward(self, X):
        a = X
        L = len(self.W)
        for ell, (W, b) in enumerate(zip(self.W, self.b), start=1):
            a = self._act(a @ W + b, last=(ell == L))
        return a.ravel()

    # Aliases to match NaiveMLP

    def predict_proba(self, X):
        return self.forward(X)

    def predict(self, X, threshold=0.5):
        return (self.predict_proba(X) >= threshold).astype(int)

    def loss(self, X, y):

        # BCE + optional L2
        p = self.predict_proba(X)
        base = bce_loss(y, p)
        if self.l2 > 0:
            reg = 0.5 * self.l2 * sum((W**2).sum() for W in self.W)
            # Normalize reg by number of samples to be consistent with mean loss
            base += reg / max(1, X.shape[0])
        return base

    # internal: forward caches for backprop

    def _forward_full(self, X):
        a = X
        activations = [a]
        zs = []
        L = len(self.W)
        for ell, (W, b) in enumerate(zip(self.W, self.b), start=1):
            z = a @ W + b
            a = self._act(z, last=(ell == L))
            zs.append(z)
            activations.append(a)
        return activations, zs

    # training: mini-batch gradient descent with backprop

    def train(self, X, y, epochs=30, batch_size=None, verbose=True, shuffle=True):

        """
        X: (N, d), y: (N,) in {0,1}
        batch_size: None -> full-batch; else int
        """

        N = X.shape[0]
        idx = np.arange(N)
        B = N if batch_size is None else int(batch_size)

        for ep in range(1, epochs + 1):
            if shuffle:
                np.random.shuffle(idx)
            if self.lr_decay:
                self.lr = self.base_lr * (self.lr_decay ** (ep - 1))

            base_loss = self.loss(X, y)

            for start in range(0, N, B):
                sl = idx[start:start+B]
                Xb = X[sl]
                yb = y[sl].reshape(-1, 1)  # (B,1)

                # Forward caches
                activations, zs = self._forward_full(Xb)
                A_L = activations[-1]          # (B,1)
                Bsz = Xb.shape[0]

                # Backprop
                # Output layer: BCE + sigmoid => delta_L = (A_L - y)

                delta = (A_L - yb)             # (B,1)

                grads_W = [None] * len(self.W)
                grads_b = [None] * len(self.b)

                # Last layer grads

                grads_W[-1] = activations[-2].T @ delta / Bsz   # (n_{L-1}, 1)
                grads_b[-1] = delta.mean(axis=0)                # (1,)

                # Hidden layers: l = L-1 down to 1

                for l in range(2, len(self.sizes)):
                    z = zs[-l]                                  # (B, n_l)
                    sp = self._act_prime(z, last=False)         # (B, n_l)
                    delta = (delta @ self.W[-l+1].T) * sp       # (B, n_l)
                    grads_W[-l] = activations[-l-1].T @ delta / Bsz  # (n_{l-1}, n_l)
                    grads_b[-l] = delta.mean(axis=0)                 # (n_l,)

                # L2 regularization (add to grads)

                if self.l2 > 0:
                    for k in range(len(self.W)):
                        grads_W[k] = grads_W[k] + self.l2 * self.W[k]

                # Gradient step

                for k in range(len(self.W)):
                    self.W[k] -= self.lr * grads_W[k]
                    self.b[k] -= self.lr * grads_b[k]

            new_loss = self.loss(X, y)
            if verbose:
                print(f"Epoch {ep:3d} | loss {base_loss:.5f} → {new_loss:.5f} | Δ={base_loss - new_loss:.5f} | lr={self.lr:.4f}")

Activation functions

def sigmoid(z):
    return 1.0 / (1.0 + np.exp(-z))

def sigmoid_prime(z):
    s = sigmoid(z)
    return s * (1.0 - s)

def relu(z):
    return np.maximum(0.0, z)

def relu_prime(z):
    return (z > 0).astype(z.dtype)

As stated in a previous lecture, the derivative of the sigmoid function is conveniently expressed as the product of the sigmoid function itself and one minus the sigmoid function.

We’re including ReLU as well.

Loss

def bce_loss(y_true, y_prob, eps=1e-9):

    """Binary cross-entropy averaged over samples (with clipping for stability)."""

    y_prob = np.clip(y_prob, eps, 1 - eps)

    return -np.mean(y_true * np.log(y_prob) + (1 - y_true) * np.log(1 - y_prob))

Initializers

def he_init(rng, fan_in, fan_out):

    # He normal: good for ReLU

    std = np.sqrt(2.0 / fan_in)
    return rng.normal(0.0, std, size=(fan_in, fan_out))

def xavier_init(rng, fan_in, fan_out):

    # Glorot/Xavier normal: good for sigmoid/tanh

    std = np.sqrt(2.0 / (fan_in + fan_out))
    return rng.normal(0.0, std, size=(fan_in, fan_out))

In the upcoming lecture, we will explore the issue of the vanishing gradient, a common challenge encountered in deep neural networks. One approach to mitigating this problem involves modifying the activation functions and adjusting the weight initialization methods.

Class definition + constructor

class SimpleMLP:

    def __init__(self, layer_sizes, lr=0.1, seed=None, l2=0.0,
                 hidden_activation="relu", lr_decay=None):

        self.sizes = list(layer_sizes)
        self.lr = float(lr)
        self.base_lr = float(lr)
        self.lr_decay = lr_decay
        self.l2 = float(l2)
        self.hidden_activation = hidden_activation
        rng = np.random.default_rng(seed)

        # Initialize weights/biases per layer
        self.W = []
        for din, dout in zip(self.sizes[:-1], self.sizes[1:]):
            if hidden_activation == "relu":
                Wk = he_init(rng, din, dout)
            else:
                Wk = xavier_init(rng, din, dout)
            self.W.append(Wk)
        self.b = [np.zeros(dout) for dout in self.sizes[1:]]

The constructor aligns with that of NaiveMLP, with the key difference being that it retains a learning rate rather than a step value. Additionally, the initialization of weights varies based on the specific activation functions employed.

Forward (public)

    def forward(self, X):
        a = X
        L = len(self.W)
        for ell, (W, b) in enumerate(zip(self.W, self.b), start=1):
            a = self._act(a @ W + b, last=(ell == L))
        return a.ravel()

where _act is defined as follows:

    def _act(self, z, last=False):
        if last:
            return sigmoid(z)  # output layer
        return relu(z) if self.hidden_activation == "relu" else sigmoid(z)

The SimpleMLP model incorporates two distinct implementations of the forward method: one tailored for prediction tasks and the other for model training.

Forward (private)

    def _forward_full(self, X):
        a = X
        activations = [a]
        zs = []
        L = len(self.W)
        for ell, (W, b) in enumerate(zip(self.W, self.b), start=1):
            z = a @ W + b
            a = self._act(z, last=(ell == L))
            zs.append(z)
            activations.append(a)
        return activations, zs

The private method forward differs in that it retains both the preactivation values (zs) and the activation values (activations). This retention is important, as these values are required during the backward propagation phase.

Training

    def train(self, X, y, epochs=30, batch_size=None, verbose=True, shuffle=True):

        """
        X: (N, d), y: (N,) in {0,1}
        batch_size: None -> full-batch; else int
        """

        N = X.shape[0]
        idx = np.arange(N)
        B = N if batch_size is None else int(batch_size)

        for ep in range(1, epochs + 1):
            if shuffle:
                np.random.shuffle(idx)
            if self.lr_decay:
                self.lr = self.base_lr * (self.lr_decay ** (ep - 1))

            base_loss = self.loss(X, y)

            for start in range(0, N, B):
                sl = idx[start:start+B]
                Xb = X[sl]
                yb = y[sl].reshape(-1, 1)  # (B,1)

                # Forward caches
                activations, zs = self._forward_full(Xb)
                A_L = activations[-1]          # (B,1)
                Bsz = Xb.shape[0]

                # Backprop
                # Output layer: BCE + sigmoid => delta_L = (A_L - y)

                delta = (A_L - yb)             # (B,1)

                grads_W = [None] * len(self.W)
                grads_b = [None] * len(self.b)

                # Last layer grads

                grads_W[-1] = activations[-2].T @ delta / Bsz   # (n_{L-1}, 1)
                grads_b[-1] = delta.mean(axis=0)                # (1,)

                # Hidden layers: l = L-1 down to 1

                for l in range(2, len(self.sizes)):
                    z = zs[-l]                                  # (B, n_l)
                    sp = self._act_prime(z, last=False)         # (B, n_l)
                    delta = (delta @ self.W[-l+1].T) * sp       # (B, n_l)
                    grads_W[-l] = activations[-l-1].T @ delta / Bsz  # (n_{l-1}, n_l)
                    grads_b[-l] = delta.mean(axis=0)                 # (n_l,)

                # L2 regularization (add to grads)

                if self.l2 > 0:
                    for k in range(len(self.W)):
                        grads_W[k] = grads_W[k] + self.l2 * self.W[k]

                # Gradient step

                for k in range(len(self.W)):
                    self.W[k] -= self.lr * grads_W[k]
                    self.b[k] -= self.lr * grads_b[k]

            new_loss = self.loss(X, y)
            if verbose:
                print(f"Epoch {ep:3d} | loss {base_loss:.5f} → {new_loss:.5f} | Δ={base_loss - new_loss:.5f} | lr={self.lr:.4f}")

Our implementation successfully replicates several key features of contemporary frameworks. It provides options to define the batch size and to decide whether to shuffle the data.

In general, you should shuffle the data before (and usually at the start of every epoch during) neural network training.

1. Breaks ordering bias: If the dataset has any underlying order (e.g., sorted by class, time, or difficulty), training sequentially could make the model overfit early batches and generalize poorly.

2. Improves stochasticity: Shuffling ensures each mini-batch provides a representative mix of the data distribution, stabilizing the stochastic gradient descent (SGD) updates and improving convergence.

3. Prevents periodic patterns: Without shuffling, the optimizer might see similar samples repeatedly in the same order, leading to oscillations or slower convergence.

Exception:

• Time-series or sequential data:

  If the order carries meaning (temporal or causal structure), do not shuffle across time.

Our method incorporates a dynamic training schedule that progressively reduces the learning rate as the number of training epochs increases.

Testing

from sklearn.preprocessing import StandardScaler
from sklearn.datasets import make_circles
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

X, y = make_circles(n_samples=200, factor=0.5, noise=0.08, random_state=1)

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0, stratify=y)

scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

model = SimpleMLP([2, 4, 4, 1], lr=0.3, seed=42, hidden_activation="relu", l2=0.0, lr_decay=0.95)

model.train(X_train, y_train, epochs=150, batch_size=32, verbose=False)

print("Train acc:", accuracy_score(y_train, model.predict(X_train)))
print(" Test acc:", accuracy_score(y_test, model.predict(X_test)))

Train acc: 0.9428571428571428
 Test acc: 0.9166666666666666

Automatic differentiation

Automatic differentiation (autodiff) systematically applies the chain rule to compute exact derivatives of functions expressed as computer programs. It propagates derivatives through elementary operations, either forward (from inputs to outputs) or backward (from outputs to inputs), enabling efficient and precise gradient computation essential for optimization and learning algorithms.

Baydin et al. (2017)

Training

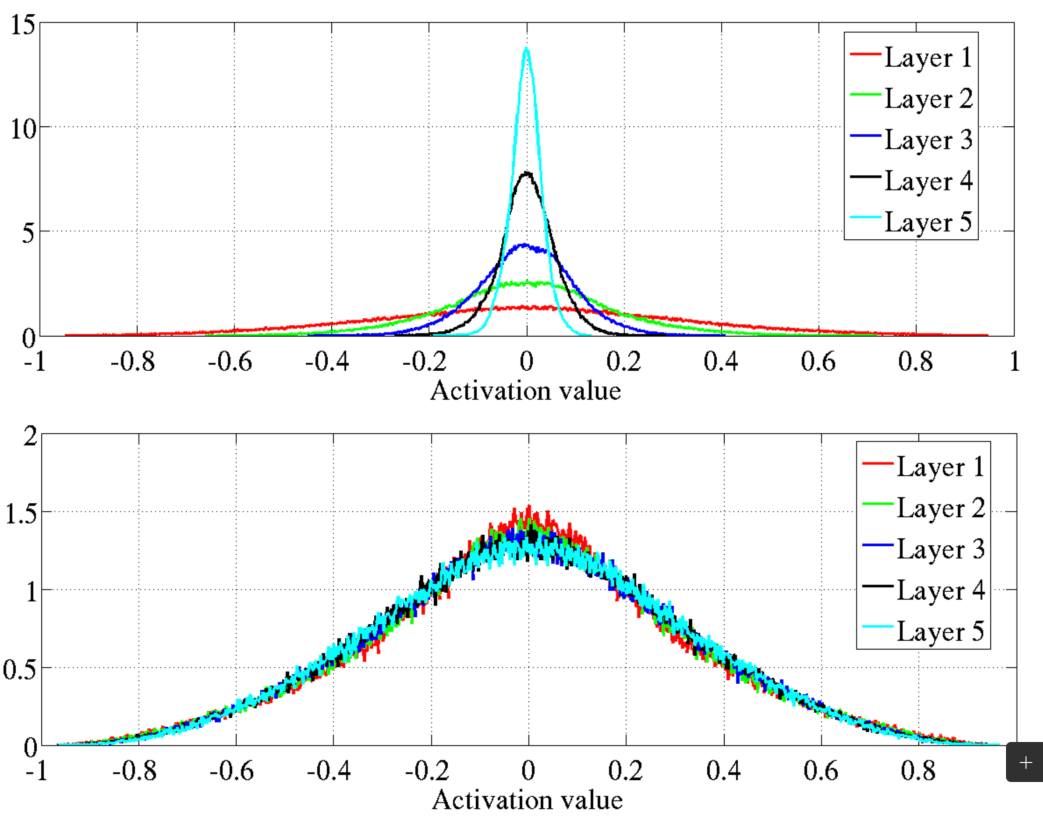
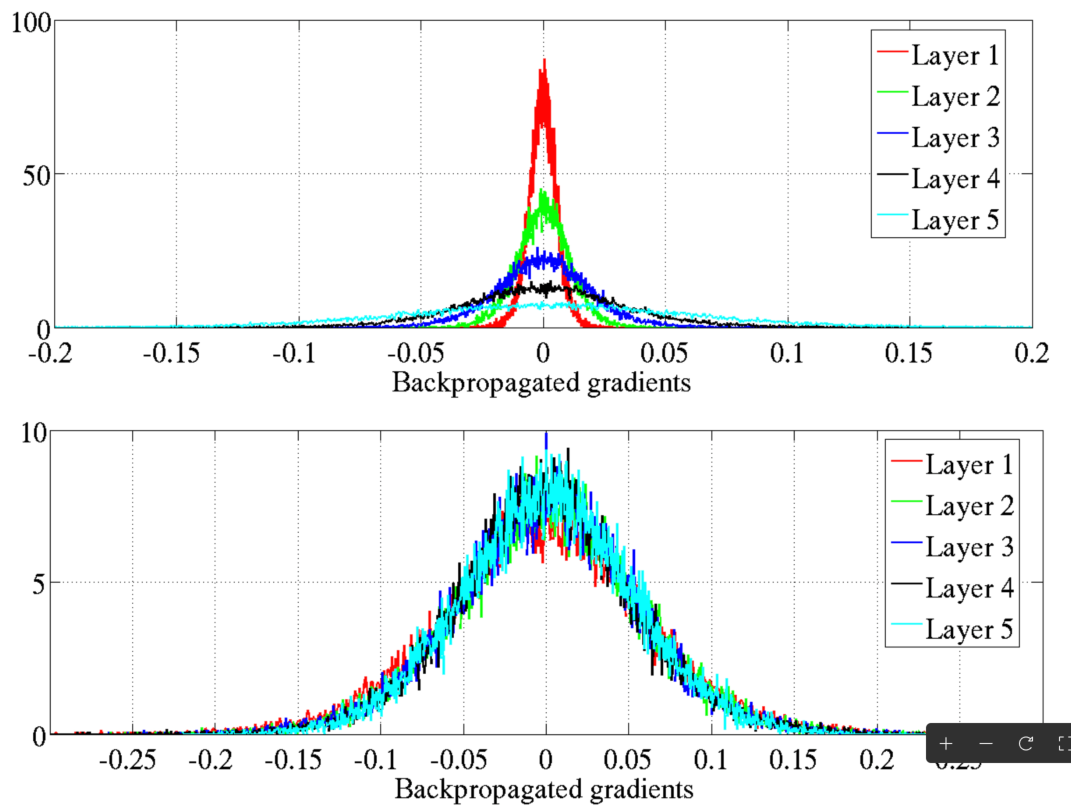
Vanishing gradients

• Vanishing gradient problem: Gradients become too small, hindering weight updates.

• Stalled neural network research (again) in early 2000s.

• Sigmoid and its derivative (range: 0 to 0.25) were key factors.

• Common initialization: Weights/biases from \(\mathcal{N}(0, 1)\) contributed to the issue.

Glorot and Bengio (2010) shed light on the problems.

The vanishing gradient problem often occurs with activation functions like the sigmoid and hyperbolic tangent (tanh), leading to difficulties in training deep neural networks due to diminishing gradients that slow down learning.

In contrast, the exploding gradient problem, which involves gradients growing excessively large, is typically observed in architectures such as recurrent neural networks (RNNs).

Both issues can significantly affect the stability and convergence of gradient-based optimization techniques, thereby hindering the effective training of deep models.

Vanishing gradients: solutions

• Alternative activation functions: Rectified Linear Unit (ReLU) and its variants (e.g., Leaky ReLU, Parametric ReLU, and Exponential Linear Unit).

• Weight Initialization: Xavier (Glorot) or He initialization.

Other techniques exists to mitigate the problem, including those:

• Batch Normalization: Implement batch normalization to standardize the inputs to each layer, which can help stabilize and accelerate training by reducing internal covariate shift and maintaining effective gradient flow.

• Residual Networks: Use residual connections, as seen in ResNet architectures, which allow gradients to flow more easily through the network by providing shortcut paths that bypass one or more layers.

Glorot and Bengio

Figure 6

Figure 7

The graphs presented illustrate the normalized histograms of activation values and back-propagated gradients associated with the hyperbolic tangent activation function.

The produce the top diagrams, Glorot and Bengio used an initialization method that was popular at the time, whereas the bottom diagrams have been produced using a new scheme (Glorot).

In Glorot & Bengio (2010), layers are numbered from input (layer 1) to output (layer L).

So:

• Early layers = close to input.
• Later layers = close to output.

Figures 6 and 7 present histograms depicting activation values and gradient values, respectively, for each layer.

• Activations:

  In networks suffering from the vanishing gradient problem, activations tend to shrink as we move from input to output — i.e. lower mean and variance in deeper layers. The deeper you go, the “flatter” the signal becomes.

• Gradients:

  Conversely, gradients vanish as we go from the output layer back toward the input. Small gradients in early (input-side) layers, somewhat larger near the output.

So:

• Low activations deeper in the network.
• Low gradients toward the input.

Glorot & Bengio’s main contributions and messages:

1. Root cause identified:

   They analyzed how the variance of activations and gradients evolves across layers, showing that improper initialization causes the signal (both forward and backward) to either vanish or explode exponentially with depth.

2. Analytical condition:

   For stable training, the variance of activations and gradients should remain roughly constant across layers.

   This led to the “Xavier initialization” (now standard):

\[ \text{Var}(W) = \frac{2}{n_\text{in} + n_\text{out}} \]

which keeps signal variance balanced both ways.

3. Empirical verification:

   Figures 6 and 7 demonstrate how poor initialization (e.g., too small or too large) causes vanishing/exploding activations and gradients, while Xavier initialization keeps them stable.

4. Broader message:

   Successful deep learning depends crucially on:

   • Proper weight initialization (maintaining signal flow).
   • Appropriate activation functions (e.g. sigmoid vs tanh vs ReLU).
   • Balanced scaling of activations and gradients during both forward and backward passes.

Vanishing gradient

• Mechanism:

  In deep networks with saturating nonlinearities (like sigmoid/tanh), backprop multiplies many small derivatives (<1), causing exponentially smaller gradients in earlier layers.

• Effect:

  Early layers learn extremely slowly, effectively “frozen” — while later layers (closer to output) keep adapting.

• Solutions:

  • Xavier or He initialization (variance-preserving).
  • Non-saturating activations (ReLU family).

Glorot and Bengio (2010), page 254.

He initialization

A similar but slightly different initialization method design to work with ReLU, as well as Leaky ReLU, ELU, GELU, Swish, and Mish.

Ensure that the initialization method matches the chosen activation function.

import tensorflow as tf
from tensorflow.python.keras.layers import Dense

dense = Dense(50, activation="relu", kernel_initializer="he_normal")

• Glorot Initialization (Xavier Initialization): This method sets the initial weights based on the number of input and output units for each layer, aiming to keep the variance of activations consistent across layers. It is particularly effective for activation functions like sigmoid and tanh.

• He Initialization: This approach adjusts the weight initialization to be suitable for layers using ReLU and its variants, by scaling the variance according to the number of input units only.

AKA Kaiming initialization.

Note

Randomly initializing the weights¹ is sufficient to break symmetry in a neural network, allowing the bias terms to be set to zero without impacting the network’s ability to learn effectively.

1. Proper initialization of weights, such as using Xavier/Glorot or He initialization, is crucial and should be aligned with the choice of activation function to ensure optimal network performance.

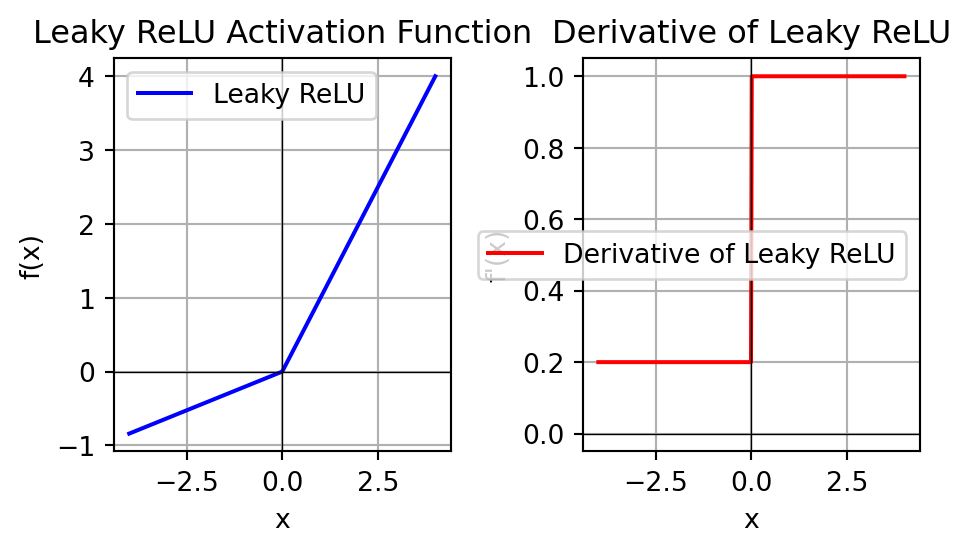
Activation Function: Leaky ReLU

import numpy as np
import matplotlib.pyplot as plt

# Define the Leaky ReLU function
def leaky_relu(x, alpha=0.21):
    return np.where(x > 0, x, alpha * x)

# Define the derivative of the Leaky ReLU function
def leaky_relu_derivative(x, alpha=0.2):
    return np.where(x > 0, 1, alpha)

# Generate a range of input values
x_values = np.linspace(-4, 4, 400)

# Compute the Leaky ReLU and its derivative
leaky_relu_values = leaky_relu(x_values)
leaky_relu_derivative_values = leaky_relu_derivative(x_values)

# Create the plot
plt.figure(figsize=(5, 3))

# Plot the Leaky ReLU
plt.subplot(1, 2, 1)
plt.plot(x_values, leaky_relu_values, label='Leaky ReLU', color='blue')
plt.title('Leaky ReLU Activation Function')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.grid(True)
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.legend()

# Plot the derivative of the Leaky ReLU
plt.subplot(1, 2, 2)
plt.plot(x_values, leaky_relu_derivative_values, label='Derivative of Leaky ReLU', color='red')
plt.title('Derivative of Leaky ReLU')
plt.xlabel('x')
plt.ylabel("f'(x)")
plt.grid(True)
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.legend()

# Show the plots
plt.tight_layout()
plt.show()

When the input to the ReLU activation function, the weighted sum plus bias, is negative for all the training examples, the output value of ReLU is zero. But also, its derivative is 0, which effectively deactivates the neuron. Leaky ReLU, or other variants, effectively mitigates the issue.

import tensorflow as tf
from tensorflow.python.keras.layers import Dense

leaky_relu = tf.keras.layers.LeakyReLU(negative_slope=0.2)
dense = tf.keras.layers.Dense(50, activation=leaky_relu, kernel_initializer="he_normal")

Keras proposes 18 layer activation functions at the time of writing.

The Leaky ReLU, a variant of the standard ReLU activation function, effectively mitigates the issue of dying ReLU nodes. For negative input values, it introduces a linear component with a slope governed by the parameter negative_slope.

Output layer

Output Layer: Regression Task

• # of output neurons:
  • 1 per dimension
• Output layer activation function:
  • None, ReLU/softplus, if positive, sigmoid/tanh, if bounded
• Loss function:
  • MeanSquaredError

In an object detection problem, determining the bounding box exemplifies a regression task where the output is multidimensional.

Output Layer: Classification Task

• # of output neurons:
  • 1 if binary, 1 per class, if multi-label or multiclass.
• Output layer activation function:
  • sigmoid, if binary or multi-label, softmax if multi-class.
• Loss function:
  • cross-entropy

Softmax

Observe that I have revised the representation of the output nodes to indicate that the softmax function is applied to the entire layer, rather than to individual nodes. This function transforms the raw output values of the layer into probabilities that sum to 1, facilitating multi-class classification. This characteristic distinguishes it from activation functions like ReLU or sigmoid, which are typically applied independently to each node’s output.

The \(\argmax\) function is not suitable for optimization via gradient-based methods because its derivative is zero in all cases, similar to step functions. In contrast, the softmax function offers both a probabilistic interpretation and a computable derivative, making it more effective for such applications.

The \(\argmax\) function can be applied a posteriori to trained networks for class prediction.

Softmax ensures that all activation outputs fall between 0 and 1 and collectively sum to 1.

Softmax

The softmax function is an activation function used in multi-class classification problems to convert a vector of raw scores into probabilities that sum to 1.

Given a vector \(\mathbf{z} = [z_1, z_2, \ldots, z_n]\):

\[ \sigma(\mathbf{z})_i = \frac{e^{z_i}}{\sum_{j=1}^{n} e^{z_j}} \]

where \(\sigma(\mathbf{z})_i\) is the probability of the \(i\)-th class, and \(n\) is the number of classes.

Softmax emphasizes higher scores while suppressing lower ones, enabling a probabilistic interpretation of the outputs.

We clearly see that such an activation applies for an entire layer since the denomination depends on the values of all the \(z_j\), for \(j in 1 \ldots n\).

Softmax

\(z_1\)	\(z_2\)	\(z_3\)	\(\sigma(z_1)\)	\(\sigma(z_2)\)	\(\sigma(z_3)\)	\(\sum\)
1.47	-0.39	0.22	0.69	0.11	0.20	1.00
5.00	6.00	4.00	0.24	0.67	0.09	1.00
0.90	0.80	1.10	0.32	0.29	0.39	1.00
-2.00	2.00	-3.00	0.02	0.98	0.01	1.00

1. Maintains Relative Order: The softmax function preserves the relative order of the input values. If one input is greater than another, its corresponding output will also be greater.

2. Interpreted as probabilities: Each value is in the range 0 to 1. The output values from the softmax function are normalized to sum to one, which allows them to be interpreted as probabilities.

3. Relative Differences: When the relative differences among the input values are small, the differences in the output probabilities remain small, reflecting the input distribution. When the input values are identical, the output values will be \(\frac{1}{n}\), where \(n\) is the number of classes.

4. Wide Range of Values: The softmax function can effectively handle a wide range of input values, thanks to the exponential function and normalization, which scale the inputs to a probabilistic range.

These properties make the softmax function particularly useful for multi-class classification tasks in machine learning.

Softmax values for a vector of length 3.

Softmax

Cross-entropy loss function

The cross-entropy in a multi-class classification task for one example:

\[ J(W) = -\sum_{k=1}^{K} y_k \log(\hat{y}_k) \]

Where:

• \(K\) is the number of classes.
• \(y_k\) is the true distribution for the class \(k\).
• \(\hat{y}_k\) is the predicted probability of class \(k\) from the model.

• The target vector \(y\) is expressed as a one-hot encoded vector of length \(K\), where the element corresponding to the true class is set to 1, and all other elements are 0.

• Consequently, in the summation over classes, only the term associated with the true class contributes a non-zero value.

• Therefore, the cross-entropy loss for a single example is given by \(-\log(\hat{y}_k)\), where \(\hat{y}_k\) is the predicted probability for the true class.

• The predicted probability \(\hat{y}_k\) is derived from the softmax function applied in the output layer of the neural network.

Cross-entropy loss function

• Classification Problem: 3 classes
  • Versicolour, Setosa, Virginica.
• One-Hot Encoding:
  • Setosa = \([0, 1, 0]\).
• Softmax Outputs & Loss:
  • \([0.22,\mathbf{0.7}, 0.08]\): Loss = \(-\log(0.7) = 0.3567\).
  • \([0.7, \mathbf{0.22}, 0.08]\): Loss = \(-\log(0.22) = 1.5141\).
  • \([0.7, \mathbf{0.08}, 0.22]\): Loss = \(-\log(0.08) = 2.5257\).

Among the softmax outputs, cross-entropy evaluates only the component corresponding to \(k=1\) (Setosa), as the other entries in the one-hot encoded vector are zero. This relevant element is highlighted in bold. When the softmax prediction aligns closely with the expected value, the resulting loss is minimal (0.3567). Conversely, as the prediction deviates further from the expected value, the loss increases (1.5141 and 2.5257).

Case: one example

• In the summation, only the term where \(y_k = 1\) contributes a non-zero value.

• Due to the negative sign preceding the summation, the value of the function is \(-\log(\hat{y}_k\).

• If the predicted probability \(\hat{y}_k\) is near 1, the loss approaches zero, indicating minimal penalty.

• Conversely, as \(\hat{y}_k\) nears 0, indicating an incorrect prediction, the loss approaches infinity. This substantial penalty allows cross-entropy loss to converge more quickly than mean squared error.

Case: dataset

For a dataset with \(N\) examples, the average cross-entropy loss over all examples is computed as:

\[ L = -\frac{1}{N} \sum_{i=1}^{N} \sum_{k=1}^{K} y_{i,k} \log(\hat{y}_{i,k}) \]

Where:

• \(i\) indexes over the different examples in the dataset.
• \(y_{i,k}\) and \(\hat{y}_{i,k}\) are the true and predicted probabilities for class \(k\) of example \(i\), respectively.

Regularization

Definition

Regularization comprises a set of techniques designed to enhance a model’s ability to generalize by mitigating overfitting. By discouraging excessive model complexity, these methods improve the model’s robustness and performance on unseen data.

Adding penalty terms to the loss

• In numerical optimization, it is standard practice to incorporate additional terms into the objective function to deter undesirable model characteristics.

• For a minimization problem, the optimization process aims to circumvent the substantial costs associated with these penalty terms.

Loss function

Consider the mean absolute error loss function:

\[ \mathrm{MAE}(X,W) = \frac{1}{N} \sum_{i=1}^N | h_W(x_i) - y_i | \]

Where:

• \(W\) are the weights of our network.
• \(h_W(x_i)\) is the output of the network for example \(i\).
• \(y_i\) is the true label for example \(i\).

Penalty term(s)

One or more terms can be added to the loss:

\[ \mathrm{MAE}(X,W) = \frac{1}{N} \sum_{i=1}^N | h_W(x_i) - y_i | + \mathrm{penalty} \]

Norm

A norm is assigns a non-negative length to a vector.

The \(\ell_p\) norm of a vector \(\mathbf{z} = [z_1, z_2, \ldots, z_n]\) is defined as:

\[ \|\mathbf{z}\|_p = \left( \sum_{i=1}^{n} |z_i|^p \right)^{1/p} \]

A norm is a function that assigns a non-negative length or size to each vector in a vector space, satisfying certain properties: positivity, scalar multiplication, the triangle inequality, and the property that the norm is zero if and only if the vector is zero.

With larger \(p\), the \(\ell_p\) norm increasingly highlights larger \(z_i\) values due to exponentiation.

\(\ell_1\) and \(\ell_2\) norms

The \(\ell_1\) norm (Manhattan norm) is:

\[ \|\mathbf{z}\|_1 = \sum_{i=1}^{n} |z_i| \]

The \(\ell_2\) norm (Euclidean norm) is:

\[ \|\mathbf{z}\|_2 = \sqrt{\sum_{i=1}^{n} z_i^2} \]

\(\ell_1\) and \(\ell_2\) regularization

Below, \(\alpha\) and \(\beta\) determine the degree of regularization applied; setting these values to zero effectively disables the regularization term. \[ \mathrm{MAE}(X,W) = \frac{1}{N} \sum_{i=1}^N | h_W(x_i) - y_i | + \alpha \ell_1 + \beta \ell_2 \]

Guidelines

• \(\ell_1\) Regularization:
  • Promotes sparsity, setting many weights to zero.
  • Useful for feature selection by reducing feature reliance.
• \(\ell_2\) Regularization:
  • Promotes small, distributed weights for stability.
  • Ideal when all features contribute and reducing complexity is key.

Keras example

import tensorflow as tf
from tensorflow.python.keras.layers import Dense

regularizer = tf.keras.regularizers.l2(0.001)

dense = Dense(50, kernel_regularizer=regularizer)

This layer specifically utilizes \(\ell_2\) regularization, in contrast to the prior discussion where regularization was applied globally across the entire model.

Dropout

Dropout is a regularization technique in neural networks where randomly selected neurons are ignored during training, reducing overfitting by preventing co-adaptation of features.

Hinton et al. (2012)

Dropout

• During each training step, each neuron in a dropout layer has a probability \(p\) of being excluded from the computation, typical values for \(p\) are between 10% and 50%.

• While seemingly counterintuitive, this approach prevents the network from depending on specific neurons, promoting the distribution of learned representations across multiple neurons.

Dropout

• Dropout is one of the most popular and effective methods for reducing overfitting.

• The typical improvement in performance is modest, usually around 1 to 2%.

Keras

import keras
from keras.models import Sequential
from keras.layers import InputLayer, Dropout, Flatten, Dense

model = tf.keras.Sequential([
    InputLayer(shape=[28, 28]),
    Flatten(),
    Dropout(rate=0.2),
    Dense(300, activation="relu"),
    Dropout(rate=0.2),
    Dense(100, activation="relu"),
    Dropout(rate=0.2),
    Dense(10, activation="softmax")
])

The dropout rate may differ between layers; larger rates can be applied to larger layers, while smaller rates are suitable for smaller layers. It is common practice in many networks to apply dropout only after the final hidden layer.

Adding Dropout layers to the Fashion-MNIST model from last lecture.

Definition

Early stopping is a regularization technique that halts training once the model’s performance on a validation set begins to degrade, preventing overfitting by stopping before the model learns noise.

Geoffrey Hinton calls this the “beautiful free lunch.”

Early Stopping

Attribution: Géron (2022), 04_training_linear_models.ipynb.

Prologue

Summary

Attribution: Angermueller et al. (2016)

Summary

Concept	Role
Activation functions	Introduce non-linearity (e.g., Sigmoid, ReLU).
Loss function	Measures prediction error (e.g., Binary Cross-Entropy).
Learning rate (α)	Controls step size in parameter updates.
Gradient descent	Optimization method for weight adjustment.
Chain rule	Mechanism for propagating derivatives backward.
Automatic differentiation	Software implementation of backprop (e.g., TensorFlow, PyTorch).

Summary

• Vanishing Gradient Problem:
  • Gradients become too small during backpropagation, hindering training.
  • Mitigation strategies include using ReLU activation functions and proper weight initialization (Glorot or He initialization).
• Weight Initialization:
  • Random initialization breaks symmetry and allows effective learning.
  • Glorot initialization suits sigmoid and tanh activations.
  • He initialization is optimal for ReLU and its variants.
• Loss Functions:
  • Regression Tasks: Mean Squared Error (MSE).
  • Classification Tasks: Cross-Entropy Loss with Softmax activation for multi-class outputs.
• Regularization Techniques:
  • L1 and L2 Regularization: Add penalty terms to the loss to discourage large weights.
  • Dropout: Randomly deactivate neurons during training to prevent overfitting.
  • Early Stopping: Halt training when validation performance deteriorates.

3Blue1Brown

A series of videos, with animations, providing the intuition behind the backpropagation algorithm.

• Neural networks (playlist)

  • What is backpropagation really doing? (12m 47s)
  • Backpropagation calculus (10m 18s)

Prerequisite: Gradient descent, how neural networks learn? (20m 33s)

StatQuest

• Neural Networks Pt. 2: Backpropagation Main Ideas (17m 34s)
• Backpropagation Details Pt. 1: Optimizing 3 parameters simultaneously (18m 32s)
• Backpropagation Details Pt. 2: Going bonkers with The Chain Rule (13m 9s)

Prerequisites: The Chain Rule (18m 24s) & Gradient Descent, Step-by-Step (23m 54s)

Herman Kamper

One of the most thorough series of videos on the backpropagation algorithm.

• Introduction to neural networks (playlist)

  • Backpropagation (without forks) (31m 1s)
  • Backprop for a multilayer feedforward neural network (4m 2s)
  • Computational graphs and automatic differentiation for neural networks (6m 56s)
  • Common derivatives for neural networks (7m 18s)
  • A general notation for derivatives (in neural networks) (7m 56s)
  • Forks in neural networks (13m 46s)
  • Backpropagation in general (now with forks) (3m 42s)

Free book with implementation

In his book, Neural Networks and Deep Learning, Michael Nielsen provides a comprehensive Python implementation of a neural network.

Next lecture

• We will introduce various architectures of artificial neural networks.

References

Angermueller, Christof, Tanel Pärnamaa, Leopold Parts, and Oliver Stegle. 2016. “Deep Learning for Computational Biology.” Mol Syst Biol 12 (7): 878. https://doi.org/10.15252/msb.20156651.

Baydin, Atılım Günes, Barak A. Pearlmutter, Alexey Andreyevich Radul, and Jeffrey Mark Siskind. 2017. “Automatic Differentiation in Machine Learning: A Survey.” J. Mach. Learn. Res. 18 (1): 5595–5637.

Géron, Aurélien. 2022. Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow. 3rd ed. O’Reilly Media, Inc.

Glorot, Xavier, and Yoshua Bengio. 2010. “Understanding the Difficulty of Training Deep Feedforward Neural Networks.” In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, edited by Yee Whye Teh and Mike Titterington, 9:249–56. Proceedings of Machine Learning Research. Chia Laguna Resort, Sardinia, Italy: PMLR. https://proceedings.mlr.press/v9/glorot10a.html.

Hinton, Geoffrey E., Nitish Srivastava, Alex Krizhevsky, Ilya Sutskever, and Ruslan Salakhutdinov. 2012. “Improving Neural Networks by Preventing Co-Adaptation of Feature Detectors.” CoRR abs/1207.0580. http://arxiv.org/abs/1207.0580.

Rumelhart, David E., Geoffrey E. Hinton, and Ronald J. Williams. 1986. “Learning representations by back-propagating errors.” Nature 323 (6088): 533–36. https://doi.org/10.1038/323533a0.

Russell, Stuart, and Peter Norvig. 2020. Artificial Intelligence: A Modern Approach. 4th ed. Pearson. http://aima.cs.berkeley.edu/.

Marcel Turcotte

Marcel.Turcotte@uOttawa.ca

School of Electrical Engineering and Computer Science (EECS)

University of Ottawa