Softmax, cross-entropy, regularization

CSI 4106 - Fall 2026

Marcel Turcotte

Version: Aug 10, 2026 11:53

Preamble

Message of the Day

Why 2025 is the single most pivotal year in our lifetime, Peter Leyden, Big Think, YouTube, 2025-10-20.

Learning objectives

• Explain the role of softmax and cross-entropy loss in measuring the dissimilarity between predicted and true probability distributions.
• Explore methods like L1, L2 regularization, and dropout to enhance neural networks’ generalization capabilities.

In the previous lecture, we examined the backpropagation algorithm, which provides a systematic method for calculating the partial derivatives of the loss function. This calculation is essential for applying the gradient descent algorithm, thus enabling the adjustment of weights in a deep neural network. Today, we will look at what happens at the output layer and regularization techniques.

Output Layers

Output Layer: Regression Task

• # of output neurons:
  • 1 per dimension
• Output layer activation function:
  • None, ReLU/softplus, if positive, sigmoid/tanh, if bounded
• Loss function:
  • MeanSquaredError

How does one select an appropriate activation function?

In a feed-forward network, activation functions in the hidden layers are chosen mainly for their impact on performance and convergence, while the activation function in the output layer is selected according to the requirements of the task.

• Hidden layers:

  The activation function (e.g., ReLU, GELU, tanh) mainly affects training dynamics — such as gradient flow, nonlinearity strength, and convergence rate. The choice is typically empirical, guided by performance, numerical stability, and optimization behavior.

• Output layer:

  The activation function is determined by the nature of the prediction task:

  • Regression: linear, ReLU, or softplus (depending on range constraints)
  • Binary classification: sigmoid
  • Multi-class classification: softmax
  • Multi-label classification: sigmoid (per output unit)

Examples of multi-output regression problems (2–4 outputs) include:

• 2 outputs:

  • Predicting both the latitude and longitude of a location from an image.
  • Estimating the width and height of a bounding box in object detection.
  • Forecasting temperature and humidity simultaneously.

• 3 outputs:

  • Predicting the x, y, z coordinates of a point in space (e.g., hand-joint localization).
  • Estimating RGB color values from spectral measurements.

• 4 outputs:

  • Predicting bounding box coordinates — (x_{min}, y_{min}, x_{max}, y_{max}) — in object detection.

In an object detection problem, determining the bounding box exemplifies a regression task where the output is multidimensional.

Output Layer: Multi-Label

However, this network is not suitable for classification. Do you see why?

With the sigmoid activation function, this network makes multi-label predictions.

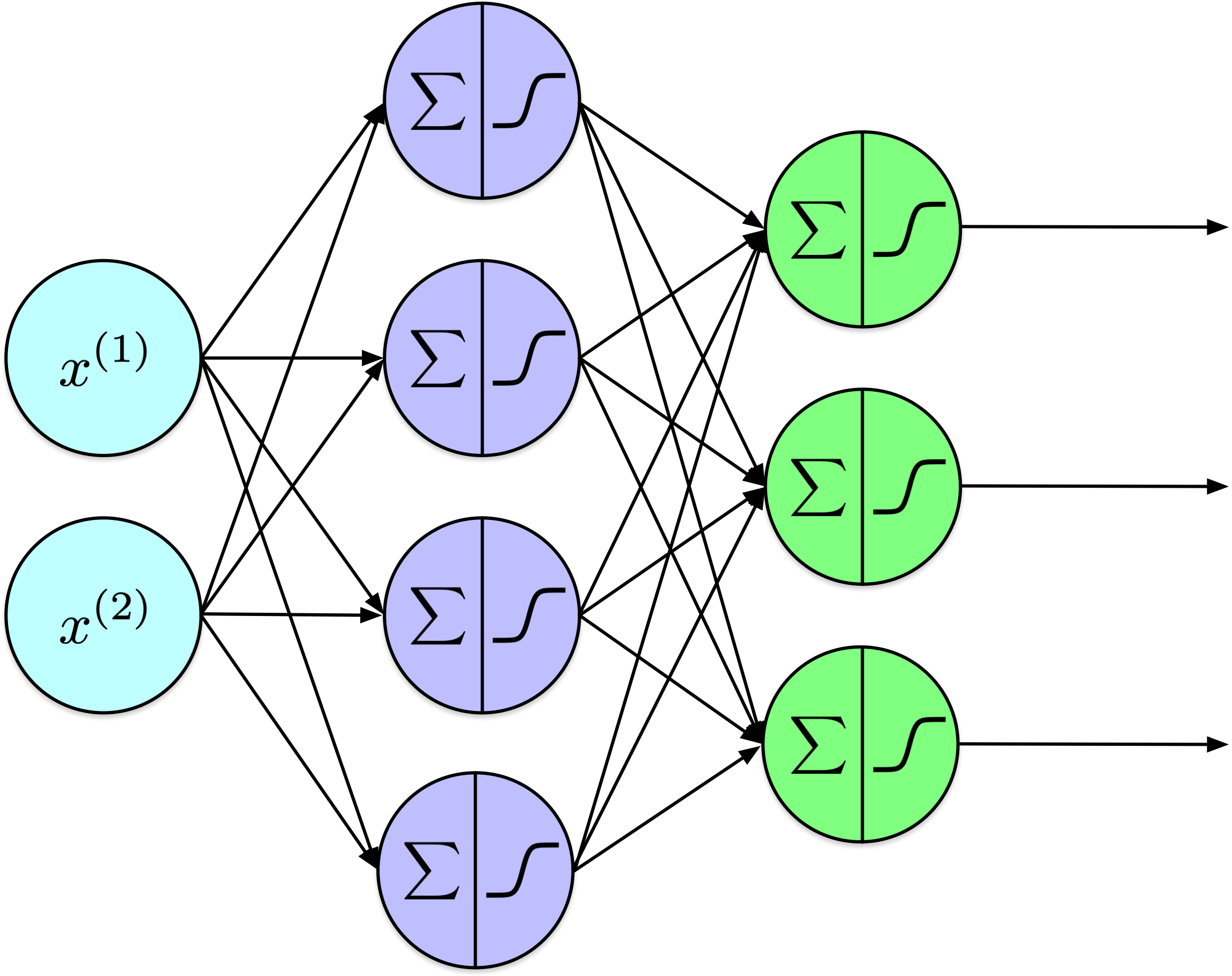
Output Layer: Classification Task

• # of output neurons:
  • 1 if binary, 1 per class, if multi-label or multiclass.
• Output layer activation function:
  • sigmoid, if binary or multi-label, softmax if multi-class.
• Loss function:
  • cross-entropy

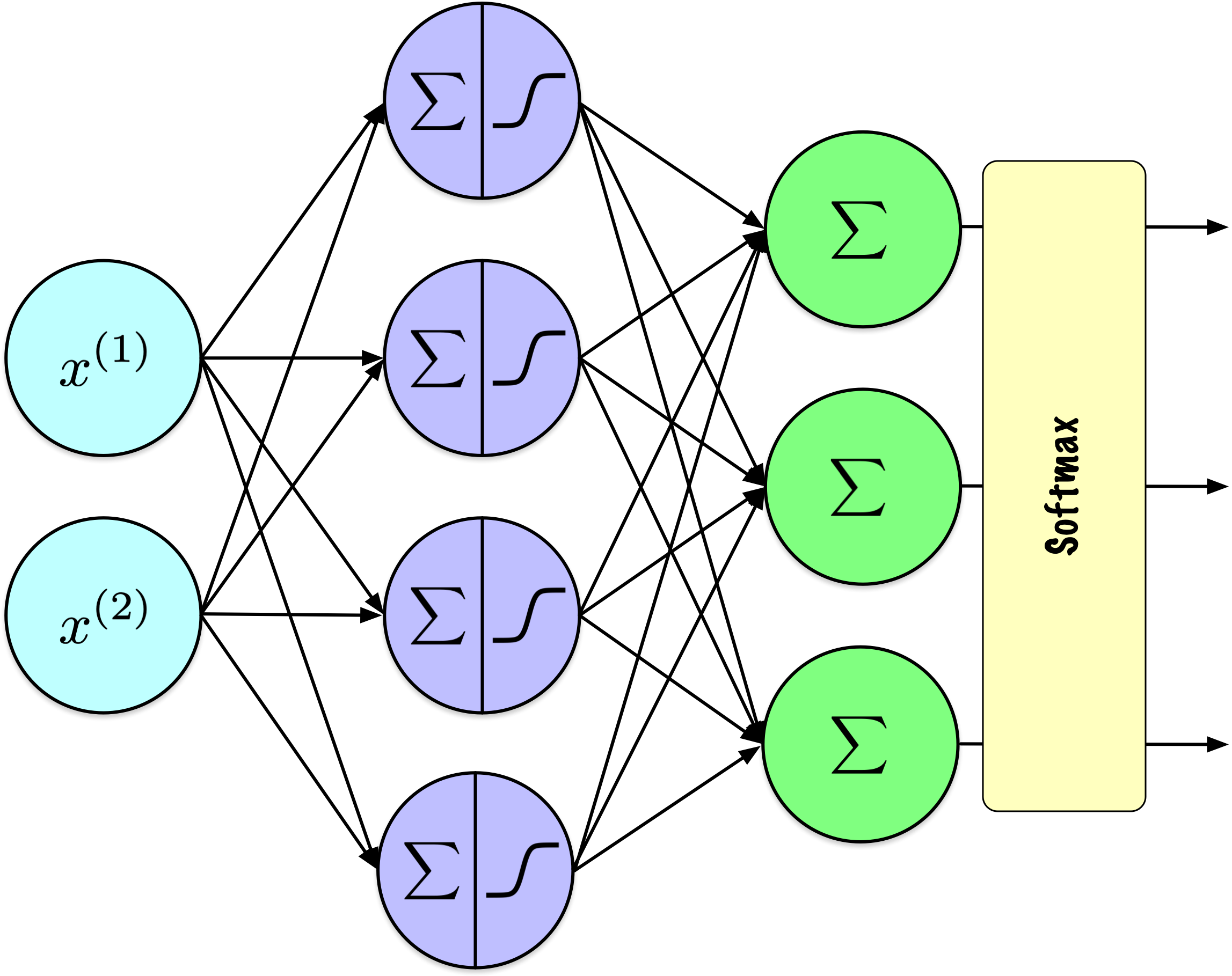
Softmax

Observe that I have revised the representation of the output nodes to indicate that the softmax function is applied to the entire layer, rather than to individual nodes. This function transforms the raw output values of the layer into probabilities that sum to 1, facilitating multi-class classification. This characteristic distinguishes it from activation functions like ReLU or sigmoid, which are typically applied independently to each node’s output.

The \argmax function is not suitable for optimization via gradient-based methods because its derivative is zero in all cases, similar to step functions. In contrast, the softmax function offers both a probabilistic interpretation and a computable derivative, making it more effective for such applications.

The \argmax function can be applied a posteriori to trained networks for class prediction.

Softmax ensures that all activation outputs fall between 0 and 1 and collectively sum to 1.

Softmax

The softmax function is an activation function used in multi-class classification problems to convert a vector of raw scores into probabilities that sum to 1.

Given a vector \mathbf{z} = [z_1, z_2, \ldots, z_n]:

\sigma(\mathbf{z})_i = \frac{e^{z_i}}{\sum_{j=1}^{n} e^{z_j}}

where \sigma(\mathbf{z})_i is the probability of the i-th class, and n is the number of classes.

Softmax emphasizes higher scores while suppressing lower ones, enabling a probabilistic interpretation of the outputs.

We clearly see that such an activation applies for an entire layer since the denomination depends on the values of all the z_j, for j in 1 \ldots n.

In the softmax function, exponentiation serves a crucial mathematical and conceptual role: it transforms arbitrary real-valued scores into positive, normalized probabilities while amplifying differences between inputs.

1. Ensures positivity:

   The exponential function guarantees all outputs are positive, a necessary property for valid probabilities.

2. Magnifies relative differences:

   Exponentiation is a monotonic nonlinear transformation that increases large values much more than small ones. If one logit is slightly larger, e^{z_i} becomes disproportionately larger, sharpening the distribution (useful for emphasizing the most likely class).

3. Preserves ordering:

   Since e^x is strictly increasing, the class with the highest logit before softmax remains the one with the highest probability after.

4. Facilitates gradient-based learning:

   The exponential smooths the transition between classes, providing differentiable outputs and stable gradients for optimization with cross-entropy.

A logit is a pre-activation value (z_i). Each neuron in the output layer (before activation) produces a logit z_i.

Softmax

z_1	z_2	z_3	\sigma(z_1)	\sigma(z_2)	\sigma(z_3)	\sum
1.47	-0.39	0.22	0.69	0.11	0.20	1.00
5.00	6.00	4.00	0.24	0.67	0.09	1.00
0.90	0.80	1.10	0.32	0.29	0.39	1.00
-2.00	2.00	-3.00	0.02	0.98	0.01	1.00

1. Maintains Relative Order: The softmax function preserves the relative order of the input values. If one input is greater than another, its corresponding output will also be greater.

2. Interpreted as probabilities: Each value is in the range 0 to 1. The output values from the softmax function are normalized to sum to one, which allows them to be interpreted as probabilities.

3. Relative Differences: When the relative differences among the input values are small, the differences in the output probabilities remain small, reflecting the input distribution. When the input values are identical, the output values will be \frac{1}{n}, where n is the number of classes.

4. Wide Range of Values: The softmax function can effectively handle a wide range of input values, thanks to the exponential function and normalization, which scale the inputs to a probabilistic range.

These properties make the softmax function particularly useful for multi-class classification tasks in machine learning.

Softmax values for a vector of length 3.

Softmax

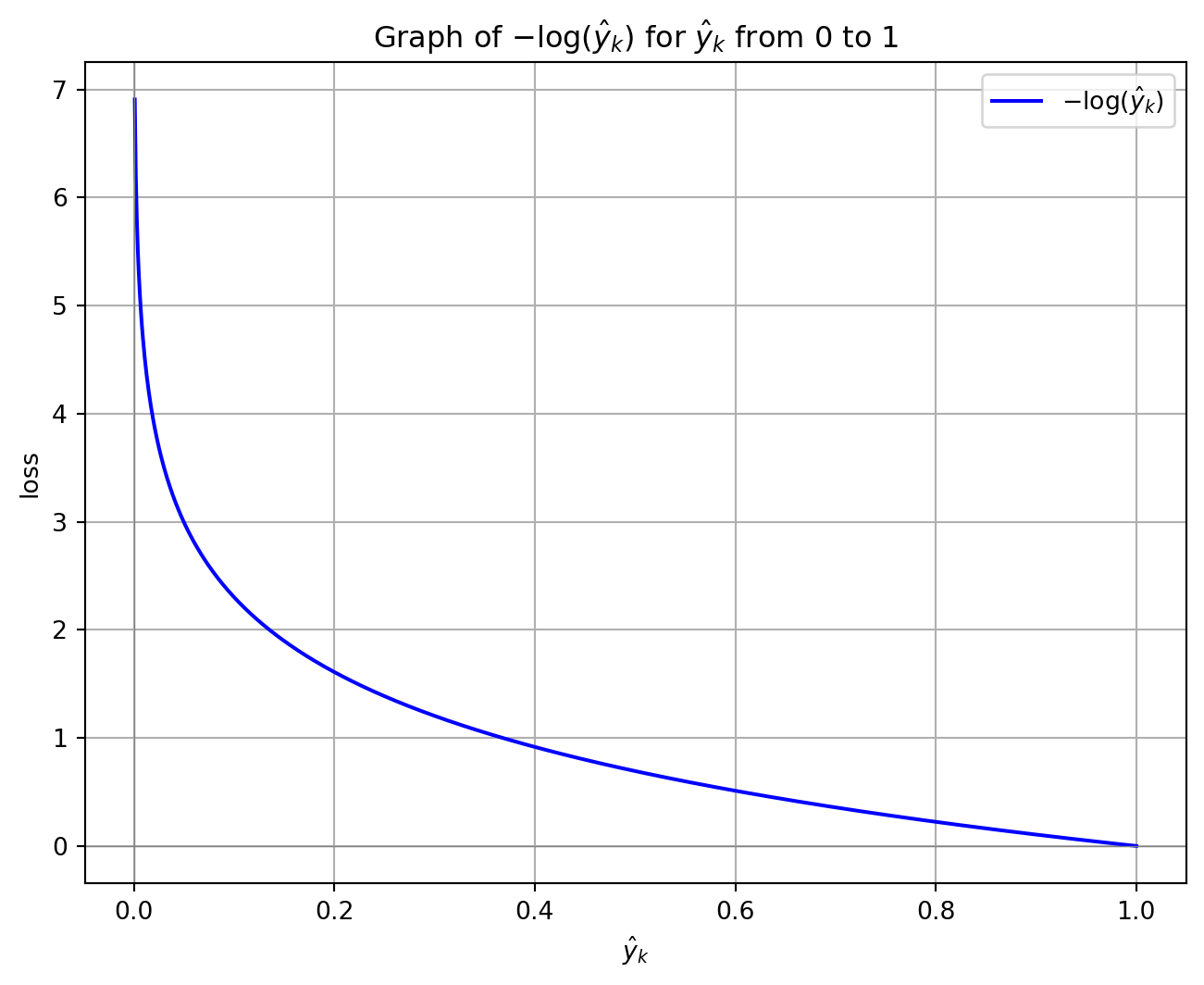
Cross-entropy loss function

The cross-entropy in a multi-class classification task for one example:

J(W) = -\sum_{k=1}^{K} y_k \log(\hat{y}_k)

Where:

• K is the number of classes.
• y_k is the true distribution for the class k.
• \hat{y}_k is the predicted probability of class k from the model.

• The target vector y is expressed as a one-hot encoded vector of length K, where the element corresponding to the true class is set to 1, and all other elements are 0.

• Consequently, in the summation over classes, only the term associated with the true class contributes a non-zero value.

• Therefore, the cross-entropy loss for a single example is given by -\log(\hat{y}_k), where \hat{y}_k is the predicted probability for the true class.

• The predicted probability \hat{y}_k is derived from the softmax function applied in the output layer of the neural network.

Cross-entropy loss function

• Classification Problem: 3 classes
  • Versicolour, Setosa, Virginica.
• One-Hot Encoding:
  • Setosa = [0, 1, 0].
• Softmax Outputs & Loss:
  • [0.22,\mathbf{0.7}, 0.08]: Loss = -\log(0.7) = 0.3567.
  • [0.7, \mathbf{0.22}, 0.08]: Loss = -\log(0.22) = 1.5141.
  • [0.7, \mathbf{0.08}, 0.22]: Loss = -\log(0.08) = 2.5257.

Among the softmax outputs, cross-entropy evaluates only the component corresponding to k=1 (Setosa), as the other entries in the one-hot encoded vector are zero. This relevant element is highlighted in bold. When the softmax prediction aligns closely with the expected value, the resulting loss is minimal (0.3567). Conversely, as the prediction deviates further from the expected value, the loss increases (1.5141 and 2.5257).

Case: one example

• In the summation, only the term where y_k = 1 contributes a non-zero value.

• Due to the negative sign preceding the summation, the value of the function is -\log(\hat{y}_k.

• If the predicted probability \hat{y}_k is near 1, the loss approaches zero, indicating minimal penalty.

• Conversely, as \hat{y}_k nears 0, indicating an incorrect prediction, the loss approaches infinity. This substantial penalty allows cross-entropy loss to converge more quickly than mean squared error.

Case: dataset

For a dataset with N examples, the average cross-entropy loss over all examples is computed as:

L = -\frac{1}{N} \sum_{i=1}^{N} \sum_{k=1}^{K} y_{i,k} \log(\hat{y}_{i,k})

Where:

• i indexes over the different examples in the dataset.
• y_{i,k} and \hat{y}_{i,k} are the true and predicted probabilities for class k of example i, respectively.

Regularization

Definition

Regularization comprises a set of techniques designed to enhance a model’s ability to generalize by mitigating overfitting. By discouraging excessive model complexity, these methods improve the model’s robustness and performance on unseen data.

Adding penalty terms to the loss

• In numerical optimization, it is standard practice to incorporate additional terms into the objective function to deter undesirable model characteristics.

• For a minimization problem, the optimization process aims to circumvent the substantial costs associated with these penalty terms.

Loss function

Consider the mean absolute error loss function:

\mathrm{MAE}(X,W) = \frac{1}{N} \sum_{i=1}^N | h_W(x_i) - y_i |

Where:

• W are the weights of our network.
• h_W(x_i) is the output of the network for example i.
• y_i is the true label for example i.

Penalty term(s)

One or more terms can be added to the loss:

\mathrm{MAE}(X,W) = \frac{1}{N} \sum_{i=1}^N | h_W(x_i) - y_i | + \mathrm{penalty}

Norm

A norm is assigns a non-negative length to a vector.

The \ell_p norm of a vector \mathbf{z} = [z_1, z_2, \ldots, z_n] is defined as:

\|\mathbf{z}\|_p = \left( \sum_{i=1}^{n} |z_i|^p \right)^{1/p}

A norm is a function that assigns a non-negative length or size to each vector in a vector space, satisfying certain properties: positivity, scalar multiplication, the triangle inequality, and the property that the norm is zero if and only if the vector is zero.

With larger p, the \ell_p norm increasingly highlights larger z_i values due to exponentiation.

\ell_1 and \ell_2 norms

The \ell_1 norm (Manhattan norm) is:

\|\mathbf{z}\|_1 = \sum_{i=1}^{n} |z_i|

The \ell_2 norm (Euclidean norm) is:

\|\mathbf{z}\|_2 = \sqrt{\sum_{i=1}^{n} z_i^2}

\ell_1 and \ell_2 regularization

Below, \alpha and \beta determine the degree of regularization applied; setting these values to zero effectively disables the regularization term. \mathrm{MAE}(X,W) = \frac{1}{N} \sum_{i=1}^N | h_W(x_i) - y_i | + \alpha \ell_1 + \beta \ell_2

Guidelines

• \ell_1 Regularization:
  • Promotes sparsity, setting many weights to zero.
  • Useful for feature selection by reducing feature reliance.
• \ell_2 Regularization:
  • Promotes small, distributed weights for stability.
  • Ideal when all features contribute and reducing complexity is key.

See kong_and_yu-2018 for an example.

Keras example

import tensorflow as tf
from tensorflow.python.keras.layers import Dense

regularizer = tf.keras.regularizers.l2(0.001)

dense = Dense(50, kernel_regularizer=regularizer)

This layer specifically utilizes \ell_2 regularization, in contrast to the prior discussion where regularization was applied globally across the entire model.

Dropout

Dropout is a regularization technique in neural networks where randomly selected neurons are ignored during training, reducing overfitting by preventing co-adaptation of features.

Hinton et al. (2012)

Dropout

• During each training step, each neuron in a dropout layer has a probability p of being excluded from the computation, typical values for p are between 10% and 50%.

• While seemingly counterintuitive, this approach prevents the network from depending on specific neurons, promoting the distribution of learned representations across multiple neurons.

Dropout

• Dropout is one of the most popular and effective methods for reducing overfitting.

• The typical improvement in performance is modest, usually around 1 to 2%.

During training, each neuron in a dropout layer is randomly excluded (set to zero) with a probability p—the dropout rate.

When dropout “sets a neuron to zero,” it means that for the current training step (mini-batch), that neuron’s output activation is replaced by zero. The neuron still exists in the network — its weights are not removed or altered — but its output contributes nothing to the forward or backward pass for that batch.

In the next batch, a new random mask is sampled, so a different subset of neurons is dropped. Over many iterations, all neurons participate, but never all at once.

At inference time, dropout is disabled—all neurons are active, and their outputs are not scaled.

Keras

import keras
from keras.models import Sequential
from keras.layers import InputLayer, Dropout, Flatten, Dense

model = tf.keras.Sequential([
    InputLayer(shape=[28, 28]),
    Flatten(),
    Dropout(rate=0.2),
    Dense(300, activation="relu"),
    Dropout(rate=0.2),
    Dense(100, activation="relu"),
    Dropout(rate=0.2),
    Dense(10, activation="softmax")
])

The dropout rate may differ between layers; larger rates can be applied to larger layers, while smaller rates are suitable for smaller layers. It is common practice in many networks to apply dropout only after the final hidden layer.

Adding Dropout layers to the Fashion-MNIST model from last lecture.

Definition

Early stopping is a regularization technique that halts training once the model’s performance on a validation set begins to degrade, preventing overfitting by stopping before the model learns noise.

Geoffrey Hinton calls this the “beautiful free lunch.”

Early Stopping

Attribution: Géron (2022), 04_training_linear_models.ipynb.

Prologue

Summary

• Loss Functions:
  • Regression Tasks: Mean Squared Error (MSE).
  • Classification Tasks: Cross-Entropy Loss with Softmax activation for multi-class outputs.
• Regularization Techniques:
  • L1 and L2 Regularization: Add penalty terms to the loss to discourage large weights.
  • Dropout: Randomly deactivate neurons during training to prevent overfitting.
  • Early Stopping: Halt training when validation performance deteriorates.

Next lecture

• We will introduce convolutional neural networks.

References

Géron, Aurélien. 2022. Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow. 3rd ed. O’Reilly Media, Inc.

Hinton, Geoffrey E., Nitish Srivastava, Alex Krizhevsky, Ilya Sutskever, and Ruslan Salakhutdinov. 2012. “Improving Neural Networks by Preventing Co-Adaptation of Feature Detectors.” CoRR abs/1207.0580. http://arxiv.org/abs/1207.0580.

Russell, Stuart, and Peter Norvig. 2020. Artificial Intelligence: A Modern Approach. 4th ed. Pearson. http://aima.cs.berkeley.edu/.

Marcel Turcotte

[email protected]

School of Electrical Engineering and Computer Science (EECS)

University of Ottawa