Neural Networks Architectures

CSI 4106 - Fall 2025

Marcel Turcotte

Version: Oct 28, 2025 20:58

Preamble

Message of the Day

Andrej Karpathy is a Slovak-Canadian computer scientist born in 1986 in Bratislava, who moved to Toronto with his family at the age of 15. He obtained a bachelor’s degree in computer science and physics from the University of Toronto (2009) and a master’s degree from the University of British Columbia (2011), where he worked with his advisor Michiel van de Panne on learning controllers for physically simulated figures. He then completed a Ph.D. at Stanford University under the supervision of Fei-Fei Li, focusing on the intersection of computer vision and natural language processing.

• Founding member and researcher at OpenAI (2015 – 2017).
• Senior Director of AI and Autopilot Vision at Tesla, Inc. (2017 – 2022).
• Returned to OpenAI in 2023 to lead a small team working on improving models (notably GPT-4), before leaving the company in 2024.
• Founder of Eureka Labs (since 2024), a startup focused on AI and education.

Will transformers drive AI in 10 years?, Andrej Karpathy, 2025-10-27.

Learning objectives

• Explain the Hierarchy of Concepts in Deep Learning
• Understand Convolution Operations Using Kernels
• Describe the Structure and Function of Convolutional Neural Networks (CNNs)
• Explain Receptive Fields, Padding, and Stride in CNNs
• Discusss the Role and Benefits of Pooling Layer

In the previous lecture, we examined the backpropagation algorithm, which provides a systematic method for calculating the partial derivatives of the loss function. This calculation is essential for applying the gradient descent algorithm, thus enabling the adjustment of weights in a deep neural network. Today, we will cover an intensive program. We will now discuss convolutional neural networks, which is a technology that continues to be impactful.

The study of convolutional networks involves multiple levels of complexity. Please feel free to ask questions if you need clarification.

Detailed learning objectives.

1. Softmax Layer:

• Describe its functionality in converting logits into probability distributions for classification tasks.

2. Cross-Entropy Loss:

• Explain its role in measuring the dissimilarity between predicted and true probability distributions.

3. Regularization Techniques:

• Explore methods like L1, L2 regularization, and dropout to enhance neural networks’ generalization capabilities.

4. Explain the Hierarchy of Concepts in Deep Learning

• Understand how deep learning models build hierarchical representations of data.
• Recognize how this hierarchy reduces the need for manual feature engineering.

5. Compare Deep and Shallow Neural Networks

• Discuss why deep networks are more parameter-efficient than shallow networks.
• Explain the benefits of depth in neural network architectures.

6. Describe the Structure and Function of Convolutional Neural Networks (CNNs)

• Understand how CNNs detect local patterns in data.
• Explain how convolutional layers reduce the number of parameters through weight sharing.

7. Understand Convolution Operations Using Kernels

• Describe how kernels (filters) are applied over input data to perform convolutions.
• Explain how feature maps are generated from convolution operations.

8. Explain Receptive Fields, Padding, and Stride in CNNs

• Define the concept of a receptive field in convolutional layers.
• Understand how padding and stride affect the output dimensions and computation.

9. Discuss the Role and Benefits of Pooling Layers

• Explain how pooling layers reduce spatial dimensions and control overfitting.
• Describe how pooling introduces translation invariance in CNNs.

What do you see?

import numpy as np
import matplotlib.pyplot as plt
from skimage import data, transform
from skimage.util import img_as_float

# Load a sample image (Chelsea the cat)
image = img_as_float(data.chelsea())

# Define transformations
def translate(image, tx=50, ty=30):
    tform = transform.AffineTransform(translation=(tx, ty))
    return transform.warp(image, tform.inverse)

def rotate(image, angle=30):
    return transform.rotate(image, angle, resize=True)

def shear(image, shear_deg=15):
    shear_rad = np.deg2rad(shear_deg)
    tform = transform.AffineTransform(shear=shear_rad)
    return transform.warp(image, tform.inverse)

# Apply transformations
rotated = rotate(image, 30)
translated = translate(image, 60, 30)
sheared = shear(image, 15)

# Create 2x2 grid
fig, axes = plt.subplots(2, 2, figsize=(5, 5))
axes = axes.ravel()
titles = ['Original', 'Rotated (30°)', 'Translated (60, 30)', 'Sheared (15°)']
images = [image, rotated, translated, sheared]

for ax, img, title in zip(axes, images, titles):
    ax.imshow(img)
    ax.set_title(title)
    ax.axis('off')

plt.tight_layout()
plt.show()

Even though these images look quite different in pixel space, you can still recognize the cat. A convolutional neural network learns filters that are robust to these transformations — that’s why it’s so powerful for vision tasks.

Convolution

Hierarchy of concepts

In the book “Deep Learning” (Goodfellow, Bengio, and Courville 2016), authors Goodfellow, Bengio, and Courville define deep learning as a subset of machine learning that enables computers to “understand the world in terms of a hierarchy of concepts.”

This hierarchical approach is one of deep learning’s most significant contributions. It reduces the need for manual feature engineering and redirects the focus toward the engineering of neural network architectures.

Convolutional Neural Networks (CNNs) have had a profound impact on the field of machine learning, particularly in areas involving image and video processing.

1. Revolutionizing Image Recognition: CNNs have significantly advanced the state of the art in image recognition and classification, achieving high accuracy across various datasets. This has led to breakthroughs in fields such as medical imaging, autonomous vehicles, and facial recognition.

2. Feature Extraction: CNNs automatically learn to extract features from raw data, eliminating the need for manual feature engineering. This capability has been crucial in handling complex data patterns and has expanded the applicability of machine learning to diverse domains.

3. Transfer Learning: CNNs facilitate transfer learning, where pre-trained networks on large datasets can be fine-tuned for specific tasks with limited data. This has made CNNs accessible and effective for a wide range of applications beyond their original training scope.

4. Advancements in Deep Learning: The success of CNNs has spurred further research in deep learning architectures, inspiring the development of more sophisticated models like recurrent neural networks (RNNs), long short-term memory networks (LSTMs), and transformer models.

5. Broader Application Areas: Beyond image processing, CNNs have been adapted for natural language processing, audio processing, and even in bioinformatics for tasks such as protein structure prediction and genomics.

6. Implications for Real-World Applications: CNNs have enabled practical applications in fields such as healthcare, where they assist in diagnostic imaging, and in security, where they enhance surveillance systems. They have also contributed to advancements in virtual reality, gaming, and augmented reality.

We have explored k-nearest neighbors algorithms and decision trees to provide you with a broader perspective on machine learning, which is not limited to neural networks alone. Currently, we are studying convolutional neural networks to illustrate the diversity of existing architectures in this field. Although it is impossible to cover all aspects in detail, our aim is to provide you with a solid understanding of the different paradigms of machine learning.

Attribution: LeCun, Bengio, and Hinton (2015)

Hierarchy of concepts

• Each layer detects patterns from the output of the layer preceding it.
  • In other words, proceeding from the input to the output of the network, the network uncovers “patterns of patterns”.
    • Analyzing an image, the networks first detect simple patterns, such as vertical, horizontal, diagonal lines, arcs, etc.
    • These are then combined to form corners, crosses, etc.
• (This explains how transfer learning works and why selecting the bottom layers only.)

But also …

“An MLP with just one hidden layer can theoretically model even the most complex functions, provided it has enough neurons. But for complex problems, deep networks have a much higher parameter efficiency than shallow ones: they can model complex functions using exponentially fewer neurons than shallow nets, allowing them to reach much better performance with the same amount of training data.”

During the lecture, attempt to discern why convolutional neural networks possess fewer parameters compared to fully connected feedforward networks.

Géron (2019) § 10

How many layers?

• Start with one layer, then increase the number of layers until the model starts overfitting the training data.
• Finetune the model adding regularization (dropout layers, regularization terms, etc.).

The number of neurons and other hyperparameters are determined using a grid search.

Observation

Consider a feed-forward network (FFN) and its model:

\[ h_{W,b}(X) = \phi_k(\ldots \phi_2(\phi_1(X)) \ldots) \]

where

\[ \phi_l(Z) = \sigma(W_l Z + b_l) \]

for \(l=1 \ldots k\). - The number of parameters in grows rapidly:

\[ (\text{size of layer}_{l-1} + 1) \times \text{size of layer}_{l} \]

Two layers 1,000-unit implies 1,000,000 parameters!

Image Classification Task

• Consider an RGB image with dimensions \(224 \times 224\), which is relatively small by contemporary benchmarks.
• The image consists of \(224 \times 224 \times 3 = 150,528\) input features.
• A neural network with merely a single hidden dense layer would require over 22,658,678,784 (22 billion) parameters, highlighting the computational complexity involved.

Convolutional Neural Network (CNN)

An excellent high-level overview of CNNs.

Convolutional Neural Network (CNN)

• Crucial pattern information is often local.

  • e.g., edges, corners, crosses.

• Convolutional layers reduce parameters significantly.

  • Unlike dense layers, neurons in a convolutional layer are not fully connected to the preceding layer.

  • Neurons connect only within their receptive fields (rectangular regions).

Convolutional networks originate from the domain of machine vision, which explains their intrinsic compatibility with grid-structured inputs.

The original publication by Yann Lecun has been cited nearly 35,000 times (Lecun et al. 1998).

Kernel

Kernel

A kernel is a small matrix, usually \(3 \times 3\), \(5 \times 5\), or similar in size, that slides over the input data (such as an image) to perform convolution.

Kernel

The detailed computational process will be elaborated upon subsequently. At this stage, it is sufficient to observe that the kernel is systematically traversed across the input matrix, generating a distinct output with each iteration.

Beginning with the kernel positioned to overlap the upper-left corner of the input matrix.

Kernel

It can be moved to the right three times.

Kernel

Kernel

Kernel

How many placements of the kernel over the input matrix are there? \(4 \times 4 = 16\).

The kernel can then be moved to the second row of the input matrix, and moved to the right three times.

Kernel Placements

Kernel

With the kernel placed over a specific region of the input matrix, the convolution is element-wise multiplication (each element of the kernel is multiplied by the corresponding element of the input matrix region it overlaps) followed by a summation of the results to produce a single scalar value.

Kernel

\(1 \times 1 + 2 \times 0 + 3 \times (-1) + 6 \times 1 + 5 \times 0 + 4 \times (-1) + 1 \times 1 + 2 \times 0 + 3 \times (-1) = -2\)

Kernel

It is referred to as a feature map because these outputs serve as features for the subsequent layer. In CNNs, the term “feature map” refers to the output of a convolutional layer after applying filters to the input data. These feature maps capture various patterns or features from the input, such as edges or textures in image data.

The output feature maps of one layer become the input for the next layer, effectively serving as features that the subsequent layer can use to learn more complex patterns. This hierarchical feature extraction process is a key characteristic of CNNs, allowing them to build progressively more abstract and high-level representations of the input data as the network depth increases.

The 16 resulting values can be organized into an output matrix. The element at position (0,0) in this output matrix represents the result of applying the convolution operation with the kernel at the initial position on the input matrix. In convolutional neural networks, the output matrix is referred to as a feature map.

Blurring

import numpy as np
from PIL import Image
import matplotlib.pyplot as plt
from scipy.ndimage import convolve

def apply_kernel_to_image(image_path, kernel):
    # Load the image and convert it to grayscale
    image = Image.open(image_path).convert('L')
    image_array = np.array(image)

    # Apply the convolution using the provided kernel
    convolved_array = convolve(image_array, kernel, mode='reflect')

    # Convert the convolved array back to an image
    convolved_image = Image.fromarray(convolved_array)

    # Display the original and convolved images
    plt.figure(figsize=(10, 4))

    plt.subplot(1, 2, 1)
    plt.title('Original Image')
    plt.imshow(image_array, cmap='gray')
    plt.axis('off')

    plt.subplot(1, 2, 2)
    plt.title('Convolved Image')
    plt.imshow(convolved_image, cmap='gray')
    plt.axis('off')

    plt.tight_layout()
    plt.show()

# Define the 3x3 averaging kernel
kernel = np.array([
    [1/9, 1/9, 1/9],
    [1/9, 1/9, 1/9],
    [1/9, 1/9, 1/9]
])

# Apply the kernel to the image (provide your image path here)
image_path = '../../assets/images/uottawa_hor_black.png'
apply_kernel_to_image(image_path, kernel)

# Define the 3x3 averaging kernel

kernel = np.array([
    [1/9, 1/9, 1/9],
    [1/9, 1/9, 1/9],
    [1/9, 1/9, 1/9]
])

The application of kernels to images has been a longstanding practice in the field of image processing.

A pixel is transformed into the average of itself and its eight surrounding neighbors, resulting in a blurred effect on the image.

Vertical Edge detection

# Define the 3x3 averaging kernel

kernel = np.array([
    [-0.25, 0, 0.25],
    [-0.25, 0, 0.25],
    [-0.25, 0, 0.25]
])

This is a type of edge detection kernel, specifically a horizontal gradient filter or a Sobel operator. It’s designed to detect changes in intensity along the horizontal axis, emphasizing vertical edges in an image.

When this kernel is convolved with an image:

• It highlights vertical edges by calculating the difference in pixel intensity between the left and right sides of a point.
• The negative values (-1) on the left subtract intensity, while the positive values (1) on the right add intensity, effectively measuring the horizontal gradient.
• The zeros in the middle ignore the central pixel’s contribution, focusing only on the contrast between left and right neighbors.

The result is an image where:

• Vertical edges (e.g., the boundary between a dark object and a light background) appear bright or dark, depending on the direction of the intensity change.
• Horizontal edges or uniform areas tend to be suppressed (close to zero).

Imagine sliding this kernel over an image like a scanner. For each pixel:

• It looks at the pixels to its left (subtracting their value with -1) and to its right (adding their value with 1).

• If the left and right sides are similar (e.g., same color), the result is near zero (no edge).

• If the left is dark and the right is light (or vice versa), the result is a strong positive or negative value, showing a vertical edge.

This is useful in computer vision (like in Tesla’s CNNs) to help detect object boundaries or lane lines by emphasizing where pixel values change sharply in the horizontal direction.

This kernel detects vertical edges by emphasizing differences in intensity between adjacent columns. It subtracts pixel values on the left from those on the right, enhancing vertical transitions and suppressing uniform regions.

Horizontal Edge detection

# Define the 3x3 averaging kernel

kernel = np.array([
    [-0.25, -0.25, -0.25],
    [0, 0, 0],
    [0.25, 0.25, 0.25]
])

This kernel detects horizontal edges by highlighting differences in intensity between adjacent rows. It subtracts pixel values in the upper row from those in the lower row, accentuating horizontal transitions while minimizing uniform areas.

Convolutions in Image Processing

Uses the Julia programming language.

But what is a convolution?

Convolution extending beyond its application in image processing.

Kernels

In contrast to image processing, where kernels are manually defined by the user, in convolutional networks, the kernels are automatically learned by the network.

To be continued \(\ldots\)

Receptive field

Receptive field

Attribution: Géron (2019) Figure 14.2

Receptive field

• Each unit is connected to neurons in its receptive fields.
  • Unit \(i,j\) in layer \(l\) is connected to the units \(i\) to \(i+f_h-1\), \(j\) to \(j+f_w-1\) of the layer \(l-1\), where \(f_h\) and \(f_w\) are respectively the height and width of the receptive field.

Padding

Zero padding. In order to have layers of the same size, the grid can be padded with zeros.

Padding

No padding

Half padding

Full padding

Attribution: github.com/vdumoulin/conv_arithmetic

Stride

Stride. It is possible to connect a larger layer \((l-1)\) to a smaller one \((l)\) by skipping units. The number of units skipped is called stride, \(s_h\) and \(s_w\).

• Unit \(i,j\) in layer \(l\) is connected to the units \(i \times s_h\) to \(i \times s_h + f_h - 1\), \(j \times s_w\) to \(j \times s_w + f_w - 1\) of the layer \(l-1\), where \(f_h\) and \(f_w\) are respectively the height and width of the receptive field, \(s_h\) and \(s_w\) are respectively the height and width strides.

Stride

No padding, strides

Padding, strides

Attribution: github.com/vdumoulin/conv_arithmetic

Filters

Filters

• A window of size \(f_h \times f_w\) is moved over the output of layers \(l-1\), referred to as the input feature map, position by position.

• For each location, the product is calculated between the extracted patch and a matrix of the same size, known as a convolution kernel or filter. The sum of the values in the resulting matrix constitutes the output for that location.

Model

Model

\[ z_{i,j,k} = b_k + \sum_{u=0}^{f_h-1} \sum_{v=0}^{f_w-1} \sum_{k'=0}^{f_{n'}-1} x_{i',j',k'} \cdot w_{u,v,k',k} \]

where \(i' = i \times s_h + u\) and \(j' = j \times s_w + v\).

Attribution: Géron (2019) Figure 14.6

Convolutional Layer

• “Thus, a layer full of neurons using the same filter outputs a feature map.”

• “Of course, you do not have to define the filters manually: instead, during training the convolutional layer will automatically learn the most useful filters for its task.”

Géron (2019) § 14

Convolutional Layer

• “(…) and the layers above will learn to combine them into more complex patterns.”

• “The fact that all neurons in a feature map share the same parameters dramatically reduces the number of parameters in the model.”

Géron (2019) § 14

Summmary

1. Feature Map: In convolutional neural networks (CNNs), the output of a convolution operation is known as a feature map. It captures the features of the input data as processed by a specific kernel.

Summmary

2. Kernel Parameters: The parameters of the kernel are learned through the backpropagation process, allowing the network to optimize its feature extraction capabilities based on the training data.

Summmary

3. Bias Term: A single bias term is added uniformly to all entries of the feature map. This bias helps adjust the activation level, providing additional flexibility for the network to better fit the data.

Summmary

4. Activation Function: Following the addition of the bias, the feature map values are typically passed through an activation function, such as ReLU (Rectified Linear Unit). The ReLU function introduces non-linearity by setting negative values to zero while retaining positive values, enabling the network to learn more complex patterns.

Pooling

Pooling

• A pooling layer exhibits similarities to a convolutional layer.

  • Each neuron in a pooling layer is connected to a set of neurons within a receptive field.

• However, unlike convolutional layers, pooling layers do not possess weights.

  • Instead, they produce an output by applying an aggregating function, commonly max or mean.

In a pooling layer, specifically max pooling, the max function is inherently nondifferentiable because it involves selecting the maximum value from a set of inputs. However, in the context of backpropagation in neural networks, we can work around this by using a concept known as the “gradient of the max function.”

Here’s how it is done:

1. Forward Pass: During the forward pass, the max pooling layer selects the maximum value from each pooling region (e.g., a 2x2 window) and passes these values to the next layer.

2. Backward Pass: During backpropagation, the gradient is propagated only to the input that was the maximum value in the forward pass. This means that the derivative is 1 for the position that held the maximum value and 0 for all other positions within the pooling window.

This approach effectively allows the max operation to participate in gradient-based optimization processes like backpropagation, even though the max function itself is nondifferentiable. By assigning the gradient to the position of the maximum value, the network can learn which features are most important for the task at hand.

Similar to convolutional layers, pooling layers allow specification of the receptive field size, padding, and stride. For the MaxPool2D function, the default receptive field size is \(2 \times 2\).

Pooling

• This subsampling process leads to a reduction in network size; each window of dimensions \(f_h \times f_w\) is condensed to a single value, typically the maximum or mean of that window.

• According to Géron (2019), a max pooling layer provides a degree of invariance to small translations (§ 14).

Pooling

1. Dimensionality Reduction: Pooling layers reduce the spatial dimensions (width and height) of the input feature maps. This reduction decreases the number of parameters and computational load in the network, which can help prevent overfitting.

Pooling

2. Feature Extraction: By summarizing the presence of features in a region, pooling layers help retain the most critical information while discarding less important details. This process enables the network to focus on the most salient features.

Pooling

3. Translation Invariance: Pooling introduces a degree of invariance to translations and distortions in the input. For instance, max pooling captures the most prominent feature in a local region, making the network less sensitive to small shifts or variations in the input.

Pooling

4. Noise Reduction: Pooling can help smooth out noise in the input by aggregating information over a region, thus emphasizing consistent features over random variations.

Pooling

5. Hierarchical Feature Learning: By reducing the spatial dimensions progressively through the layers, pooling layers allow the network to build a hierarchical representation of the input data, capturing increasingly abstract and complex features at deeper layers.

Keras

import tensorflow as tf
from functools import partial  

DefaultConv2D = partial(tf.keras.layers.Conv2D, kernel_size=3, padding="same", activation="relu", kernel_initializer="he_normal") 

model = tf.keras.Sequential([     
  DefaultConv2D(filters=64, kernel_size=7, input_shape=[28, 28, 1]), 
  tf.keras.layers.MaxPool2D(),     
  DefaultConv2D(filters=128),
  DefaultConv2D(filters=128),
  tf.keras.layers.MaxPool2D(),
  DefaultConv2D(filters=256),
  DefaultConv2D(filters=256),
  tf.keras.layers.MaxPool2D(),
  tf.keras.layers.Flatten(),
  tf.keras.layers.Dense(units=128, activation="relu", kernel_initializer="he_normal"),     
  tf.keras.layers.Dropout(0.5),
  tf.keras.layers.Dense(units=64, activation="relu", kernel_initializer="he_normal"),
  tf.keras.layers.Dropout(0.5),
  tf.keras.layers.Dense(units=10, activation="softmax") ])  

model.summary()

The previously discussed model, which comprised fully connected (Dense) layers, attained a test accuracy of 88%.

We will look at pooling next.

Géron (2022) Chapter 11, test accuracy of 92% on the Fashion-MNIST dataset

Keras

Model: "sequential_6"

┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type)                    ┃ Output Shape           ┃       Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ conv2d_30 (Conv2D)              │ (None, 28, 28, 64)     │         3,200 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ max_pooling2d_18 (MaxPooling2D) │ (None, 14, 14, 64)     │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ conv2d_31 (Conv2D)              │ (None, 14, 14, 128)    │        73,856 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ conv2d_32 (Conv2D)              │ (None, 14, 14, 128)    │       147,584 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ max_pooling2d_19 (MaxPooling2D) │ (None, 7, 7, 128)      │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ conv2d_33 (Conv2D)              │ (None, 7, 7, 256)      │       295,168 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ conv2d_34 (Conv2D)              │ (None, 7, 7, 256)      │       590,080 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ max_pooling2d_20 (MaxPooling2D) │ (None, 3, 3, 256)      │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ flatten_6 (Flatten)             │ (None, 2304)           │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_18 (Dense)                │ (None, 128)            │       295,040 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dropout_12 (Dropout)            │ (None, 128)            │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_19 (Dense)                │ (None, 64)             │         8,256 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dropout_13 (Dropout)            │ (None, 64)             │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_20 (Dense)                │ (None, 10)             │           650 │
└─────────────────────────────────┴────────────────────────┴───────────────┘

 Total params: 1,413,834 (5.39 MB)

 Trainable params: 1,413,834 (5.39 MB)

 Non-trainable params: 0 (0.00 B)

Convolutional Neural Networks

The architecture involves sequentially stacking several convolutional layers, each followed by a ReLU activation layer, and then a pooling layer. As this process continues, the spatial dimensions of the image representation decrease. Concurrently, the number of feature maps increases, as illustrated in our Keras example. At the top of this stack, a standard feedforward neural network is incorporated.

AlexNet

Krizhevsky, Sutskever, and Hinton (2012)

AlexNet consists of eight layers with learnable parameters: five convolutional layers followed by three fully connected layers. The architecture also includes max-pooling layers, ReLU activation functions, and dropout to improve training performance and reduce overfitting.

Attribution: Prince (2023)

VGG

Simonyan and Zisserman (2015)

Complementary information can be found here.

Convolutional networks (ConvNets) currently set the state of the art in visual recognition. The aim of this project is to investigate how the ConvNet depth affects their accuracy in the large-scale image recognition setting.

Our main contribution is a rigorous evaluation of networks of increasing depth, which shows that a significant improvement on the prior-art configurations can be achieved by increasing the depth to 16-19 weight layers, which is substantially deeper than what has been used in the prior art. To reduce the number of parameters in such very deep networks, we use very small 3×3 filters in all convolutional layers (the convolution stride is set to 1). Please see our publication for more details.

Attribution: Prince (2023)

ConvNets Performance

Attribution: Prince (2023)

StatQuest

The video presents a straightforward example that differentiates between images of the letter O and the letter X, utilizing a single filter for this purpose. This approach simplifies the explanation, making it easy to follow. In practical applications, however, each convolutional layer typically contains dozens or even hundreds of filters.

Final Word

As you might expect, the number of layers and filters are hyperparameters that are optimized through the process of hyperparameter tuning.

Attribution: @stefaan_cotteni

Prologue

Summary

• Hierarchy of Concepts in Deep Learning
• Kernels and Convolution Operations
• Receptive Field, Padding, and Stride
• Filters and Feature Maps
• Convolutional Layers
• Pooling Layers

Summary

• Hierarchy of Concepts in Deep Learning
  • Deep learning models represent data through layers of increasing abstraction.
  • Each layer learns patterns based on the outputs of preceding layers (“patterns of patterns”).
  • This hierarchical learning reduces reliance on manual feature engineering.
  • Deep networks achieve better performance with fewer parameters compared to shallow networks.
• Convolutional Neural Networks (CNNs)
  • CNNs specialize in processing data with a grid-like topology (e.g., images).
  • They detect local patterns using convolutional layers with shared weights.
  • Neurons in convolutional layers connect only within their receptive fields, not fully connected.
  • This local connectivity and weight sharing significantly reduce the number of parameters.
• Kernels and Convolution Operations
  • Kernels (filters) are small matrices that slide over the input data to perform convolutions.
  • The convolution operation involves element-wise multiplication and summation.
  • Kernels can be designed to detect specific features like edges and textures.
  • Feature maps are generated, highlighting where certain features are detected in the input.
• Receptive Field, Padding, and Stride
  • Receptive Field: The local region of the input that a neuron is sensitive to.
  • Padding: Adding zeros around the input to maintain spatial dimensions after convolution.
  • Stride: The step size with which the kernel moves over the input data.
  • These parameters control the output size and computation in convolutional layers.
• Filters and Feature Maps
  • Filters are learned during training and are crucial for feature detection.
  • All neurons in a feature map share the same filter parameters.
  • This sharing leads to efficient parameter usage and consistent feature detection across the input.
• Convolutional Layers
  • Perform convolutions followed by adding a bias term and applying an activation function (e.g., ReLU).
  • The activation function introduces non-linearity, allowing the network to learn complex patterns.
  • The use of shared weights and biases reduces the total number of parameters.
• Pooling Layers
  • Purpose: Reduce the spatial dimensions of feature maps to control overfitting and computation.
  • Types:
    • Max Pooling: Takes the maximum value within a pooling window.
    • Average Pooling: Computes the average value within a pooling window.
  • Benefits:
    • Dimensionality reduction leads to fewer parameters and faster computation.
    • Introduces translation invariance, making the network robust to shifts and distortions.
    • Helps in hierarchical feature learning by focusing on prominent features.
• Building CNN Architectures
  • CNNs are built by stacking convolutional and pooling layers.
  • Spatial dimensions decrease while the number of feature maps increases in deeper layers.
  • Often culminates with fully connected layers for classification tasks.
  • Example architectures can be implemented using frameworks like Keras.
• Hyperparameter Tuning
  • Key hyperparameters include the number of layers, filters, kernel sizes, strides, and padding.
  • Proper tuning is essential for achieving optimal model performance.
  • Overfitting can be controlled using techniques like dropout and regularization.
• Future Directions
  • Feature Attribution:
    • Techniques like saliency maps and activation maximization help interpret model decisions.
    • Essential for applications requiring explainability (e.g., self-driving cars).
  • Transfer Learning:
    • Involves using pre-trained models on new tasks to save time and resources.
    • Particularly useful when labeled data is scarce.

Future Directions

When integrating CNNs into your projects, consider exploring the following topics:

• Feature Attribution: Various techniques are available to visualize what the network has learned. For example, in the context of self-driving cars, it is crucial to ensure that the network focuses on relevant features, avoiding distractions.

• Transfer Learning: This approach enables the reuse of weights from pre-trained networks, which accelerates the learning process, reduces computational demands, and facilitates network training even with a limited number of examples.

There are also 1D convolutions, which are often applied in bioinformatics.

Further Reading

• Understanding Deep Learning (Prince 2023) is a recently published textbook focused on the foundational concepts of deep learning.

• It begins with fundamental principles and extends to contemporary topics such as transformers, diffusion models, graph neural networks, autoencoders, adversarial networks, and reinforcement learning.

• The textbook aims to help readers comprehend these concepts without delving excessively into theoretical details.

• It includes sixty-eight Python notebook exercises.

• The book follows a “read-first, pay-later” model.

Resources

• A guide to convolution arithmetic for deep learning
• Authors: Vincent Dumoulin and Francesco Visin
• Last revised: 11 Jan 2018
  • arXiv:1603.07285
  • GitHub Repository

Next lecture

• We will introduce solution spaces.

References

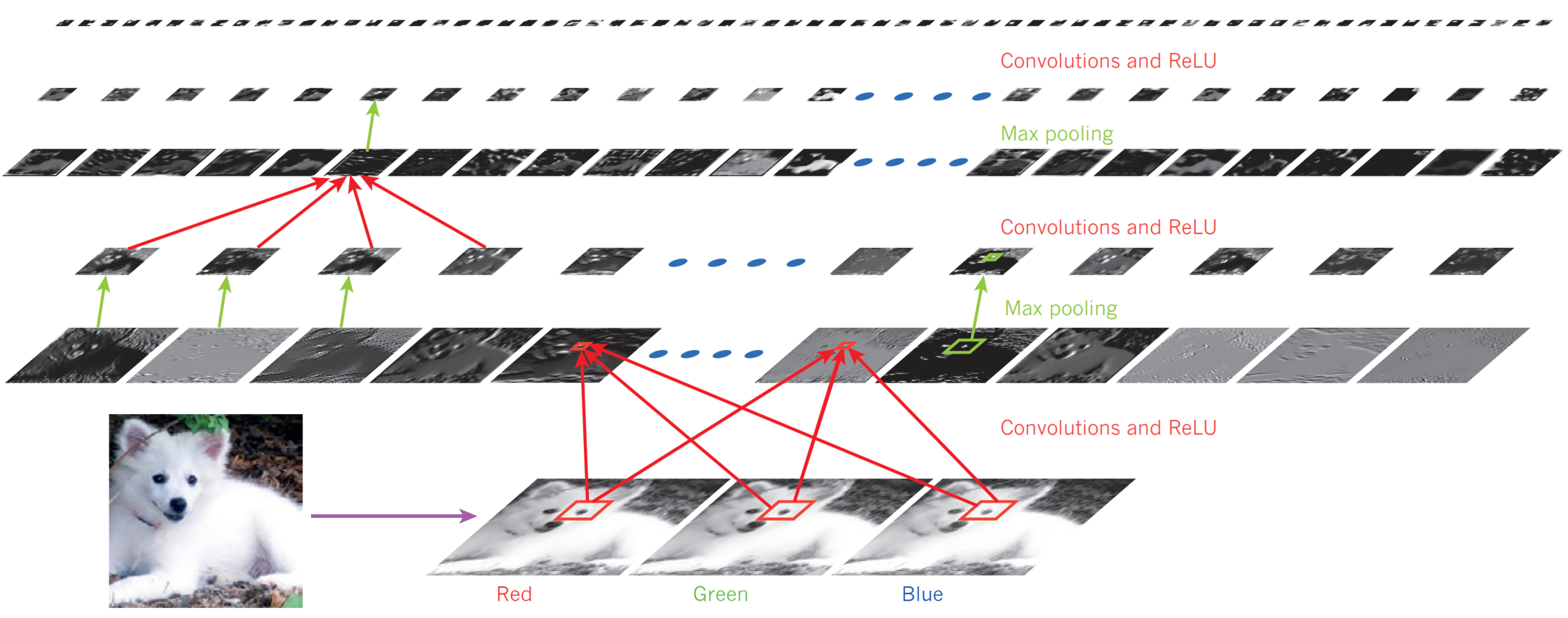
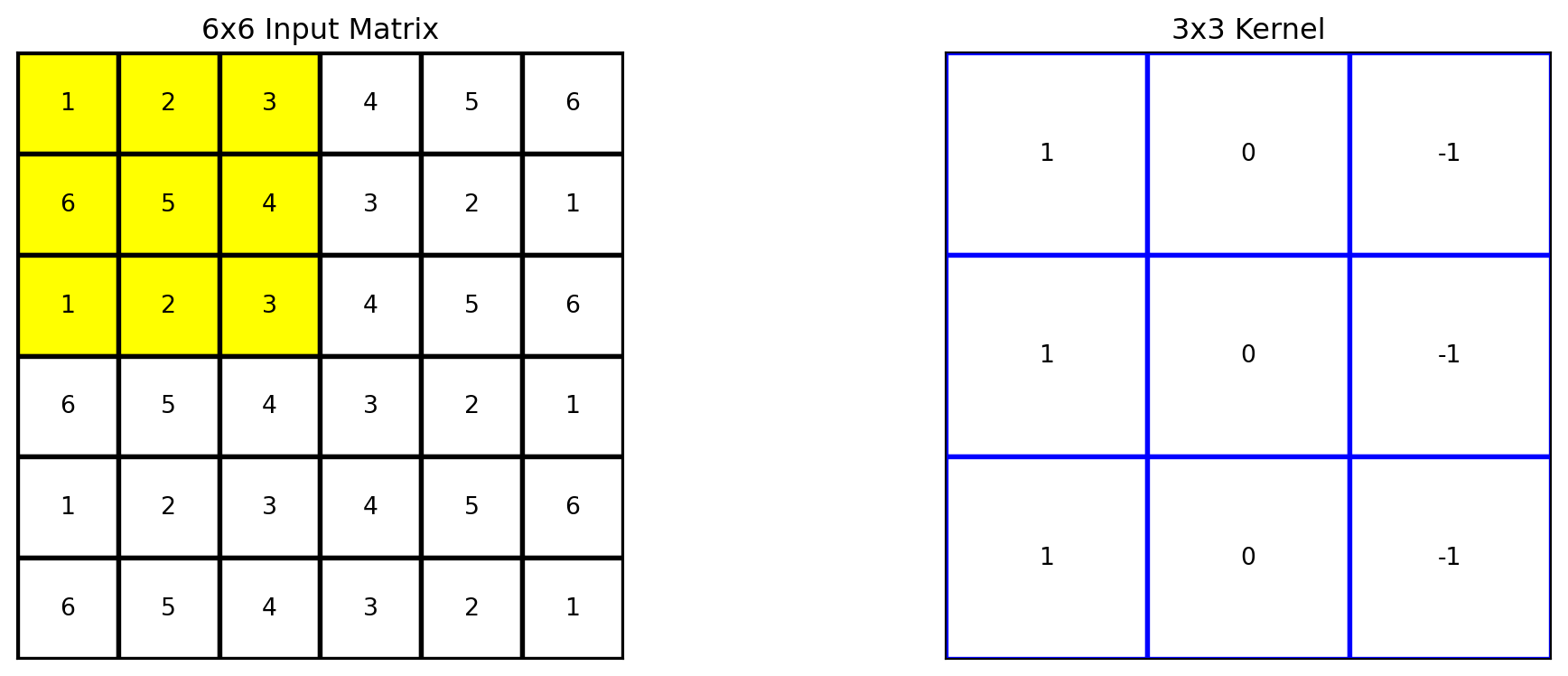
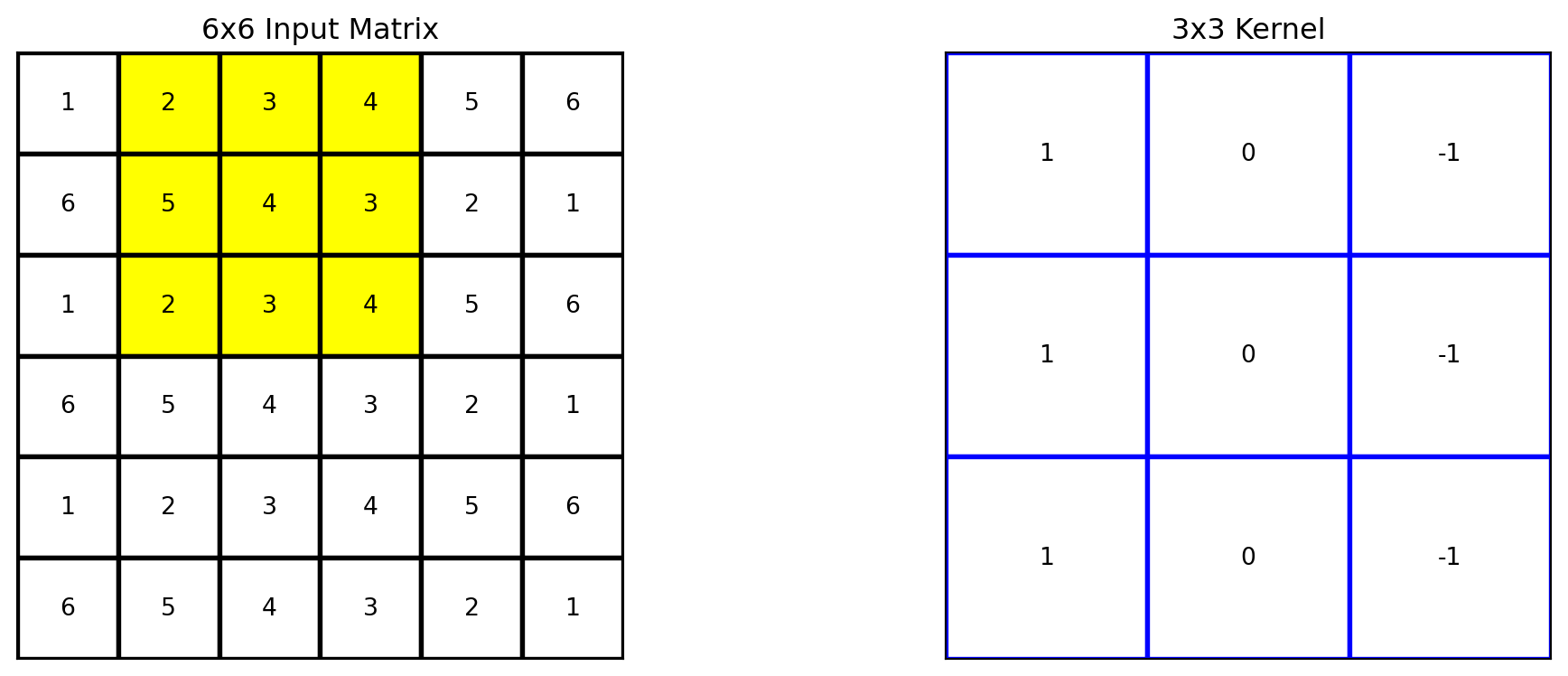
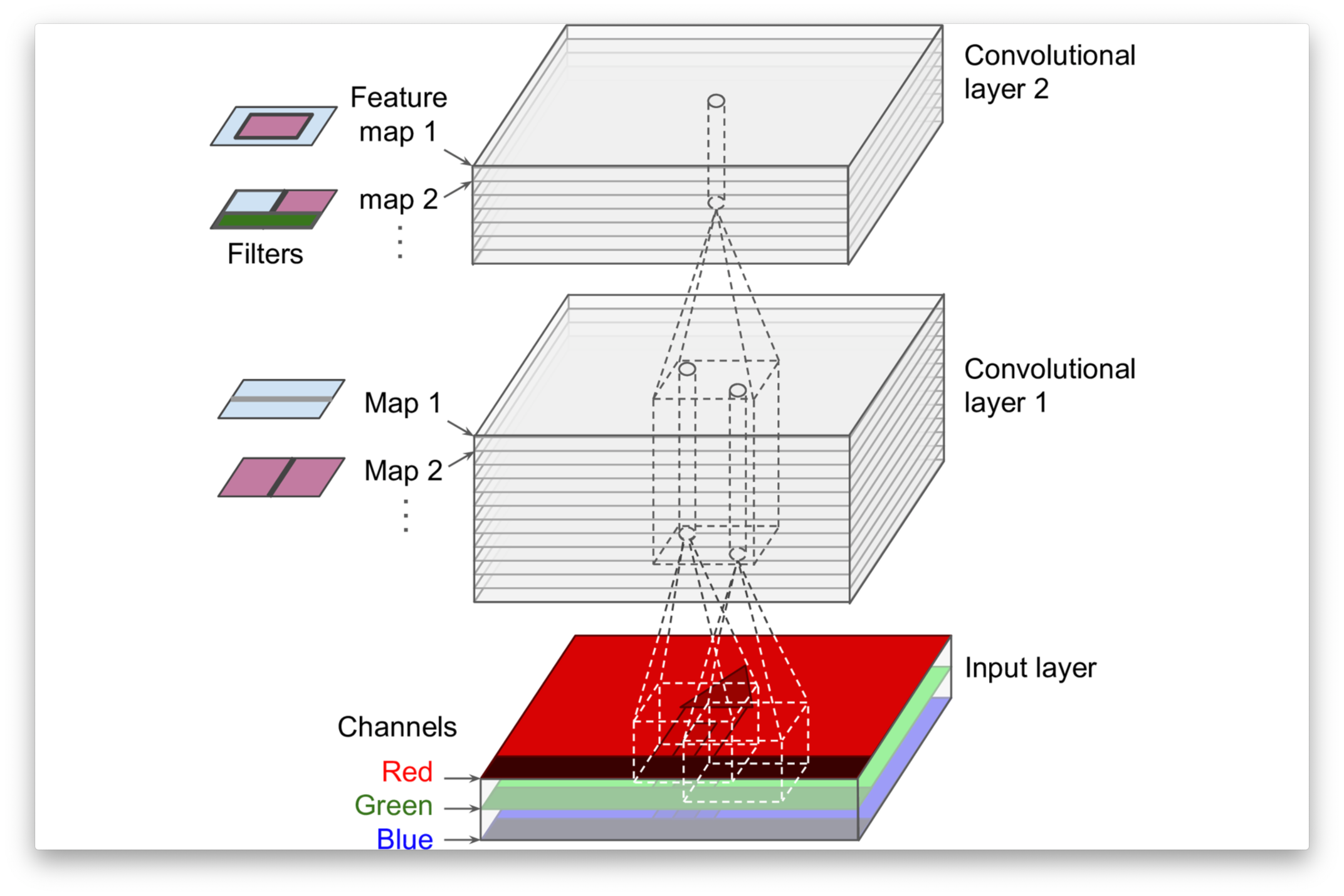
Géron, Aurélien. 2019. Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow. 2nd ed. O’Reilly Media.

———. 2022. Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow. 3rd ed. O’Reilly Media, Inc.

Goodfellow, Ian, Yoshua Bengio, and Aaron Courville. 2016. Deep Learning. Adaptive Computation and Machine Learning. MIT Press. https://dblp.org/rec/books/daglib/0040158.

Krizhevsky, Alex, Ilya Sutskever, and Geoffrey E Hinton. 2012. “ImageNet Classification with Deep Convolutional Neural Networks.” In Advances in Neural Information Processing Systems, edited by F. Pereira, C. J. Burges, L. Bottou, and K. Q. Weinberger. Vol. 25. Curran Associates, Inc. https://proceedings.neurips.cc/paper_files/paper/2012/file/c399862d3b9d6b76c8436e924a68c45b-Paper.pdf.

LeCun, Yann, Yoshua Bengio, and Geoffrey Hinton. 2015. “Deep Learning.” Nature 521 (7553): 436–44. https://doi.org/10.1038/nature14539.

Lecun, Y., L. Bottou, Y. Bengio, and P. Haffner. 1998. “Gradient-Based Learning Applied to Document Recognition.” Proceedings of the IEEE 86 (11): 2278–2324. https://doi.org/10.1109/5.726791.

Prince, Simon J. D. 2023. Understanding Deep Learning. The MIT Press. http://udlbook.com.

Russell, Stuart, and Peter Norvig. 2020. Artificial Intelligence: A Modern Approach. 4th ed. Pearson. http://aima.cs.berkeley.edu/.

Simonyan, Karen, and Andrew Zisserman. 2015. “Very Deep Convolutional Networks for Large-Scale Image Recognition.” In International Conference on Learning Representations.

Marcel Turcotte

Marcel.Turcotte@uOttawa.ca

School of Electrical Engineering and Computer Science (EECS)

University of Ottawa