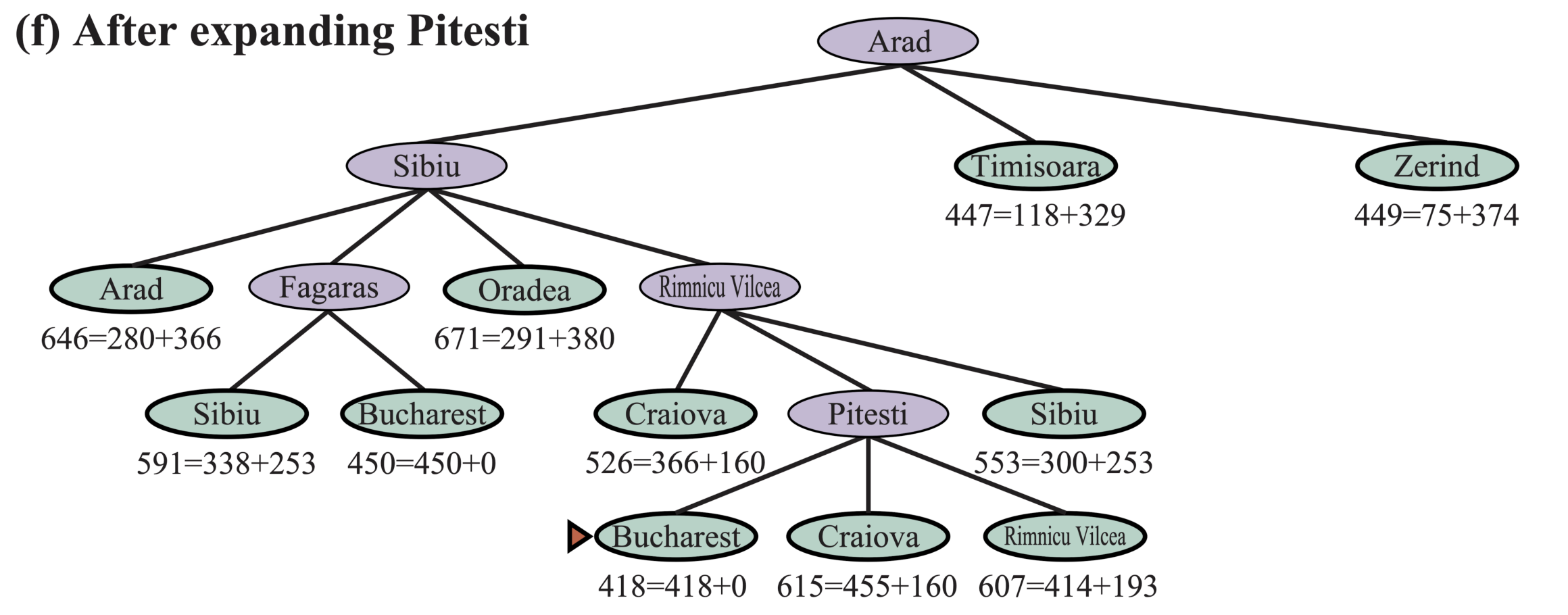
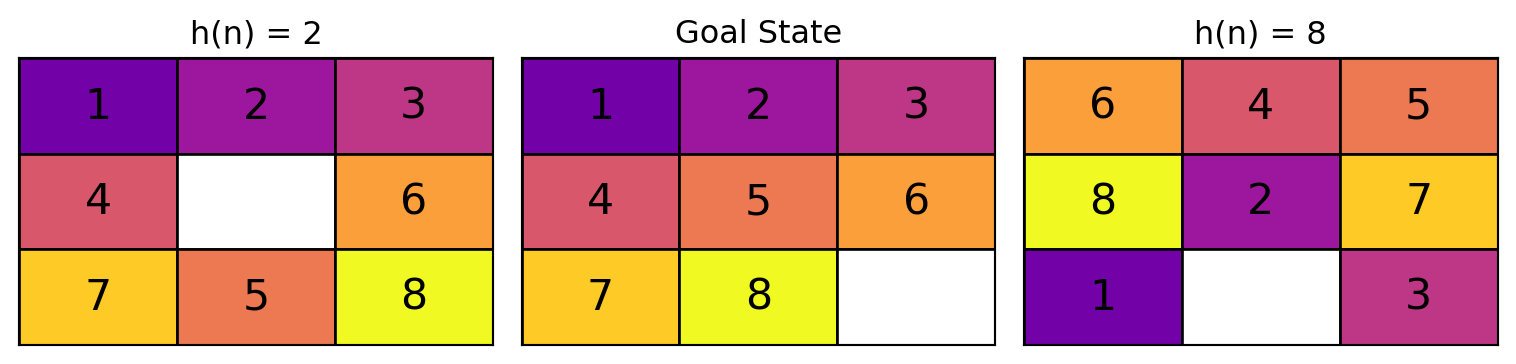
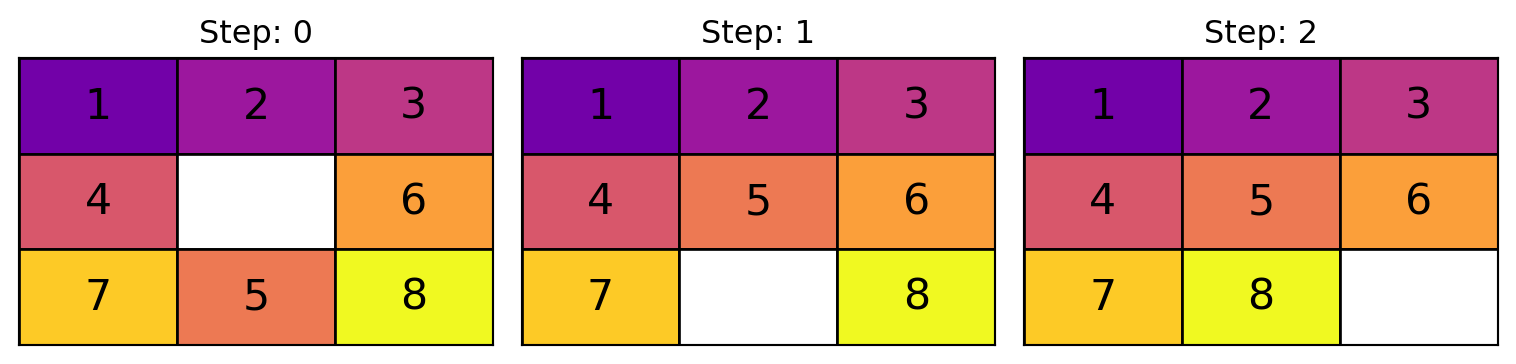
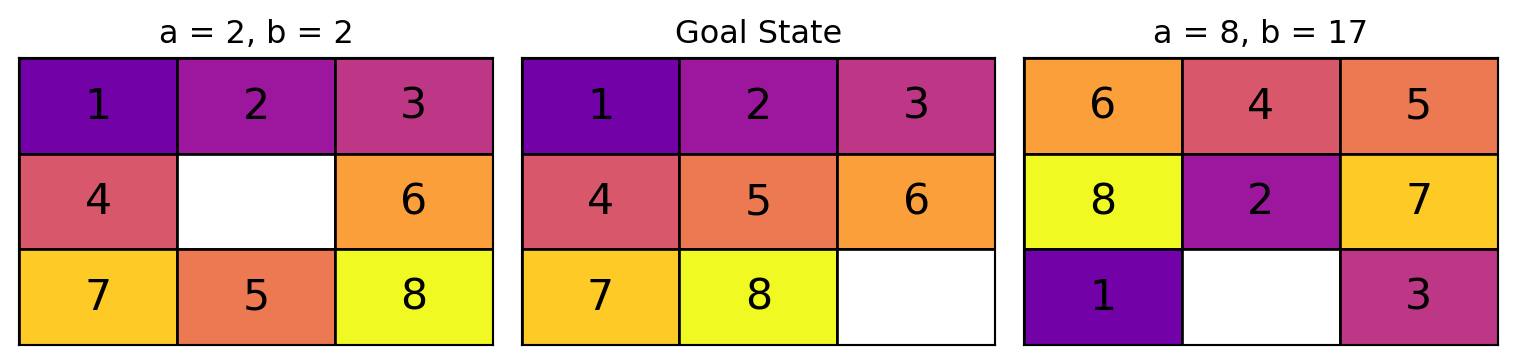
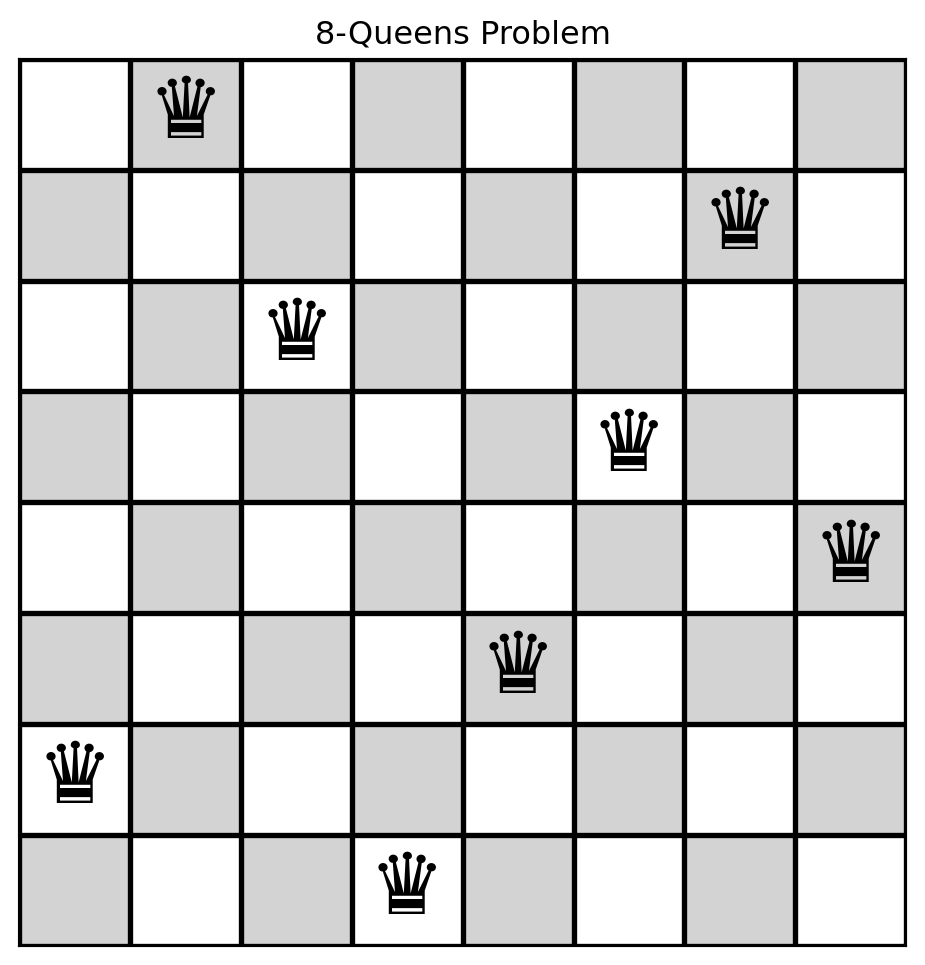
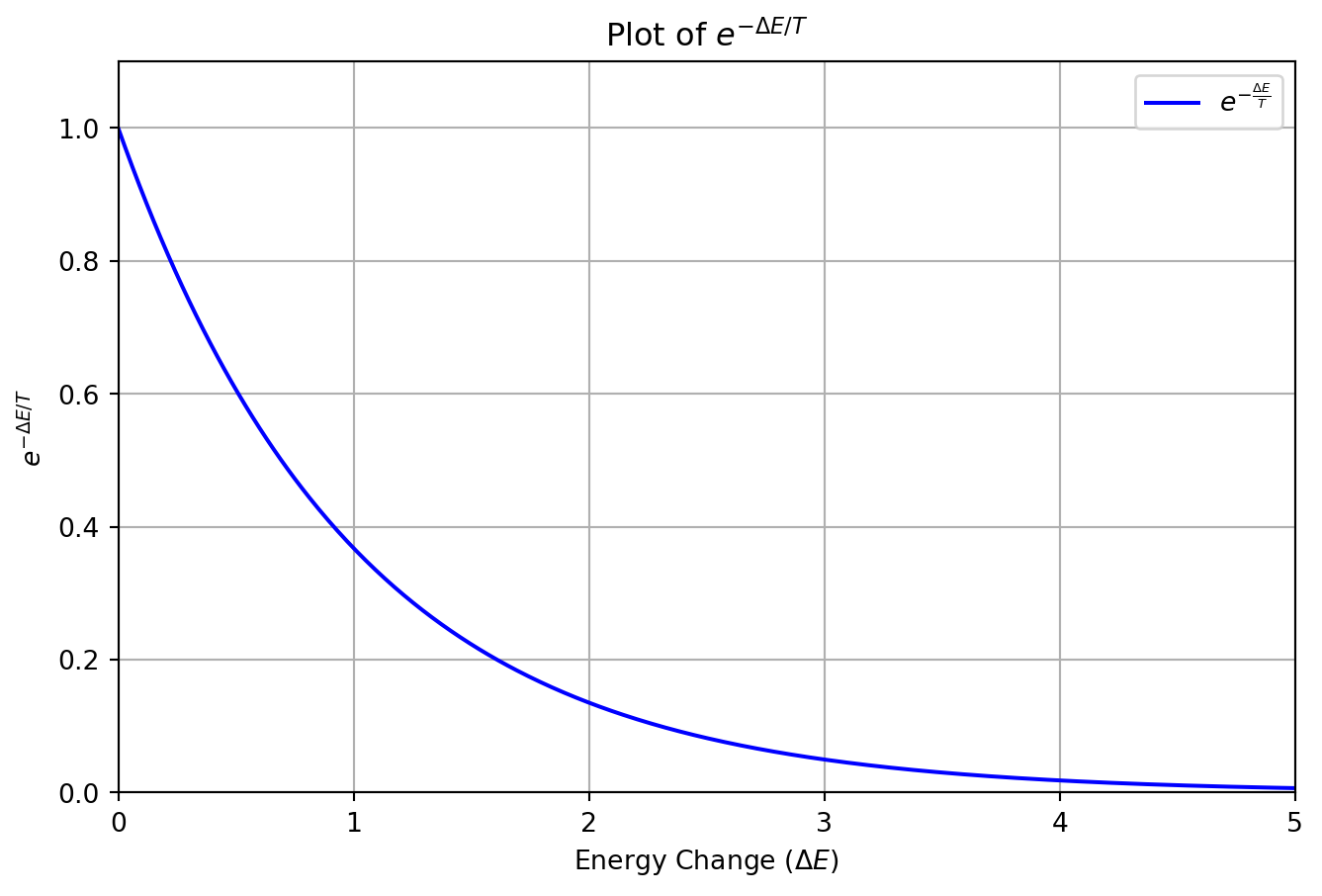
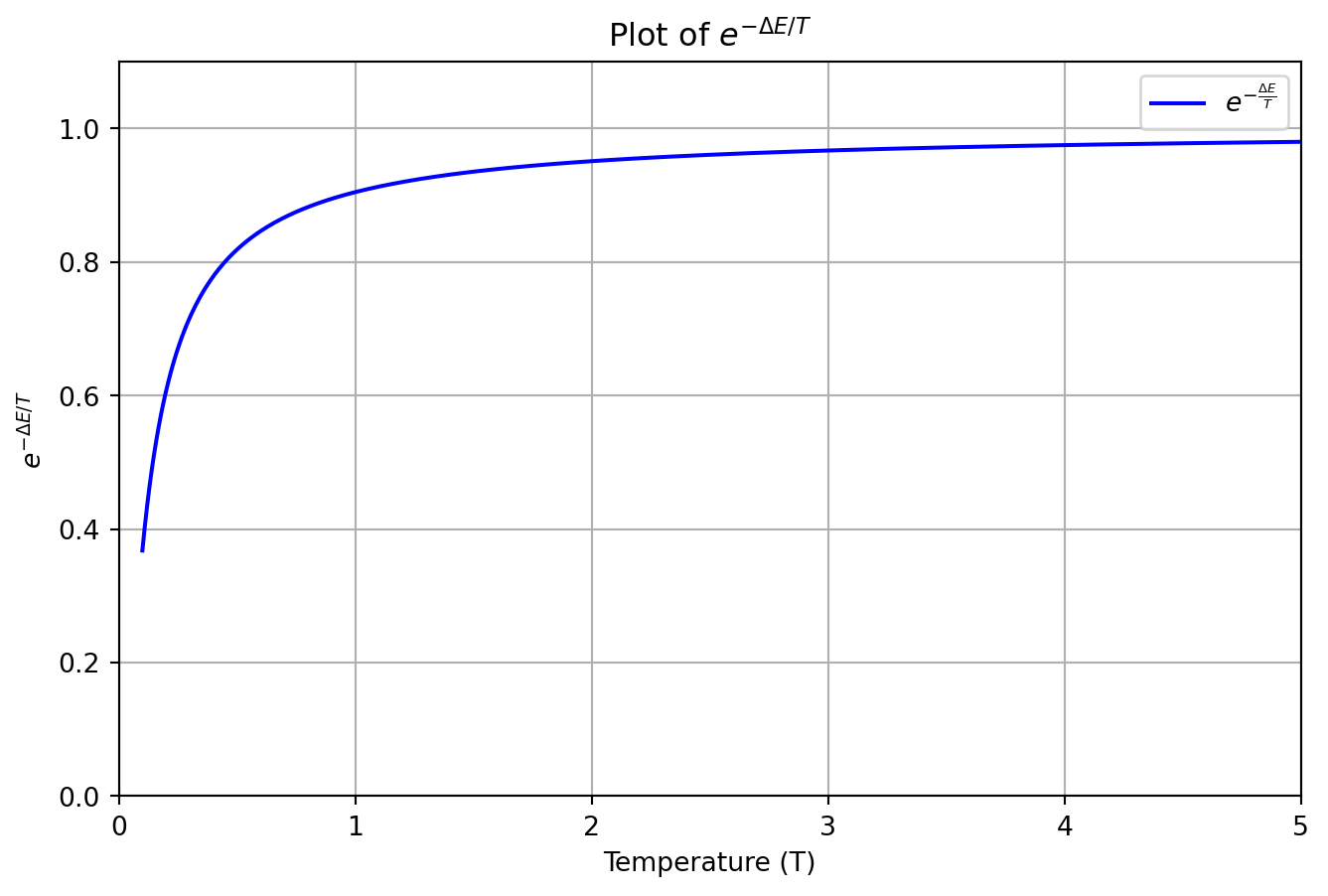
Code
import random
import matplotlib.pyplot as plt
import numpy as np
random.seed(58)
def is_solvable(tiles):
# Compter les inversions dans la liste à plat des tuiles (en excluant l'espace vide)
inversions = 0
for i in range(len(tiles)):
for j in range(i + 1, len(tiles)):
if tiles[i] != 0 and tiles[j] != 0 and tiles[i] > tiles[j]:
inversions += 1
return inversions % 2 == 0
def generate_solvable_board():
# Générer une configuration de plateau aléatoire qui est garantie d'être résoluble
tiles = list(range(9))
random.shuffle(tiles)
while not is_solvable(tiles):
random.shuffle(tiles)
return tiles
def plot_board(board, title, num_pos, position):
ax = plt.subplot(1, num_pos, position)
ax.set_title(title)
ax.set_xticks([])
ax.set_yticks([])
board = np.array(board).reshape(3, 3).tolist() # Reconfigurer en une grille 3x3
# Utiliser une carte de couleurs pour afficher les numéros
cmap = plt.cm.plasma
norm = plt.Normalize(vmin=-1, vmax=8)
for i in range(3):
for j in range(3):
tile_value = board[i][j]
color = cmap(norm(tile_value))
ax.add_patch(plt.Rectangle((j, 2 - i), 1, 1, facecolor=color, edgecolor='black'))
if tile_value == 0:
ax.add_patch(plt.Rectangle((j, 2 - i), 1, 1, facecolor='white', edgecolor='black'))
else:
ax.text(j + 0.5, 2 - i + 0.5, str(tile_value),
fontsize=16, ha='center', va='center', color='black')
ax.set_xlim(0, 3)
ax.set_ylim(0, 3)