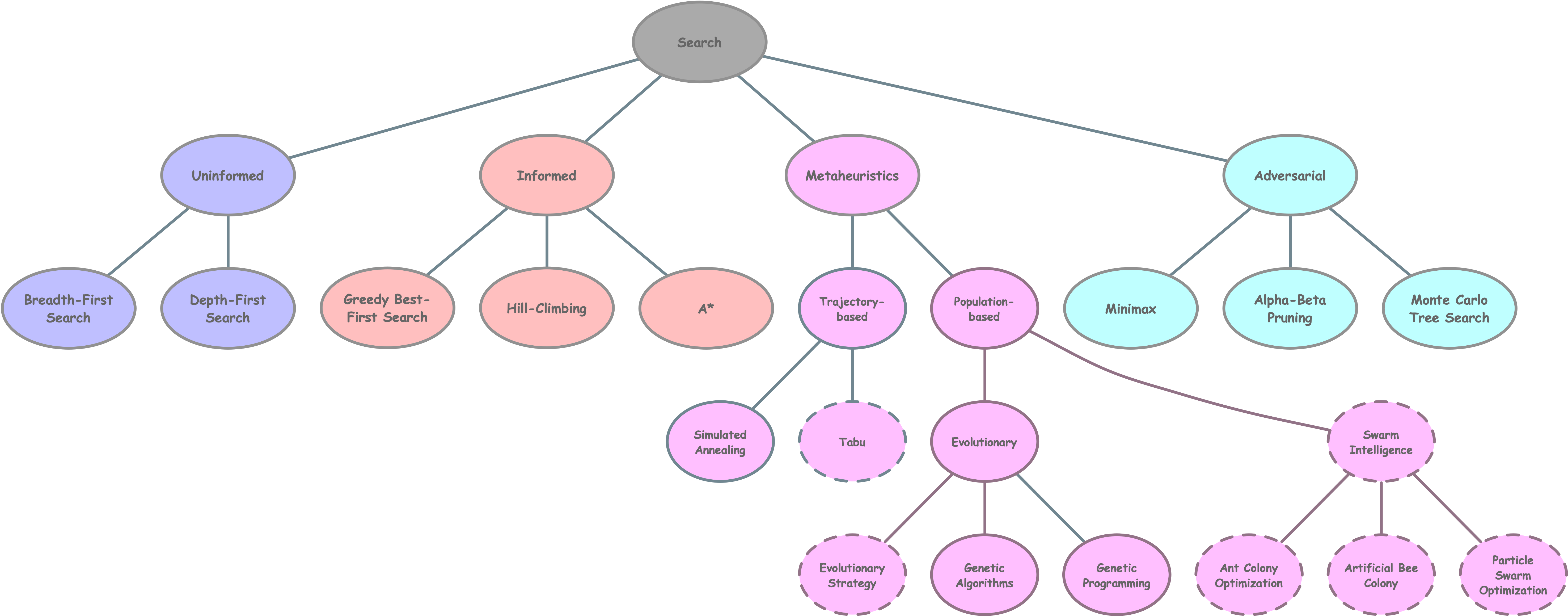
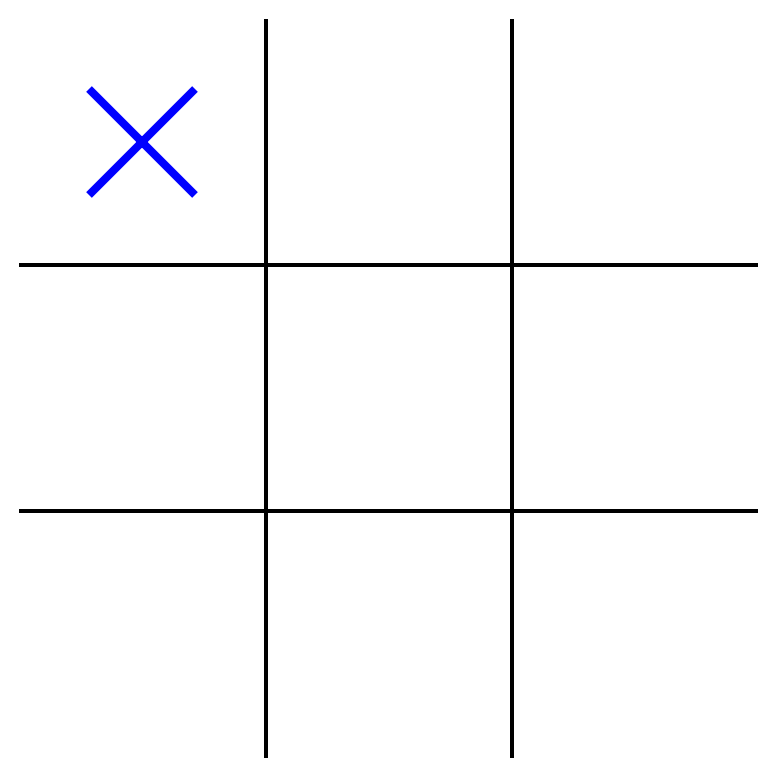
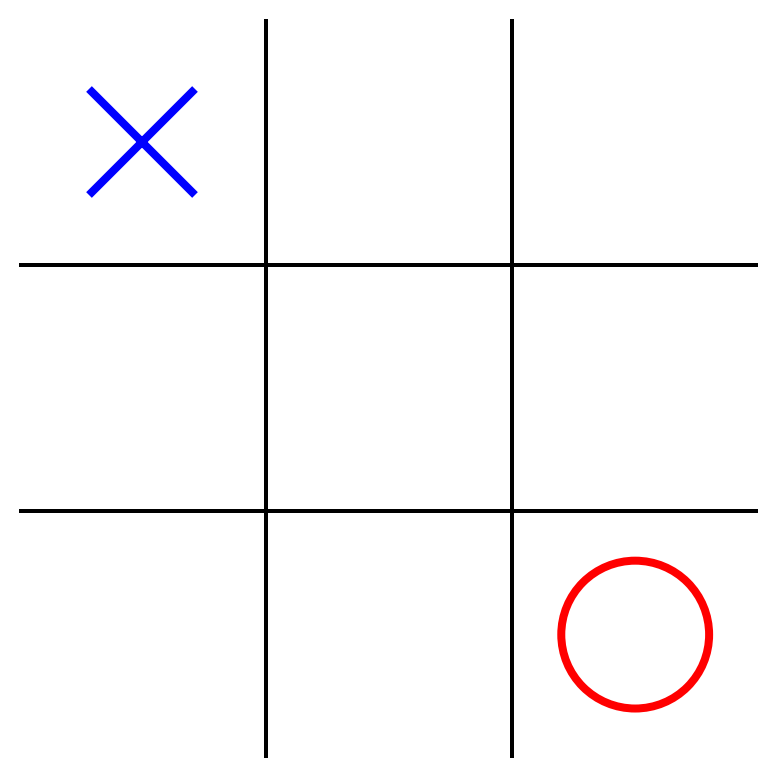
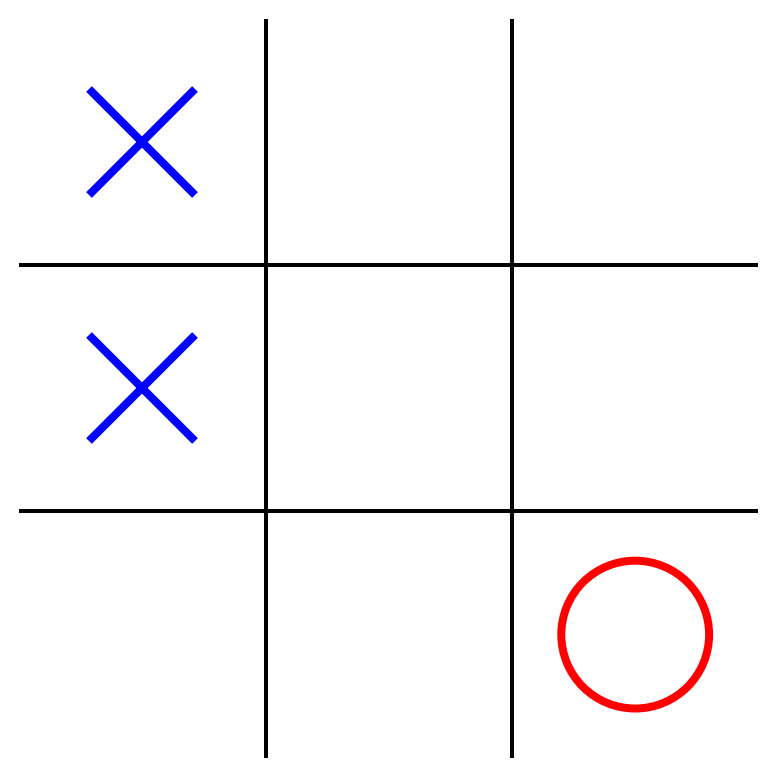
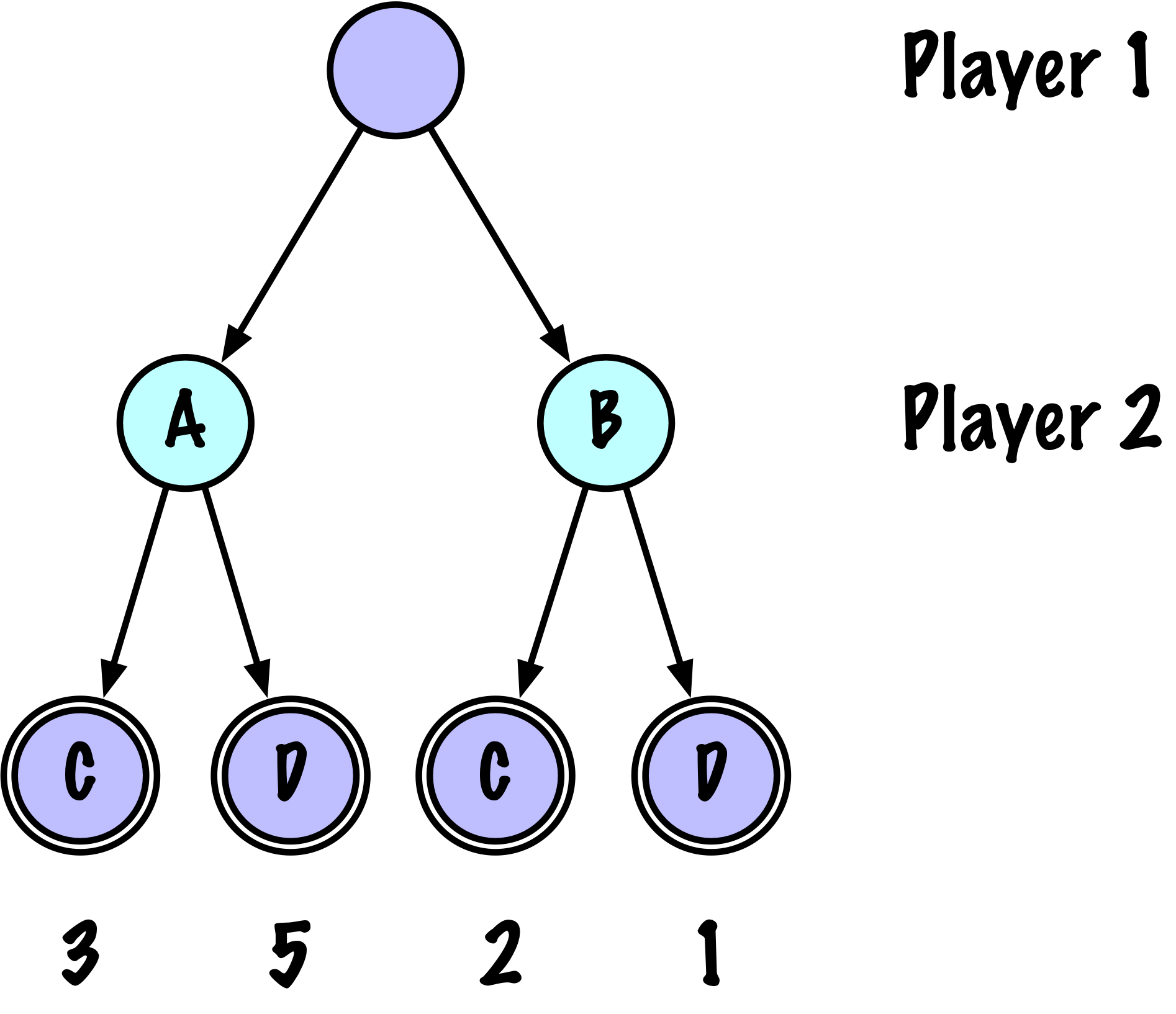
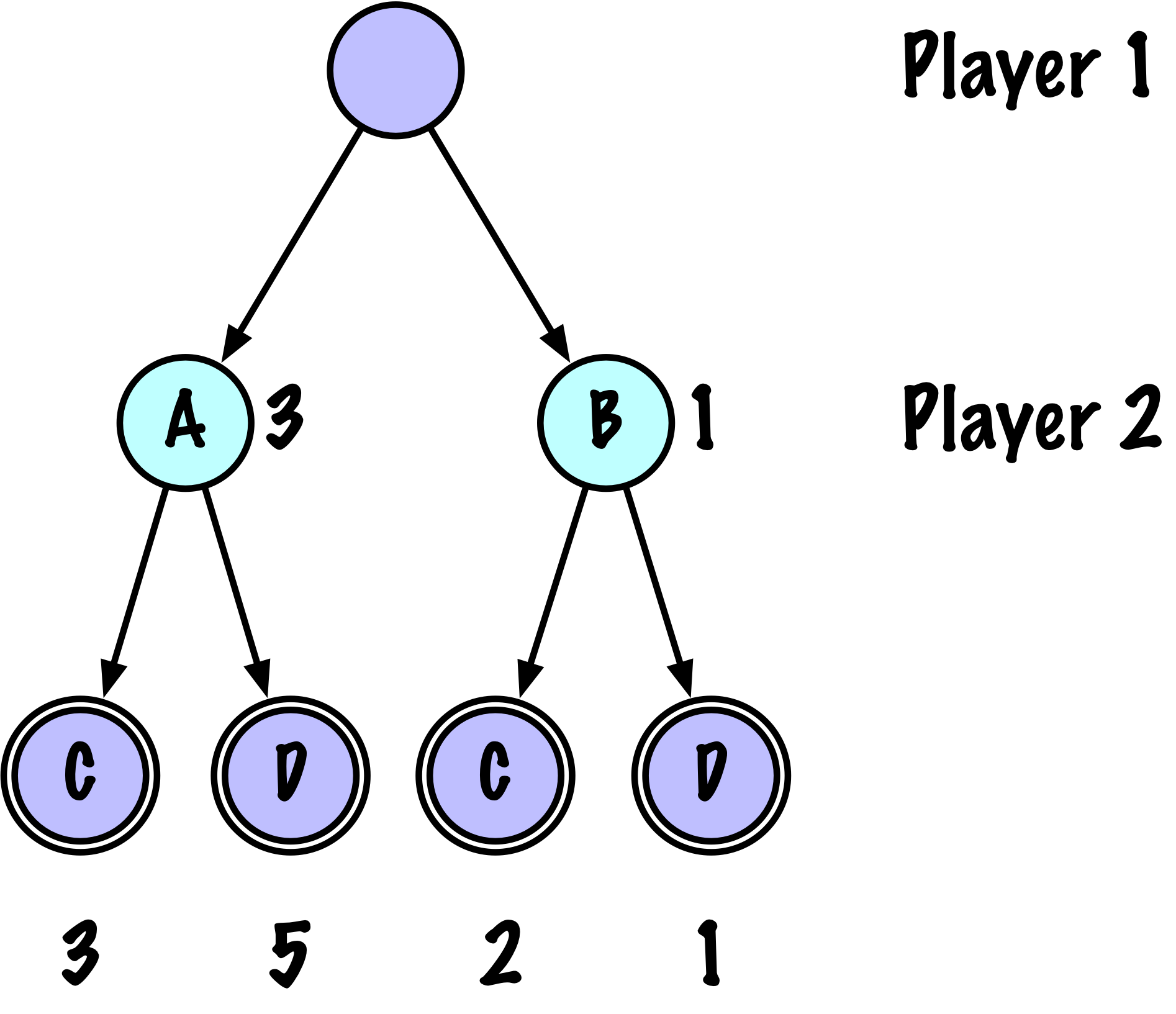
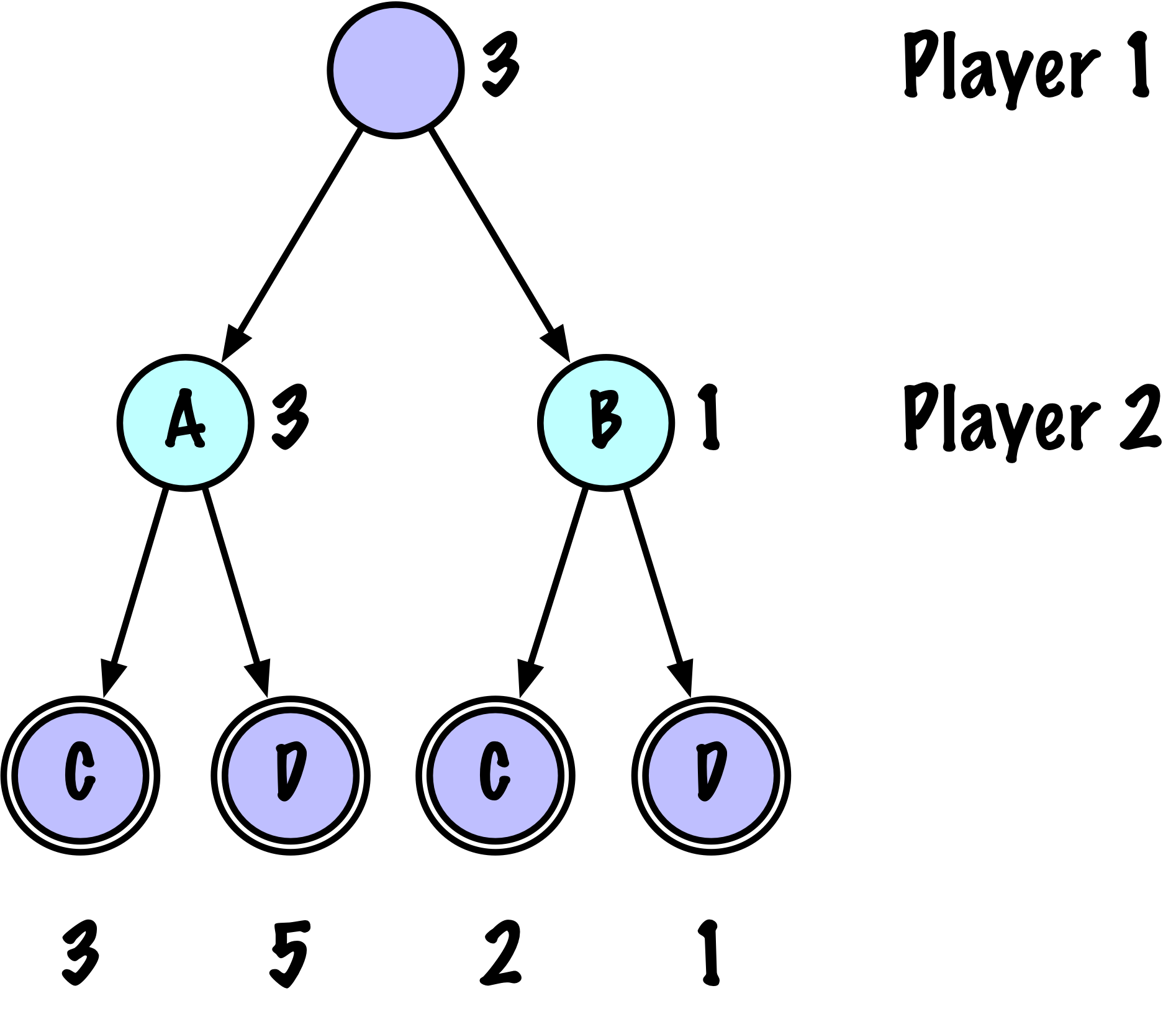
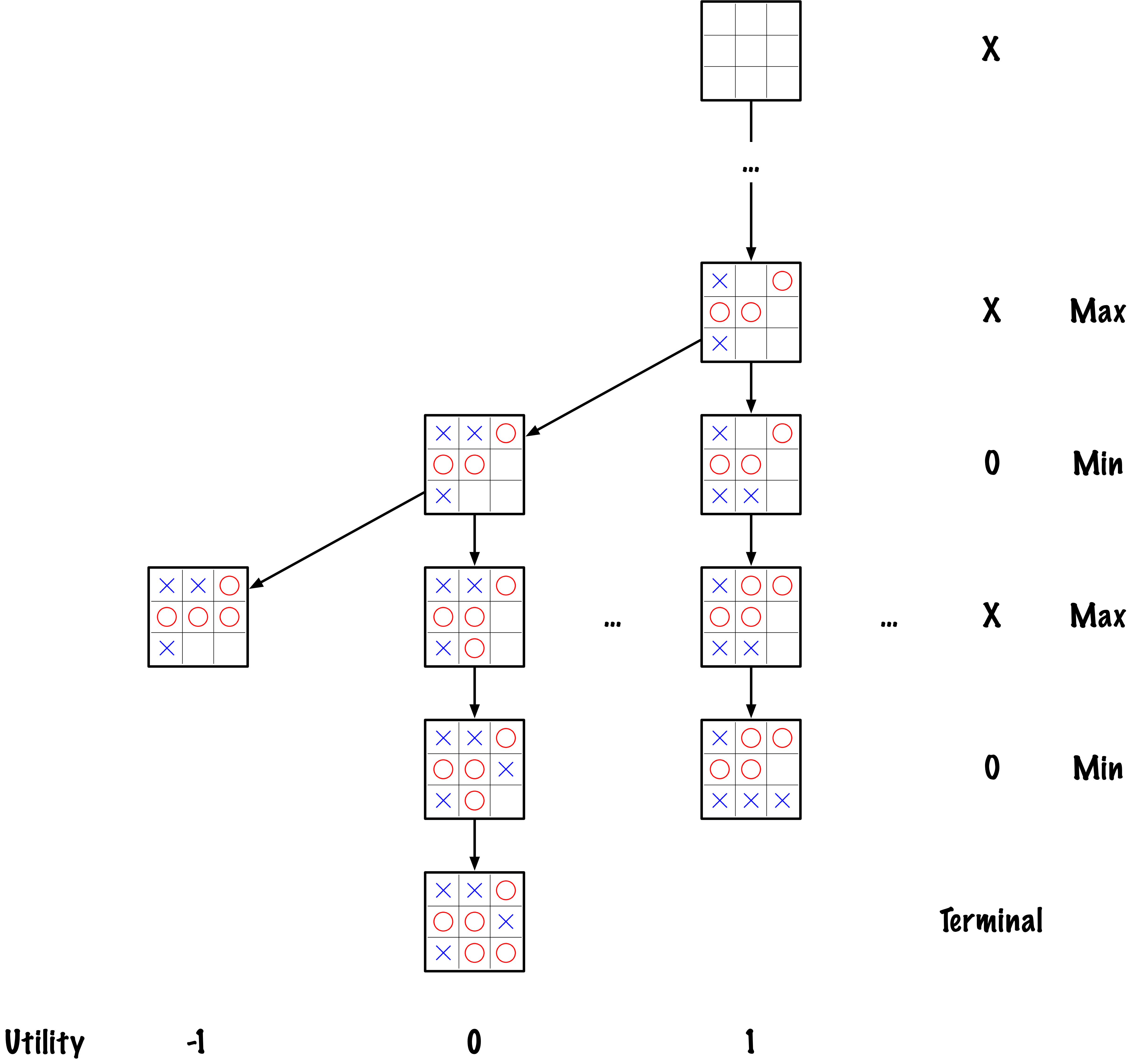
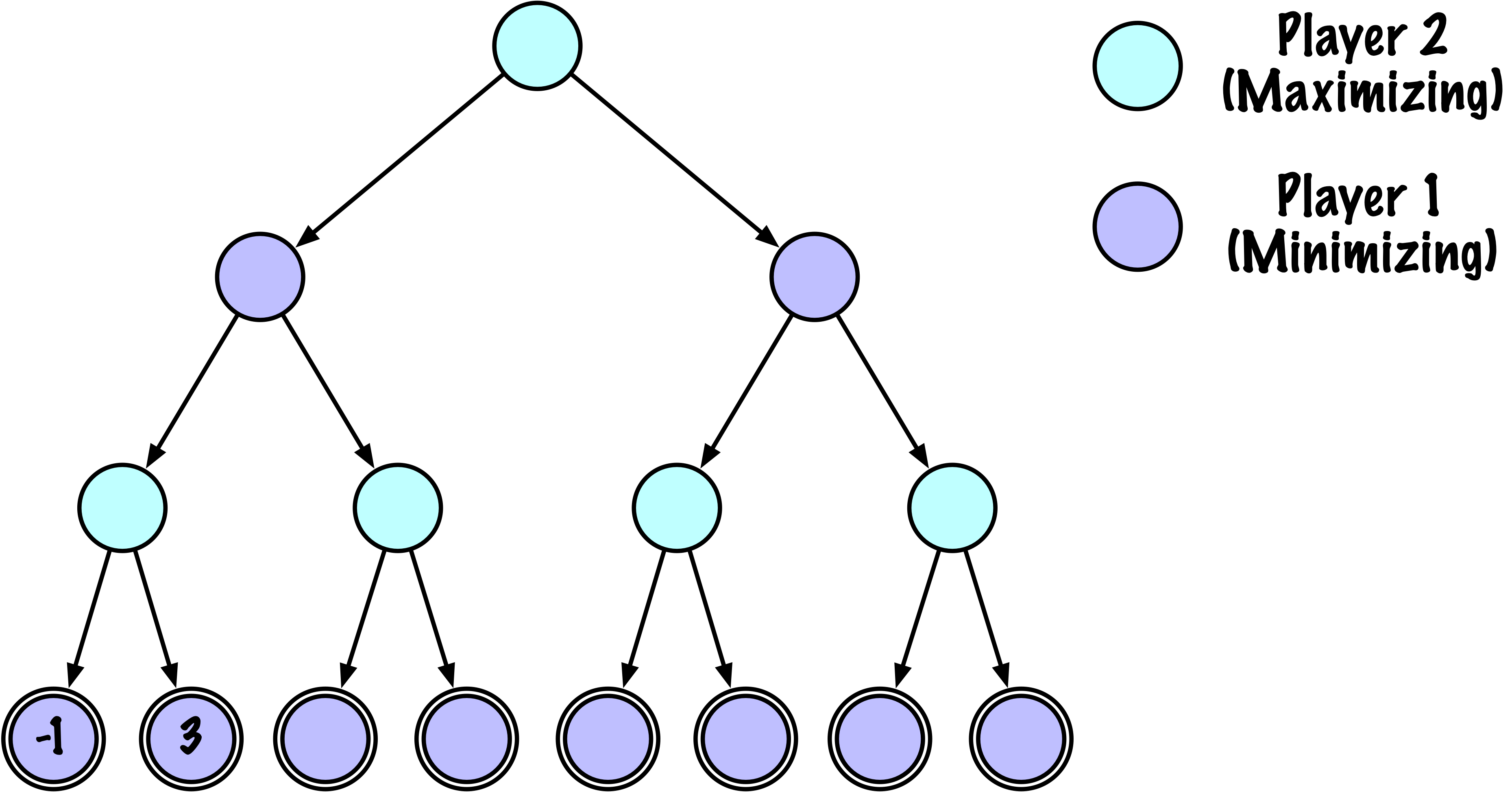
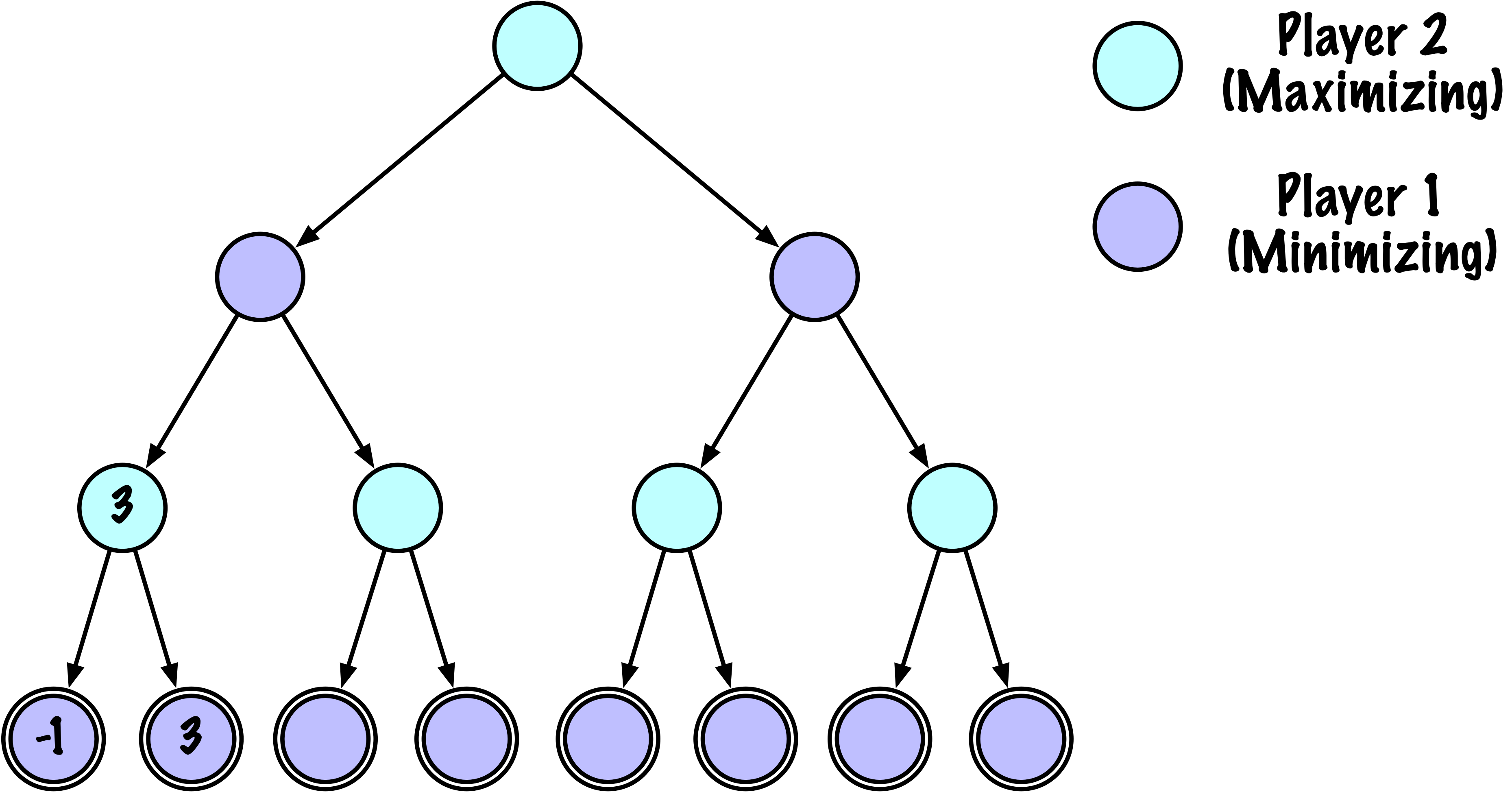
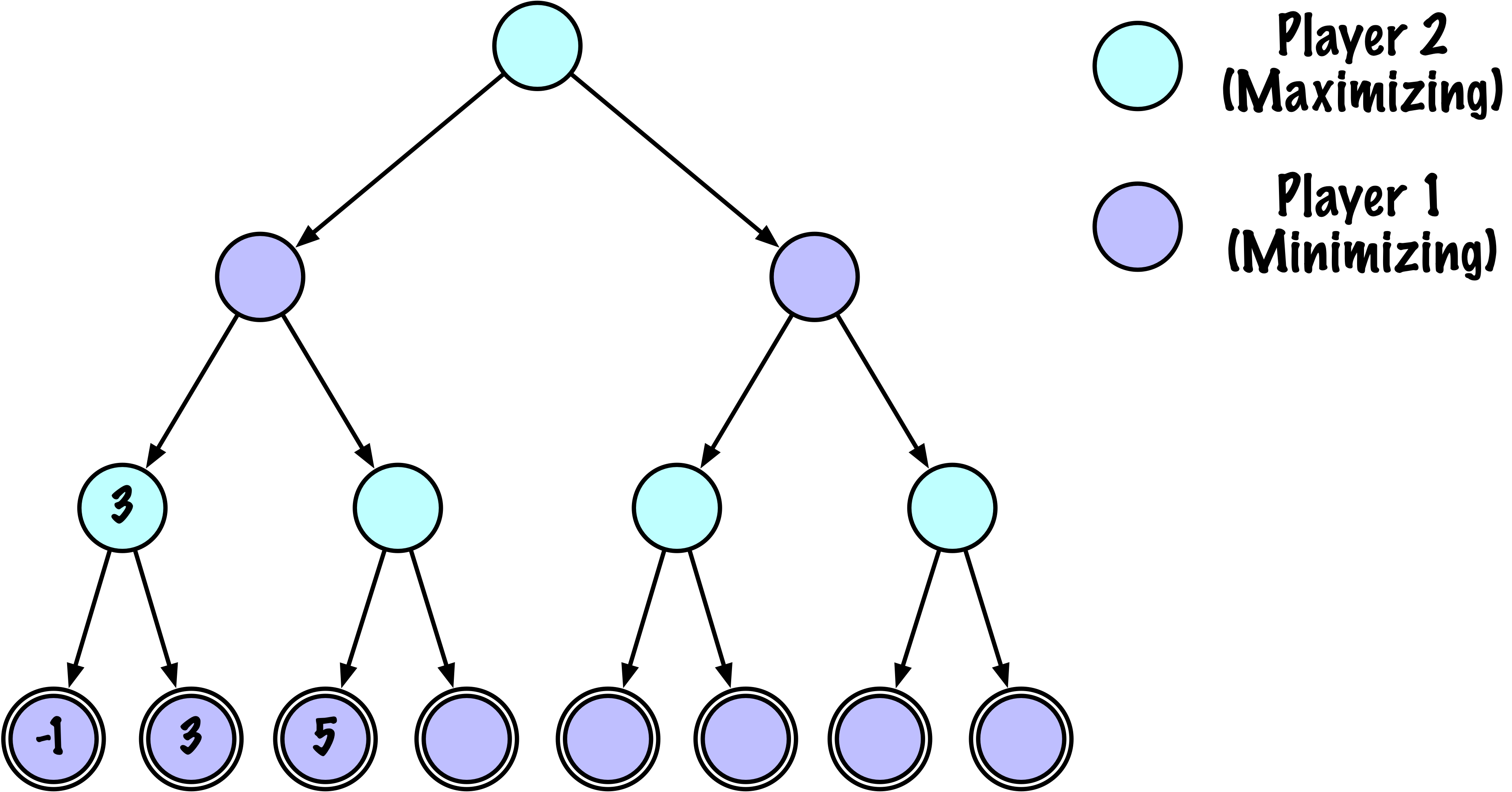
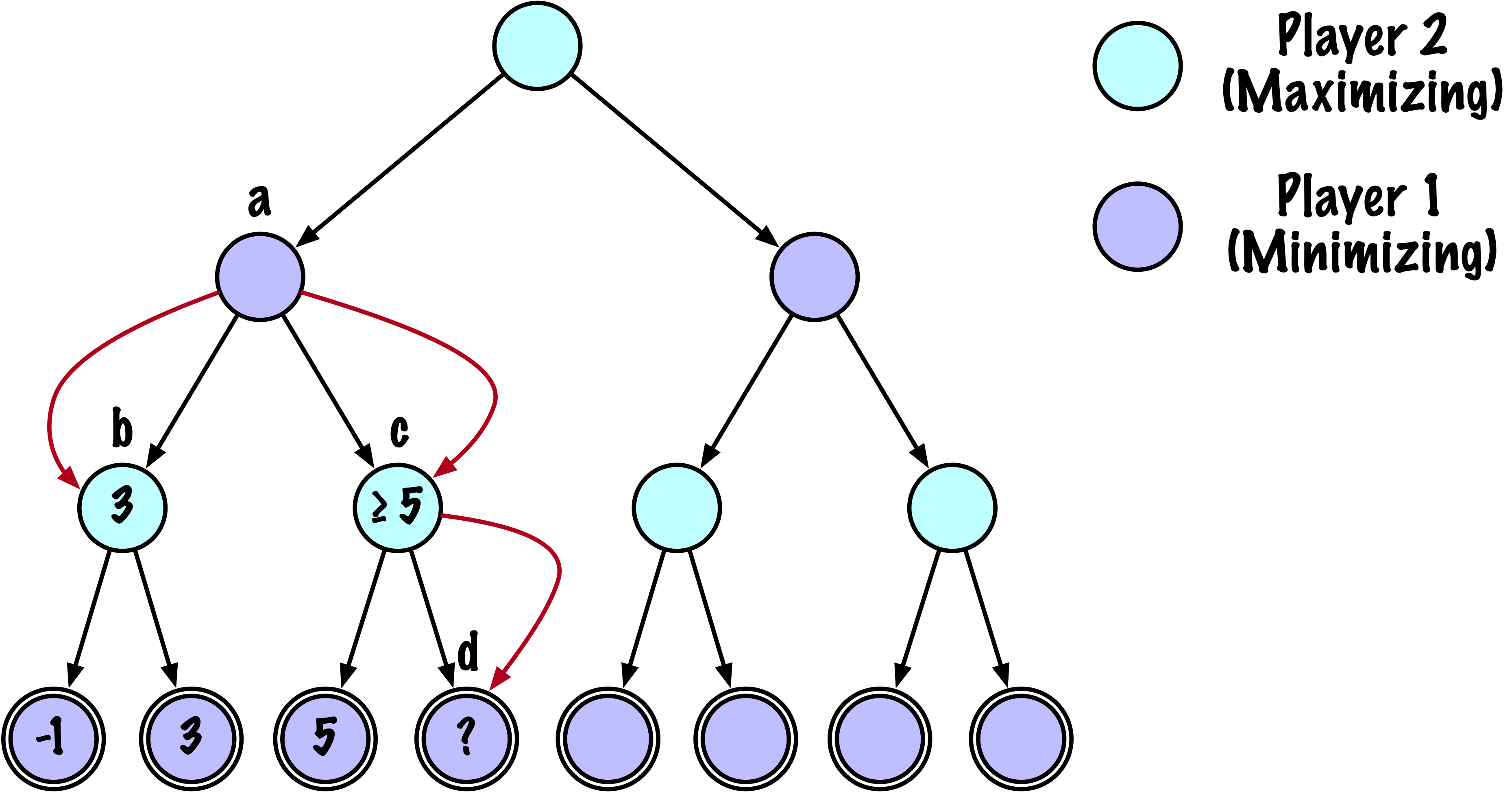
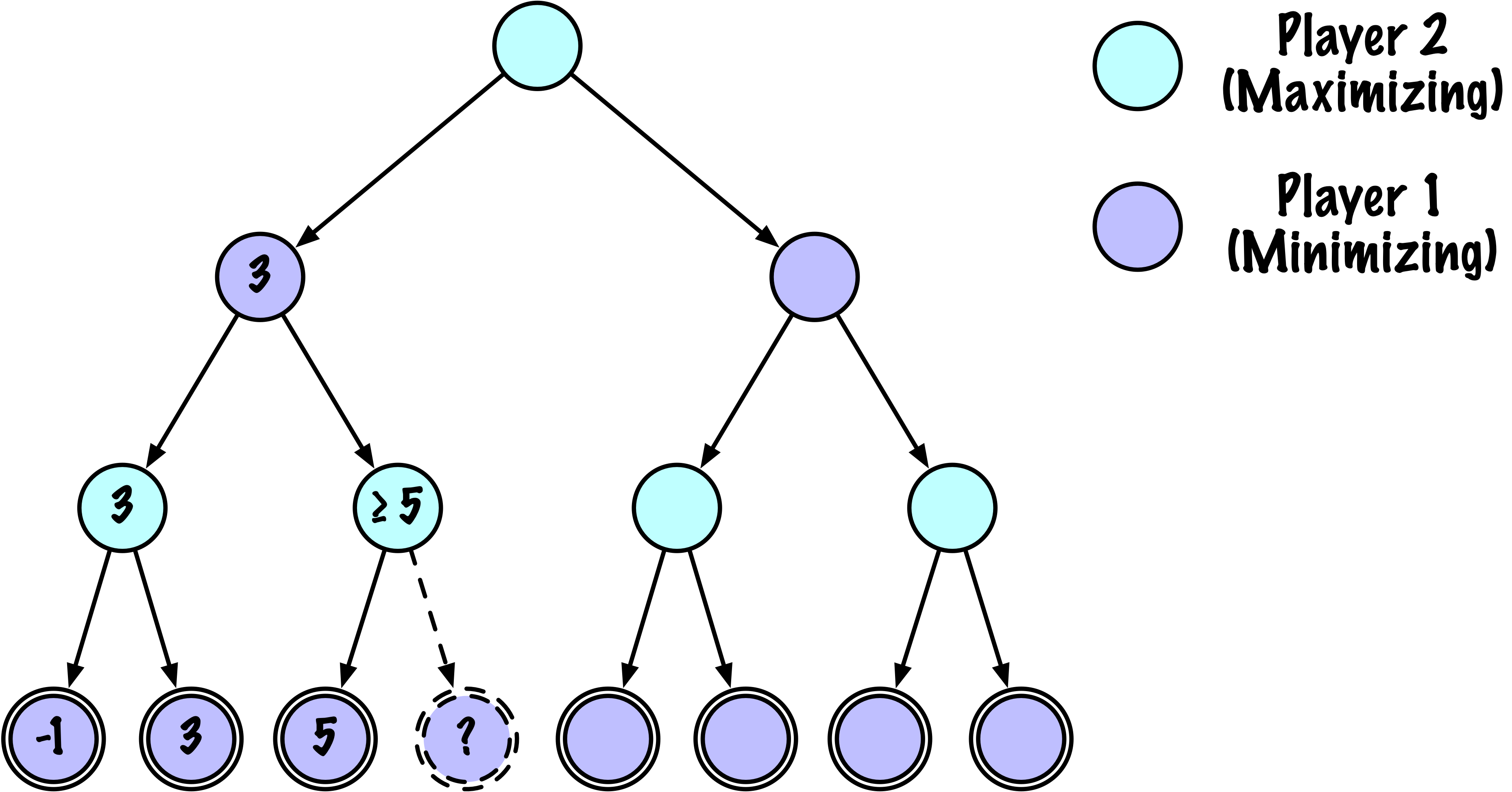
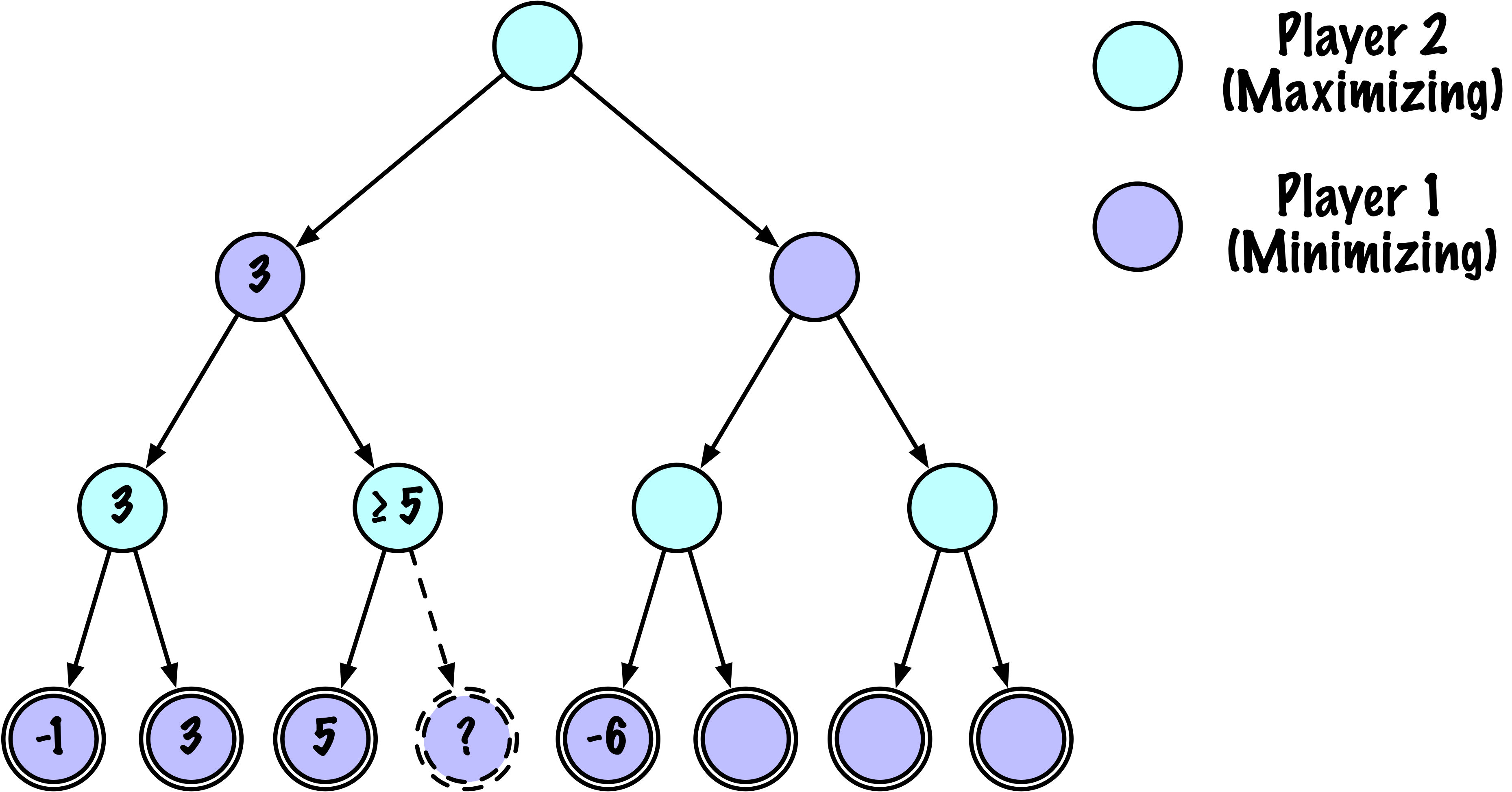
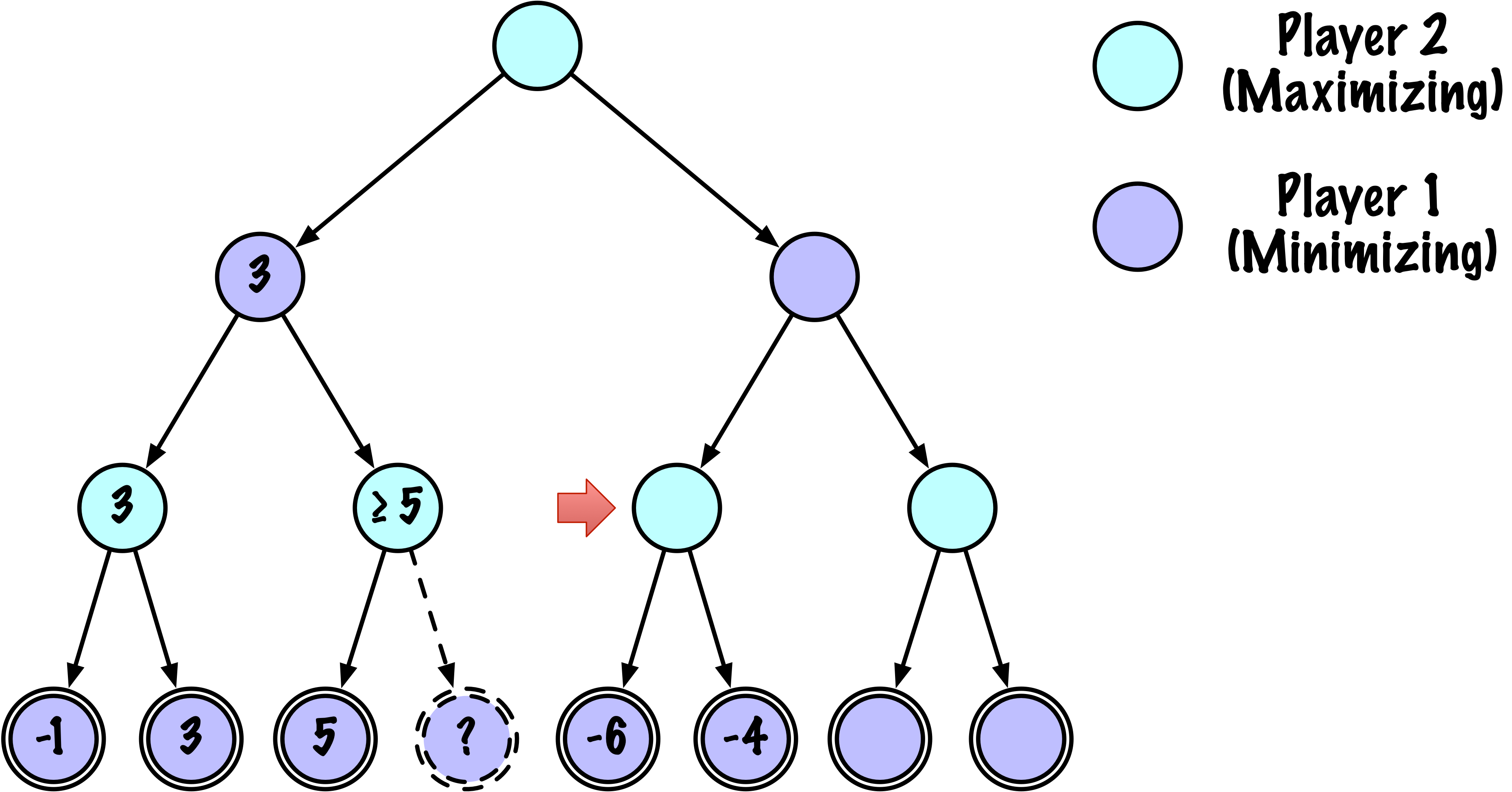
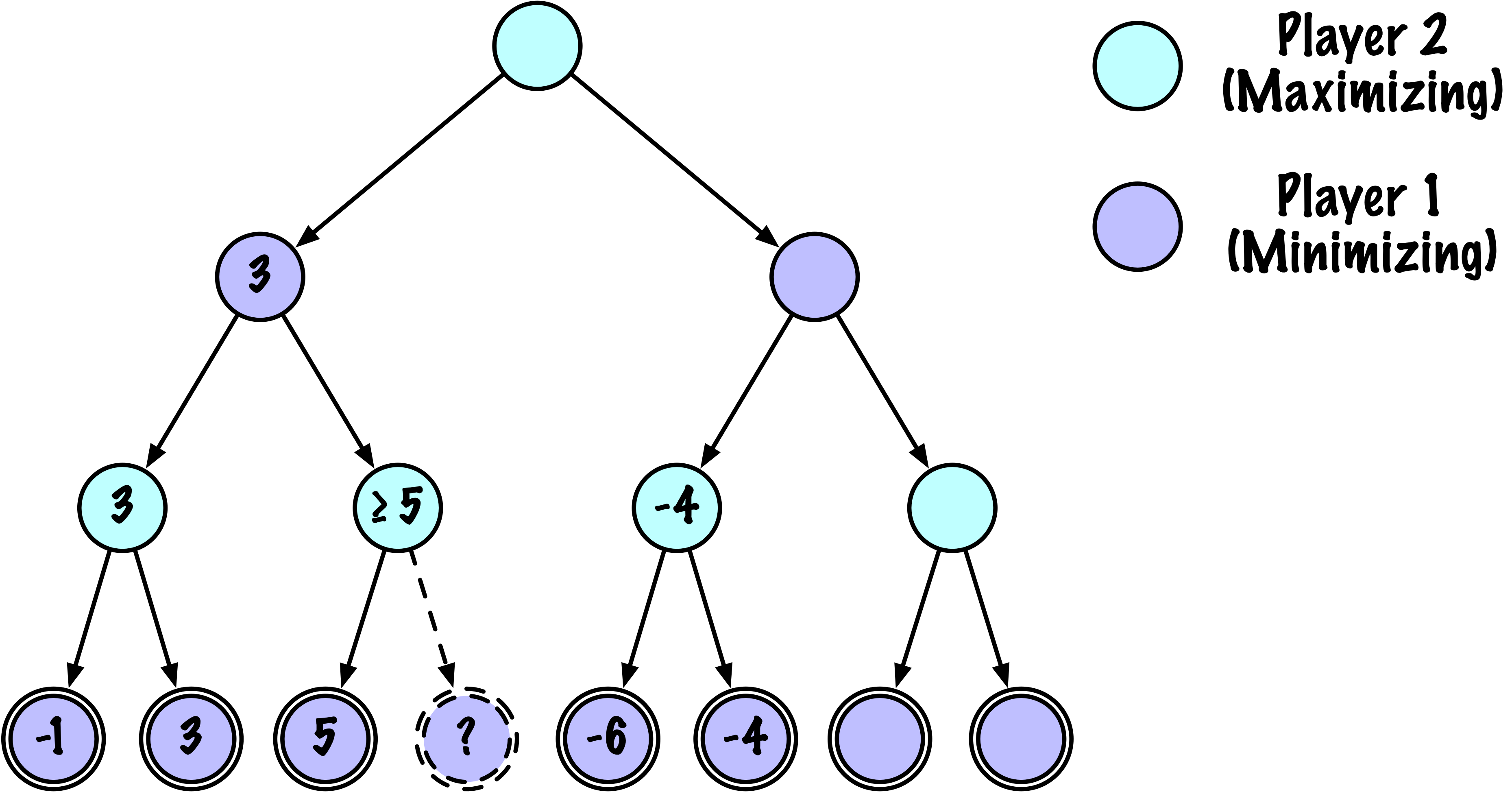
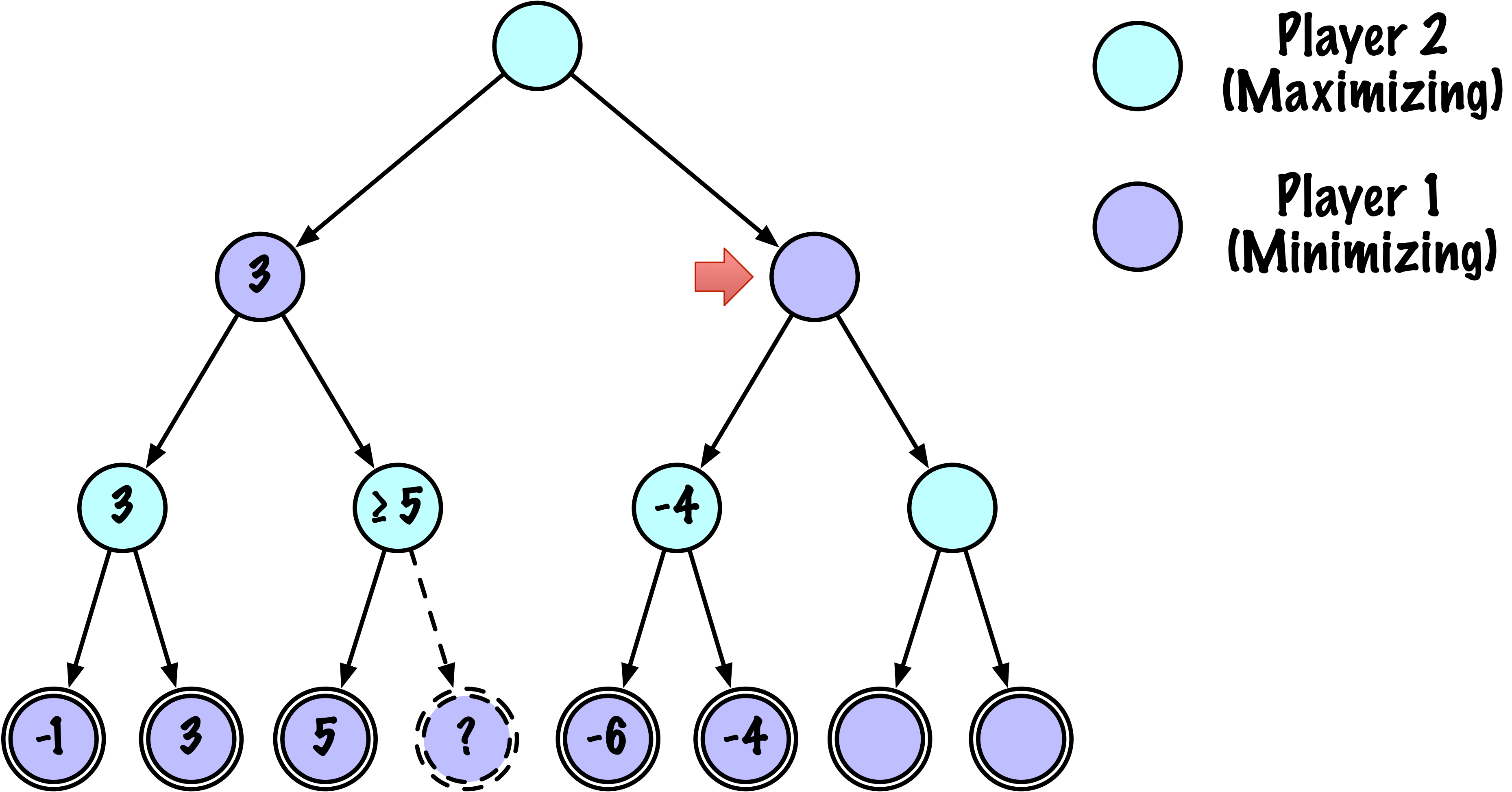
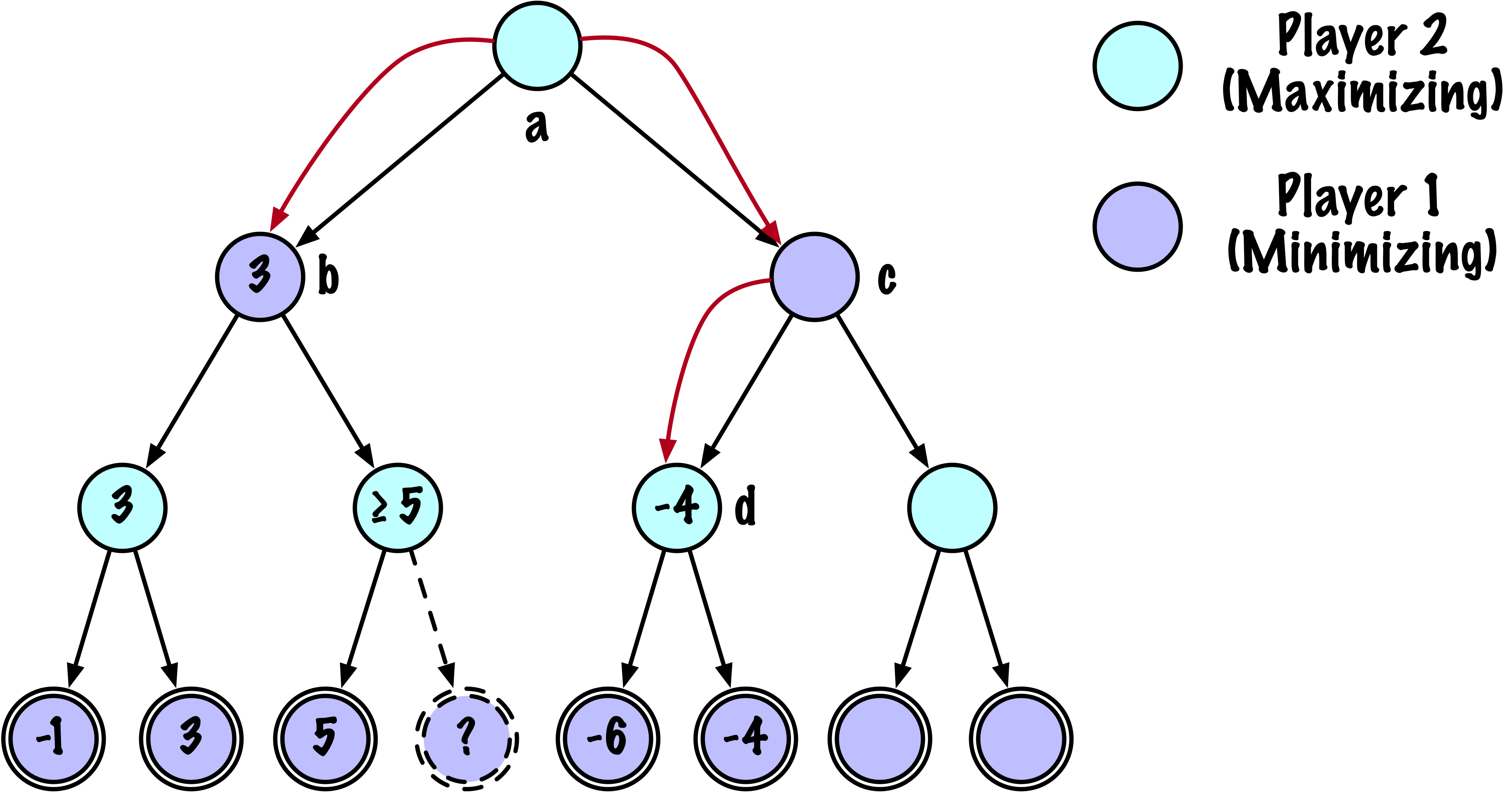
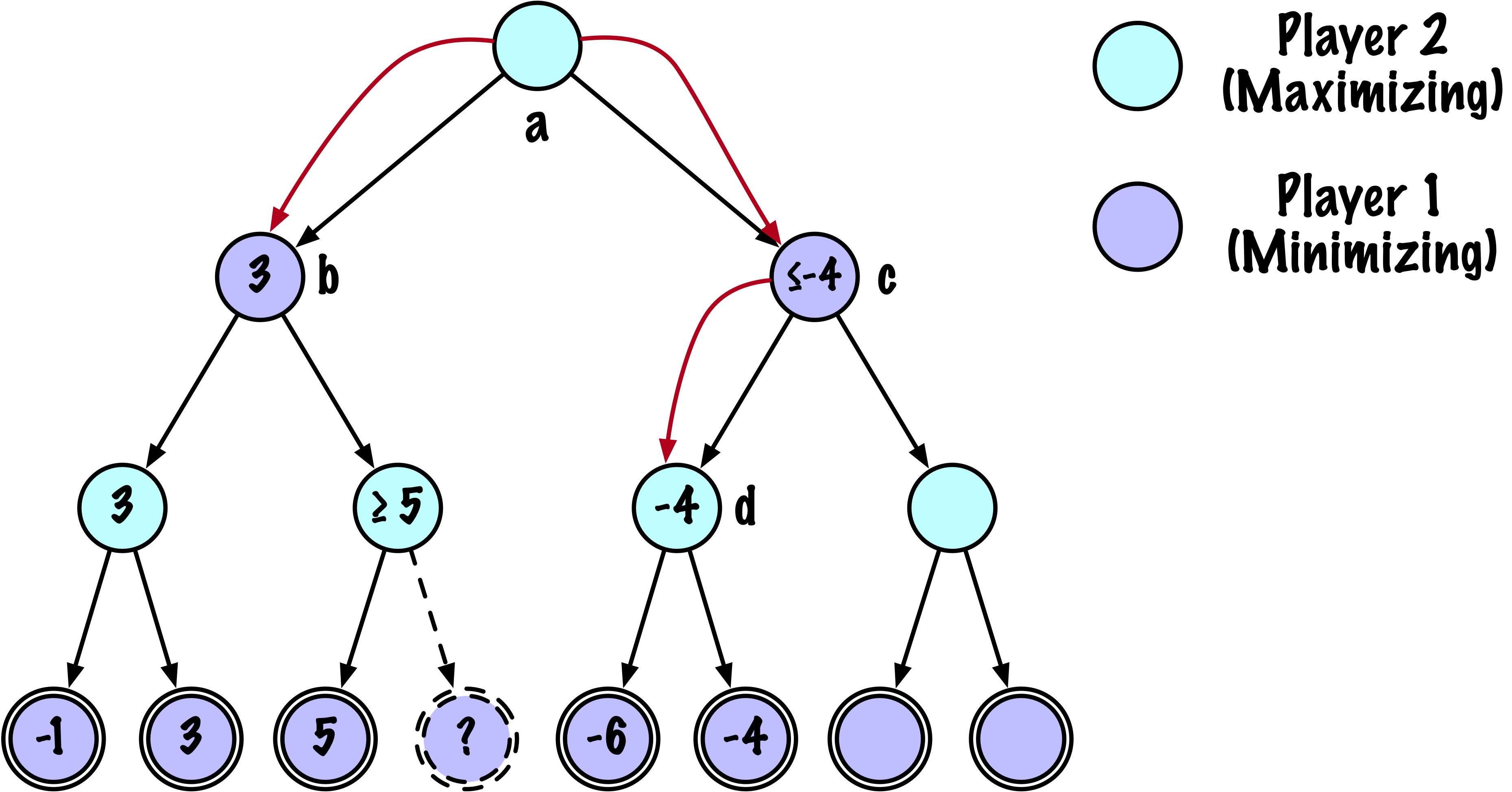
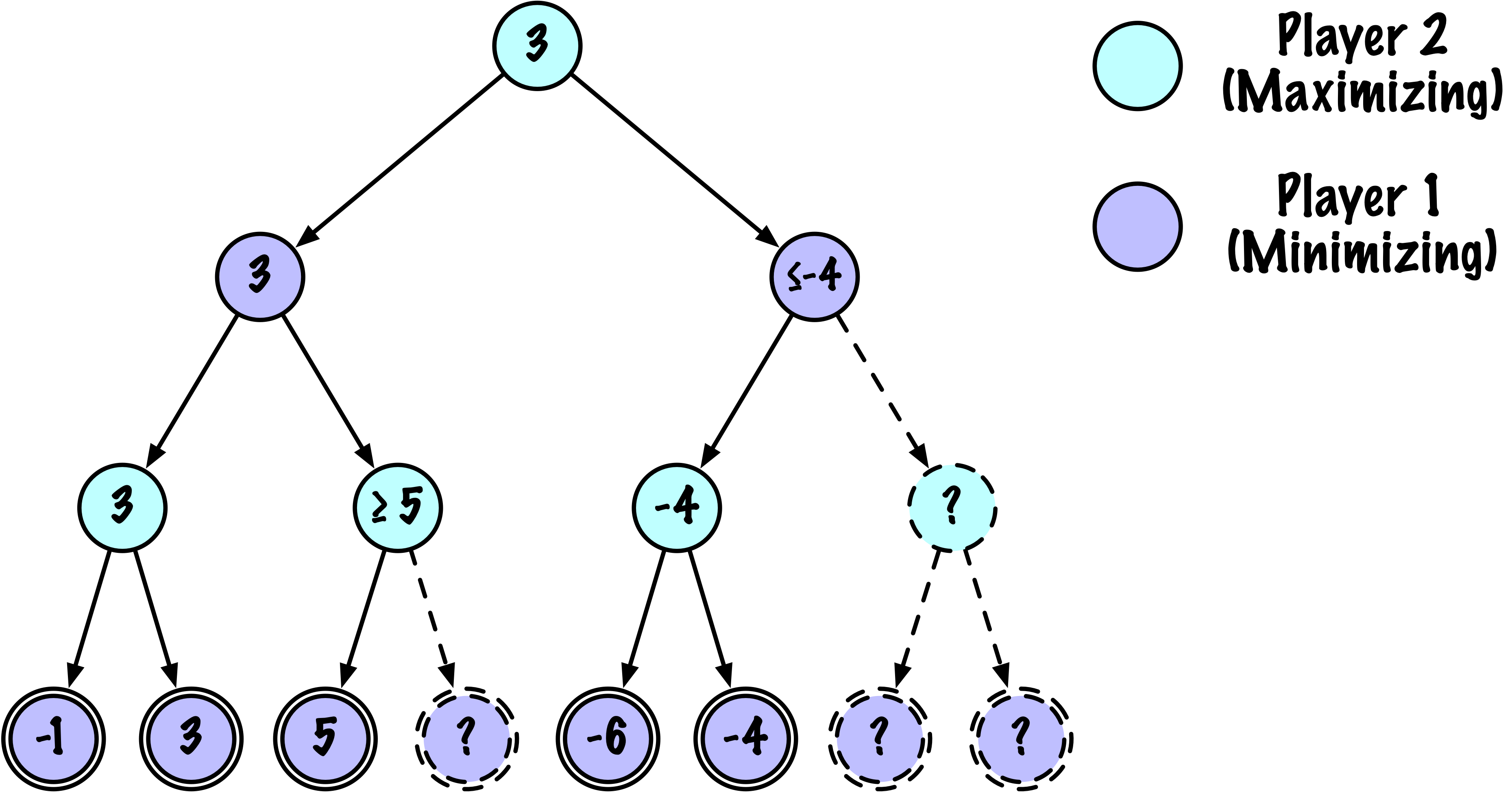
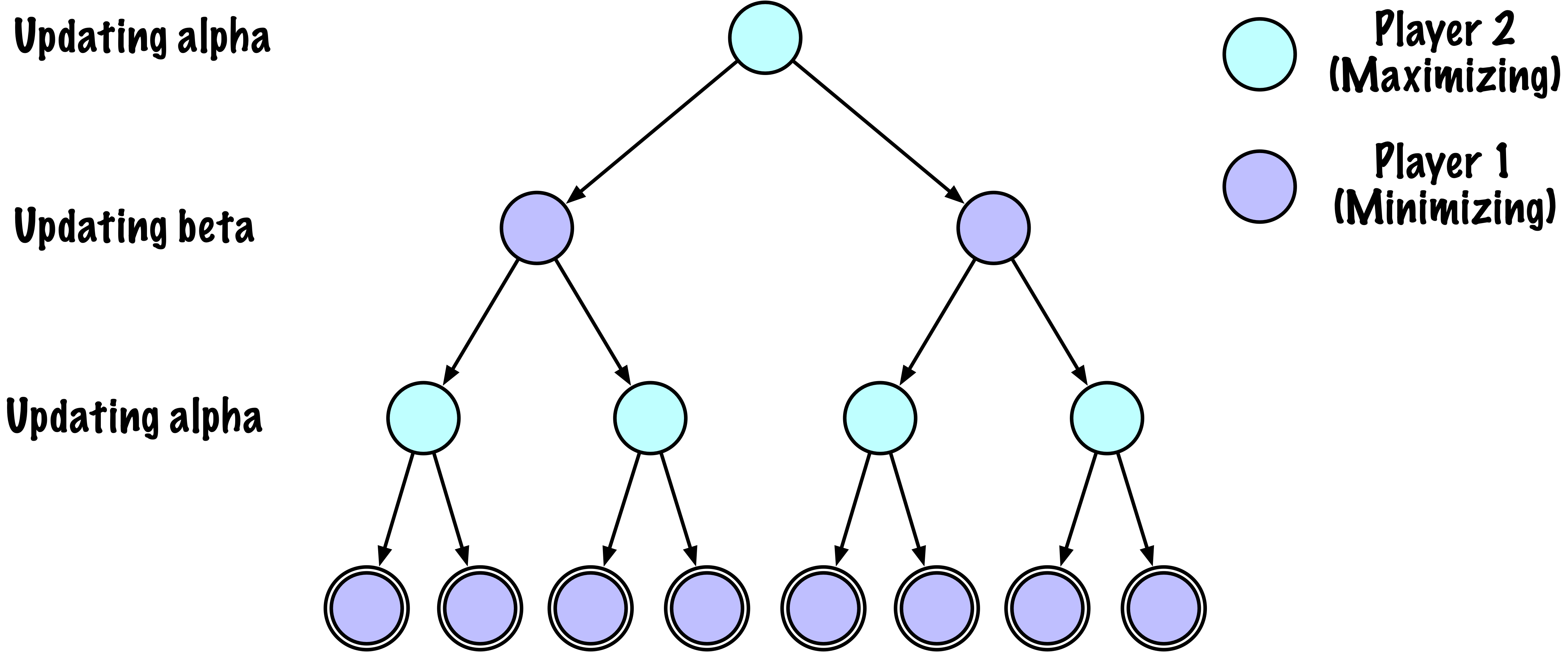
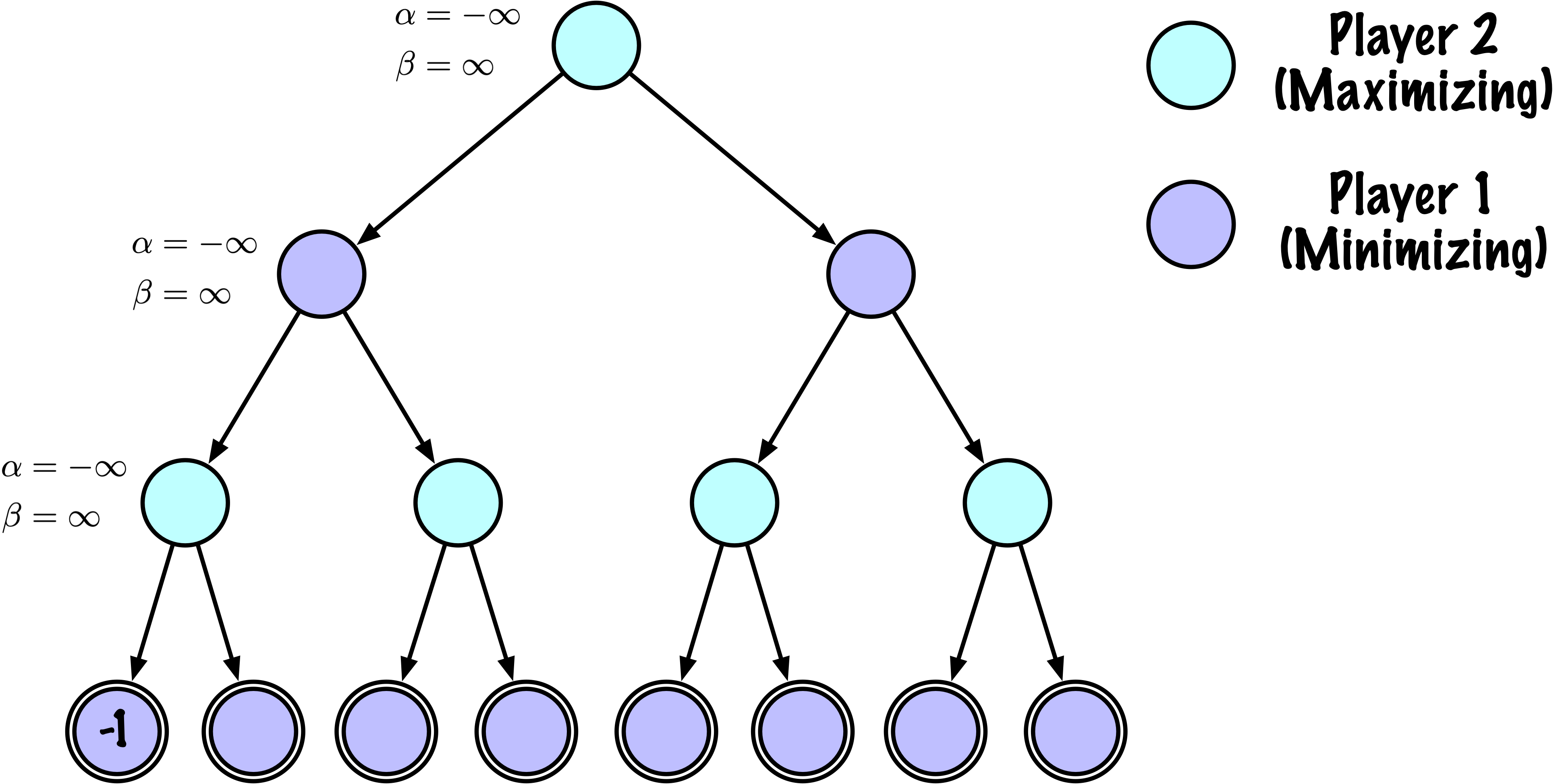
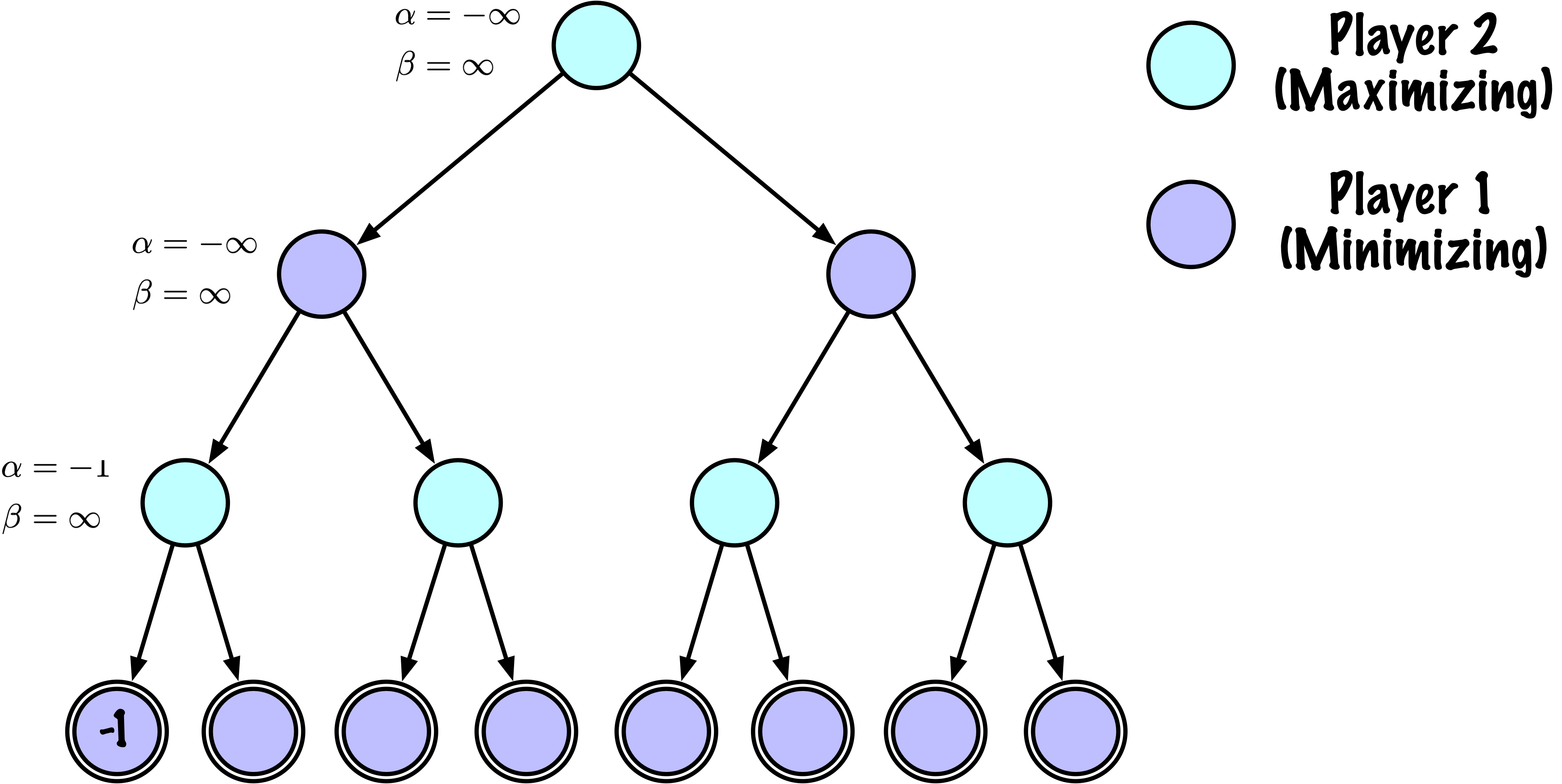
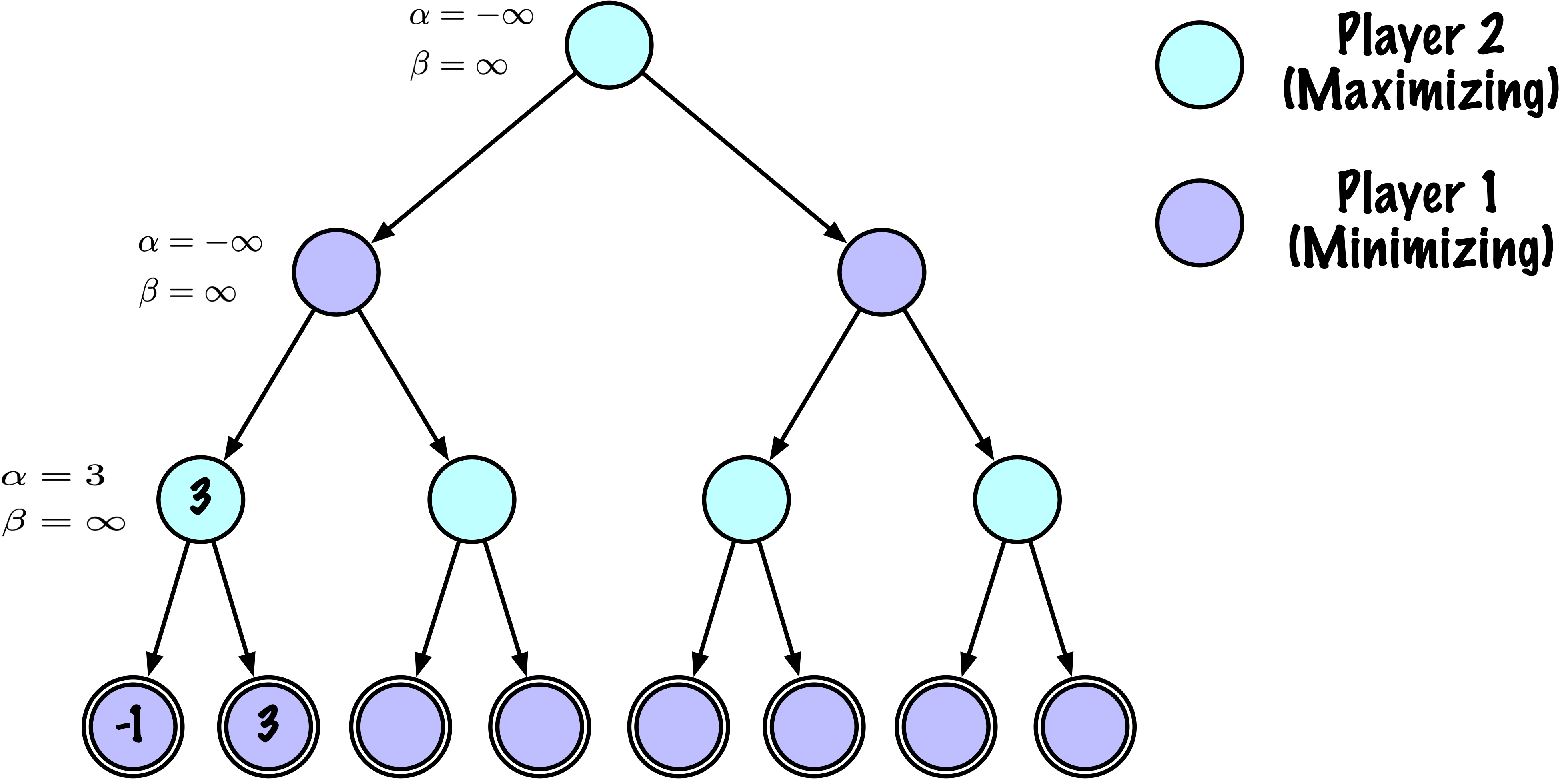
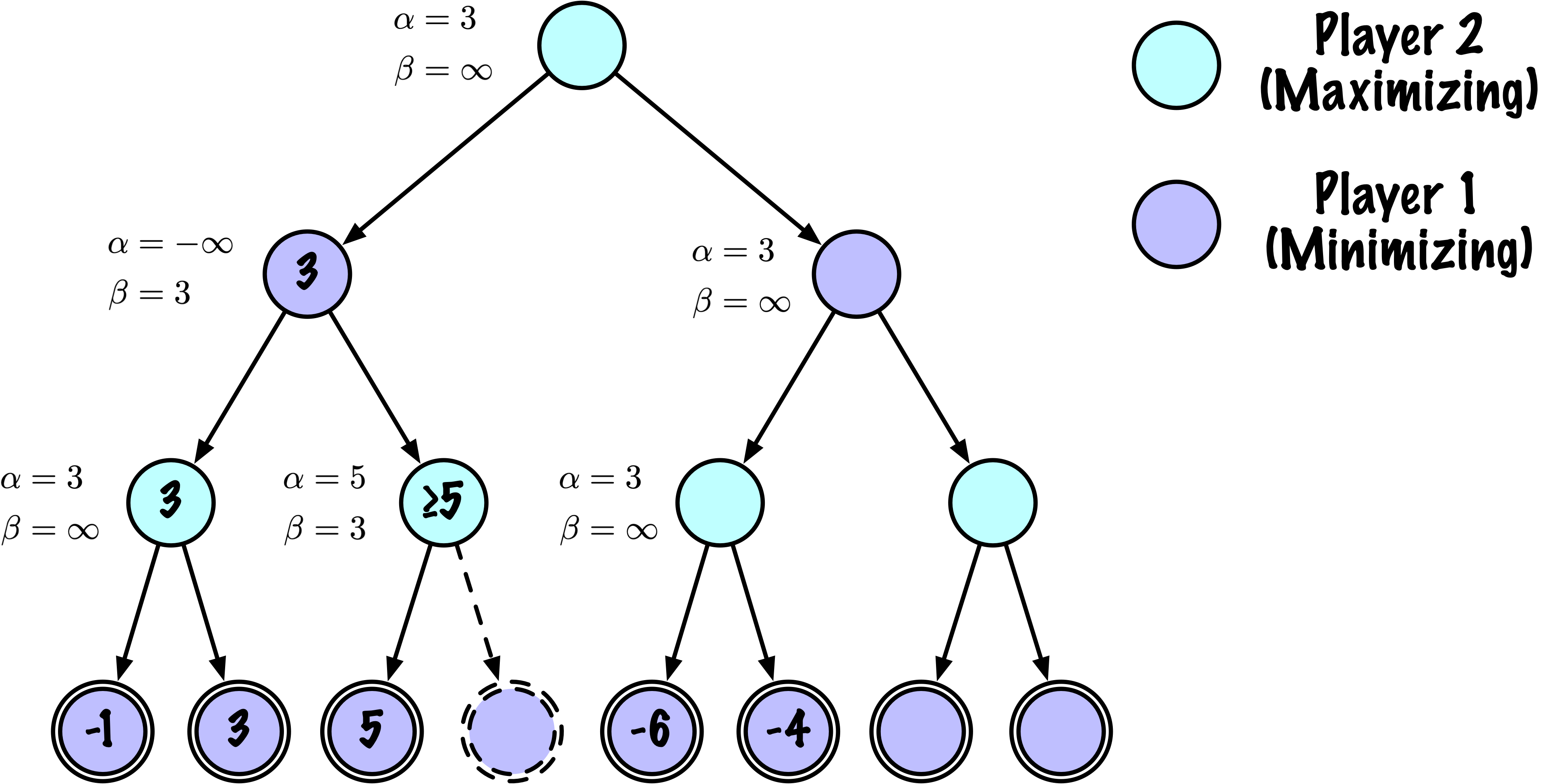
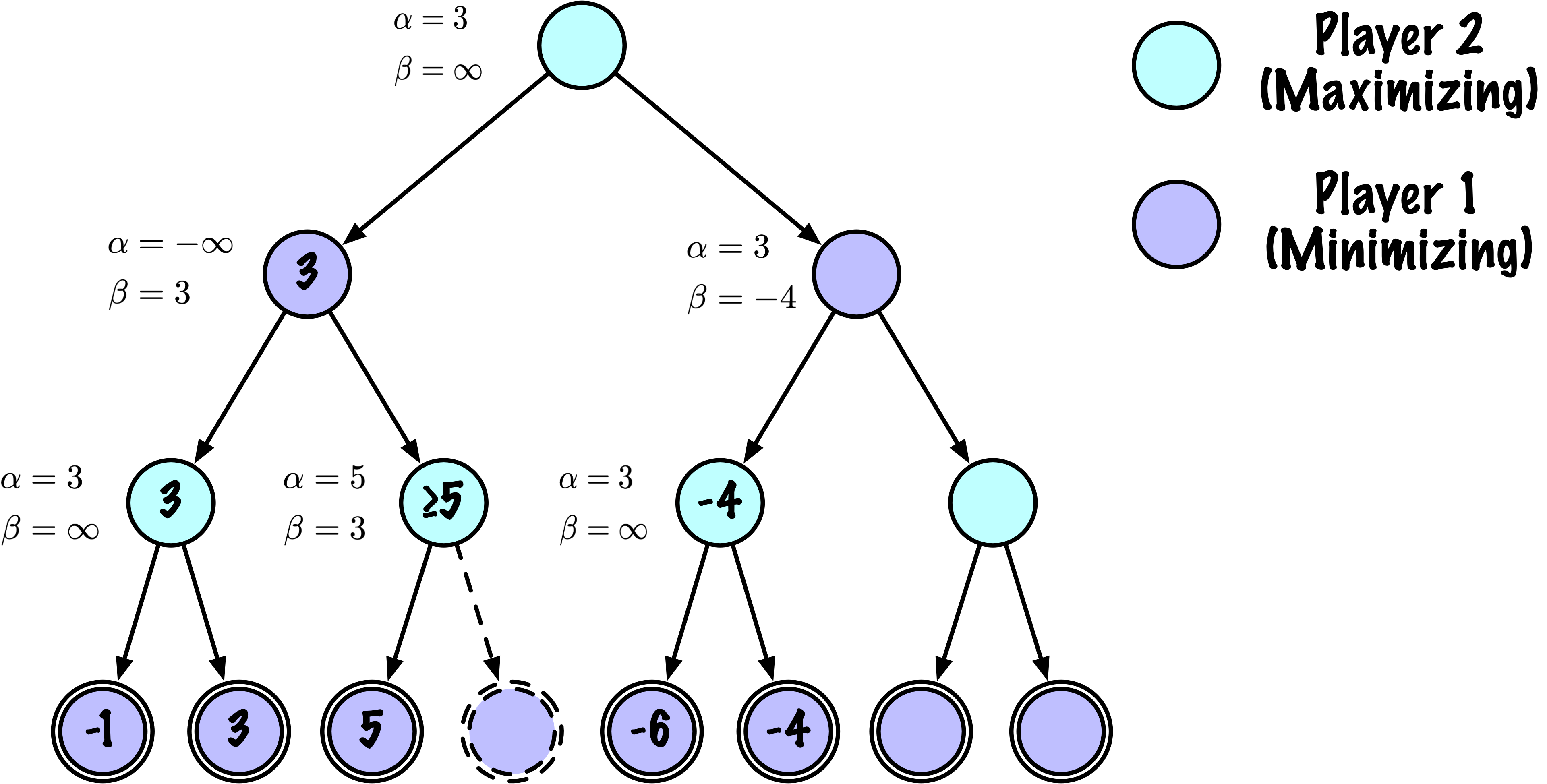
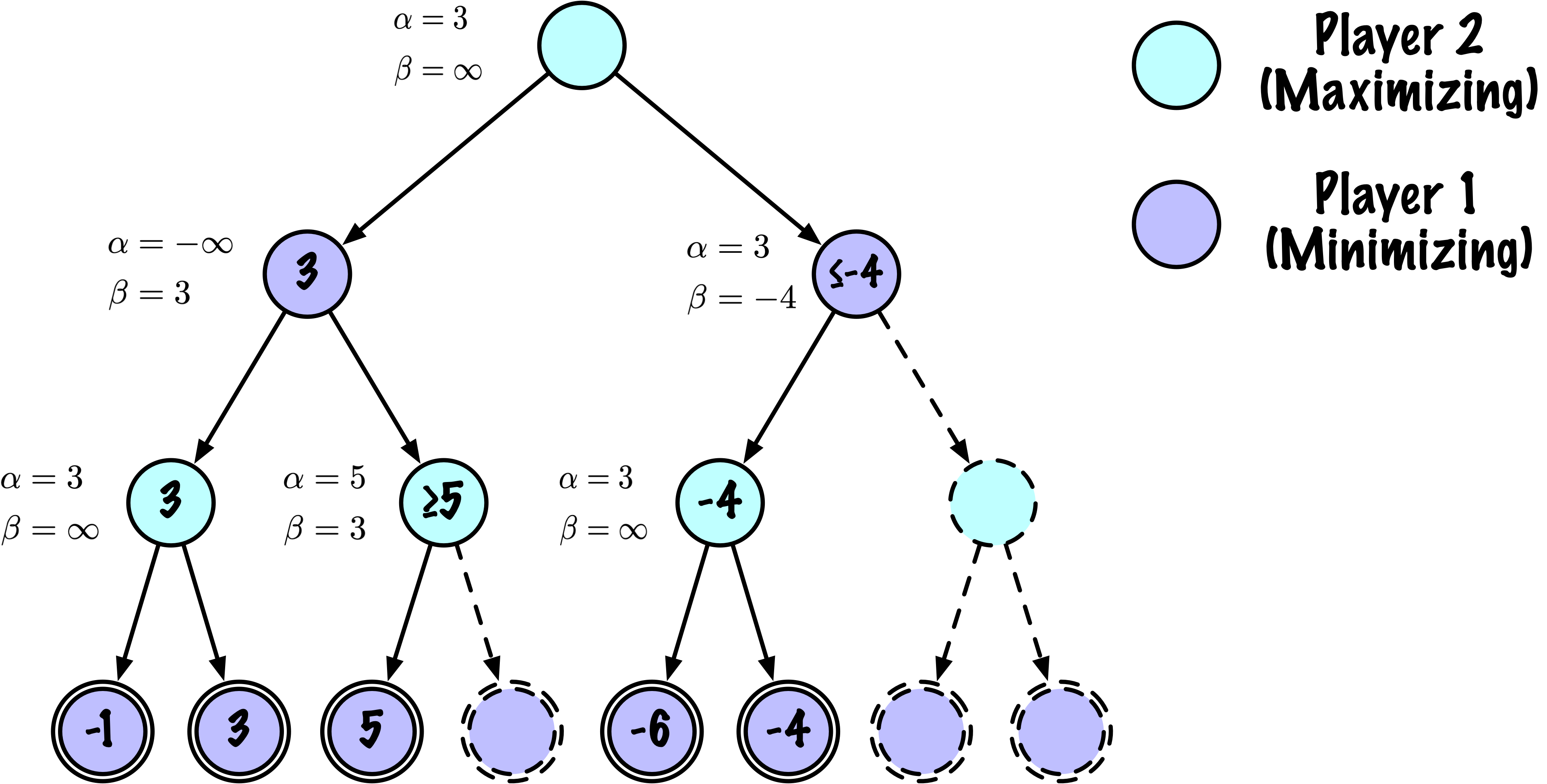
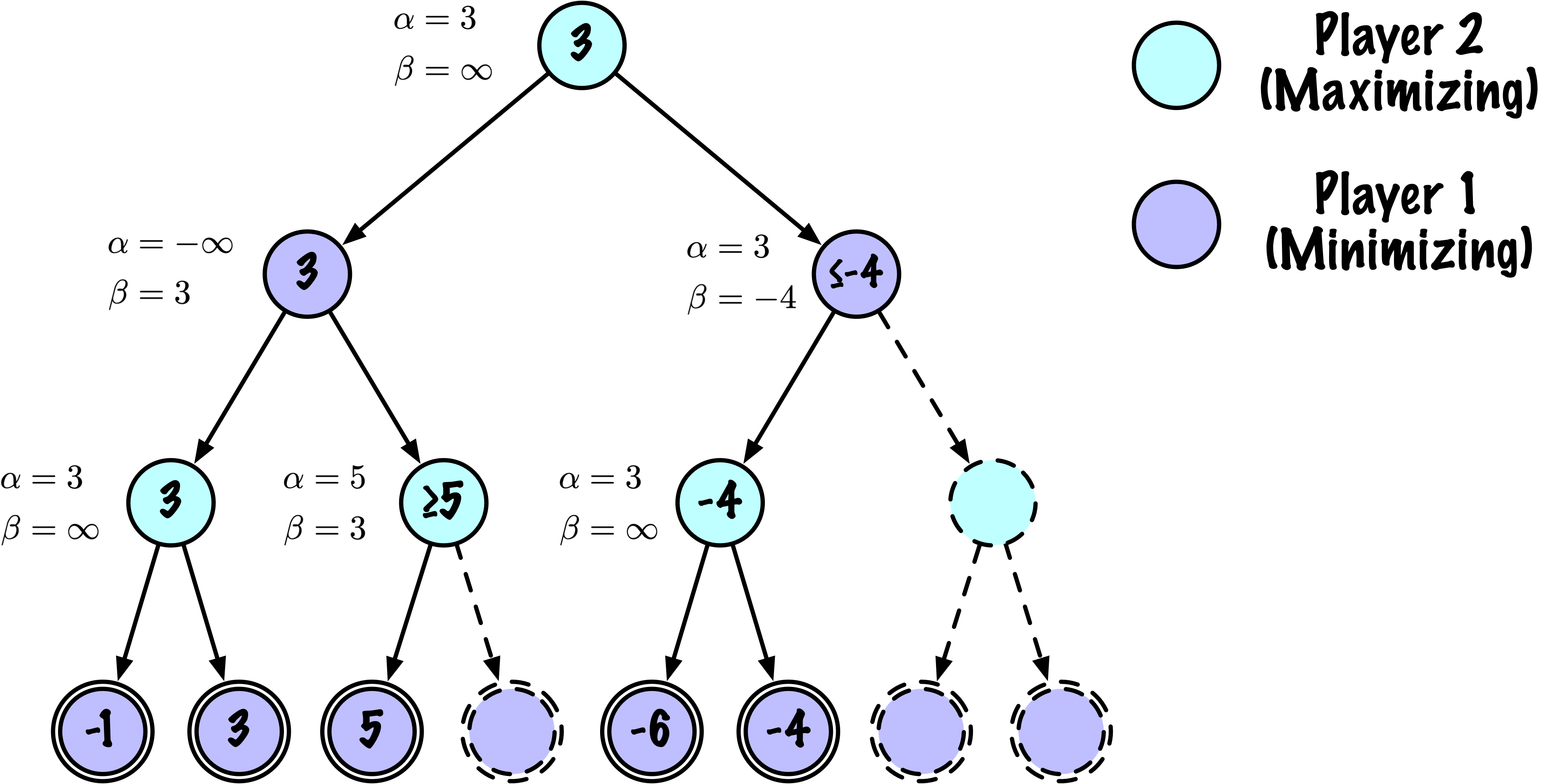
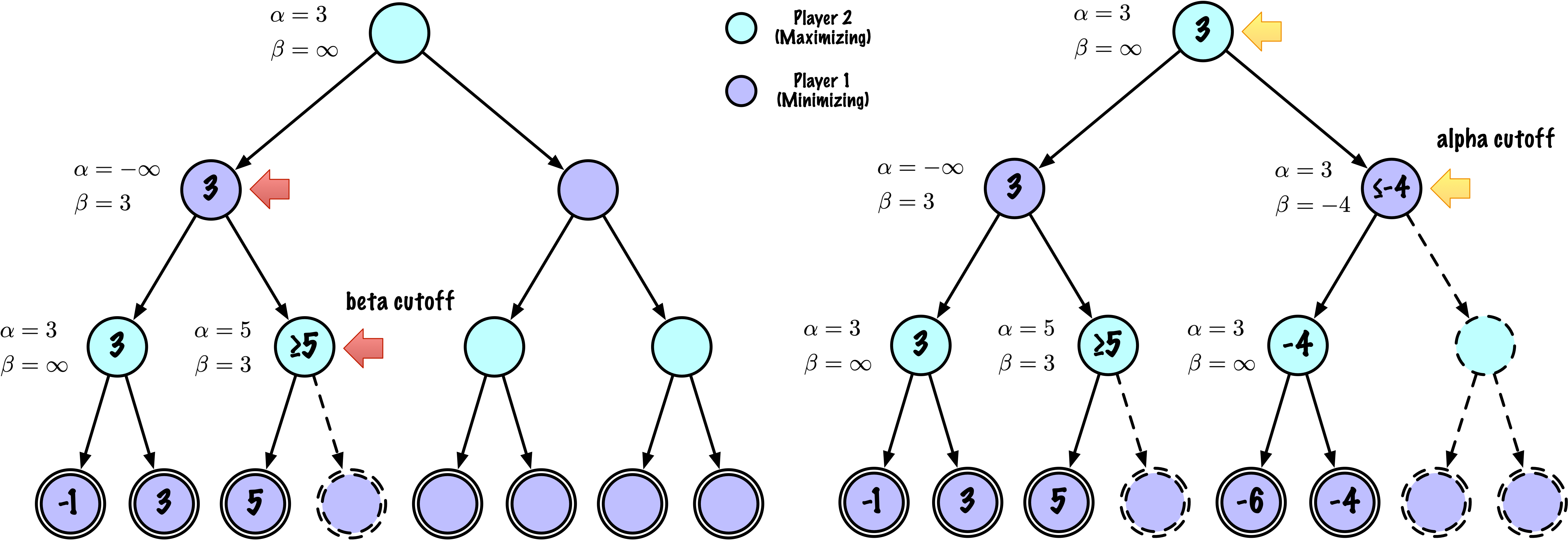
class MinimaxAlphaBetaSolverV2(Solver):
"""
A classical Minimax solver enhanced with Alpha–Beta pruning,
instrumented to count how many nodes are visited.
- Assumes "X" is the maximizing player.
- Performs a full search of the Tic–Tac–Toe game tree.
- Alpha–Beta pruning reduces the number of explored states
without changing the final result.
Instrumentation
---------------
- self.nodes_visited counts how many times _alphabeta() is called.
"""
def __init__(self):
# Count how many nodes have been visited in the current run
self.nodes_visited = 0
# ------------------------------------------------------------
# Solver interface
# ------------------------------------------------------------
def select_move(self, game, state, player):
"""
Choose the best move for `player` using Minimax with
Alpha–Beta pruning.
For Tic–Tac–Toe, depth=9 suffices to search the entire game.
"""
self.game = game
maximizing = (player == "X")
value, move = self._alphabeta(
state=state,
player=player,
maximizing=maximizing,
depth=9,
alpha=-math.inf,
beta=math.inf
)
return move
def reset(self):
"""
Reset any per-game state.
Called by GameRunner (or similar) at the start of a new game.
"""
self.nodes_visited = 0
# ------------------------------------------------------------
# Private
# ------------------------------------------------------------
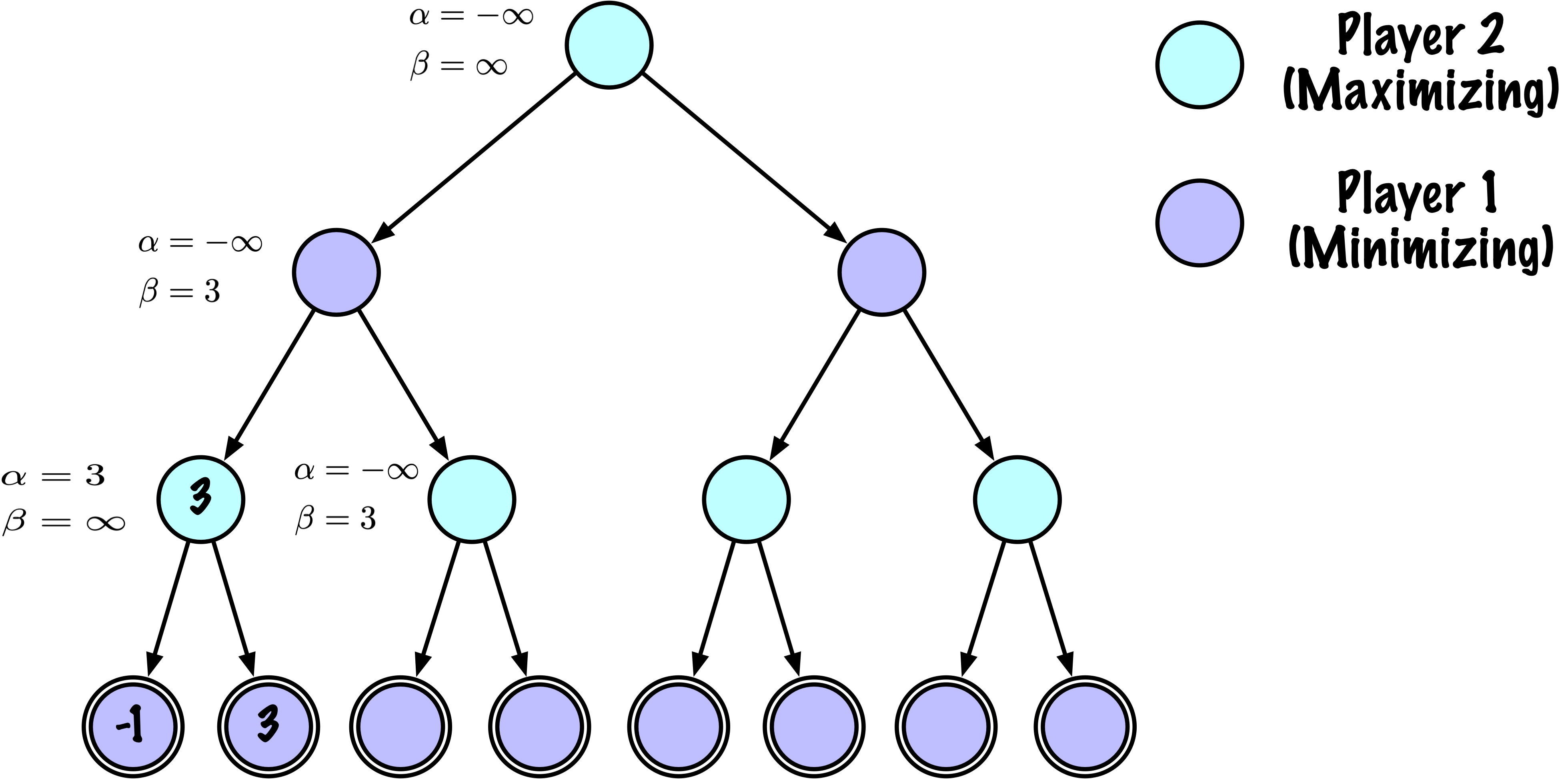
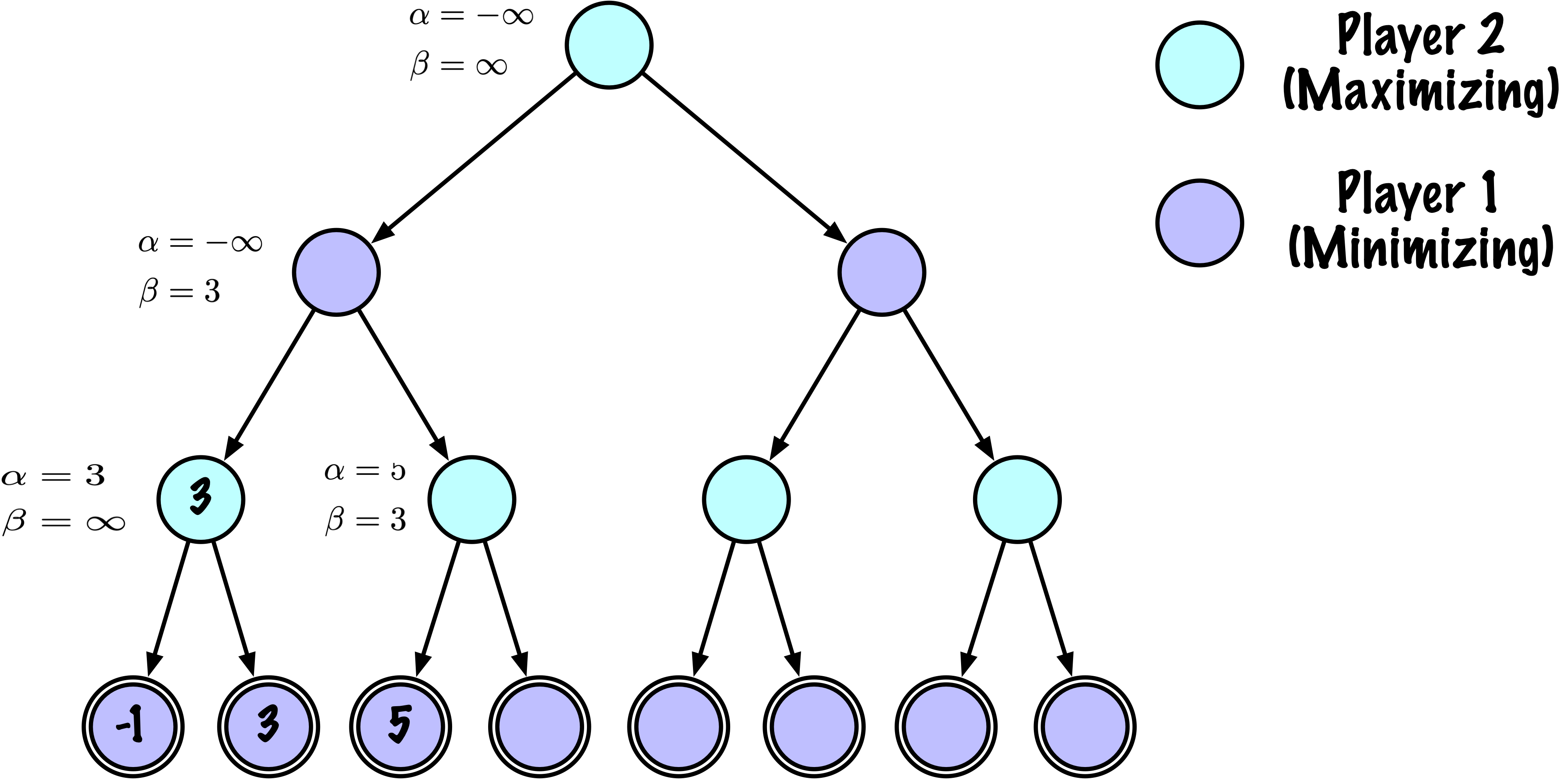
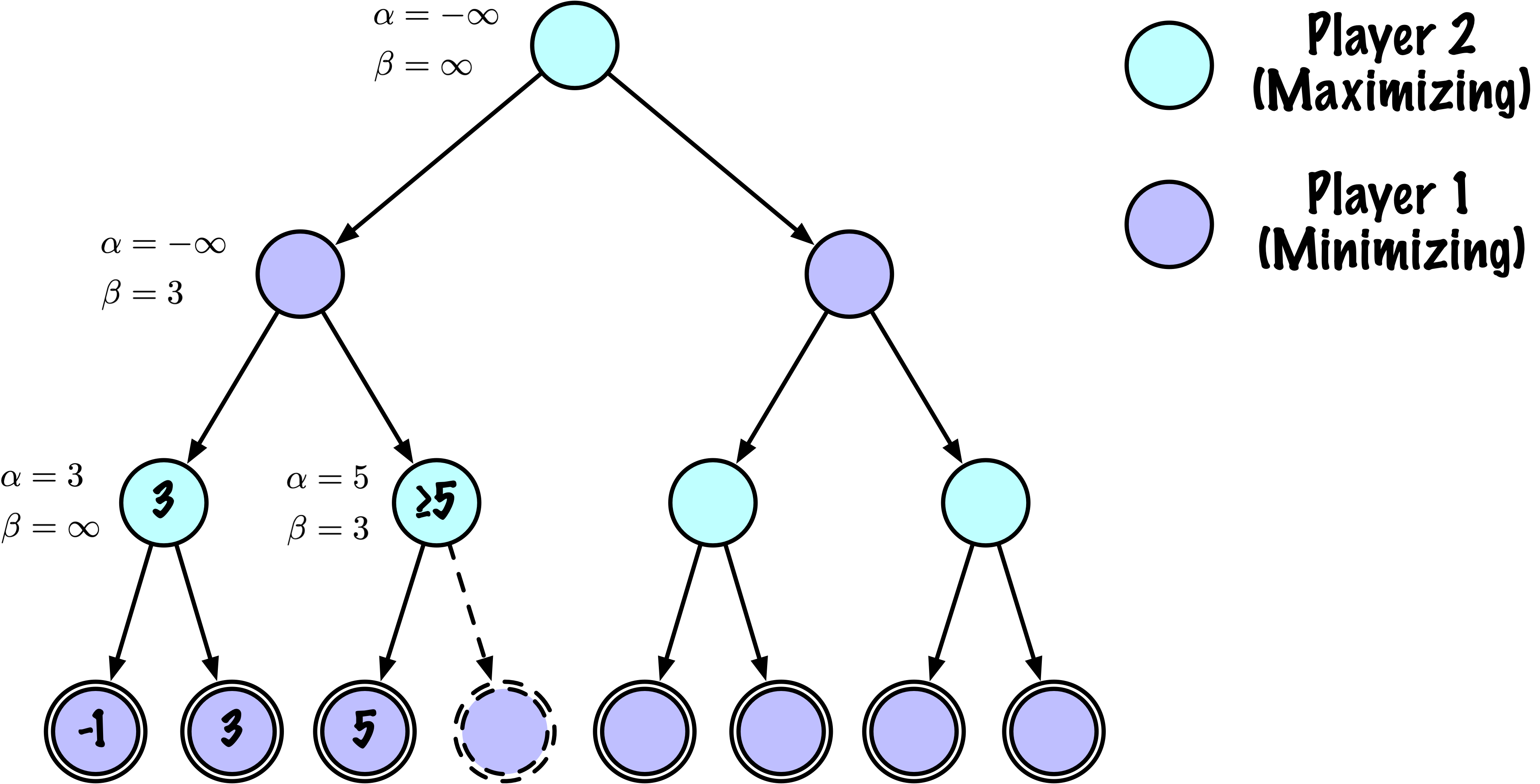
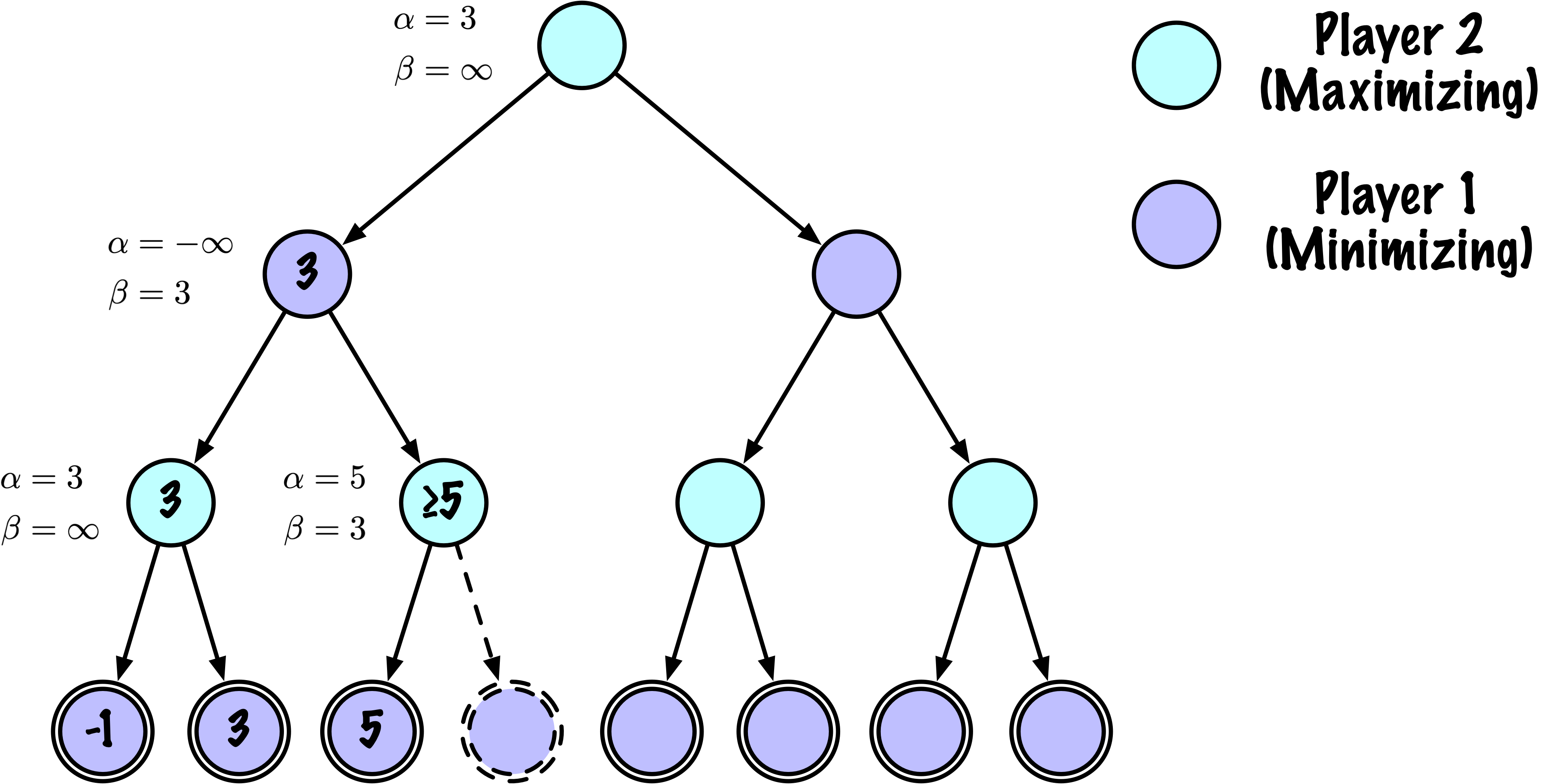
def _alphabeta(self, state, player, maximizing, depth, alpha, beta):
"""
Internal recursive minimax search with alpha–beta pruning.
Parameters
----------
state : NumPy array, current board
player : "X" or "O", the player to move
maximizing : True if this is a maximizing node (X to move)
depth : remaining search depth
alpha : best value found so far for the maximizer
beta : best value found so far for the minimizer
Returns
-------
(value, move)
value : evaluation of the state from X's perspective (+1/-1/0)
move : the best move found at this node
"""
# Instrumentation: count this node
self.nodes_visited += 1
# Terminal test: win/loss/draw or depth cutoff
if self.game.is_terminal(state) or depth == 0:
return self.game.evaluate(state), None
moves = self.game.get_valid_moves(state)
best_move = None
# ------------------------------------------------------------
# Maximizing node (X)
# ------------------------------------------------------------
if maximizing:
value = -math.inf
for move in moves:
next_state = self.game.make_move(state, move, player)
child_val, _ = self._alphabeta(
next_state,
self.game.get_opponent(player),
False, # next is minimizing
depth - 1,
alpha,
beta
)
if child_val > value:
value = child_val
best_move = move
# Update alpha
alpha = max(alpha, value)
# Prune
if beta <= alpha:
break
return value, best_move
# ------------------------------------------------------------
# Minimizing node (O)
# ------------------------------------------------------------
else:
value = math.inf
for move in moves:
next_state = self.game.make_move(state, move, player)
child_val, _ = self._alphabeta(
next_state,
self.game.get_opponent(player),
True, # next is maximizing
depth - 1,
alpha,
beta
)
if child_val < value:
value = child_val
best_move = move
# Update beta
beta = min(beta, value)
# Prune
if beta <= alpha:
break
return value, best_move