Algorithmes d’apprentissage

CSI 4506 - automne 2025

Marcel Turcotte

Version: sept. 16, 2025 10h03

Préamble

Message du jour

Les grands modèles de language (LLM) démontrent des capacités linguistiques remarquables, incitant un nombre croissant d’individus à engager des dialogues personnels avec eux. Murray Shanahan, affilié à Google DeepMind et à l’Imperial College, introduit un cadre intéressant pour examiner le « comportement » de ces modèles. Il conceptualise leurs interactions à travers le prisme du jeu de rôle, comme discuté dans son récent travail publié dans Nature.

• Conscience, raisonnement et philosophie de l’IA avec Murray Shanahan, dans ce podcast de Google DeepMind, Hannah Fry interviewe Murray Shanahan, 2025-04-24.

Selon le contexte de leurs invites d’interaction, ces modèles peuvent adopter des personnages simulant des individus malveillants, pouvant potentiellement offrir des conseils aux conséquences néfastes.

• Quatre robots conversationnels mis à l’épreuve, La Presse, 2029-09-04.

• OpenAI s’efforce d’atténuer la psychose de l’IA et d’éliminer la co-création de délires humain-IA lors de l’utilisation de ChatGPT et GPT-5, par Lance Eliot, Forbes, 2025-09-02.

• Ce qu’il faut savoir sur la « psychose de l’IA » et l’effet des chatbots d’IA sur la santé mentale, PBS News, 2025-08-31.

Voici un rappel pour la page de bien-être de l’Université d’Ottawa, qui offre un éventail complet de ressources, y compris des services de santé médicale et mentale, conçus pour soutenir votre bien-être et celui de votre entourage.

• Santé et bien-être des étudiants

Microsoft boss troubled by rise in reports of ‘AI psychosis’, BBC News, 2025-08-21.

Résultats d’apprentissage

• Différencier entre modèle, objectif et optimiseur dans les algorithmes d’apprentissage.
• Expliquer le KNN pour la classification et la régression, y compris la prédiction uniforme et pondérée par la distance.
• Décrire les arbres de décision et appliquer le critère de division en utilisant des mesures d’impureté telles que le Gini.
• Interpréter les frontières de décision et le concept de séparabilité linéaire.

Comme indiqué dans le cours d’introduction, mon objectif est de présenter une série de concepts menant à l’apprentissage profond. Comme point de départ, la régression linéaire serait un choix logique en tant que premier algorithme d’apprentissage à examiner. Néanmoins, il est tout aussi crucial de posséder une compréhension générale de divers autres algorithmes d’apprentissage, car leurs structures de modèles et leurs processus d’entraînement diffèrent considérablement. Par conséquent, je vais brièvement discuter des k-plus proches voisins (k nearest neighbours) et des arbres de décision, avant d’introduire la régression linéaire.

KNN

k-plus-proches voisins

• KNeighborsClassifier, examples
• KNeighborsRegressor, exemples

Attribution: Nearest Neighbors Classification.

KNN - Apprentissage

• Apprentissage paresseux (lazy learning): pas d’entraînement explicite
• Le “modèle” est le jeu de données

L’algorithme des k plus proches voisins (KNN) stocke simplement ses données d’entraînement. Il n’y a pas d’entraînement explicite. Nous appelons cela “apprentissage paresseux”.

Lorsque le nombre d’exemples est grand, les données de basse dimension peuvent être stockées dans une structure de données spécialisée, telle qu’un kd-tree ou un ball tree, pour accélérer le calcul au moment de l’inférence. Pour les données de haute dimension, des techniques comme les plus proches voisins approximatifs (ANN) ont été développées.

KNN - Inférence

• Classification/régression en fonction des étiquettes/valeurs des \(k\) exemples les plus proches dans l’espace des attributs

Bien que le coût d’inférence puisse sembler faible, puisqu’il est linéaire par rapport au nombre d’exemples, il est important de se rappeler que le flux de travail typique d’un projet d’apprentissage automatique est d’entraîner un modèle une fois et d’utiliser ce modèle pour chaque requête, où le nombre de requêtes peut être assez grand.

Le coût est de \(\mathcal{O}(ND)\) par requête (naïf), où \(N\) = nombre d’exemples, \(D\) = dimensions

Définition formelle

Étant donné un jeu de données \(\{(x_i, y_i)\}_1^{N}\) et un exemple non vu \(x\) :

• Calculer les distances \(d(x, x_i)\)
• Sélectionner les \(k\) plus petites distances
• Classification : vote majoritaire (possiblement pondéré par \(1/d\))
• Régression : moyenne (possiblement pondérée)

L’algorithme des \(k\) plus proches voisins (KNN) est une méthode d’apprentissage simple, non paramétrique et basée sur les instances, utilisée pour la classification et la régression. Il classe un point de données en fonction de l’étiquette majoritaire de ses \(k\) plus proches voisins dans l’espace des attributs, où \(k\) est une constante définie par l’utilisateur. Des métriques de distance comme la distance euclidienne sont couramment utilisées pour déterminer les plus proches voisins.

Dans le contexte de la régression, la valeur prédite \(\hat{y}(x)\) est calculée comme une somme pondérée des étiquettes de ses \(k\) plus proches voisins. Les poids peuvent être uniformes ou basés sur la distance, reflétant la proximité de chaque voisin par rapport à la requête \(x\).

Pour une requête \(x\), supposons que ses \(k\) plus proches voisins ont des cibles (étiquettes) \(y_1, \dots, y_k\) et des distances \(d_1, \dots, d_k\).

• Poids uniformes (par défaut) :

\[ \hat{y}(x) = \frac{1}{k} \sum_{i=1}^k y_i \]

• Poids basés sur la distance (l’option intégrée "distance") :

\[ \hat{y}(x) = \frac{\sum_{i=1}^k \frac{1}{d_i} \, y_i}{\sum_{i=1}^k \frac{1}{d_i}} \]

Dans ce qui précède, à mesure que la distance \(d_i\) entre l’exemple \(x_i\) et l’exemple \(x\) augmente, le réciproque \(\frac{1}{d_i}\) diminue. En conséquence, les exemples qui sont plus éloignés de \(x\) exercent moins d’influence sur le résultat prédit, \(\hat{y}(x)\).

Dans les deux cas, la propriété de combinaison convexe garantit que :

\[ \min(y_1, \dots, y_k) \;\; \leq \;\; \hat{y}(x) \;\; \leq \;\; \max(y_1, \dots, y_k). \]

Un algorithme non paramétrique ne fait aucune hypothèse sur la distribution sous-jacente des données et n’apprend pas un ensemble fixe de paramètres ou un modèle pendant la phase d’entraînement. Au lieu de cela, il s’appuie directement sur les données d’entraînement pour prendre des décisions au moment de la classification ou de la régression, ce qui le rend flexible et adaptable à diverses formes de données, mais potentiellement coûteux en termes de calcul au moment de la prédiction.

KNN présente des limitations claires :

1. Coût computationnel
   • La prédiction nécessite de calculer les distances vers tous les points d’apprentissage, \(O(n)\) par requête.
2. Malédiction de la dimensionnalité
   • Dans les espaces de haute dimension, les métriques de distance perdent leur pouvoir discriminant.
3. Choix de \(k\) et de la métrique de distance
   • Petit \(k\) : forte variance, sensible au bruit/aux valeurs aberrantes.
   • Grand \(k\) : fort biais, sur-lissage.
4. Sensibilité à l’échelle des caractéristiques
   • Les distances dépendent de l’échelle ; les variables avec des plages plus grandes dominent à moins que les caractéristiques ne soient normalisées/standardisées.
5. Données déséquilibrées
   • En classification, si une classe est beaucoup plus fréquente, KNN peut être biaisé vers cette classe, car les voisins ont plus de chances de lui appartenir.
6. Non extrapolatif
   • Les prédictions sont toujours des combinaisons convexes (en régression) ou des votes majoritaires (en classification) des étiquettes d’apprentissage.
   • Cela signifie que KNN ne peut pas extrapoler des tendances en dehors de la plage des données d’apprentissage observées.

Dans scikit-learn, plusieurs modèles sont couramment utilisés pour les tâches de régression. Voici quelques-uns des principaux modèles :

1. Régression Linéaire (LinearRegression) :
   • Une approche linéaire simple qui modélise la relation entre les variables indépendantes et la variable dépendante en ajustant une équation linéaire aux données observées.
2. Régression à Vecteurs de Support (SVR) :
   • Une extension des Machines à Vecteurs de Support (SVM) pour les tâches de régression, qui essaie d’ajuster la meilleure ligne dans une marge de tolérance spécifiée.
3. Régression par Arbre de Décision (DecisionTreeRegressor) :
   • Utilise des arbres de décision pour modéliser la relation entre les caractéristiques d’entrée et la variable cible en divisant récursivement les données en sous-ensembles.
4. Régression par Forêt Aléatoire (RandomForestRegressor) :
   • Une méthode d’ensemble qui utilise plusieurs arbres de décision pour améliorer la précision prédictive et contrôler le surapprentissage.
5. Régression par Gradient Boosting (GradientBoostingRegressor) :
   • Une autre méthode d’ensemble qui construit des arbres de décision séquentiels, où chaque arbre corrige les erreurs du précédent.
6. Régression par les K-Plus Proches Voisins (KNeighborsRegressor) :
   • Une méthode non paramétrique qui prédit la variable cible en se basant sur la moyenne des k-plus proches voisins dans l’espace des caractéristiques.

Ces modèles offrent une gamme d’approches pour gérer différents types de problèmes de régression, chacun avec ses propres forces et applications adaptées.

Exercices

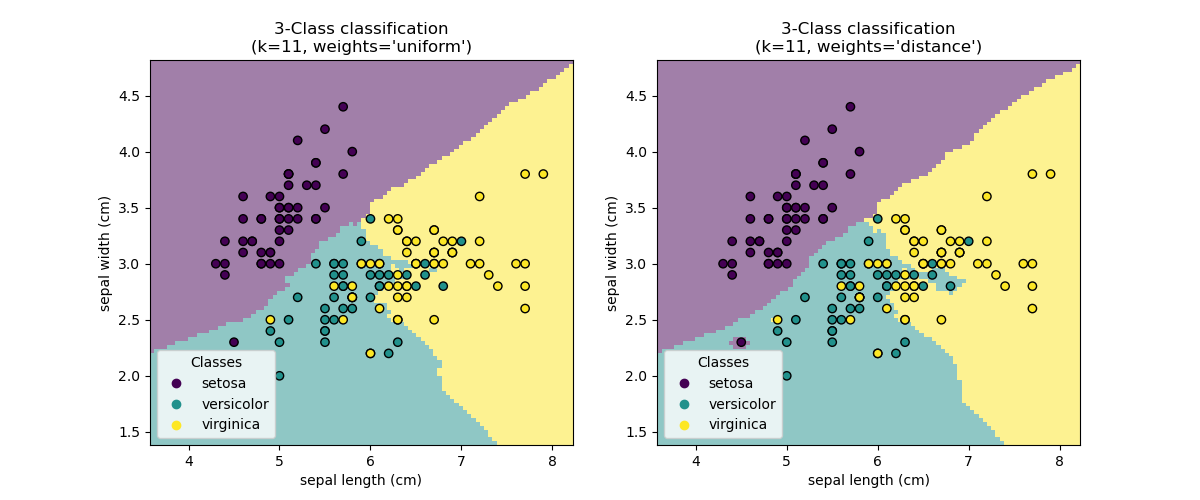
Téléchargez ces exemples pour expérimenter avec des variations de code. Notamment, examinez comment les changements de \(k\) influencent les frontières de décision en classification et la douceur de la ligne de régression.

• Nearest Neighbors Classification
• Nearest Neighbors Regression
• Importance of Feature Scaling

Le site web de scikit-learn propose des exemples en format Jupyter Notebook, accessibles via des navigateurs de bureau avec des liens sur la droite.

Arbre de Décision

Interprétable

Les arbres de décision sont précieux car ils délimitent clairement les règles apprises par le modèle. L’arbre de décision ci-dessus illustre les résultats d’une étude examinant les symptômes d’anxiété cliniquement significatifs. Dans ce cas, le déterminant initial était de savoir si les étudiants rapportaient avoir un environnement familial positif.

Attribution : Agence de la santé publique du Canada

Qu’est-ce qu’un arbre de décision ?

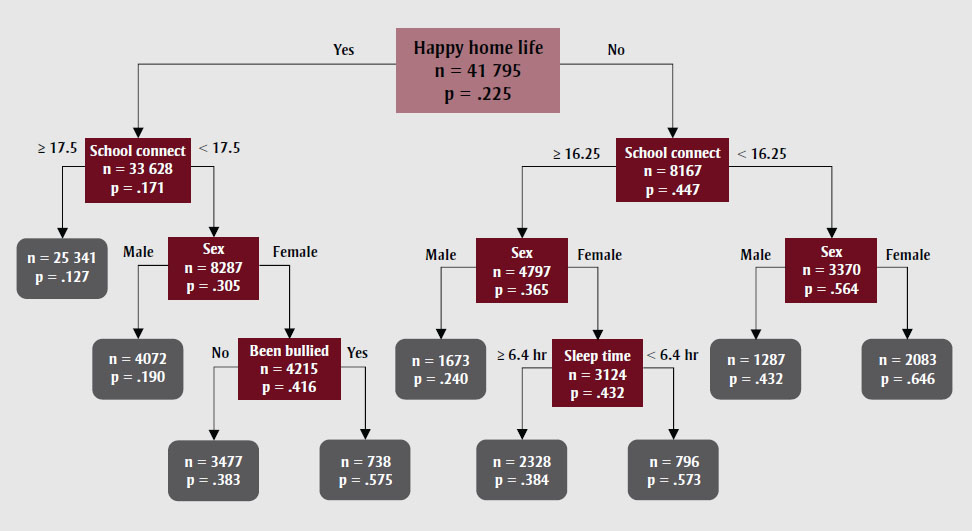
• Un arbre de décision est une structure hiérarchique représentée sous forme de graphe orienté acyclique, utilisée pour les tâches de classification et de régression.
• Chaque nœud interne effectue un test binaire sur un attribut particulier (\(j\)), tel que si le nombre de connexions dans une école dépasse un seuil spécifié.
• Les feuilles fonctionnent comme des nœuds de décision.

Les arbres de décision peuvent aller au-delà des divisions binaires, comme le démontrent des algorithmes tels que ID3, qui permettent des nœuds avec plusieurs enfants.

La structure de l’arbre est inférée (apprise) à partir des données d’entraînement.

Classification de nouvelles instances (Inférence)

• Commencez par le nœud racine de l’arbre de décision. Procédez en répondant à une série de questions binaires jusqu’à atteindre un nœud feuille. L’étiquette associée à cette feuille indique la classification de l’instance.
• Alternativement, certains algorithmes peuvent stocker une distribution de probabilité au niveau de la feuille, représentant la fraction d’échantillons d’entraînement correspondant à chaque classe \(k\), parmi toutes les classes possibles \(k\).

Lorsqu’un arbre de décision est utilisé pour résoudre une tâche de régression, chaque nœud feuille stocke une valeur prédite. Plus précisément :

\[ \hat{y}_\text{feuille} = \frac{1}{N_\text{feuille}} \sum_{i \in \text{feuille}} y_i, \]

où \(N_\text{feuille}\) est le nombre d’échantillons d’entraînement qui se retrouvent dans cette feuille, et \(y_i\) sont leurs valeurs cibles.

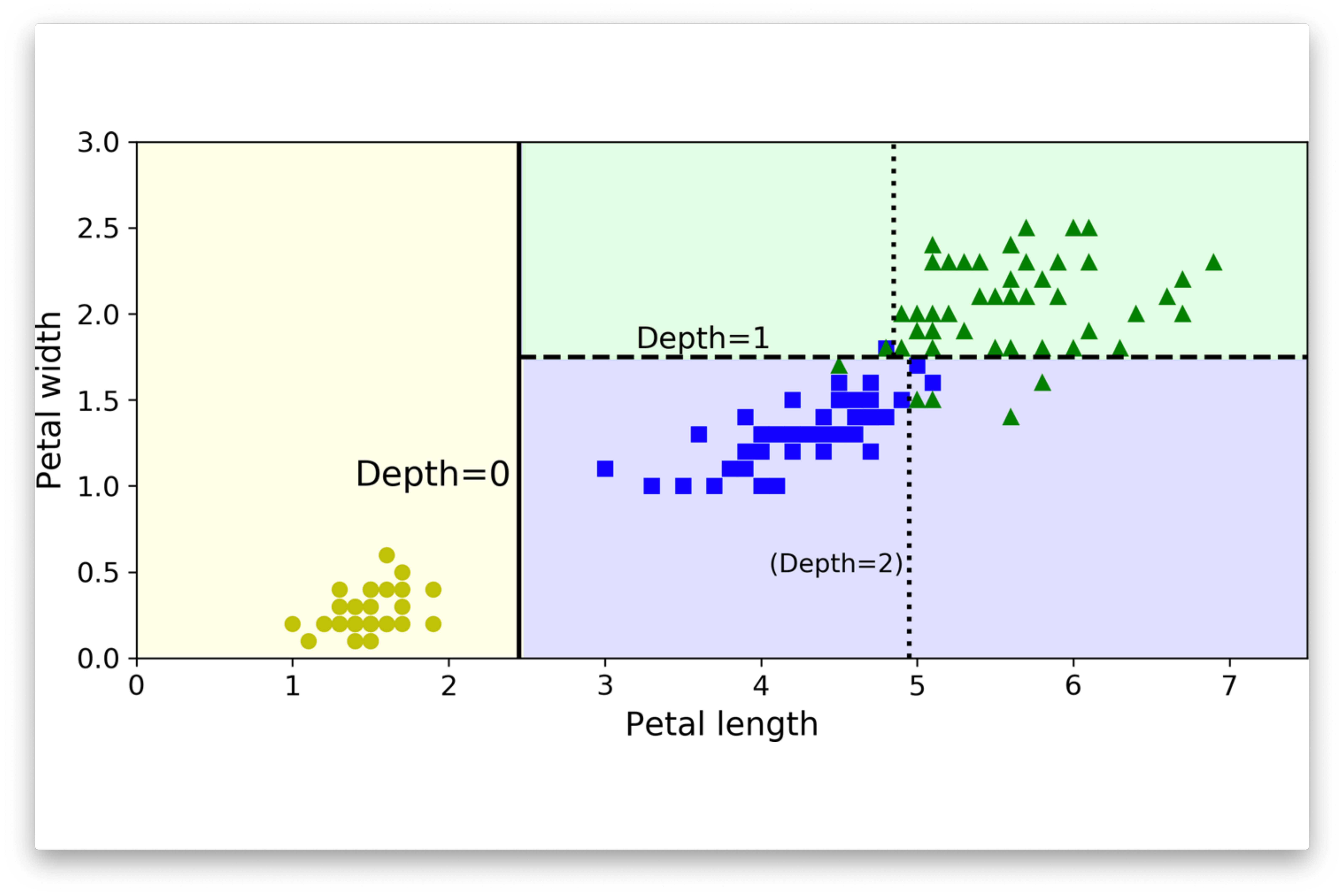
Frontière de décision

Manchots de Palmer

# Chargement de notre jeu de données

try:
  from palmerpenguins import load_penguins
except:
  ! pip install palmerpenguins
  from palmerpenguins import load_penguins

penguins = load_penguins()

# Pairplot avec seaborn

import matplotlib.pyplot as plt
import seaborn as sns

sns.pairplot(penguins, hue='species', markers=["o", "s", "D"])
plt.suptitle("Graphiques de dispersion par paires des attributs des manchots")
plt.show()

Manchots de Palmer

Problème de classification binaire

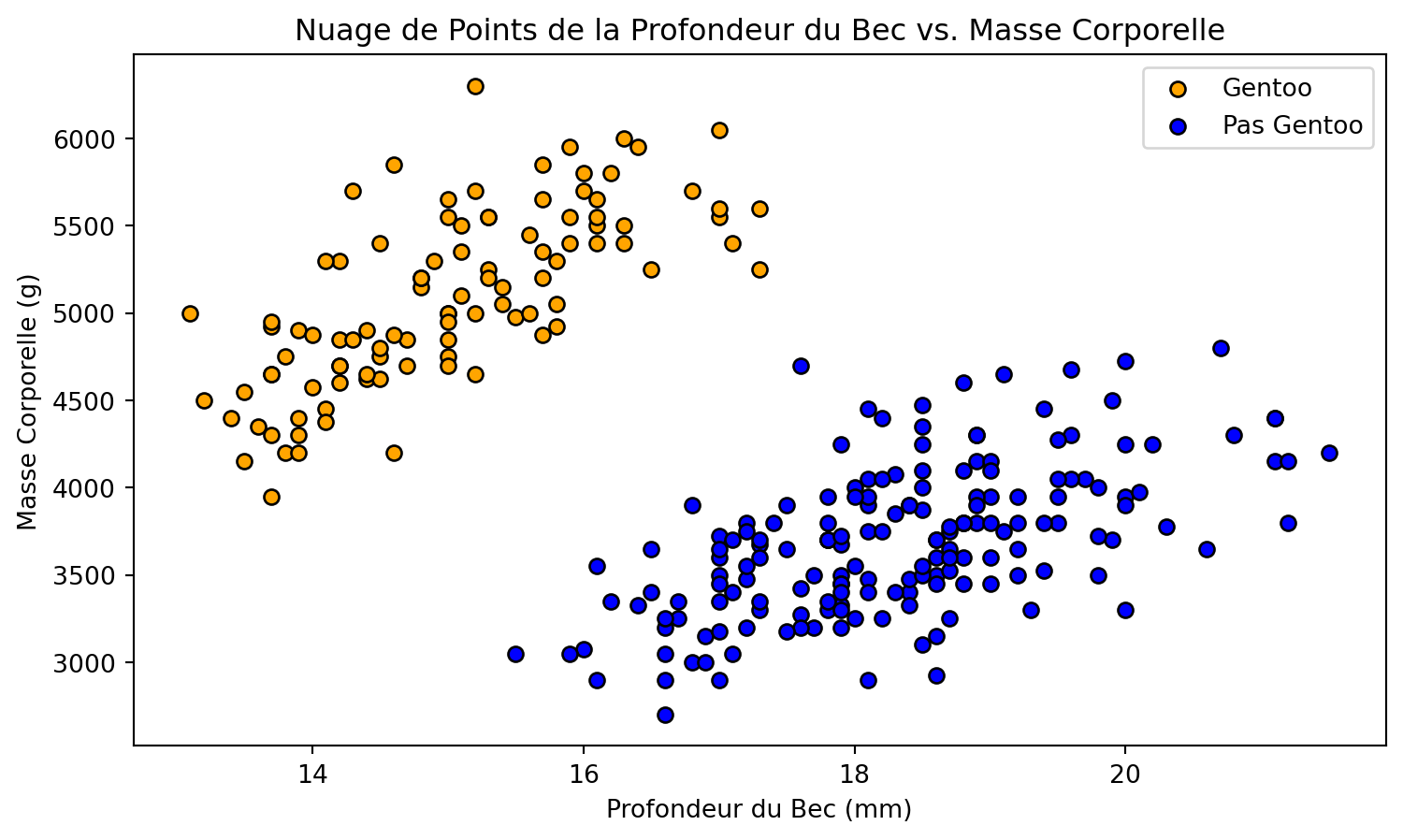
• Plusieurs graphiques de dispersion révèlent un regroupement distinct des instances Gentoo.
• Pour illustrer notre prochain exemple, nous proposons un modèle de classification binaire : Gentoo contre non-Gentoo.
• Notre analyse se concentrera sur deux attributs clés : masse corporelle et profondeur du bec.

Définition

Une frontière de décision est une “frontière” qui partitionne l’espace des attributs sous-jacent en régions correspondant à différentes étiquettes de classe.

Le terme frontière sera clarifié dans les prochaines diapositives.

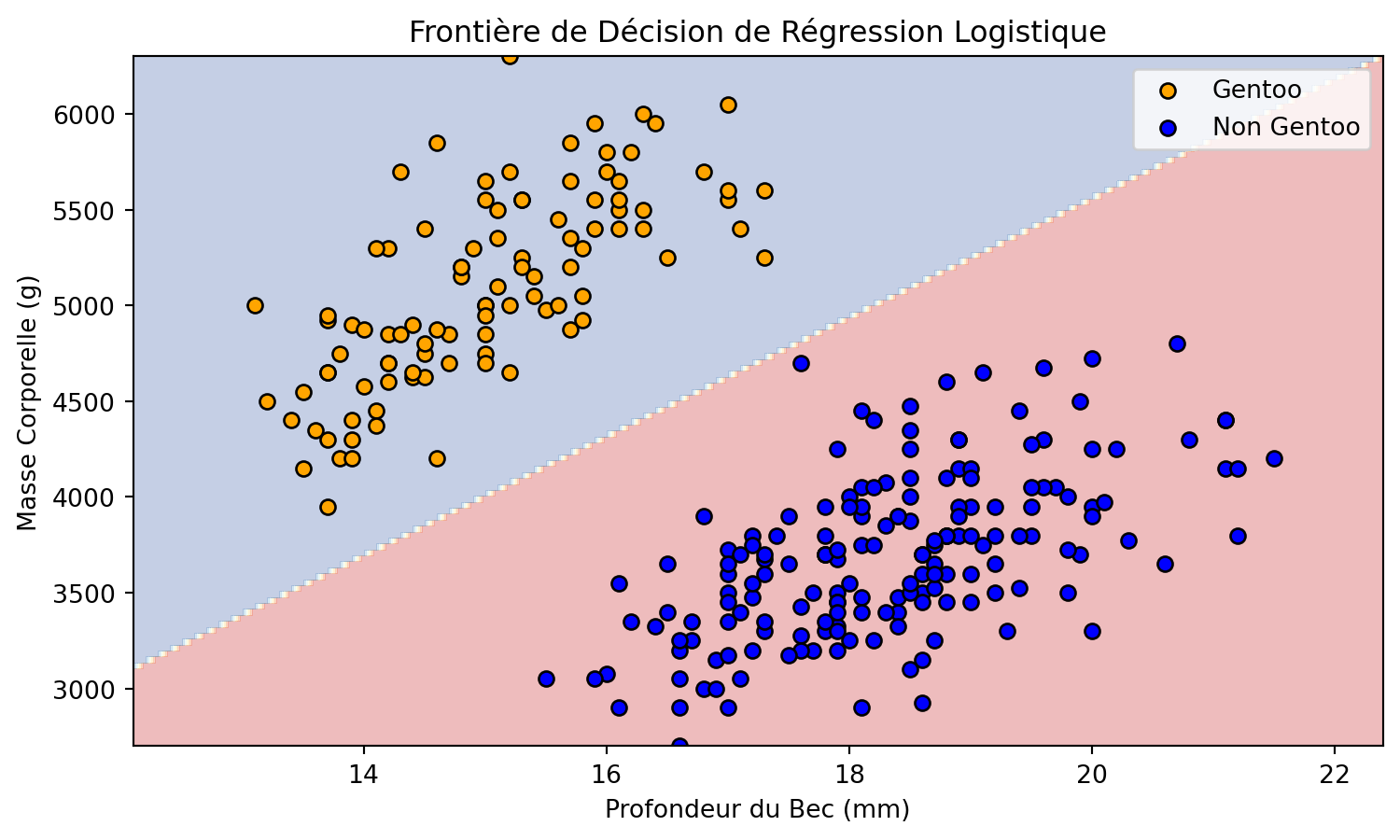
Frontière de décision

La frontière de décision entre ces attributs peut être représentée comme une ligne.

# Importer les bibliothèques nécessaires
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split

try:
  from palmerpenguins import load_penguins
except:
  ! pip install palmerpenguins
  from palmerpenguins import load_penguins

# Charger le jeu de données Palmer Penguins
df = load_penguins()

# Conserver uniquement les attributs nécessaires : 'bill_depth_mm' et 'body_mass_g'
features = ['bill_depth_mm', 'body_mass_g']
df = df[features + ['species']]

# Supprimer les lignes avec des valeurs manquantes
df.dropna(inplace=True)

# Créer un problème binaire : 'Gentoo' contre 'Pas Gentoo'
df['species_binary'] = df['species'].apply(lambda x: 1 if x == 'Gentoo' else 0)

# Définir la matrice de attributs X et le vecteur cible y
X = df[features].values
y = df['species_binary'].values

# Diviser les données en ensembles d'entraînement et de test
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Fonction pour tracer le nuage de points initial
def plot_scatter(X, y):
    plt.figure(figsize=(9, 5))
    plt.scatter(X[y == 1, 0], X[y == 1, 1], color='orange', edgecolors='k', marker='o', label='Gentoo')
    plt.scatter(X[y == 0, 0], X[y == 0, 1], color='blue', edgecolors='k', marker='o', label='Pas Gentoo')
    plt.xlabel('Profondeur du Bec (mm)')
    plt.ylabel('Masse Corporelle (g)')
    plt.title('Nuage de Points de la Profondeur du Bec vs. Masse Corporelle')
    plt.legend()
    plt.show()
    
# Tracer le nuage de points initial
plot_scatter(X_train, y_train)

Frontière de décision

Frontière de décision

La frontière de décision entre ces attributs peut être représentée par une ligne.

# Entraîner un modèle de régression logistique
model = LogisticRegression()
model.fit(X_train, y_train)

# Fonction pour tracer la frontière de décision
def plot_decision_boundary(X, y, model):
    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),
                         np.arange(y_min, y_max, 0.1))
    Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    
    plt.figure(figsize=(9, 5))
    plt.contourf(xx, yy, Z, alpha=0.3, cmap='RdYlBu')
    plt.scatter(X[y == 1, 0], X[y == 1, 1], color='orange', edgecolors='k', marker='o', label='Gentoo')
    plt.scatter(X[y == 0, 0], X[y == 0, 1], color='blue', edgecolors='k', marker='o', label='Non Gentoo')
    plt.xlabel('Profondeur du Bec (mm)')
    plt.ylabel('Masse Corporelle (g)')
    plt.title('Frontière de Décision de Régression Logistique')
    plt.legend()
    plt.show()

# Tracer la frontière de décision sur l'ensemble d'entraînement
plot_decision_boundary(X_train, y_train, model)

Frontière de décision

Définition

On dit que les données sont linéairement séparables lorsque deux classes de données peuvent être parfaitement séparées par une unique frontière linéaire, telle qu’une droite dans un espace bidimensionnel ou un hyperplan dans des dimensions supérieures.

Frontière de décision simple

(a) données d’entraînement, (b) courbe quadratique, et (c) fonction linéaire.

Attribution : (Geurts, Irrthum, et Wehenkel 2009)

Le tableau de gauche présente des données d’entraînement pour une tâche hypothétique de classification binaire dans un contexte médical, où les deux attributs, \(X_1\) et \(X_2\), sont utilisés pour prédire la variable cible, \(y\), qui peut prendre deux valeurs : malade et sain. Vous pouvez imaginer que \(X_1\) et \(X_2\) sont des mesures, telles que la pression artérielle et le rythme cardiaque ou les niveaux de cholestérol et de glucose.

La régression logistique (c) utilise une frontière de décision linéaire. Dans cet exemple précis, la frontière de décision est représentée par une ligne droite. L’emploi de la régression logistique pour ce problème entraîne plusieurs erreurs de classification : les points rouges au-dessus de la ligne, qui devraient être classés comme ‘malade’, sont incorrectement prédits comme ‘sain’. Inversement, les points verts en dessous de la ligne, qui devraient être classés comme ‘sain’, sont incorrectement prédits comme ‘malade’.

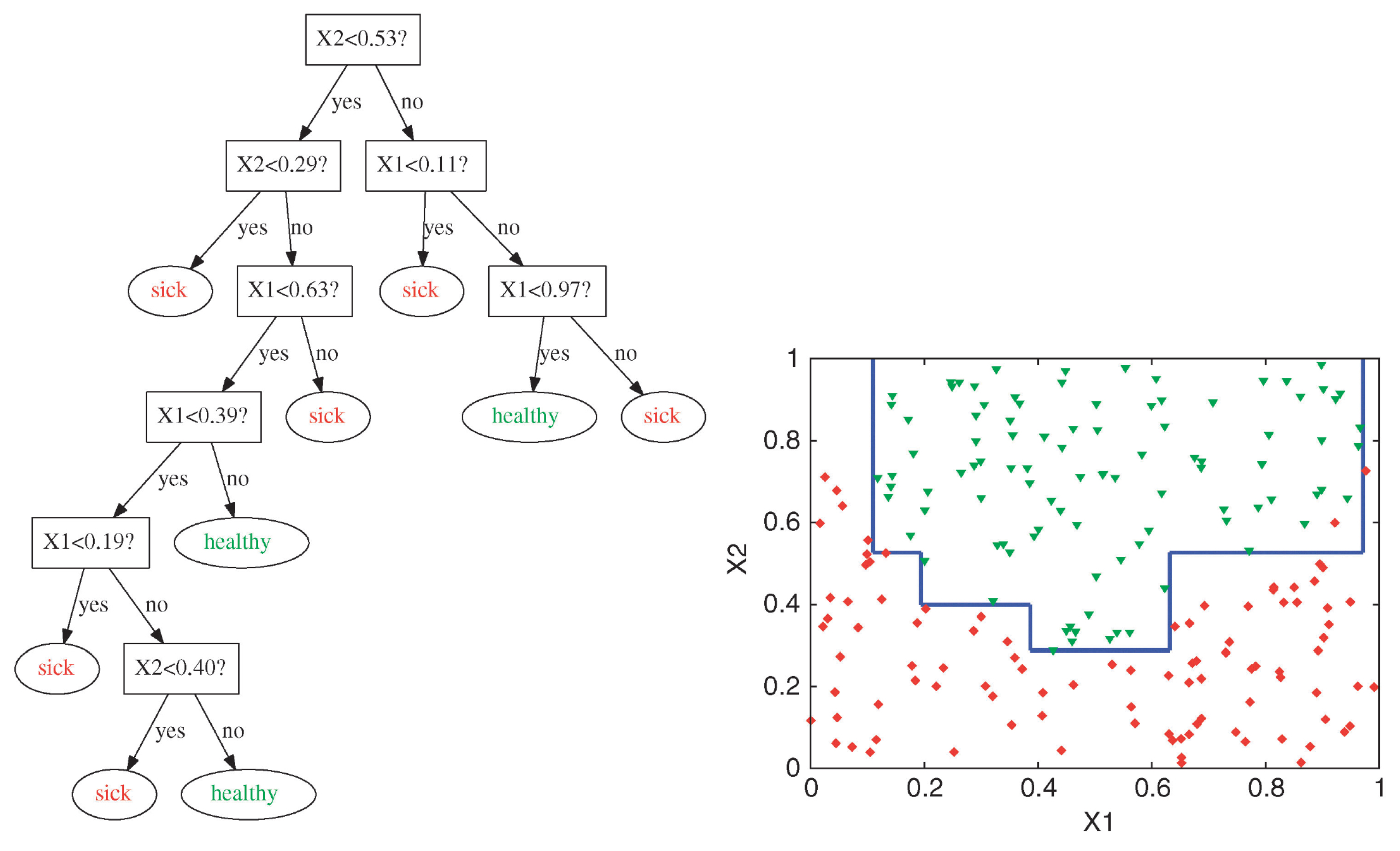
Frontière de décision complexe

Les arbres de décision sont capables de générer des frontières de décision irrégulières et non linéaires.

Attribution : ibidem.

Assurez-vous de comprendre les relations entre les huit règles de décision délimitées dans l’arbre de décision et les neuf segments de ligne représentés dans le nuage de points.

Définition (révisée)

Une frontière de décision est une hypersurface qui partitionne l’espace des caractéristiques sous-jacent en régions correspondant à différentes étiquettes de classe.

Arbre de décision (suite)

Construire un arbre de décision

• Comment construire (apprendre) un arbre de décision ?
• Y a-t-il des arbres qui sont “meilleurs” que d’autres ?
• Est-il possible de construire un arbre de décision optimal de manière efficace sur le plan computationnel ?

(Hyafil et Rivest 1976)

Optimalité

• Soit \(X = \{x_1, \ldots, x_n\}\) un ensemble fini d’objets.
• Soit \(\mathcal{T} = \{T_1, \ldots, T_t\}\) un ensemble fini de tests.
• Pour chaque objet et test, nous avons :
  • \(T_i(x_j)\) est soit vrai soit faux.
• Un arbre optimal est celui qui identifie complètement tous les objets dans \(X\) et pour lequel \(|T|\) est minimal.

Hyafil et Rivest (1976) a démontré que la construction d’arbres de décision binaires optimaux est un problème NP-Complet.

(Hyafil et Rivest 1976)

Construction d’un arbre de décision

• Développement itératif : Commencez avec un arbre vide. Introduisez progressivement des nœuds, chacun informé par le jeu de données d’entraînement, jusqu’à ce que le jeu de données soit complètement classé ou que d’autres critères d’arrêt, tels que la profondeur maximale de l’arbre, soient atteints.

L’apprentissage est le processus de construction de l’arbre à partir des données d’entraînement.

Construction d’un arbre de décision

• Construction initiale du nœud :
  • Pour établir le nœud racine, évaluez toutes les \(D\) attributs disponibles.
    • Pour chaque attributs, évaluez différentes valeurs seuils dérivées des données observées dans le jeu d’entraînement.

Construction d’un arbre de décision

• Pour un attribut numérique, l’algorithme considère tous les points de division possibles (seuils) dans la plage de l’attribut.
• Ces points de division sont généralement les milieux entre deux valeurs uniques triées consécutives de l’attribut.

Construction d’un arbre de décision

• Pour un attribut catégoriel avec \(k\) valeurs uniques, l’algorithme considère toutes les manières possibles de diviser les catégories en deux groupes.
• Par exemple, si l’attribut (prévision météorologique) a les valeurs ‘Pluvieux’, ‘Nuageux’ et ‘Ensoleillé’, il évalue les divisions suivantes :
  • \(\{\mathrm{Pluvieux}\}\) vs. \(\{\mathrm{Nuageux}, \mathrm{Ensoleillé}\}\),
  • \(\{\mathrm{Nuageux}\}\) vs. \(\{\mathrm{Pluvieux}, \mathrm{Ensoleillé}\}\),
  • \(\{\mathrm{Ensoleillé}\}\) vs. \(\{\mathrm{Pluvieux}, \mathrm{Nuageux}\}\).

Évaluation

Qu’est-ce qui définit une “bonne” séparation des données ?

• \(\{\mathrm{Pluvieux}\}\) vs. \(\{\mathrm{Nuageux}, \mathrm{Ensoleillé}\}\) : \([20,10,5]\) et \([10,10,15]\).
• \(\{\mathrm{Nuageux}\}\) vs. \(\{\mathrm{Pluvieux}, \mathrm{Ensoleillé}\}\) : \([40,0,0]\) et \([0,30,0]\).

Où \([20,10,5]\) indique que le sous-groupe contient 20 exemples de ‘Mauvais’, 10 pour ‘Moyen’, et 5 pour ‘Excellent’, pour que notre modèle prédictif puisse classifier la probabilité d’une journée de pêche réussie.

Évaluation

• Hétérogénéité (également appelée impureté) et homogénéité sont des mesures pour évaluer la composition des partitions de données résultantes.

• Idéalement, chacune de ces partitions devrait contenir des entrées de données d’une seule classe pour atteindre une homogénéité maximale.

• L’entropie et l’indice de Gini sont deux mesures largement utilisées pour évaluer ces caractéristiques.

Évaluation

Fonction objective pour sklearn.tree.DecisionTreeClassifier (CART) :

\[ J(k,t_k) = \frac{N_{\text{gauche}}}{N_{\text{parent}}} G_{\text{gauche}} + \frac{N_{\text{droite}}}{N_{\text{parent}}} G_{\text{droite}} \]

• Le coût de la partition des données en utilisant l’attribut \(k\) et le seuil \(t_k\).

• \(N_{\text{gauche}}\) et \(N_{\text{droite}}\) sont le nombre d’exemples dans les sous-ensembles gauche et droite, respectivement, et \(N_{\text{parent}}\) est le nombre d’exemples avant la division des données.

• \(G_{\text{gauche}}\) et \(G_{\text{droite}}\) sont l’impureté des sous-ensembles gauche et droite, respectivement.

Minimiser ou maximiser \(J\) ?

Indice de Gini

• Indice de Gini (par défaut)

\[ G_i = 1 - \sum_{k=1}^n p_{i,k}^2 \]

• \(p_{i,k}\) est la proportion des exemples de cette classe \(k\) dans le nœud \(i\).

• Quelle est la valeur maximale de l’indice de Gini ?

• La valeur de l’indice de Gini est maximale lorsque toutes les classes sont équiprobables, c’est-à-dire que les proportions sont les mêmes.

• Pour une classification binaire, \(1 - [\frac{1}{2}^2 + \frac{1}{2}^2] = 0.5\).

• Pour le cas général, \(1 - n \times \frac{1}{n}^2 = 1 - \frac{1}{n}\), lorsque \(n \to \infty\), \(\frac{1}{n} \to 0\), l’indice de Gini tend vers 1.

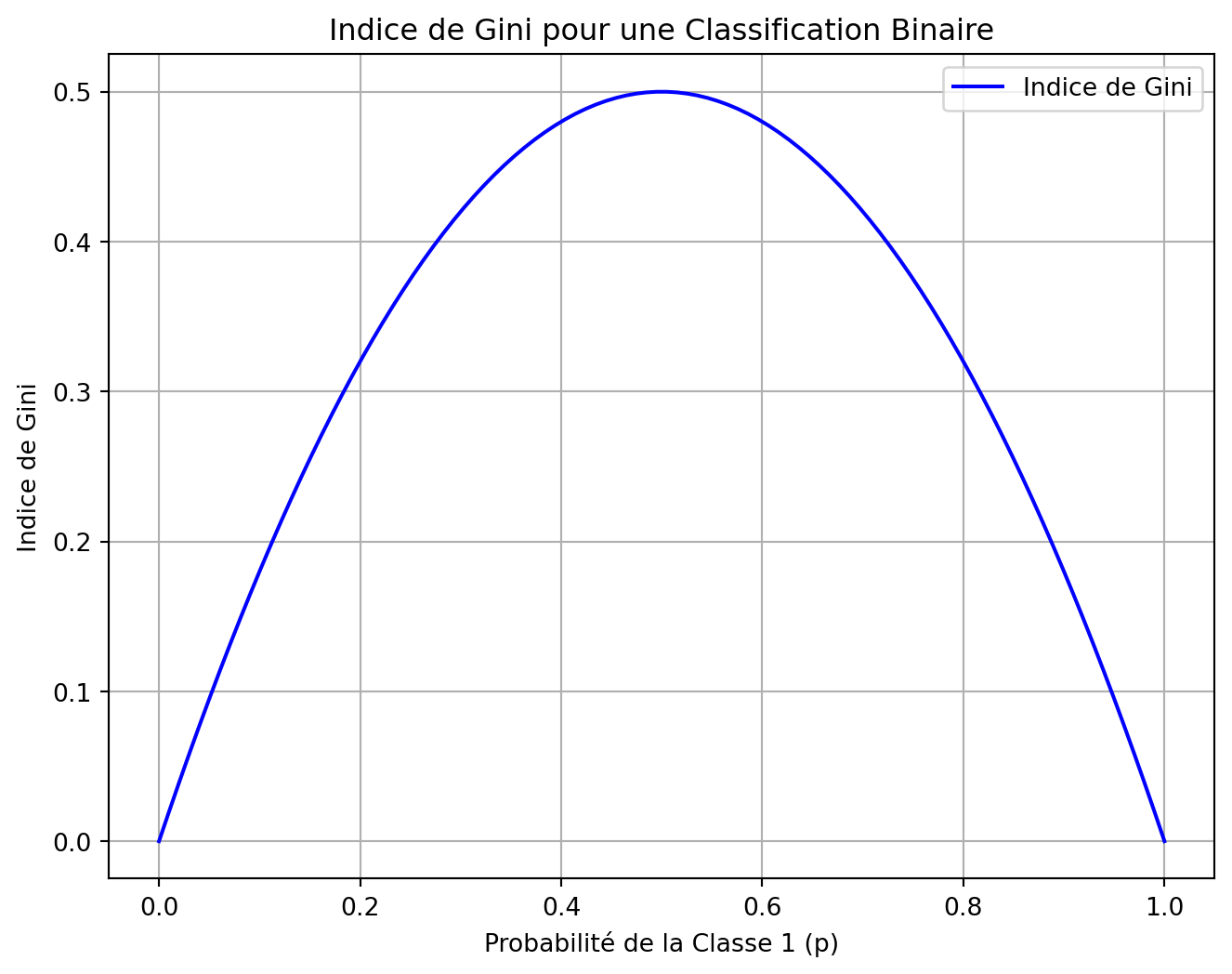
Indice de Gini

Considérant un problème de classification binaire :

• \(1 - [(0/100)^2 + (100/100)^2] = 0\) (pur)
• \(1 - [(25/100)^2 + (75/100)^2] = 0.375\)
• \(1 - [(50/100)^2 + (50/100)^2] = 0.5\)

Basé sur ce qui précède, résolvons-nous un problème de minimisation ou de maximisation ?

Lorsque le problème est formulé comme suit :

• Pour chaque séparation candidate \((k, t_k)\), calculez

\[ J(k,t_k) = \frac{N_{\text{gauche}}}{N_{\text{parent}}} G_{\text{gauche}} + \frac{N_{\text{droite}}}{N_{\text{parent}}} G_{\text{droite}} \]

• L’algorithme choisit ensuite la séparation avec le \(J\) le plus bas, c’est-à-dire la séparation qui donne l’impureté pondérée la plus petite.

De nombreux manuels préfèrent maximiser la réduction d’impureté (gain d’information), qui est simplement

\[ \Delta G = G_{\text{parent}} - J(k,t_k). \]

Maximiser \(\Delta G\) présente des avantages.

Si aucune séparation potentielle pour un nœud parent donné ne conduit à une réduction de l’impureté, le processus récursif de séparation des nœuds s’arrête. Dans ce scénario, la performance de classification du nœud parent dépasse celle de toute séparation possible.

Si l’algorithme envisage de diviser un nœud parent, cela signifie que \(G_{\text{parent}} > 0\), sinon le processus se serait arrêté.

Qu’en est-il de \(\frac{N_{\text{gauche}}}{N_{\text{parent}}}\) et \(\frac{N_{\text{droite}}}{N_{\text{parent}}}\) ?

Que se passe-t-il si le nombre d’exemples dans un enfant est très petit ?

Supposons que nous isolions 1 échantillon (pur) dans l’enfant gauche, et laissons \(N-1\) mélangés dans l’enfant droit.

• Enfant gauche : \(G_{\text{gauche}} = 0\), poids = \(1/N\).
• Enfant droit : \(G_{\text{droite}} \approx G_{\text{parent}}\), pondéré par \((N-1)/N\).

Ainsi \[ J(k,t_k) \;\approx\; \frac{N-1}{N} \, G_{\textrm{parent}} , \]

donc

\[ \Delta \;\approx\; \, G_{\textrm{parent}} - \frac{N-1}{N} \, G_{\textrm{parent}} = \frac{1}{N} \, G_{\textrm{parent}}. \]

C’est seulement un petit gain (diminue à mesure que \(N\) augmente).

Indice de Gini

def gini_index(p):
    """Calculer l'indice de Gini."""
    return 1 - (p**2 + (1 - p)**2)

# Valeurs de probabilité pour la classe 1
p_values = np.linspace(0, 1, 100)

# Calculer l'indice de Gini pour chaque probabilité
gini_values = [gini_index(p) for p in p_values]

# Tracer l'indice de Gini
plt.figure(figsize=(8, 6))
plt.plot(p_values, gini_values, label='Indice de Gini', color='b')
plt.title('Indice de Gini pour une Classification Binaire')
plt.xlabel('Probabilité de la Classe 1 (p)')
plt.ylabel('Indice de Gini')
plt.grid(True)
plt.legend()
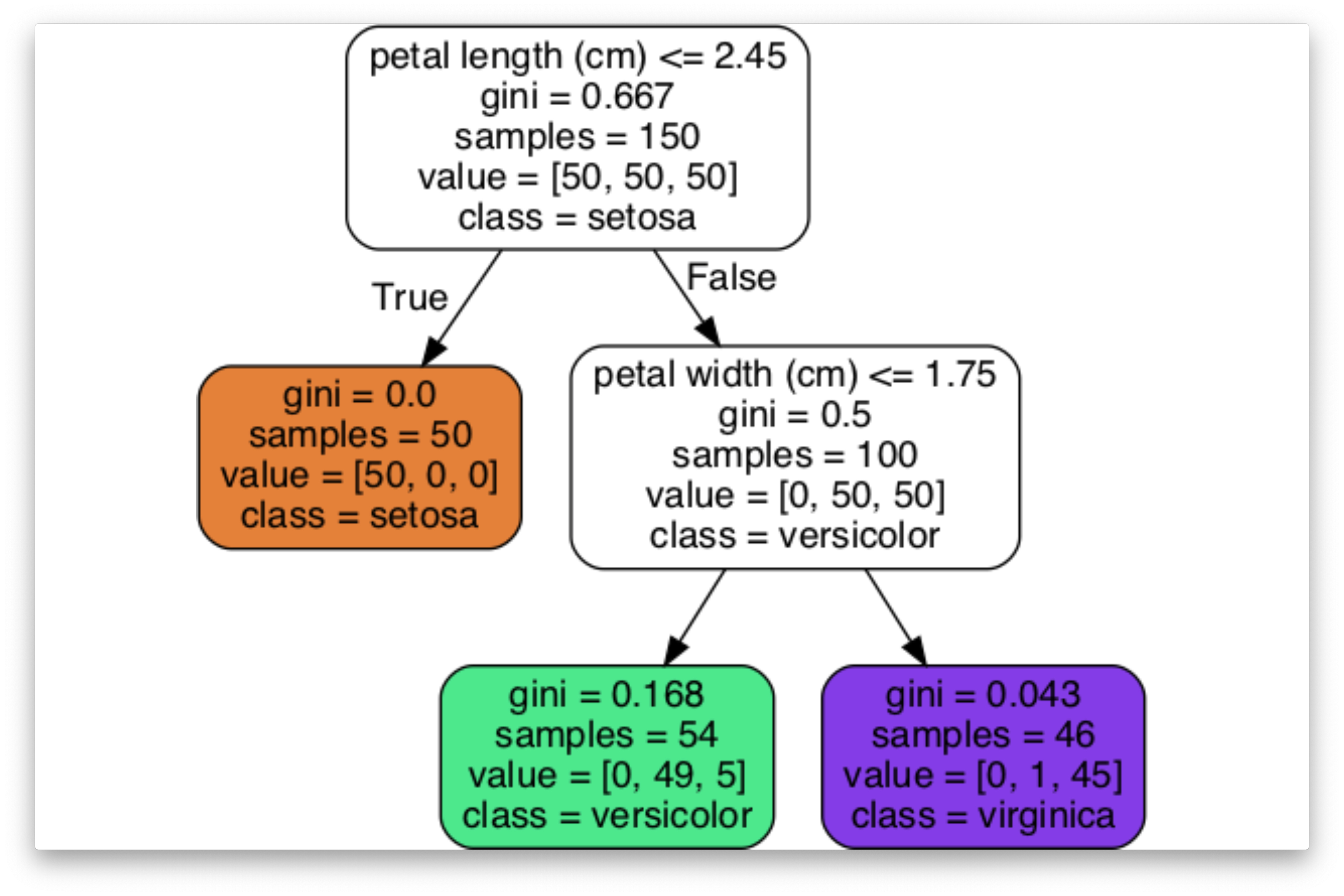
plt.show()

Jeu de données Iris

Attribution : (Géron 2019), Figures 6.1 et 6.2

Exemple complet

Arbres de Décision et de Classification, Explication Claire !!!, (18 m 7s) StatQuest, 2021-04-26

Critères d’arrêt

• Tous les exemples dans un nœud donné appartiennent à la même classe.
• La profondeur de l’arbre dépasserait max_depth.
• Le nombre d’exemples dans le nœud est min_sample_split ou moins.
• Aucune des divisions ne réduit suffisamment l’impureté (min_impurity_decrease).
• Voir la documentation pour d’autres critères.

Limitations

• Peut créer des arbres de grande taille
  • Défi pour l’interprétation
  • Surapprentissage
• Algorithme gourmand, aucune garantie de trouver l’arbre optimal. (Hyafil et Rivest 1976)
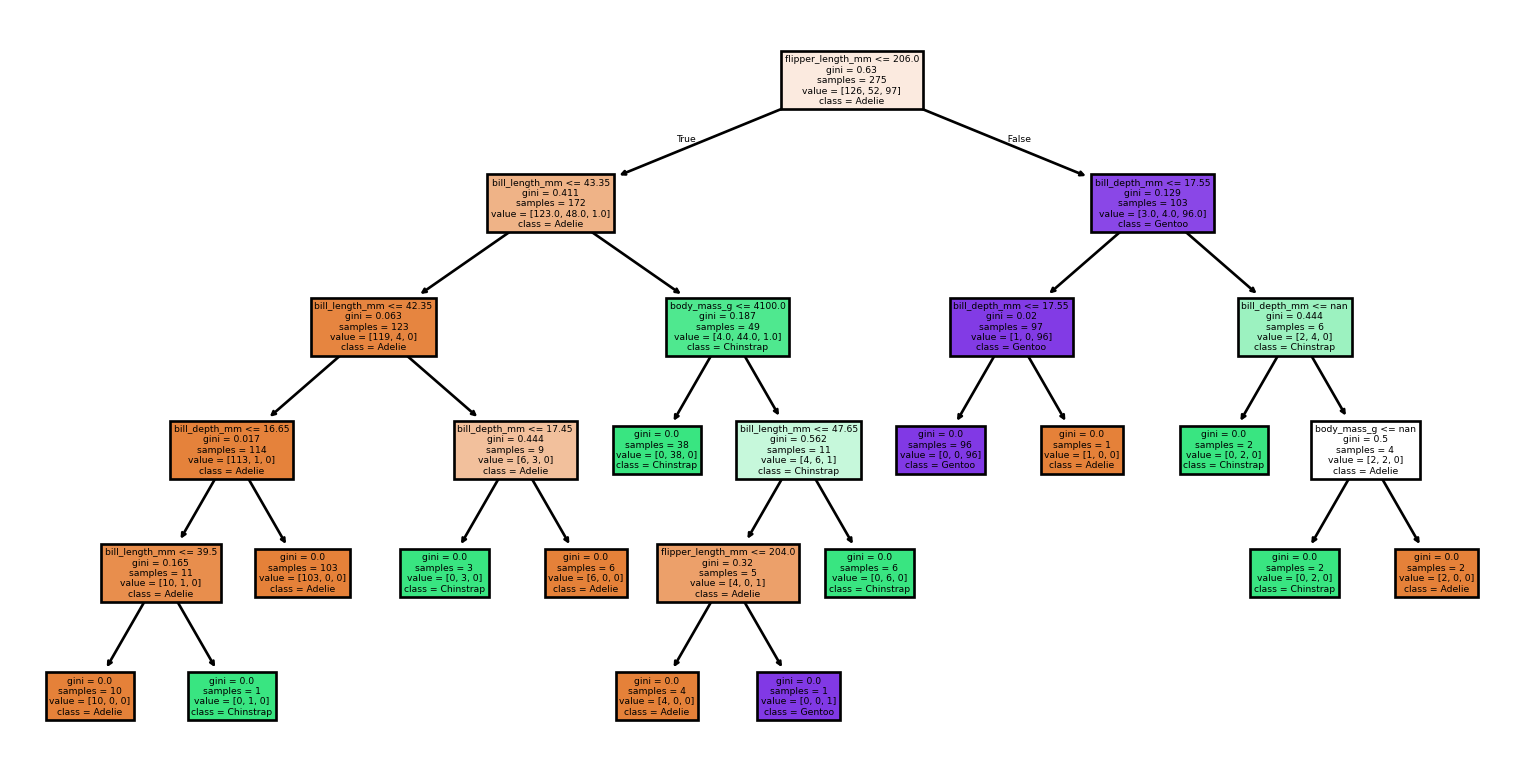
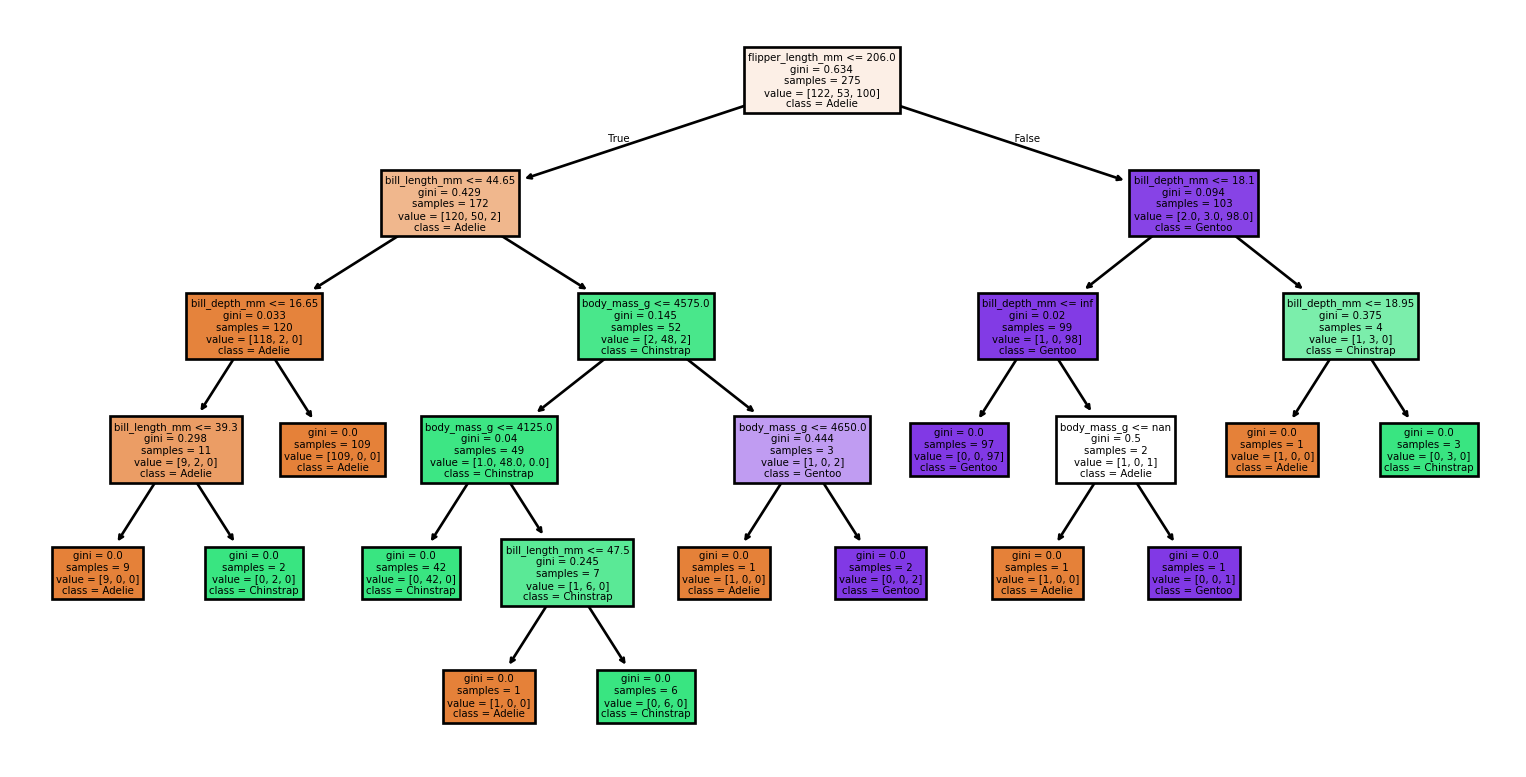
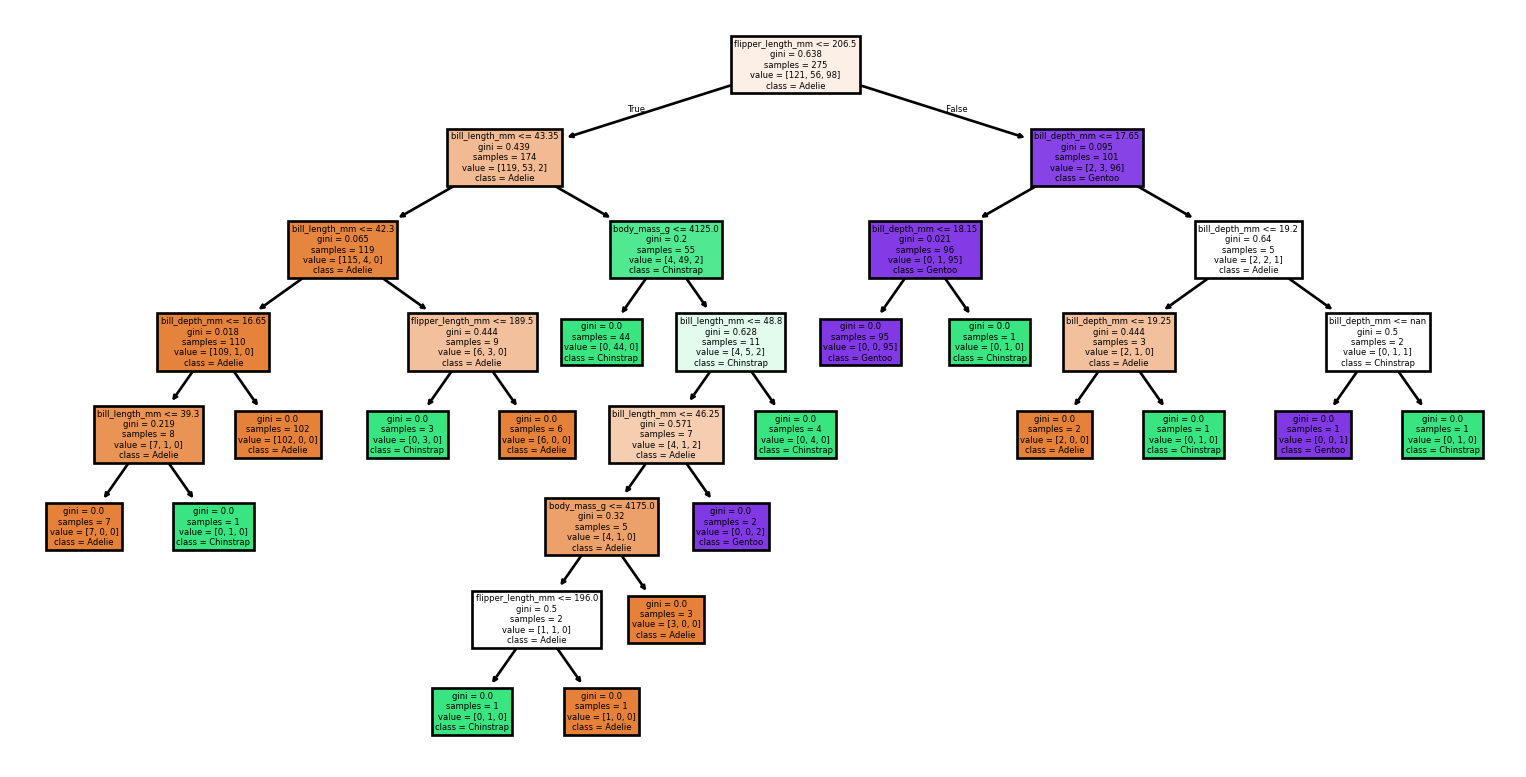
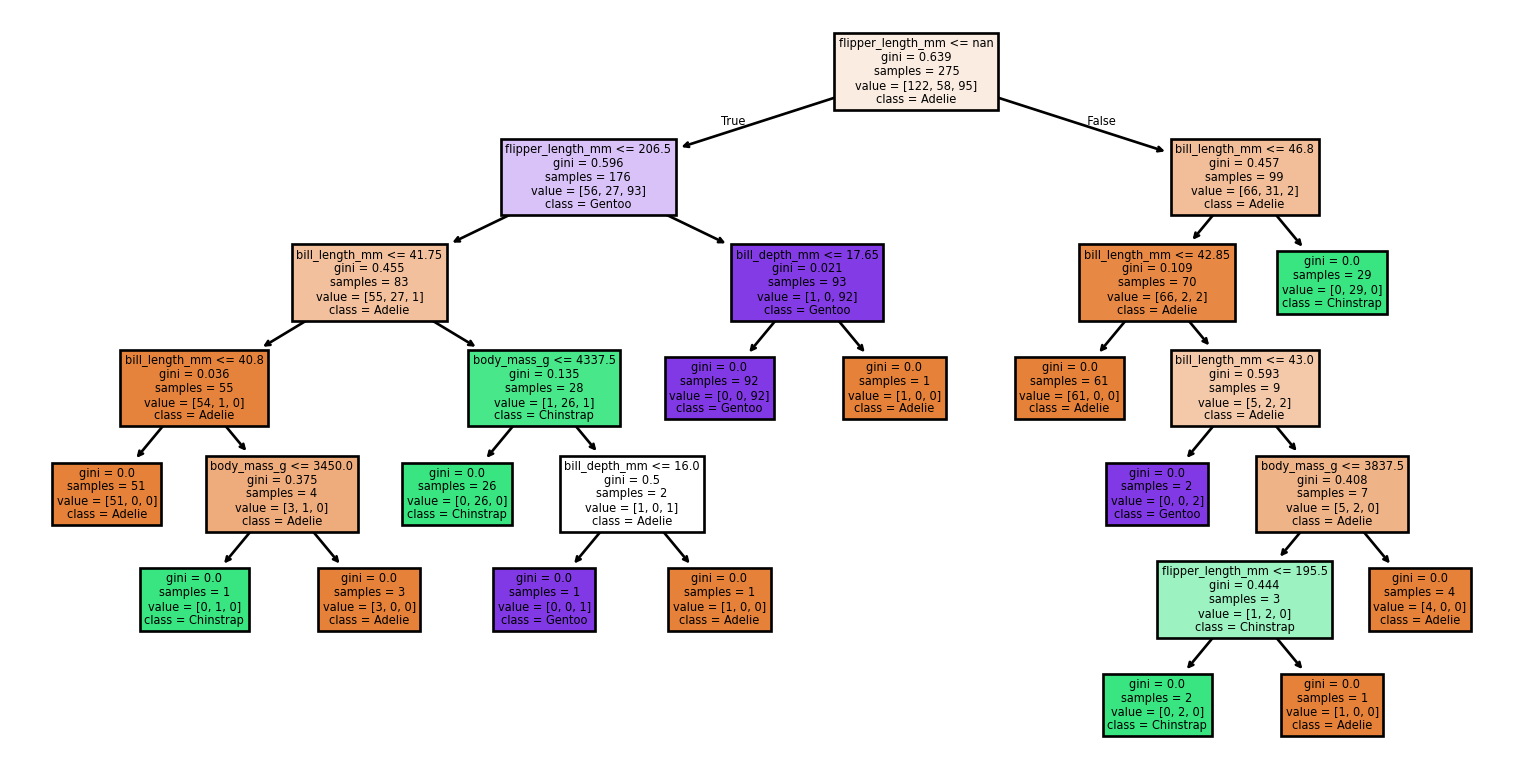
• Petits changements dans l’ensemble de données produisent des arbres très différents

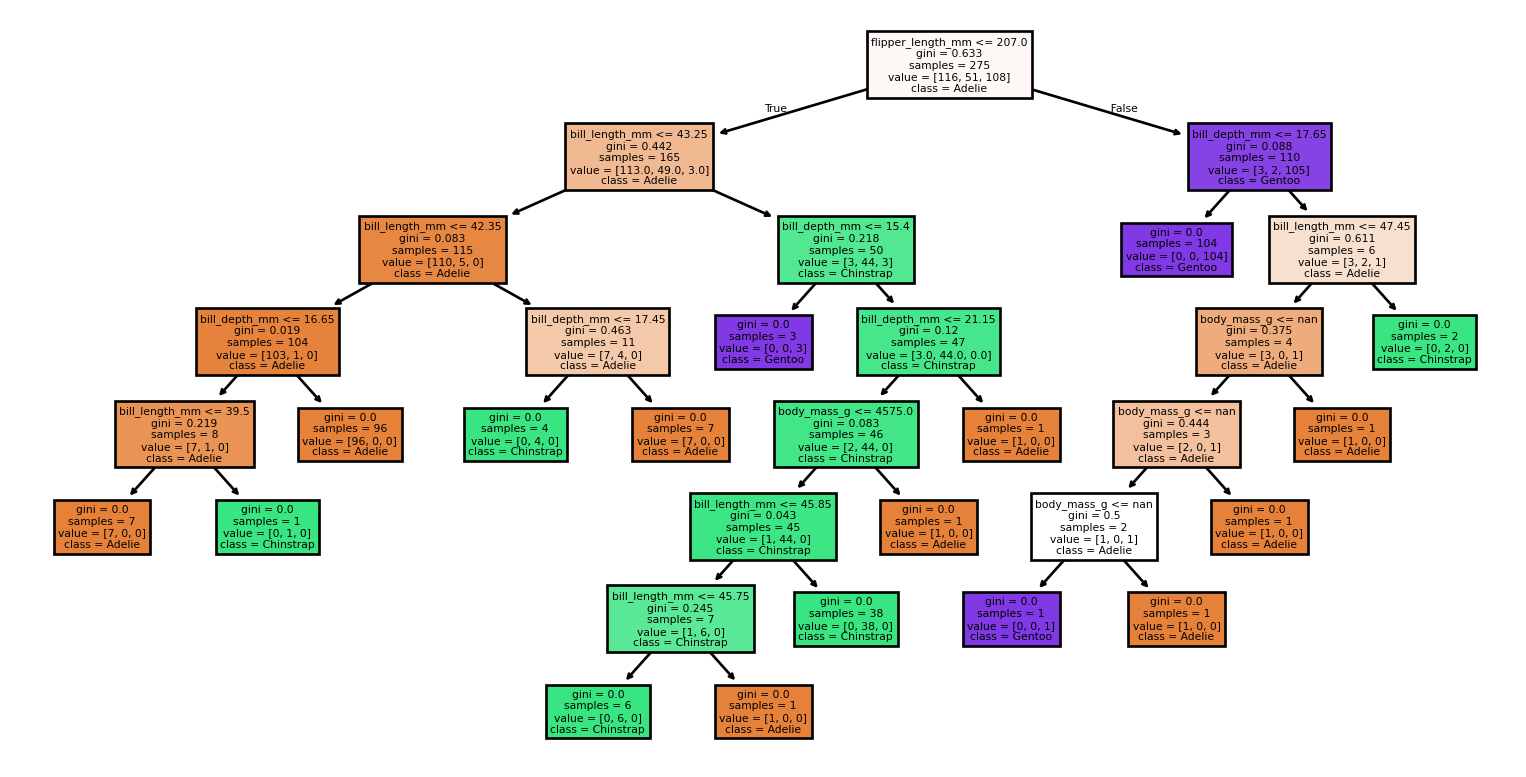
Arbres de grande taille

(Stiglic et al. 2012)

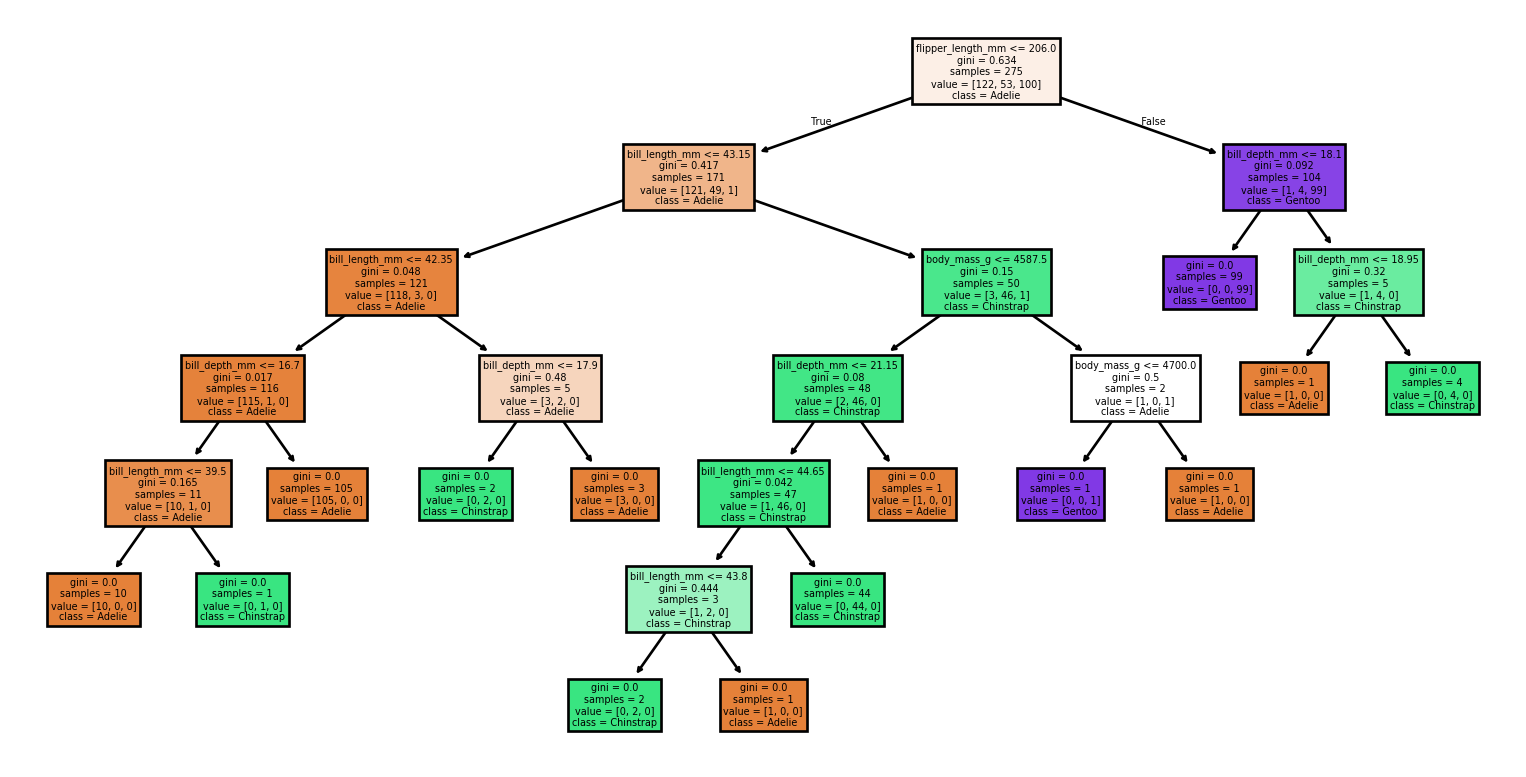
Petits changements dans l’ensemble de données

from sklearn import tree
from sklearn.metrics import classification_report, accuracy_score

# Chargement de l'ensemble de données

X, y = load_penguins(return_X_y = True)

target_names = ['Adelie','Chinstrap','Gentoo']

# Diviser l'ensemble de données en ensembles d'entraînement et de test

for seed in (4, 7, 90, 96, 99, 2):

  print(f'Seed: {seed}')

  # Créer de nouveaux ensembles d'entraînement et de test basés sur une graine aléatoire différente

  X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=seed)

  # Création d'un nouveau classificateur

  clf = tree.DecisionTreeClassifier(random_state=seed)

  # Entraînement

  clf.fit(X_train, y_train)

  # Faire des prédictions

  y_pred = clf.predict(X_test)

  # Tracé de l'arbre

  tree.plot_tree(clf, 
               feature_names = X.columns,
               class_names = target_names,
               filled = True)
  plt.show()

  # Évaluation du modèle

  accuracy = accuracy_score(y_test, y_pred)

  report = classification_report(y_test, y_pred, target_names=target_names)

  print(f'Accuracy: {accuracy:.2f}')
  print('Rapport de Classification:')
  print(report)

Petits changements dans l’ensemble de données

Seed: 4

Accuracy: 0.99
Rapport de Classification:
              precision    recall  f1-score   support

      Adelie       1.00      0.97      0.99        36
   Chinstrap       0.94      1.00      0.97        17
      Gentoo       1.00      1.00      1.00        16

    accuracy                           0.99        69
   macro avg       0.98      0.99      0.99        69
weighted avg       0.99      0.99      0.99        69

Seed: 7

Accuracy: 0.91
Rapport de Classification:
              precision    recall  f1-score   support

      Adelie       0.96      0.83      0.89        30
   Chinstrap       0.83      1.00      0.91        15
      Gentoo       0.92      0.96      0.94        24

    accuracy                           0.91        69
   macro avg       0.90      0.93      0.91        69
weighted avg       0.92      0.91      0.91        69

Seed: 90

Accuracy: 0.94
Rapport de Classification:
              precision    recall  f1-score   support

      Adelie       0.90      1.00      0.95        26
   Chinstrap       0.93      0.88      0.90        16
      Gentoo       1.00      0.93      0.96        27

    accuracy                           0.94        69
   macro avg       0.94      0.93      0.94        69
weighted avg       0.95      0.94      0.94        69

Seed: 96

Accuracy: 0.90
Rapport de Classification:
              precision    recall  f1-score   support

      Adelie       0.83      0.97      0.89        30
   Chinstrap       1.00      0.67      0.80        15
      Gentoo       0.96      0.96      0.96        24

    accuracy                           0.90        69
   macro avg       0.93      0.86      0.88        69
weighted avg       0.91      0.90      0.90        69

Seed: 99

Accuracy: 1.00
Rapport de Classification:
              precision    recall  f1-score   support

      Adelie       1.00      1.00      1.00        31
   Chinstrap       1.00      1.00      1.00        12
      Gentoo       1.00      1.00      1.00        26

    accuracy                           1.00        69
   macro avg       1.00      1.00      1.00        69
weighted avg       1.00      1.00      1.00        69

Seed: 2

Accuracy: 0.55
Rapport de Classification:
              precision    recall  f1-score   support

      Adelie       0.62      0.97      0.75        30
   Chinstrap       0.43      0.90      0.58        10
      Gentoo       0.00      0.00      0.00        29

    accuracy                           0.55        69
   macro avg       0.35      0.62      0.44        69
weighted avg       0.33      0.55      0.41        69

Résumé

• Le cours a passé en revue trois algorithmes d’apprentissage : k-plus proches voisins (KNN), arbres de décision et régression linéaire, et les a présentés via leur modèle, objectif et optimisation.
• Nous avons ensuite construit des arbres de décision, montré que les feuilles de régression retournaient la moyenne de l’échantillon, minimisé l’impureté pondérée \(J\), et analysé l’indice de Gini.
• Les frontières de décision ont été illustrées pour les modèles linéaires et non linéaires.

Prologue

Ressources

• Plot the decision surface of decision trees trained on the iris dataset de sklearn
• Decision trees by Jan Kirenz, HdM Stuttgart
• CS 320 Apr12-2021 (Part 2) - Decision Boundaries par Tyler Caraza-Harter, un instructeur à UW-Madison

References

Géron, Aurélien. 2019. Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow. 2nd éd. O’Reilly Media.

Geurts, Pierre, Alexandre Irrthum, et Louis Wehenkel. 2009. « Supervised learning with decision tree-based methods in computational and systems biology ». Molecular bioSystems 5 (12): 1593‑1605. https://doi.org/10.1039/b907946g.

Hyafil, Laurent, et Ronald L. Rivest. 1976. « Constructing Optimal Binary Decision Trees is NP-Complete ». Inf. Process. Lett. 5 (1): 15‑17. https://doi.org/10.1016/0020-0190(76)90095-8.

Russell, Stuart, et Peter Norvig. 2020. Artificial Intelligence: A Modern Approach. 4ᵉ éd. Pearson. http://aima.cs.berkeley.edu/.

Stiglic, Gregor, Simon Kocbek, Igor Pernek, et Peter Kokol. 2012. « Comprehensive decision tree models in bioinformatics ». Édité par Ahmed Moustafa. PLoS ONE 7 (3): e33812. https://doi.org/10.1371/journal.pone.0033812.

Prochain cours

• Régression linéaire

Marcel Turcotte

Marcel.Turcotte@uOttawa.ca

École de science informatique et de génie électrique (SIGE)

Université d’Ottawa