Régression logistique

CSI 4506 - automne 2025

Marcel Turcotte

Version: sept. 17, 2025 15h24

Préambule

Message du jour

Un podcast de 30 minutes où Garry Kasparov est rejoint par le scientifique cognitif Gary Marcus.

Garry Kasparov (né en 1963) est un grand maître d’échecs russe et ancien champion du monde, largement considéré comme l’un des plus grands joueurs de l’histoire. Il a occupé le premier rang mondial pendant près de deux décennies et est également connu pour ses matchs contre Deep Blue d’IBM ainsi que pour son activisme politique et ses écrits ultérieurs.

Gary Marcus (né en 1965) est un scientifique cognitif américain, auteur et entrepreneur. Il est connu pour ses critiques de l’apprentissage profond, ses travaux sur l’acquisition du langage et le développement cognitif, et pour avoir fondé plusieurs startups en intelligence artificielle.

Kasparov et Marcus s’accordent à dire que l’IA est un outil—ni intrinsèquement utopique ni dystopique—and que les véritables risques proviennent de la manière dont elle est utilisée et par qui. Marcus souligne que les systèmes d’IA actuels manquent encore de véritable compréhension; ils fonctionnent par reconnaissance de motifs sur de vastes ensembles de données, et non par la compréhension de règles ou de concepts, ce qui entraîne des problèmes d’alignement : les machines font fréquemment des erreurs ou agissent de manière imprévue. Une préoccupation majeure est la manière dont l’IA amplifie la tromperie politique, la surveillance et la manipulation de l’information—des outils prisés par les intérêts autocratiques ou oligarchiques. Du côté positif, ils soutiennent que nous ne sommes pas impuissants : les sociétés démocratiques ont encore des leviers—réglementation légale, action de masse, résistance, insistance sur la responsabilité—et pourraient encore orienter l’IA pour qu’elle profite à la démocratie plutôt que de la saper. Le chemin par défaut est dangereux, mais avec une volonté politique, il n’est pas nécessaire de glisser irréversiblement vers le techno-fascisme. (Résumé généré par ChatGPT 5 le 2025-09-16)

AI and the Rise of Techno-Fascism in the United States par Gary Kasparov, The Atlantic, 2025-09-05. (31m 13s)

Objectifs d’apprentissage

• Différencier entre les paradigmes de classification binaire et de classification multi-classes.
• Décrire une méthodologie pour convertir des problèmes de classification multi-classes en tâches de classification binaire.
• Implémenter un algorithme de régression logistique, en se concentrant sur son application aux problèmes de classification.

Tâches de classification

Définitions

• La classification binaire est une tâche d’apprentissage supervisé dont l’objectif est de catégoriser des instances (exemples) en deux classes distinctes.

• Une tâche de classification multi-classes est un type de problème d’apprentissage supervisé où l’objectif est de catégoriser des instances en trois classes distinctes ou plus.

• Un exemple de tâche de classification binaire est la prédiction du statut de maladie à l’aide de données génomiques (Wu et al. 2018).

• Les chercheurs cherchent souvent à classifier avec précision le type, le sous-type ou le stade d’un cancer en utilisant des données d’expression génique. Par exemple, dans le Pan-Cancer Atlas, des cancers spécifiques tels que le cancer du sein (BRCA), l’adénocarcinome du côlon (COAD), l’adénocarcinome pulmonaire (LUAD), le cancer de l’ovaire (OV) et le cancer de la thyroïde (THCA) peuvent être différenciés sur la base de leurs profils d’expression génique uniques (Alharbi et Vakanski 2023).

Attention : La classification multi-classes ne doit pas être confondue avec la classification multi-étiquettes, qui permet à une instance d’être associée à plusieurs classes. Les algorithmes conçus pour traiter ces tâches diffèrent de manière significative.

Classification binaire

• Certains algorithmes de machine learning sont spécifiquement conçus pour résoudre des problèmes de classification binaire.
  • La régression logistique et les machines à vecteurs de support (SVM) en sont des exemples.

Plus tard dans la présentation, assurez-vous de comprendre pourquoi la régression logistique est spécifiquement conçue pour résoudre les problèmes de classification binaire.

Classification multi-classes

• Tout problème de classification multi-classes peut être transformé en un problème de classification binaire.
• Un-contre-tous (One-vs-All – OvA)
  • Un classificateur binaire distinct est entraîné pour chaque classe.
  • Pour chaque classificateur, une classe est traitée comme la classe positive, et toutes les autres classes sont traitées comme les classes négatives.
  • L’attribution finale d’une étiquette de classe est effectuée en fonction du classificateur qui produit le score de confiance le plus élevé pour une entrée donnée.

Scikit-learn propose OneVsRestClassifier, un utilitaire conçu pour étendre les classificateurs binaires aux tâches de classification multi-classes via la stratégie One-vs-Rest.

Un exemple complet sera présenté à la fin du cours.

Régression logistique

Données et problème

• Jeu de données : Palmer Penguins
• Tâche : Classification binaire pour distinguer les manchots Gentoo des espèces non-Gentoo
• Attribut : Longueur des nageoires

Histogramme

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

try:
    from palmerpenguins import load_penguins
except ImportError:
    ! pip install palmerpenguins
    from palmerpenguins import load_penguins

# Charger le jeu de données Palmer Penguins
df = load_penguins()

# Ne garder que 'flipper_length_mm' et 'species'
df = df[['flipper_length_mm', 'species']]

# Supprimer les lignes avec des valeurs manquantes (NaNs)
df.dropna(inplace=True)

# Créer une étiquette binaire : 1 si Gentoo, 0 sinon
df['is_gentoo'] = (df['species'] == 'Gentoo').astype(int)

# Séparer les attributs (X) et les étiquettes (y)
X = df[['flipper_length_mm']]
y = df['is_gentoo']

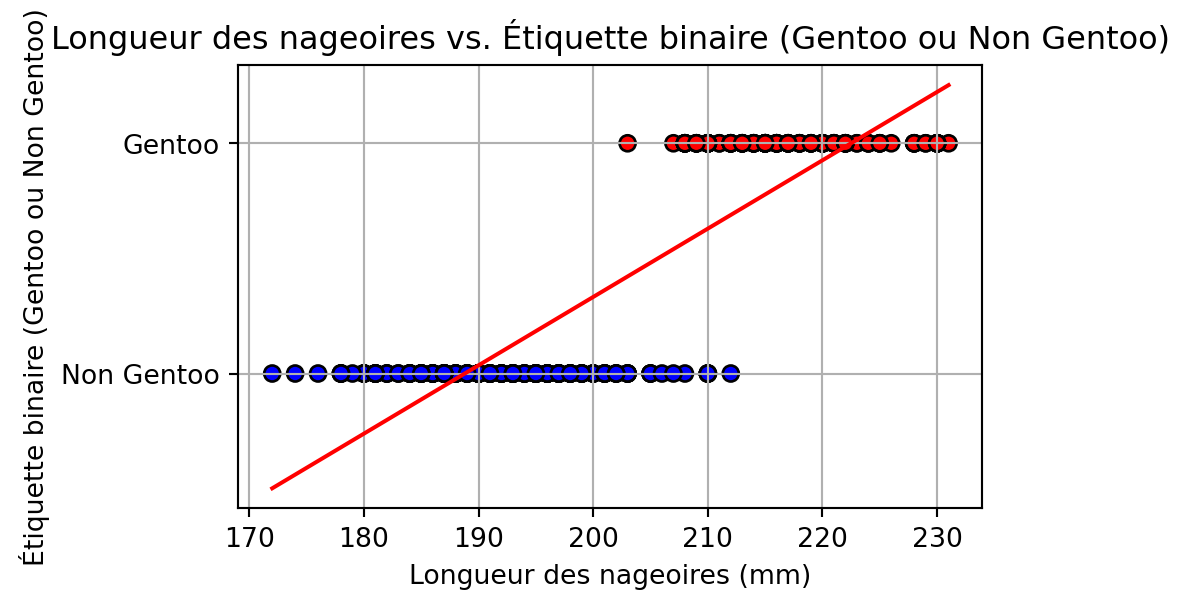
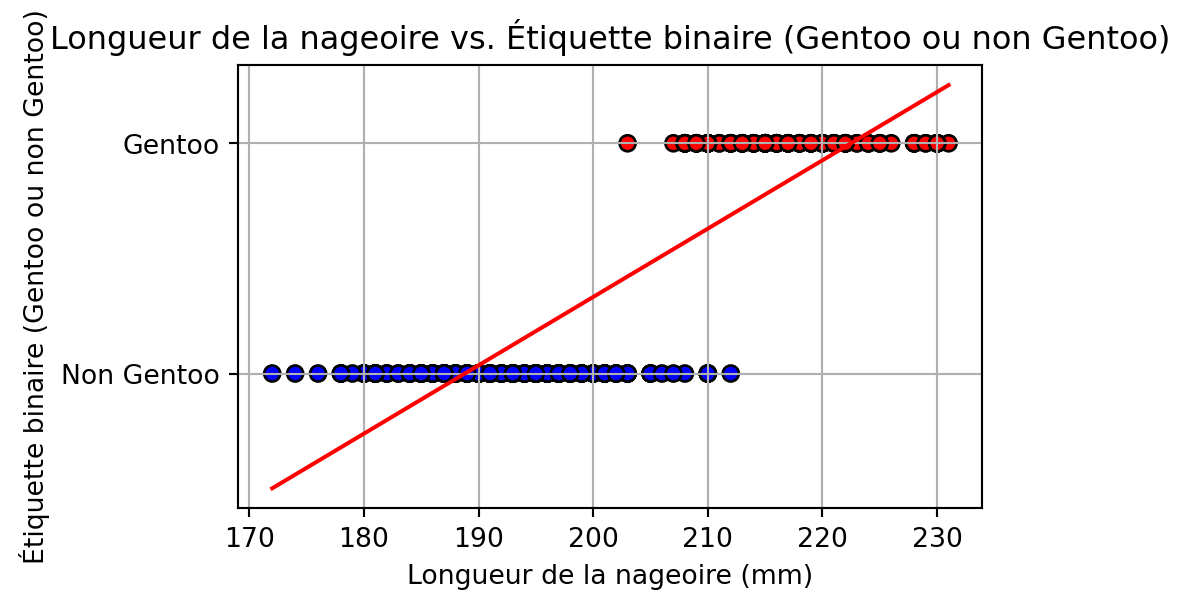
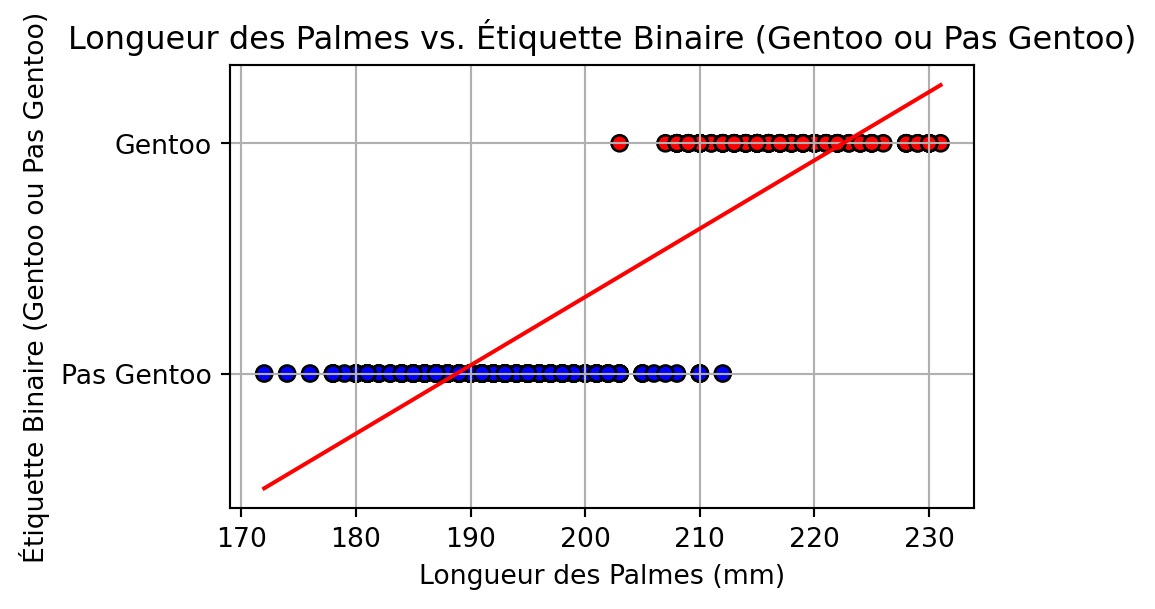
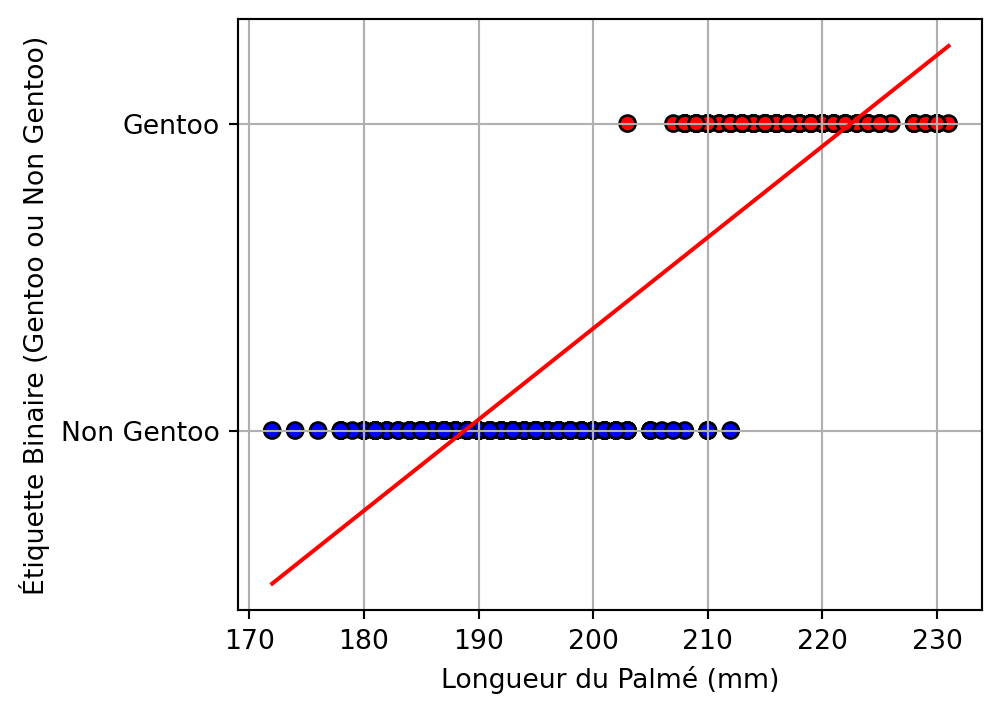
# Tracer la distribution des longueurs de nageoires par étiquette d'espèce binaire
plt.figure(figsize=(10, 6))
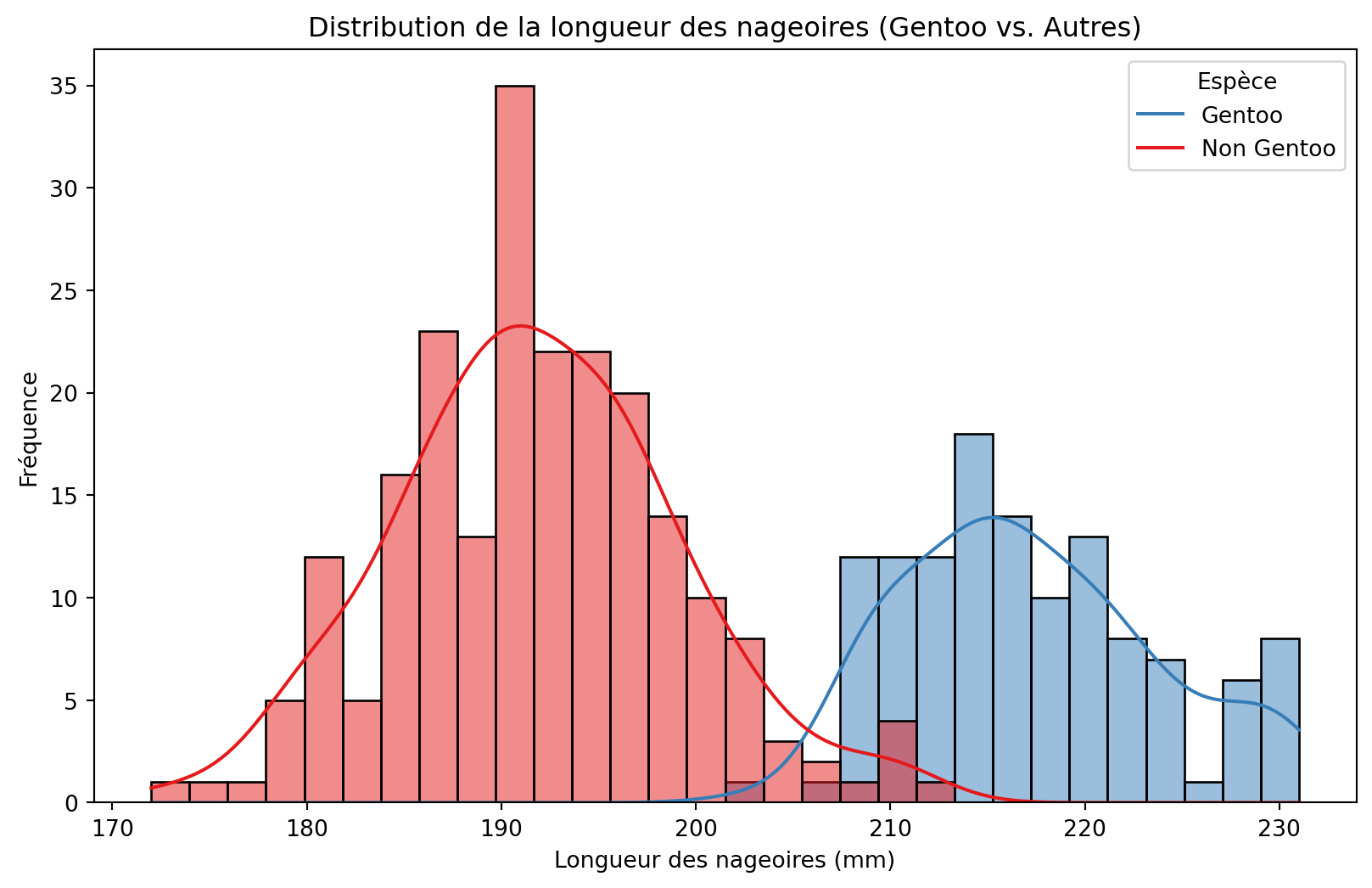
sns.histplot(data=df, x='flipper_length_mm', hue='is_gentoo', kde=True, bins=30, palette='Set1')
plt.title('Distribution de la longueur des nageoires (Gentoo vs. Autres)')
plt.xlabel('Longueur des nageoires (mm)')
plt.ylabel('Fréquence')
plt.legend(title='Espèce', labels=['Gentoo', 'Non Gentoo'])
plt.show()

Régression logistique (Logit)

• Malgré son nom, la régression logistique sert de technique de classification plutôt que de méthode de régression.

• Les étiquettes en régression logistique sont des valeurs binaires, notées \(y_i \in \{0,1\}\), ce qui en fait une tâche de classification binaire.

• L’objectif principal de la régression logistique est de déterminer la probabilité qu’un exemple donné \(x_i\) appartienne à la classe positive, c’est-à-dire \(y_i = 1\).

La représentation des deux classes, négative et positive, par les valeurs 0 et 1 respectivement, n’est pas arbitraire. Ce choix est intrinsèquement lié à notre objectif de déterminer la probabilité qu’une instance \(x_i\) appartienne à la classe positive.

Bien que cet algorithme d’apprentissage puisse sembler peu remarquable au départ, il est essentiel de continuer à s’y intéresser, car la régression logistique s’avérera plus tard cruciale dans la discussion sur les réseaux de neurones artificiels.

Modèle

• Cas Général : \(P(y = k | x, \theta)\), où \(k\) est une étiquette de classe.
• Cas Binaire : \(y \in \{0,1\}\)
  • Prédire \(P(y = 1 | x, \theta)\)

Visualiser nos données

# Diagramme de dispersion de la longueur des nageoires vs. étiquette binaire (Gentoo ou Non Gentoo)
plt.figure(figsize=(10, 6))

# Points étiquetés comme Gentoo (is_gentoo = 1)
plt.scatter(
    df.loc[df['is_gentoo'] == 1, 'flipper_length_mm'],
    df.loc[df['is_gentoo'] == 1, 'is_gentoo'],
    color='blue',
    label='Gentoo'
)

# Points étiquetés comme Non Gentoo (is_gentoo = 0)
plt.scatter(
    df.loc[df['is_gentoo'] == 0, 'flipper_length_mm'],
    df.loc[df['is_gentoo'] == 0, 'is_gentoo'],
    color='red',
    label='Non Gentoo'
)

plt.title('Longueur des Nageoires vs. Indicateur Gentoo')
plt.xlabel('Longueur des Nageoires (mm)')
plt.ylabel('Étiquette Binaire (1 = Gentoo, 0 = Non Gentoo)')
plt.legend(loc='best')
plt.grid(True)
plt.show()

Intuition

Ajuster une régression linéaire n’est pas la solution, mais \(\ldots\)

from sklearn.linear_model import LinearRegression
import pandas as pd

lin_reg = LinearRegression()
lin_reg.fit(X, y)

X_new = pd.DataFrame([X.min(), X.max()], columns=X.columns)

y_pred = lin_reg.predict(X_new)

# Tracer le nuage de points
plt.figure(figsize=(5, 3))
plt.scatter(X, y, c=y, cmap='bwr', edgecolor='k')
plt.plot(X_new, y_pred, "r-")
plt.xlabel('Longueur des nageoires (mm)')
plt.ylabel('Étiquette binaire (Gentoo ou Non Gentoo)')
plt.title('Longueur des nageoires vs. Étiquette binaire (Gentoo ou Non Gentoo)')
plt.yticks([0, 1], ['Non Gentoo', 'Gentoo'])
plt.grid(True)
plt.show()

Intuition (suite)

• Une haute flipper_length_mm aboutit généralement à une sortie du modèle proche de 1.

• Inversement, une faible flipper_length_mm produit généralement une sortie du modèle proche de 0.

• Notamment, les sorties du modèle ne sont pas confinées à l’intervalle [0, 1] et peuvent occasionnellement être inférieures à 0 ou dépasser 1.

Sure, here’s the translation of the selected text into French:

Intuition (suite)

• Pour un seul attribut, la frontière de décision est un point spécifique.
• Dans ce cas, la frontière de décision est d’environ 205.

Intuition (suite)

• À mesure que longueur_nageoire_mm augmente de 205 à 230, la confiance dans la classification de l’exemple en tant que Gentoo augmente.
• Inversement, à mesure que longueur_nageoire_mm diminue de 205 à 170, la confiance dans la classification de l’exemple en tant que non-Gentoo augmente.

Intuition (suite)

• Pour les valeurs proches de la frontière de décision, 205, certains exemples sont classés comme Gentoo tandis que d’autres ne le sont pas, ce qui conduit à une incertitude de classification comparable à un lancer de pièce (probabilité de 0,5).

Fonction logistique

Fonction logistique

La fonction logistique standard transforme une entrée à valeur réelle de \(\mathbb{R}\) en l’intervalle ouvert \((0,1).\) La fonction est définie comme suit :

\[ \sigma(t) = \frac{1}{1+e^{-t}} \]

# Fonction Sigmoïde
def sigmoid(t):
    return 1 / (1 + np.exp(-t))

# Générer des valeurs de t
t = np.linspace(-6, 6, 1000)

# Calculer les valeurs de y pour la fonction sigmoïde
sigma = sigmoid(t)

# Créer une figure
fig, ax = plt.subplots()
ax.plot(t, sigma, color='blue', linewidth=2)  # Garder la courbe opaque

# Tracer l'axe vertical à x = 0
ax.axvline(x=0, color='black', linewidth=1)

# Ajouter des étiquettes sur l'axe vertical
ax.set_yticks([0, 0.5, 1.0])

# Ajouter des étiquettes aux axes
ax.set_xlabel('t')
ax.set_ylabel(r'$\sigma(t)$')

plt.grid(True)
plt.show()

• Lorsque la variable d’entrée \(t\) est égale à 0, la sortie de la fonction logistique est de 0,5.
  • En effet, \(e^{-t} = {e^0} = 1\) et donc \(\frac{1}{1+e^{-t}} = \frac{1}{1+1}= \frac{1}{2}.\)
• À mesure que \(t\) augmente, la valeur de sortie se rapproche de 1.
  • Lorsque \(t \to \infty\), \(e^{-t} \to 0\).
• Inversement, à mesure que \(t\) devient plus négatif, la valeur de sortie se rapproche de 0.
  • Lorsque \(t \to -\infty\), \(e^{-t} \to \infty\) (les deux signes négatifs s’annulent).
• La fonction logistique standard est également couramment appelée fonction sigmoïde.

Régression logistique (intuition)

• Lorsque la distance à la frontière de décision est zéro, l’incertitude est élevée, rendant une probabilité de 0,5 appropriée.
• À mesure que nous nous éloignons de la frontière de décision, la confiance augmente, justifiant des probabilités plus hautes ou plus basses en conséquence.

Fonction logistique

Une courbe en forme de S, telle que la fonction logistique standard (également appelée sigmoïde), est qualifiée de fonction d’écrasement (squashing function) car elle transforme un large domaine d’entrée en une plage de sortie restreinte.

\[ \sigma(t) = \frac{1}{1+e^{-t}} \]

Régression Logistique (Logit)

• De manière analogue à la régression linéaire, la régression logistique calcule une somme pondérée des attributs d’entrée, exprimée comme suit : \[ \theta_0 + \theta_1 x_i^{(1)} + \theta_2 x_i^{(2)} + \ldots + \theta_D x_i^{(D)} \]

• Cependant, l’utilisation de la fonction sigmoïde limite sa sortie à l’intervalle \((0,1)\) : \[ \sigma(\theta_0 + \theta_1 x_i^{(1)} + \theta_2 x_i^{(2)} + \ldots + \theta_D x_i^{(D)}) \]

Notation

• Equation de la régression logistique: \[ \sigma(\theta_0 + \theta_1 x_i^{(1)} + \theta_2 x_i^{(2)} + \ldots + \theta_D x_i^{(D)}) \]

• Multipling \(\theta_0\) (intercept/bias) by 1: \[ \sigma(\theta_0 \times 1 + \theta_1 x_i^{(1)} + \theta_2 x_i^{(2)} + \ldots + \theta_D x_i^{(D)}) \]

• Multipling \(\theta_0\) by \(x_i^{(0)} = 1\): \[ \sigma(\theta_0 x_i^{(0)} + \theta_1 x_i^{(1)} + \theta_2 x_i^{(2)} + \ldots + \theta_D x_i^{(D)}) \]

Régression logistique

Le modèle de Régression Logistique, sous sa forme vectorisée, est défini comme suit : \[ h_\theta(x_i) = \sigma(\theta x_i) = \frac{1}{1+e^{- \theta x_i}} \]

Une caractéristique supplémentaire, \(x_i^{(0)} = 1\), a été ajoutée à \(x_i\), et \(\theta_0\) est le terme d’interception/biais.

Régression logistique (deux attributs)

\[ h_\theta(x_i) = \sigma(\theta x_i) \]

• En régression logistique, la probabilité de classer correctement un exemple augmente à mesure que sa distance par rapport à la frontière de décision augmente.
• Ce principe est valable pour les classes positives et négatives.
• Un exemple situé sur la frontière de décision a une probabilité de 50% d’appartenir à l’une ou l’autre des classes.

Régression logistique

• Le modèle de Régression Logistique, sous sa forme vectorisée, est défini comme suit : \[ h_\theta(x_i) = \sigma(\theta x_i) = \frac{1}{1+e^{- \theta x_i}} \]

• Les prédictions sont faites comme suit :

  • \(y_i = 0\), si \(h_\theta(x_i) < 0.5\)
  • \(y_i = 1\), si \(h_\theta(x_i) \geq 0.5\)

• Les valeurs de \(\theta\) sont apprises en utilisant la descente de gradient.

“StatQuest décompose les méthodes complexes de statistiques et d’apprentissage automatique en petites sections faciles à comprendre. StatQuest ne simplifie pas excessivement le matériel ; au contraire, il vous renforce pour que vous soyez plus intelligent et ayez une meilleure compréhension des statistiques et de l’apprentissage automatique.” C’est souvent un bon point de départ pour acquérir l’intuition nécessaire à la compréhension des concepts statistiques et d’apprentissage automatique.

Attribution : StatQuest: Logistic Regression par Josh Starmer.

Chiffres manuscrits

1989 Yann LeCun

Reconnaissance de chiffres manuscrits

Objectifs :

• Développer un modèle de régression logistique pour la reconnaissance de chiffres manuscrits.

• Visualiser les informations et les motifs acquis par le modèle.

Nous utilisons les jeux de données UCI ML de chiffres manuscrits.

Chiffres manuscrits

Chargement du jeu de données

from sklearn.datasets import load_digits

digits = load_digits()

Quel est le type de digits.data

type(digits.data)

numpy.ndarray

Développement d’un modèle de régression logistique pour la reconnaissance des chiffres manuscrits de ce jeux de données de l’UCI ML.

Chiffres manuscrits

Combien d’exemples (N) et combien d’attributs (D)?

digits.data.shape

(1797, 64)

Définition des valeurs de N et D

N, D = digits.data.shape

target a-t-il le même nombre d’entrées (exemples) que data ?

digits.target.shape

(1797,)

Chiffres manuscrits

Quelles sont la largeur et la hauteur de ces images ?

digits.images.shape

(1797, 8, 8)

Définition des valeurs de width et height

_, width, height = digits.images.shape

Chiffres manuscrits

Définition des valeurs de X et y

X = digits.data
y = digits.target

Chiffres manuscrits

X[0] est un vecteur de taille width * height = D (\(8 \times 8 = 64\)).

X[0]

array([ 0.,  0.,  5., 13.,  9.,  1.,  0.,  0.,  0.,  0., 13., 15., 10.,
       15.,  5.,  0.,  0.,  3., 15.,  2.,  0., 11.,  8.,  0.,  0.,  4.,
       12.,  0.,  0.,  8.,  8.,  0.,  0.,  5.,  8.,  0.,  0.,  9.,  8.,
        0.,  0.,  4., 11.,  0.,  1., 12.,  7.,  0.,  0.,  2., 14.,  5.,
       10., 12.,  0.,  0.,  0.,  0.,  6., 13., 10.,  0.,  0.,  0.])

Il correspond à une image de \(8 \times 8 = 64\).

X[0].reshape(width, height)

array([[ 0.,  0.,  5., 13.,  9.,  1.,  0.,  0.],
       [ 0.,  0., 13., 15., 10., 15.,  5.,  0.],
       [ 0.,  3., 15.,  2.,  0., 11.,  8.,  0.],
       [ 0.,  4., 12.,  0.,  0.,  8.,  8.,  0.],
       [ 0.,  5.,  8.,  0.,  0.,  9.,  8.,  0.],
       [ 0.,  4., 11.,  0.,  1., 12.,  7.,  0.],
       [ 0.,  2., 14.,  5., 10., 12.,  0.,  0.],
       [ 0.,  0.,  6., 13., 10.,  0.,  0.,  0.]])

Chiffres manuscrits

Afficher les n=5 premiers exemples.

import matplotlib.pyplot as plt

plt.figure(figsize=(10,2))
n = 5

for index, (image, label) in enumerate(zip(X[0:n], y[0:n])):
    plt.subplot(1, n, index + 1)
    plt.imshow(np.reshape(image, (width,width)), cmap=plt.cm.gray)
    plt.title(f'y = {label}')

Les valeurs d’intensité proches de 0 sont représentées en noir, tandis que les valeurs élevées sont représentées en blanc.

Utiliser cmap=plt.cm.binary afin d’inverser les images (intensité proches de 0 en blanc, valeurs élevées en noir).

Chiffres manuscrits

import matplotlib.pyplot as plt

plt.figure(figsize=(10,2))
n = 5

for index, (image, label) in enumerate(zip(X[0:n], y[0:n])):
    plt.subplot(1, n, index + 1)
    plt.imshow(np.reshape(image, (width,width)), cmap=plt.cm.gray)
    plt.title(f'y = {label}')

• Dans notre ensemble de données, chaque \(x_i\) est un vecteur d’attributs de taille \(D = 64\).

• Ce vecteur est formé en concaténant les lignes d’une image de \(8 \times 8\).

• La fonction reshape est utilisée pour convertir ce vecteur de 64 dimensions en son format original d’image \(8 \times 8\).

Chiffres manuscrits

• Nous allons entraîner 10 classificateurs, chacun correspondant à un chiffre spécifique dans une approche Un-contre-Tous (OvA).

• Chaque classificateur déterminera les valeurs optimales des \(\theta_j\) (associées aux attributs pixels), lui permettant de distinguer un chiffre de tous les autres.

Chiffres manuscrits

Préparation de notre expérience en apprentissage automatique

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.1, random_state=42)

Chiffres manuscrits

Les algorithmes d’optimisation fonctionnent généralement mieux lorsque les attributs ont des plages de valeurs similaires.

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

Certains classificateurs présentent des performances sous-optimales lorsqu’il existe des variations significatives dans les échelles des attributs. Ce problème est particulièrement accentué dans les classificateurs qui utilisent la descente de gradient pour l’optimisation des paramètres, car ils peuvent être affectés négativement par les écarts d’échelle des attributs. Par conséquent, la standardisation des attributs est une pratique largement adoptée pour atténuer ce problème.

StandardScaler est une approche couramment utilisée. Pour un attribut donné, les valeurs sont transformées comme suit :

\[ z = \frac{(x - \mu)}{\sigma} \]

où \(\mu\) est la moyenne de toutes les valeurs pour cet attribut dans les données d’entraînement, et \(\sigma\) l’écart type correspondant.

Appeler fit oblige le scaler à apprendre la moyenne et l’écart type de chaque attribut. Appeler transform applique la transformation sur le jeu de données désigné. Enfin, appeler fit_transform combine les deux étapes.

Ce serait une erreur d’appliquer fit ou fit_transform sur l’ensemble du jeu de données, une erreur appelée fuite de données (data leakage). Les informations du jeu de test influenceraient la moyenne et l’écart type appris par le scaler. Les données d’entraînement seraient transformées en utilisant des informations biaisées par le jeu de test. Le modèle apprendrait à partir de données d’entraînement mises à l’échelle en utilisant des informations biaisées par le jeu de test. Le jeu de test ne serait plus indépendant.

Il est primordial de mettre à l’échelle les données de test. Le modèle a été entraîné sur des données mises à l’échelle, ici avec des valeurs moyennes centrées à zéro et un écart type de 1. Les données originales étaient probablement sur une échelle très différente. Imaginez un attribut représentant la température en Celsius, avec des valeurs de -40 à 40. Un autre attribut, représentant une note, avec des valeurs de 0 à 100. Le modèle produirait des résultats incohérents sur de telles données. Les données de test doivent être mises à l’échelle en utilisant la moyenne et l’écart type des données d’entraînement, qui représentent le cadre de référence pour son entraînement.

1. Équité dans l’évaluation (pas de tricherie) : Si vous utilisez les données de test pour calculer la moyenne et la variance, vous jetez un coup d’œil aux réponses. Même si c’est “juste” une moyenne et un écart type, cela reste des informations provenant du jeu de test. Cela viole le principe selon lequel les données de test doivent rester complètement invisibles jusqu’à l’évaluation.

2. Cohérence de la distribution : Le modèle a été entraîné en supposant que les attributs sont centrés et mises à l’échelle en utilisant la distribution d’entraînement. Si vous mettez à l’échelle les données de test différemment (par exemple, avec sa propre moyenne/écart type), alors les nombres que le modèle voit ne correspondent plus à la distribution sur laquelle il a été entraîné. C’est comme donner au modèle des entrées dans une “nouvelle langue.”

3. Perspective de déploiement : Dans les applications réelles, vous n’aurez que la distribution d’entraînement pour calculer les paramètres de mise à l’échelle. Lorsque le modèle est déployé, vous ne pouvez pas arrêter le temps pour recalculer la mise à l’échelle chaque fois que de nouvelles données arrivent — vous devez appliquer la transformation fixe apprise à partir des données d’entraînement.

“Le scaler fait partie du modèle.” Tout comme les poids dans la régression logistique, la moyenne et la variance du StandardScaler sont apprises à partir du jeu d’entraînement. Une fois apprises, elles deviennent des paramètres fixes de votre pipeline de pré-traitement.

“Entraînement vs. examen.” Les données d’entraînement sont votre matériel d’étude ; les données de test sont l’examen. Vous ne pouvez pas regarder les questions de l’examen pour préparer vos notes (utiliser les données de test pour la mise à l’échelle), et vous ne pouvez pas changer le système de notation de l’examen à mi-chemin (mise à l’échelle des données de test séparément). Vous devez vous préparer avec vos notes d’étude (distribution d’entraînement) et ensuite passer l’examen dans le même cadre.

“La même règle pour tout le monde.” La mise à l’échelle est comme utiliser une règle pour mesurer des hauteurs. Vous calibrez la règle une fois avec les données d’entraînement. Si vous utilisiez une règle différente pour les données de test, les nombres ne seraient plus comparables.

Discussion : importance d’appliquer fit_transform uniquement à X_train

Chiffres manuscrits

from sklearn.linear_model import LogisticRegression
from sklearn.multiclass import OneVsRestClassifier

clf = OneVsRestClassifier(LogisticRegression())
clf = clf.fit(X_train, y_train)

Chaque régression logistique trouve un hyperplan dans un espace à 64 dimensions qui sépare les données en deux classes.

Demander au classificateur de résoudre une tâche multiclasses en utilisant un-contre-tous (OvR), aussi connu sous le nom d’OvA. Les classificateurs dans sklearn ont un support multiclasse intégré.

Chiffres manuscrits

Application du classificateur à notre ensemble de test

from sklearn.metrics import classification_report

y_pred = clf.predict(X_test)

print(classification_report(y_test, y_pred))

              precision    recall  f1-score   support

           0       1.00      1.00      1.00        17
           1       1.00      1.00      1.00        11
           2       1.00      1.00      1.00        17
           3       1.00      0.94      0.97        17
           4       1.00      1.00      1.00        25
           5       0.96      1.00      0.98        22
           6       1.00      1.00      1.00        19
           7       1.00      0.95      0.97        19
           8       0.80      1.00      0.89         8
           9       0.96      0.92      0.94        25

    accuracy                           0.98       180
   macro avg       0.97      0.98      0.97       180
weighted avg       0.98      0.98      0.98       180

Visualisation

Combien de classes ?

clf.classes_

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

Les coefficients et les intercepts sont dans des tableaux distincts.

(clf.estimators_[0].coef_.shape, clf.estimators_[0].intercept_.shape)

((1, 64), (1,))

Les intercepts sont \(\theta_0\), tandis que les coefficients sont \(\theta_j, j \in [1,64]\).

Adapté de MNIST digits classification using Logistic regression in Scikit-Learn, consulté le 2024-09-23.

Visualisation

clf.estimators_[0].coef_[0].round(2).reshape(width, height)

array([[ 0.  , -0.25,  0.04,  0.21,  0.02, -0.58, -0.36, -0.05],
       [ 0.  , -0.39,  0.04,  0.43,  0.53,  0.72, -0.03, -0.12],
       [-0.03,  0.19,  0.28, -0.04, -0.94,  0.84, -0.01, -0.06],
       [-0.04,  0.27,  0.26, -0.57, -1.75,  0.24,  0.07, -0.03],
       [ 0.  ,  0.32,  0.57, -0.58, -1.62, -0.15,  0.17,  0.  ],
       [-0.08, -0.13,  0.92, -0.85, -0.83, -0.01,  0.22, -0.  ],
       [-0.04, -0.36,  0.61, -0.14,  0.28,  0.01, -0.37, -0.41],
       [ 0.01, -0.31, -0.31,  0.54, -0.32, -0.18, -0.32, -0.21]])

Visualisation

coef = clf.estimators_[0].coef_
plt.imshow(coef[0].reshape(width,height))

Visualisation

plt.figure(figsize=(10,5))

for index in range(len(clf.classes_)):
    plt.subplot(2, 5, index + 1)
    plt.title(f'y = {clf.classes_[index]}')
    # plt.imshow(clf.coef_[index].reshape(width,width), 
    plt.imshow(clf.estimators_[index].coef_.reshape(width,width), 
               cmap=plt.cm.RdBu)

Chaque LogisticRegression apprend D=64 paramètres \(\theta_j\).

Dans les images ci-dessus, les pixels rouges correspondent à des coefficients négatifs, tandis que les pixels bleus correspondent à des coefficients positifs.

Pour le premier classificateur, qui prédit le chiffre ‘0’, le modèle attribue des poids négatifs aux pixels de haute intensité au centre de l’image et des poids positifs aux pixels de haute intensité dans la région ovale entourant le centre.

Visualisation

plt.figure(figsize=(10,5))

for index in range(len(clf.classes_)):
    plt.subplot(2, 5, index + 1)
    plt.title(f'y = {clf.classes_[index]}')
    # plt.imshow(clf.coef_[index].reshape(width,width), 
    plt.imshow(clf.estimators_[index].coef_.reshape(width,width), 
               cmap=plt.cm.RdBu,
               interpolation='bilinear')

Attribution: Machine Learning and Logistic Regression, IBM Technology, 2024-07-19.

Prologue

Références

Alharbi, Fadi, et Aleksandar Vakanski. 2023. « Machine Learning Methods for Cancer Classification Using Gene Expression Data: A Review ». Bioengineering 10 (2): 173. https://doi.org/10.3390/bioengineering10020173.

Russell, Stuart, et Peter Norvig. 2020. Artificial Intelligence: A Modern Approach. 4ᵉ éd. Pearson. http://aima.cs.berkeley.edu/.

Wu, Qianfan, Adel Boueiz, Alican Bozkurt, Arya Masoomi, Allan Wang, Dawn L DeMeo, Scott T Weiss, et Weiliang Qiu. 2018. « Deep Learning Methods for Predicting Disease Status Using Genomic Data ». Journal of biometrics & biostatistics 9 (5).

Ressource

• Logistic Regression 3-class Classifier par sklearn

Prochain cours

• Évaluation croisée et mesures de performance

Annexe

Un-contre-Tous (complet)

from sklearn.model_selection import train_test_split
from sklearn.preprocessing import label_binarize

# Load the Iris dataset
iris = load_iris()
X, y = iris.data, iris.target

# Binarize the output
y_bin = label_binarize(y, classes=[0, 1, 2])

# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y_bin, test_size=0.2, random_state=42)

Un-contre-Tous (complet)

# Train a One-vs-All classifier for each class

classifiers = []
for i in range(3):
    clf = LogisticRegression()
    clf.fit(X_train, y_train[:, i])
    classifiers.append(clf)

Chaque régression logistique trouve un hyperplan dans un espace à 4 dimensions qui sépare les données en deux classes.

Un-contre-Tous (complet)

# Predict on a new sample
new_sample = X_test[0].reshape(1, -1)

confidences = [clf.decision_function(new_sample) for clf in classifiers]

# Final assignment
final_class = np.argmax(confidences)

# Printing the result
print(f"Final class assigned: {iris.target_names[final_class]}")
print(f"True class: {iris.target_names[np.argmax(y_test[0])]}")

Final class assigned: versicolor
True class: versicolor

label_binarized

from sklearn.preprocessing import label_binarize
from pprint import pprint

# Original class labels
y_train = np.array([0, 1, 2, 0, 1, 2, 1, 0])

# Binarize the labels
y_train_binarized = label_binarize(y_train, classes=[0, 1, 2])

# Assume y_train_binarized contains the binarized labels
print("Binarized labels:\n", y_train_binarized)

# Convert binarized labels back to the original numerical values
original_labels = [np.argmax(b) for b in y_train_binarized]
print("Original labels:\n", original_labels)

Binarized labels:
 [[1 0 0]
 [0 1 0]
 [0 0 1]
 [1 0 0]
 [0 1 0]
 [0 0 1]
 [0 1 0]
 [1 0 0]]
Original labels:
 [np.int64(0), np.int64(1), np.int64(2), np.int64(0), np.int64(1), np.int64(2), np.int64(1), np.int64(0)]

Marcel Turcotte

Marcel.Turcotte@uOttawa.ca

École de science informatique et de génie électrique (SIGE)

Université d’Ottawa

Attribution: “An image of a sad Chihuahua amigurumi with a birthday hat.” Générée par DALL-E, via ChatGPT (GPT-4), OpenAI, 16 septembre, 2024.