Évaluation des modèles

CSI 4506 - Automne 2025

Marcel Turcotte

Version: oct. 7, 2025 09h52

Préambule

Message du jour

Dans une récente interview avec Bloomberg Technology, Demis Hassabis discute du travail innovant d’Isomorphic Labs dans l’accélération significative des processus de développement de médicaments. Voici un résumé des réalisations notables de Hassabis :

• Prodige des échecs dès son jeune âge, Hassabis a commencé à jouer à quatre ans et a atteint un classement Elo d’environ 2300 à l’âge de 13 ans.
• Il a cofondé DeepMind en 2010 aux côtés de Shane Legg et Mustafa Suleyman, où il est actuellement PDG.
• Sous sa direction, DeepMind a été à l’avant-garde de plusieurs avancées révolutionnaires en intelligence artificielle, y compris le développement de AlphaGo et, notamment, AlphaFold et AlphaFold2, qui sont essentiels dans la prédiction de la structure des protéines.
• En reconnaissance de ses contributions à la prédiction de la structure des protéines, Hassabis a reçu le Prix Nobel de Chimie en 2024.
• En 2021, il a fondé Isomorphic Labs, qui se concentre sur l’application de l’IA à la découverte de médicaments et à la science translationnelle.
• “The Thinking Game” est un documentaire qui explore la vie de Demis Hassabis, l’évolution de DeepMind, et la quête de l’intelligence artificielle générale (IAG).

Dans un domaine connexe, un article intitulé “Quelles maladies aurez-vous dans 20 ans ? Cette IA prédit avec précision vos risques” a été publié dans Nature le 17 septembre 2025. Ce bref article d’actualité discute de Delphi-2M, un grand modèle de langage conçu pour analyser les dossiers médicaux et les facteurs de mode de vie d’un individu afin de fournir des évaluations de risque pour plus de 1 000 maladies. Un podcast est également disponible pour plus de perspectives.

Demis Hassabis : Le PDG qui travaille à résoudre le cancer avec l’IA, Bloomberg Technology, 2025-09-14.

Résumé

Ce cours aborde l’évaluation des modèles de classification, en se concentrant sur les matrices de confusion et les métriques clés : exactitude, précision, rappel et score \(F_1\). Il traite des limites de l’exactitude dans les ensembles de données déséquilibrés, en introduisant les moyennes micro et macro. Le compromis précision-rappel et l’analyse ROC, y compris l’AUC, sont également explorés. Des perspectives pratiques sont fournies à travers des implémentations en Python comme la régression logistique via la descente de gradient.

Résultats d’apprentissage

• Décrire la structure et le rôle de la matrice de confusion dans l’évaluation des modèles.
• Calculer et interpréter l’exactitude, la précision, le rappel et le score \(F_1\).
• Identifier les pièges de l’utilisation de l’exactitude avec des ensembles de données déséquilibrés.
• Différencier entre les moyennes micro et macro pour les métriques de performance.
• Analyser les compromis précision-rappel et construire des courbes ROC, y compris le calcul de l’AUC.
• Implémenter le calcul des courbes ROC et de l’AUC en Python.

Mesures de performance

Matrice de confusion

	Positif (Prédit)	Négatif (Prédit)
Positif (Réel)	Vrai positif (VP)	Faux négatif (FN)
Négatif (Réel)	Faux positif (FP)	Vrai négatif (VN)

• Dans l’analyse statistique, les faux positifs (FP) sont communément appelés erreurs de type I, et les faux négatifs (FN) sont connus sous le nom d’erreurs de type II.
• Les éléments de la diagonale représentent les résultats correctement prédits, à savoir les vrais positifs (VP) et les vrais négatifs (VN).
• À l’inverse, les éléments hors diagonale correspondent aux prédictions incorrectes, spécifiquement les faux positifs (FP) et les faux négatifs (FN).
• La matrice de confusion encapsule toutes les informations essentielles nécessaires pour évaluer la performance d’un modèle de classification.
• Bien que la matrice de confusion fournisse une vue d’ensemble, des mesures plus concises telles que l’exactitude, la précision, le rappel, et le score F\(_1\) sont souvent plus intuitives et pratiques pour résumer la performance du modèle.

Une matrice de confusion est un tableau résumant la performance d’un algorithme de classification (ici pour une tâche de classification binaire).

ConfusionMatrixDisplay

import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression

seed = 42

X, y = make_classification(n_samples = 500, random_state=seed)

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state=0)

clf = LogisticRegression(random_state=seed)

clf.fit(X_train, y_train)

predictions = clf.predict(X_test)

cm = confusion_matrix(y_test, predictions, labels=[1, 0])

disp = ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=["Positive", "Negative"])

disp.plot()
plt.show()

Nous utilisons la fonction make_classification pour générer un jeu de données synthétique, qui est ensuite analysé à l’aide d’un modèle de LogisticRegression. Pour les deux fonctions confusion_matrix et ConfusionMatrixDisplay, nous configurons les étiquettes pour nous assurer que la classe ‘Positive’ précède, en accord avec les données tabulaires présentées à l’écran précédent. La matrice de confusion résultante donne les valeurs suivantes : Vrais Positifs (VP) = 37, Faux Négatifs (FN) = 10, Faux Positifs (FP) = 3, et Vrais Négatifs (VN) = 50.

Matrice de confusion

Étant donné un ensemble de test avec \(N\) exemples et un classificateur \(h(x) :\)

\[ C_{i,j} = \sum_{k = 1}^N [y_k = i \wedge h(x_k) = j] \]

Où \(C\) est une matrice \(l \times l\), pour un ensemble de données avec \(l\) classes.

Examinons maintenant le cas général d’une matrice de confusion avec \(l\) classes, qui peut initialement sembler “confus” à comprendre.

Une matrice de confusion \(C\) est définie de telle sorte que chaque élément \(C_{i,j}\) représente le nombre d’observations appartenant réellement à la classe \(i\) mais prédites comme appartenant à la classe \(j\).

Matrice de confusion

• Le nombre total d’exemples de la classe (réelle) \(i\) est \[ C_{i \cdot} = \sum_{j=1}^l C_{i,j} \]

• Le nombre total d’exemples assignés à la classe (prédite) \(j\) par le classificateur \(h\) est \[ C_{\cdot j} = \sum_{i=1}^l C_{i,j} \]

Matrice de confusion

• Les termes sur la diagonale indiquent le nombre total d’exemples classés correctement par le classificateur \(h\). Ainsi, le nombre d’exemples correctement classés est \[ \sum_{i=1}^l C_{i,i} \]

• Les termes non-diagonaux représentent les erreurs de classification.

Matrice de confusion - multi-classes

Pour évaluer la performance dans un contexte multi-classes, on dérive généralement des métriques “un-contre-tous” pour chaque classe à partir de la matrice de confusion. Ces métriques sont ensuite moyennées en utilisant des schémas de pondération spécifiques.

Matrice de confusion - multi-classes

Utilisation des données du jeu de données textuel 20 newsgroups de scikit-learn.org.

Matrice de confusion - vrai positif

comp.graphics est la classe vraie (\(i\)).

Matrice de confusion - faux positif

comp.graphics est la classe vraie (\(i\)).

Matrice de confusion - faux négatif

comp.graphics est la classe vraie (\(i\)).

Matrice de confusion - vrai négatif

comp.graphics est la classe vraie (\(i\)).

Matrice de confusion - multi-classes

comp.graphics est la classe vraie (\(i\)).

Multi-classes

Pour évaluer la performance dans un contexte multi-classes, on dérive généralement des métriques “un-contre-tous” pour chaque classe à partir de la matrice de confusion. Ces métriques sont ensuite moyennées en utilisant des schémas de pondération spécifiques.

• Vrais Positifs (\(\mathrm{TP}_i\)) : Entrée diagonale \(C_{i,i}\)
• Faux Positifs (\(\mathrm{FP}_i\)) : Somme de la colonne \(i\) excluant \(C_{i,i}\)
• Faux Négatifs (\(\mathrm{FN}_i\)) : Somme de la ligne \(i\) excluant \(C_{i,i}\)
• Vrais Négatifs (\(\mathrm{TN}_i\)) : \(N - (\mathrm{TP}_i + \mathrm{FP}_i + \mathrm{FN}_i)\)

Multi-classes

Pour évaluer la performance dans un contexte multi-classes, on dérive généralement des métriques “un-contre-tous” pour chaque classe à partir de la matrice de confusion. Ces métriques sont ensuite moyennées en utilisant des schémas de pondération spécifiques.

• \(\mathrm{TP}_i = C_{i,i}\)
• \(\mathrm{FP}_i = \sum_{k \ne i} C_{k,i}\)
• \(\mathrm{FN}_i = \sum_{k \ne i} C_{i,k}\)
• \(\mathrm{TN}_i = \sum_{j \ne i} \sum_{k \ne i} C_{j,k}\)

sklearn.metrics.confusion_matrix

from sklearn.metrics import confusion_matrix

y_actual = [0, 0, 0, 1, 1, 1, 1, 1, 1, 1]
y_pred   = [0, 1, 1, 0, 0, 0, 1, 1, 1, 1]

confusion_matrix(y_actual,y_pred)

array([[1, 2],
       [3, 4]])

tn, fp, fn, tp = confusion_matrix(y_actual, y_pred).ravel().tolist()
(tn, fp, fn, tp)

(1, 2, 3, 4)

Par défaut, sklearn.metrics.confusion_matrix détermine l’ensemble des étiquettes à partir des données (\(\textrm{y_true} \cup \textrm{y_pred}\)), et ensuite :

• Il les trie par ordre croissant (ce qui, pour les chaînes ou les types mixtes, correspond à l’ordre lexicographique de Python).
• Il construit ensuite la matrice de sorte que la ligne i corresponde à la classe réelle avec l’étiquette labels[i], et la colonne j corresponde à la classe prédite avec l’étiquette labels[j].

Donc, si vous ne passez pas labels=..., vous pouvez obtenir une matrice de confusion avec un ordre de classes qui n’est pas celui que vous attendez — surtout si vos classes sont des chaînes, ou si vous supposez que l’ordre suit l’ordre d’apparition dans le jeu de données.

Exemple

from sklearn.metrics import confusion_matrix

y_true = ["dog", "cat", "cat", "dog"]
y_pred = ["dog", "dog", "cat", "cat"]

print(confusion_matrix(y_true, y_pred))

Résultat :

[[1 1]
 [1 1]]

Ici, les lignes/colonnes sont dans l’ordre lexicographique : ["cat", "dog"]. Donc la matrice est :

• Ligne 0 : vrai = “chat”
• Ligne 1 : vrai = “chien”

Contrôler l’ordre

Pour imposer un ordre spécifique, vous devez passer l’argument labels :

confusion_matrix(y_true, y_pred, labels=["dog", "cat"])

Cela permutera l’ordre des lignes/colonnes en conséquence.

Prédiction parfaite

y_actual = [0, 1, 0, 0, 1, 1, 1, 0, 1, 1]
y_pred   = [0, 1, 0, 0, 1, 1, 1, 0, 1, 1]

confusion_matrix(y_actual,y_pred)

array([[4, 0],
       [0, 6]])

tn, fp, fn, tp = confusion_matrix(y_actual, y_pred).ravel().tolist()  
(tn, fp, fn, tp)

(4, 0, 0, 6)

Lorsqu’un algorithme fait une classification parfaite, toutes les valeurs non nulles (0) de la matrice de confusion apparaissent exclusivement le long de sa diagonale.

Toutes les entrées hors diagonale, qui représentent des erreurs de classification, seront nulles (0).

Matrice de confusion

from sklearn.datasets import load_digits

import numpy as np
np.random.seed(42)

digits = load_digits()

X = digits.data
y = digits.target

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.1)

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)

from sklearn.linear_model import LogisticRegression
from sklearn.multiclass import OneVsRestClassifier

clf = OneVsRestClassifier(LogisticRegression())

clf = clf.fit(X_train, y_train)

import matplotlib.pyplot as plt
from sklearn.metrics import ConfusionMatrixDisplay

X_test = scaler.transform(X_test)
y_pred = clf.predict(X_test)

ConfusionMatrixDisplay.from_predictions(y_test, y_pred)
plt.show()

L’image affiche une carte thermique de la matrice de confusion pour la tâche de classification des chiffres. Cette tâche, un problème de classification multiclasses, a été traitée en utilisant OneVsRestClassifier et LogisticRegression.

La matrice de confusion résume les prédictions faites sur l’ensemble de test, qui est un sous-ensemble des données qui n’a pas été utilisé pour l’entraînement ni pour le prétraitement avec StandardScaler.

La matrice de confusion encapsule tous les résultats de l’application du classificateur sur l’ensemble de test. Cependant, pour résumer ces informations plus succinctement, nous nous référons souvent à des métriques de performance.

Matrice de confusion pour l’exemple de chiffres manuscrits présenté lors du cours précédent.

Visualisation des erreurs

mask = (y_test == 9) & (y_pred == 8)

X_9_as_8 = X_test[mask]

y_9_as_8 = y_test[mask]

import numpy as np
np.random.seed(42)

from sklearn.datasets import load_digits
digits = load_digits()

X = digits.data
y = digits.target

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.1)

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)

from sklearn.linear_model import LogisticRegression
from sklearn.multiclass import OneVsRestClassifier

clf = OneVsRestClassifier(LogisticRegression())

clf = clf.fit(X_train, y_train)

X_test = scaler.transform(X_test)
y_pred = clf.predict(X_test)

mask = (y_test == 9) & (y_pred == 8)

X_9_as_8 = X_test[mask]

y_9_as_8 = y_test[mask]

import matplotlib.pyplot as plt

plt.figure(figsize=(4,2))

for index, (image, label) in enumerate(zip(X_9_as_8, y_9_as_8)):
    plt.subplot(1, len(X_9_as_8), index + 1)
    plt.imshow(np.reshape(image, (8,8)), cmap=plt.cm.gray)
    plt.title(f'y = {label}')

Dans la matrice de confusion à l’écran précédent, nous avions vu qu’il y avait des exemples pour lesquels l’étiquette réelle était 9, mais la prédiction était 8. Nous pouvons visualiser les exemples pour voir si nous comprenons la nature de ces erreurs.

Matrice de confusion

Il est souvent préférable de résumer la performance du classificateur par une seule métrique.

Exactitude

Quelle est l’exactitude de ce résultat ?

\[ \mathrm{exactitude} = \frac{\mathrm{VP}+\mathrm{VN}}{\mathrm{VP}+\mathrm{VN}+\mathrm{FP}+\mathrm{FN}} = \frac{\mathrm{VP}+\mathrm{VN}}{\mathrm{N}} \]

from sklearn.metrics import accuracy_score

y_actual = [0, 0, 0, 1, 1, 1, 1, 1, 1, 1]
y_pred   = [0, 1, 1, 0, 0, 0, 1, 1, 1, 1]

accuracy_score(y_actual,y_pred)

0.5

Dans le contexte francophone, le terme « accuracy » se traduit généralement par « exactitude ». Il est important de noter que certaines applications utilisent à tort le terme « précision » pour désigner « accuracy ». Or, « précision » correspond en réalité au terme anglais « precision », qui possède une signification distincte.

L’exactitude est le rapport entre les instances correctement prédites et le nombre total de prédictions.

Exactitude

y_actual = [0, 1, 0, 0, 1, 1, 1, 0, 1, 1]
y_pred   = [1, 0, 1, 1, 0, 0, 0, 1, 0, 0]

accuracy_score(y_actual,y_pred)

0.0

y_actual = [0, 1, 0, 0, 1, 1, 1, 0, 1, 1]
y_pred   = [0, 1, 0, 0, 1, 1, 1, 0, 1, 1]

accuracy_score(y_actual,y_pred)

1.0

L’exactitude est un nombre entre 0 (tout faux) et 1 (parfait).

L’exactitude peut être trompeuse

y_actual = [0, 0, 0, 0, 1, 1, 0, 0, 0, 0]
y_pred   = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

accuracy_score(y_actual,y_pred)

0.8

L’exactitude peut être trompeuse dans le contexte du déséquilibre de classe, car elle reflète de manière disproportionnée la performance sur la classe majoritaire, masquant ainsi une mauvaise performance sur la classe minoritaire.

À mesure que le déséquilibre de classe augmente, la mesure d’exactitude devient de plus en plus trompeuse.

Pourquoi est-ce problématique ?

Précision

Aussi connu sous le nom de valeur prédictive positive (PPV).

\[ \mathrm{précision} = \frac{\mathrm{VP}}{\mathrm{VP}+\mathrm{FP}} \]

from sklearn.metrics import precision_score

y_actual = [0, 0, 0, 1, 1, 1, 1, 1, 1, 1]
y_pred   = [0, 1, 1, 0, 0, 0, 1, 1, 1, 1]

precision_score(y_actual, y_pred)

0.6666666666666666

Pouvez-vous penser à un problème ou une situation où la précision est primordiale ?

Un exemple classique : le dépistage médical pour une maladie rare mais grave.

• Supposons que vous avez un test pour une maladie avec une prévalence très faible (disons 1 sur 10 000).
• Si votre modèle prédit “positif” trop vaguement, vous générerez de nombreux faux positifs.
• Ici, la précision (la proportion des positifs prédits qui sont réellement des vrais positifs) est cruciale :

\[ \text{Précision} = \frac{\text{VP}}{\text{VP} + \text{FP}} \]

• Une haute précision signifie que lorsque le test dit “positif”, il est très probablement correct.
• Cela réduit l’anxiété inutile, les coûts et les procédures de suivi pour les patients incorrectement signalés.

Autres contextes réels où la précision est essentielle :

• Détection de spam : Une haute précision garantit que les e-mails classés comme spam le sont vraiment (minimisant les faux positifs qui cacheraient de vrais e-mails).
• Recherche de documents juridiques / e-discovery : Une haute précision garantit que les documents renvoyés sont pertinents, réduisant le temps perdu sur des résultats non pertinents.
• Systèmes de recommandation : Une haute précision signifie que les articles recommandés sont très susceptibles d’être intéressants, améliorant la confiance des utilisateurs.

La précision est la proportion de prédictions positives vraies parmi toutes les prédictions positives.

La précision seule ne suffit pas

y_actual = [0, 0, 0, 1, 1, 1, 1, 1, 1, 1]
y_pred   = [0, 0, 0, 0, 0, 0, 1, 0, 0, 0]

precision_score(y_actual,y_pred)

1.0

Un algorithme qui fait un petit nombre de prédictions à haute confiance pourrait atteindre un score de précision élevé, mais cela ne sera pas nécessairement utile.

Rappel

Aussi connu sous le nom de sensibilité ou taux de vrais positifs (TPR)

\[ \mathrm{rappel} = \frac{\mathrm{VP}}{\mathrm{VP}+\mathrm{FN}} \]

from sklearn.metrics import recall_score

y_actual = [0, 0, 0, 1, 1, 1, 1, 1, 1, 1]
y_pred   = [0, 1, 1, 0, 0, 0, 1, 1, 1, 1]

recall_score(y_actual,y_pred)

0.5714285714285714

Pouvez-vous penser à un problème ou une situation où le rappel est primordial ?

Un exemple où le rappel est la mesure critique : diagnostic du cancer (dépistage des tumeurs malignes).

• Ici, les faux négatifs (manquer un cas réel de cancer) sont beaucoup plus dangereux que les faux positifs.
• Le rappel mesure la proportion de vrais positifs correctement identifiés :

\[ \text{Rappel} = \frac{\text{VP}}{\text{VP} + \text{FN}} \]

• Un rappel élevé signifie que le test détecte presque tous les patients atteints de cancer, même s’il génère également quelques fausses alertes.
• Manquer un cas réel (rappel faible) pourrait signifier qu’un patient ne reçoit pas de traitement à temps — une erreur beaucoup plus grave que d’investiguer quelques faux positifs supplémentaires.

Autres contextes réels où le rappel est le plus important :

• Sécurité / Détection d’intrusions : Mieux vaut signaler toute activité suspecte (même avec des faux positifs) que de manquer une véritable attaque.
• Moteurs de recherche : Pour certaines requêtes (par exemple, recherche de précédents juridiques, recherche de littérature médicale), le rappel garantit que vous récupérez tous les documents pertinents.
• Systèmes de réponse d’urgence : Pour les alertes de catastrophes naturelles, un rappel élevé garantit qu’aucune menace réelle ne passe inaperçue.

Rappel est la proportion d’instances positives correctes identifiées parmi toutes les instances réellement positives.

Score F\(_1\)

\[ \begin{align*} F_1~\mathrm{score} &= \frac{2}{\frac{1}{\mathrm{précision}}+\frac{1}{\mathrm{rappel}}} = 2 \times \frac{\mathrm{précision}\times\mathrm{rappel}}{\mathrm{précision}+\mathrm{rappel}} \\ &= \frac{\mathrm{VP}}{\mathrm{VP}+\frac{\mathrm{FN}+\mathrm{FP}}{2}} \end{align*} \]

from sklearn.metrics import f1_score

y_actual = [0, 0, 0, 1, 1, 1, 1, 1, 1, 1]
y_pred   = [0, 1, 1, 0, 0, 0, 1, 1, 1, 1]

f1_score(y_actual,y_pred)

0.6153846153846154

• La moyenne harmonique met davantage l’accent sur les valeurs plus faibles, tandis que la moyenne arithmétique traite toutes les valeurs de manière égale.
• Utiliser la moyenne harmonique garantit qu’un score élevé n’est obtenu que lorsque la précision et le rappel sont tous deux élevés, offrant ainsi une mesure plus holistique des performances d’un classificateur dans des scénarios avec des ensembles de données déséquilibrés.
• Le score F\(_1\) favorise les classificateurs qui réalisent un équilibre entre la précision et le rappel.
• Augmenter le rappel entraîne souvent une diminution de la précision, et vice versa. Ce phénomène est connu sous le nom de compromis précision/rappel.

F\(_1\) est la moyenne harmonique de la précision et du rappel.

Moyennes micro et macro

Définition

Le problème de déséquilibre de classes est un scénario où le nombre d’instances dans une classe dépasse significativement le nombre d’instances dans d’autres classes.

Les modèles ont tendance à être biaisés en faveur de la classe majoritaire, ce qui conduit à une mauvaise performance sur la classe minoritaire.

Les mesures d’évaluation standard comme la précision peuvent être trompeuses en présence d’un déséquilibre de classes.

Mesures de performance micro

• Les mesures de performance micro agrègent les contributions de toutes les instances pour calculer des mesures de performance moyennes comme la précision, le rappel, ou le score F1.
• Cette approche traite chaque prédiction individuelle de manière égale, indépendamment de sa classe, car elle prend en compte le nombre total de vrais positifs, de faux positifs et de faux négatifs à travers toutes les classes.
• Par conséquent, les mesures micro sont particulièrement sensibles à la performance sur les classes fréquentes car elles sont plus nombreuses et ont donc une plus grande influence sur la mesure globale.

Mesures de performance macro

• Les mesures de performance macro calculent la mesure de performance indépendamment pour chaque classe, puis font la moyenne de ces mesures.
• Cette approche traite chaque classe de manière égale, indépendamment de sa fréquence, fournissant une évaluation qui considère également la performance à travers les classes fréquentes et peu fréquentes.
• Par conséquent, les mesures macro sont moins sensibles à la performance sur les classes fréquentes.

Multi-classe

Lors du calcul de la précision, du rappel et de \(F_1\), on calcule généralement les métriques “un-contre-tous” pour chaque classe. Ensuite, on les moyenne en utilisant des schémas de pondération (macro, micro).

• Vrais Positifs (\(\mathrm{TP}_i\)) : Entrée diagonale \(C_{i,i}\)
• Faux Positifs (\(\mathrm{FP}_i\)) : Somme de la colonne \(i\) à l’exception de \(C_{i,i}\)
• Faux Négatifs (\(\mathrm{FN}_i\)) : Somme de la ligne \(i\) à l’exception de \(C_{i,i}\)
• Vrais Négatifs (\(\mathrm{TN}_i\)) : \(N - (\mathrm{TP}_i + \mathrm{FP}_i + \mathrm{FN}_i)\)

Multi-classe

Lors du calcul de la précision, du rappel et de \(F_1\), on calcule généralement les métriques “un-contre-tous” pour chaque classe. Ensuite, on les moyenne en utilisant des schémas de pondération (macro, micro).

• \(\mathrm{TP}_i = C_{i,i}\)
• \(\mathrm{FP}_i = \sum_{k \ne i} C_{k,i}\)
• \(\mathrm{FN}_i = \sum_{k \ne i} C_{i,k}\)
• \(\mathrm{TN}_i = \sum_{j \ne i} \sum_{k \ne i} C_{j,k}\)

Micro/Macro

from sklearn.metrics import ConfusionMatrixDisplay

# Données d'exemple
y_true = ['Chat'] * 42 + ['Chien'] *  7 + ['Renard'] * 11
y_pred = ['Chat'] * 39 + ['Chien'] *  1 + ['Renard'] *  2 + \
         ['Chat'] *  4 + ['Chien'] *  3 + ['Renard'] *  0 + \
         ['Chat'] *  5 + ['Chien'] *  1 + ['Renard'] *  5

ConfusionMatrixDisplay.from_predictions(y_true, y_pred)

Le jeu de données peut être conceptualisé comme résultant d’une tâche de classification d’images, impliquant des images de chats, chiens et renards. Reflétant les tendances courantes observées sur internet, les images de chats sont disproportionnellement représentées, entraînant un problème de déséquilibre des classes.

Précision micro/macro

from sklearn.metrics import classification_report, precision_score

print(classification_report(y_true, y_pred), "\n")

print("Précision micro : {:.2f}".format(precision_score(y_true, y_pred, average='micro')))
print("Précision macro : {:.2f}".format(precision_score(y_true, y_pred, average='macro')))

              precision    recall  f1-score   support

        Chat       0.81      0.93      0.87        42
       Chien       0.60      0.43      0.50         7
      Renard       0.71      0.45      0.56        11

    accuracy                           0.78        60
   macro avg       0.71      0.60      0.64        60
weighted avg       0.77      0.78      0.77        60
 

Précision micro : 0.78
Précision macro : 0.71

Précision micro/macro

• La précision moyenne macro est calculée comme la moyenne des scores de précision¹ pour chaque classe : \(\frac{0.81 + 0.60 + 0.71}{3} = 0.71\).

• Tandis que, la précision moyenne micro est calculée en utilisant la formule, \(\frac{TP}{TP+FP}\) et les données de toute la matrice de confusion \(\frac{39+3+5}{39+3+5+9+2+2} = \frac{47}{60} = 0.78\)

La haute précision moyenne micro observée ici est principalement due à la haute précision et au grand nombre d’exemples dans la classe majoritaire, Chat. Cela masque la performance relativement médiocre du classificateur sur les classes minoritaires, Chien et Renard.

Dans un jeu de données équilibré, les métriques micro-moyenne et macro-moyenne donnent des scores similaires.

Cependant, dans un jeu de données déséquilibré, des différences significatives dans les performances du classificateur entre les classes majoritaires et minoritaires entraîneront des scores micro-moyenne et macro-moyenne divergents. En particulier, le classificateur a tendance à sous-performer sur les classes minoritaires, conduisant à ces écarts.

Dans les métriques macro-moyennes, chaque classe contribue également au calcul final de la métrique, indépendamment du nombre d’exemples qu’elle contient. Cela signifie que les métriques de performance pour chaque classe sont calculées indépendamment puis moyennées, sans tenir compte de la proportion d’instances que chaque classe représente dans le jeu de données. Par conséquent, la macro-moyenne garantit que chaque classe a un impact égal sur la métrique globale, ce qui peut être particulièrement utile dans les cas où la distribution des classes est déséquilibrée.

1. Par conséquent, la précision moyenne macro reste inchangée par le nombre variable d’exemples dans les différentes classes.

Rappel micro/macro

              precision    recall  f1-score   support

        Chat       0.81      0.93      0.87        42
       Chien       0.60      0.43      0.50         7
      Renard       0.71      0.45      0.56        11

    accuracy                           0.78        60
   macro avg       0.71      0.60      0.64        60
weighted avg       0.77      0.78      0.77        60
 

Rappel micro : 0.78
Rappel macro : 0.60

Rappel micro/macro

• Le rappel moyen macro est calculé comme la moyenne des scores de rappel pour chaque classe : \(\frac{0.93 + 0.43 + 0.45}{3} = 0.60\).

• Tandis que, le rappel moyen micro est calculé en utilisant la formule, \(\frac{TP}{TP+FN}\) et les données de toute la matrice de confusion \(\frac{39+3+5}{39+3+5+3+4+6} = \frac{39}{60} = 0.78\)

Exemple

Utilisation du jeu de données textuelles 20 newsgroups de scikit-learn.org.

Comprend environ 18 000 articles de newsgroups sur 20 sujets.

## https://scikit-learn.org/stable/auto_examples/text/plot_document_classification_20newsgroups.html

from time import time

## Charger le jeu de données

from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import TfidfVectorizer

categories = [
    "alt.atheism",
    "talk.religion.misc",
    "comp.graphics",
    "sci.space",
]

def size_mb(docs):
    return sum(len(s.encode("utf-8")) for s in docs) / 1e6

def load_dataset(verbose=False, remove=()):
    """Charger et vectoriser le jeu de données des 20 newsgroups."""

    data_train = fetch_20newsgroups(
        subset="train",
        categories=categories,
        shuffle=True,
        random_state=42,
        remove=remove,
    )

    data_test = fetch_20newsgroups(
        subset="test",
        categories=categories,
        shuffle=True,
        random_state=42,
        remove=remove,
    )

    # l'ordre des étiquettes dans `target_names` peut être différent de `categories`
    target_names = data_train.target_names

    # diviser la cible en un ensemble d'entraînement et un ensemble de test
    y_train, y_test = data_train.target, data_test.target

    # Extraction des attributs des données d'entraînement à l'aide d'un vectoriseur creux
    t0 = time()
    vectorizer = TfidfVectorizer(
        sublinear_tf=True, max_df=0.5, min_df=5, stop_words="english"
    )
    X_train = vectorizer.fit_transform(data_train.data)
    duration_train = time() - t0

    # Extraction des attributs des données de test en utilisant le même vectoriseur
    t0 = time()
    X_test = vectorizer.transform(data_test.data)
    duration_test = time() - t0

    feature_names = vectorizer.get_feature_names_out()

    if verbose:
        # calculer la taille des données chargées
        data_train_size_mb = size_mb(data_train.data)
        data_test_size_mb = size_mb(data_test.data)

        # print(
        #     f"{len(data_train.data)} documents - "
        #     f"{data_train_size_mb:.2f}MB (ensemble d'entraînement)"
        # )
        # print(f"{len(data_test.data)} documents - {data_test_size_mb:.2f}MB (ensemble de test)")
        # print(f"{len(target_names)} catégories")
        # print(
        #     f"vectorisation de l'entraînement terminée en {duration_train:.3f}s "
        #     f"à {data_train_size_mb / duration_train:.3f}MB/s"
        # )
        # print(f"n_samples: {X_train.shape[0]}, n_features: {X_train.shape[1]}")
        # print(
        #     f"vectorisation du test terminée en {duration_test:.3f}s "
        #     f"à {data_test_size_mb / duration_test:.3f}MB/s"
        # )
        # print(f"n_samples: {X_test.shape[0]}, n_features: {X_test.shape[1]}")

    return X_train, X_test, y_train, y_test, feature_names, target_names

X_train, X_test, y_train, y_test, feature_names, target_names = load_dataset(
    verbose=True
)

## Entraînement et prédiction

from sklearn.linear_model import RidgeClassifier

clf = RidgeClassifier(tol=1e-2, solver="sparse_cg")
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)

## Afficher la matrice de confusion

from sklearn.metrics import ConfusionMatrixDisplay

fig, ax = plt.subplots(figsize=(10, 5))
ConfusionMatrixDisplay.from_predictions(y_test, y_pred, ax=ax)
ax.xaxis.set_ticklabels(target_names)
ax.yaxis.set_ticklabels(target_names)
_ = ax.set_title(
    f"Matrice de confusion pour {clf.__class__.__name__}"
)

Exemple

Exemple

cm = confusion_matrix(y_test, y_pred)

VP, FP, FN, VN

def true_positive(cm, i):
    return cm[i,i] # entrée diagonale i,i

def false_positive(cm, i):
    return np.sum(cm[:, i]) - cm[i,i] # colonne - VP_i

def false_negative(cm, i):
    return np.sum(cm[i, :]) - cm[i,i] # ligne - VP_i

def true_negative(cm, i):
    N = cm.sum()
    TP = true_positive(cm, i)
    FP = false_positive(cm, i)
    FN = false_negative(cm, i)
    return N - (TP + FP + FN)

Précision

def precision_micro(cm):
    _, l = cm.shape
    tp = fp = 0
    for i in range(l):
        tp += true_positive(cm, i)
        fp += false_positive(cm, i)
    return tp / (tp+fp)

def precision_macro(cm):
    _, l = cm.shape
    precision = 0
    for i in range(l):
        tp = true_positive(cm, i)
        fp = false_positive(cm, i)
        precision += tp/(tp+fp)
    return precision/l

Précision moyenne micro

\[ \frac{(258+380+371+199)}{(258+380+371+199)+(40+38+22+45)} \] où

• 40 = 2 + 1 + 37
• 38 = 7 + 22 + 9
• 22 = 12 + 4 + 6
• 45 = 42 + 3 + 0

89.28307465 %

Précision moyenne macro

• \(\mathrm{Precision}_0 = \frac{258}{258+(2+1+37)} = 0.8657718121\)
• \(\mathrm{Precision}_1 = \frac{380}{380+(7+22+9)} = 0.9090909091\)
• \(\mathrm{Precision}_2 = \frac{371}{371+(12+4+6)} = 0.9440203562\)
• \(\mathrm{Precision}_3 = \frac{199}{199+(42+3+0)} = 0.8155737705\)

\(\mathrm{Precision}_3 = \frac{0.8657718121 + 0.9090909091 + 0.9440203562 + 0.8155737705}{4}\)

88.3614212 %

Rappel

def rappel_micro(cm):
    _, l = cm.shape
    tp = fn = 0
    for i in range(l):
        tp += true_positive(cm, i)
        fn += false_negative(cm, i)
    return tp / (tp+fn)

def rappel_macro(cm):
    _, l = cm.shape
    rappel = 0
    for i in range(l):
        tp = true_positive(cm, i)
        fn = false_negative(cm, i)
        rappel += tp / (tp+fn)
    return rappel/l

Données médicales

Considérons un ensemble de données médicales, telles que celles impliquant des tests de diagnostic ou de l’imagerie, comprenant 990 échantillons normaux et 10 échantillons anormaux (tumeur). Cela représente la vérité terrain.

Données médicales

              precision    recall  f1-score   support

      Normal       1.00      0.99      1.00       990
      Tumour       0.55      0.60      0.57        10

    accuracy                           0.99      1000
   macro avg       0.77      0.80      0.78      1000
weighted avg       0.99      0.99      0.99      1000
 

Précision micro : 0.99
Précision macro : 0.77


Rappel micro : 0.99
Rappel macro : 0.80

La précision pour la classe Tumour est faible. Cependant, en raison de la petite taille de l’échantillon, cela n’impacte pas significativement la précision moyennée par micro.

Compromis précision-rappel

Chiffres manuscrits (revisités)

Chargement du jeu de données

import numpy as np
np.random.seed(42)

from sklearn.datasets import fetch_openml

digits = fetch_openml('mnist_784', as_frame=False)
X, y = digits.data, digits.target

Tracé des cinq premiers exemples

Ces images ont des dimensions de \(28 \times 28\) pixels.

Tâche de classification binaire

# Création d'une tâche de classification binaire (un contre tous)

some_digit = X[0]
some_digit_y = y[0]

y = (y == some_digit_y)
y

array([ True, False, False, ..., False,  True, False], shape=(70000,))

# Création des ensembles d'entraînement et de test
from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.1, random_state=42)

SGDClassifier

from sklearn.linear_model import SGDClassifier

clf = SGDClassifier()
clf.fit(X_train, y_train)

clf.predict(X[0:5]) # petite vérification de bon sens

array([ True, False, False, False, False])

Le SGDClassifier est un classificateur linéaire qui utilise la descente de gradient stochastique (SGD) pour l’entraînement. Comparé à LogisticRegression, il peut offrir des temps d’entraînement plus rapides, particulièrement pour les grands ensembles de données. De plus, SGDClassifier permet l’ajustement du seuil de décision dans les exemples suivants.

Performance

from sklearn.metrics import accuracy_score

y_pred = clf.predict(X_test)

accuracy_score(y_test, y_pred)

0.9684285714285714

Wow!

Pas si vite

from sklearn.dummy import DummyClassifier

dummy_clf = DummyClassifier()

dummy_clf.fit(X_train, y_train)

y_pred = dummy_clf.predict(X_test)

accuracy_score(y_test, y_pred)

0.906

Pourquoi la précision est-elle si élevée alors que ce classificateur ignore les données d’entrée ?

La précision élevée est attribuée à la distribution des classes dans le jeu de données. Environ 10 % des échantillons correspondent au chiffre ‘5’, qui est la classe positive dans notre tâche de classification binaire. Par conséquent, environ 90 % des échantillons ne sont pas ‘5’ et appartiennent à la classe négative. Comme le DummyClassifier prédit toujours la classe majoritaire, sa précision est attendue d’être autour de 90 %.

Cela souligne que la précision n’est souvent pas le meilleur indicateur, en particulier lorsqu’on traite des jeux de données déséquilibrés.

Le DummyClassifier dans scikit-learn génère des prédictions sans tenir compte des attributs d’entrée. Par défaut, il prédit systématiquement la classe la plus fréquente dans les données d’entraînement. C’est un classificateur de base simple.

Compromis précision-rappel

Attribution : Géron (2022) Figure 3.4

Compromis précision-rappel

from sklearn.model_selection import cross_val_predict
y_scores = cross_val_predict(clf, X_train, y_train, cv=3, method="decision_function")

from sklearn.metrics import precision_recall_curve

precisions, recalls, thresholds = precision_recall_curve(y_train, y_scores)

threshold = 3000

plt.figure(figsize=(8, 4))  # extra code – it's not needed, just formatting
plt.plot(thresholds, precisions[:-1], "b--", label="Précision", linewidth=2)
plt.plot(thresholds, recalls[:-1], "g-", label="Rappel", linewidth=2)
plt.vlines(threshold, 0, 1.0, "k", "dotted", label="seuil")

# extra code – this section just beautifies and saves Figure 3–5
idx = (thresholds >= threshold).argmax()  # first index ≥ threshold
plt.plot(thresholds[idx], precisions[idx], "bo")
plt.plot(thresholds[idx], recalls[idx], "go")
plt.axis([-50000, 50000, 0, 1])
plt.grid()
plt.xlabel("Seuil")
plt.legend(loc="center right")

plt.show()

À mesure que le seuil de décision diminue, un plus grand nombre d’exemples sont prédits comme positifs, ce qui peut amener le classificateur à finalement étiqueter tous les exemples comme positifs.

Inversement, à mesure que le seuil de décision augmente, moins d’exemples sont classifiés comme positifs, ce qui peut entraîner le classificateur à ne prédire aucun exemple positif.

Pour certaines applications, un classificateur avec une haute précision est essentiel. Par exemple, envisagez un scénario où chaque prédiction nécessite une expérience en laboratoire coûteuse pour vérifier son exactitude, comme dans une entreprise pharmaceutique cherchant à découvrir de nouveaux médicaments. Ici, le classificateur prédit si un composé est actif. Étant donné le coût élevé des expériences pour valider les candidats, l’entreprise donnerait la priorité aux composés les plus prometteurs en premier.

En revanche, considérez un scénario de dépistage du cancer, tel que l’utilisation de mammographies pour détecter le cancer du sein. Dans ce cas, il peut être préférable d’abaisser le seuil de décision, augmentant ainsi le nombre de prédictions faussement positives. Bien que cette approche entraîne plus de patients à subir des tests supplémentaires, comme des biopsies, elle peut potentiellement sauver plus de vies en s’assurant que moins de cas de cancer passent inaperçus.

SGDClassifier est utilisé car il permet de faire varier le seuil de décision (frontière) pour produire un graphique illustrant le compromis précision-rappel. (Géron 2022) 03_classification.ipynb.

Courbe précision/rappel

import matplotlib.patches as patches  # extra code – for the curved arrow

plt.figure(figsize=(5, 5))  # extra code – not needed, just formatting

plt.plot(recalls, precisions, linewidth=2, label="Courbe Précision/Rappel")

# extra code – just beautifies and saves Figure 3–6
plt.plot([recalls[idx], recalls[idx]], [0., precisions[idx]], "k:")
plt.plot([0.0, recalls[idx]], [precisions[idx], precisions[idx]], "k:")
plt.plot([recalls[idx]], [precisions[idx]], "ko",
         label="Point at threshold 3,000")
plt.gca().add_patch(patches.FancyArrowPatch(
    (0.79, 0.60), (0.61, 0.78),
    connectionstyle="arc3,rad=.2",
    arrowstyle="Simple, tail_width=1.5, head_width=8, head_length=10",
    color="#444444"))
plt.text(0.56, 0.62, "Seuil\nsupérieur", color="#333333")
plt.xlabel("Rappel")
plt.ylabel("Précision")
plt.axis([0, 1, 0, 1])
plt.grid()
plt.legend(loc="lower left")

plt.show()

(Géron 2022) 03_classification.ipynb.

Courbe ROC

Courbe ROC

Courbe des caractéristiques de fonctionnement du récepteur (ROC)

• Taux de vrais positifs (TVP) contre taux de faux positifs (TFP)
• Un classificateur idéal a un TVP proche de 1.0 et un TFP proche de 0.0
• \(\mathrm{TVP} = \frac{\mathrm{VP}}{\mathrm{VP}+\mathrm{FN}}\) (rappel, sensibilité)
• Le TVP s’approche de un lorsque le nombre de prédictions faux négatif est faible
• \(\mathrm{TFP} = \frac{\mathrm{FP}}{\mathrm{FP}+\mathrm{VN}}\) (également appelé~[1-spécificité])
• Le TFP s’approche de zéro lorsque le nombre de faux positifs est faible

Les courbes ROC (Receiver Operating Characteristic) sont populaires en apprentissage automatique et en statistiques pour plusieurs raisons :

1. Évaluation de la performance complète : Les courbes ROC offrent une représentation visuelle de la performance d’un classificateur à travers tous les seuils possibles. En traçant le Taux de Vrais Positifs (TVP) contre le Taux de Faux Positifs (TFP), elles permettent aux praticiens d’évaluer le compromis entre sensibilité (rappel) et spécificité.
2. Indépendance au seuil : Contrairement à des métriques comme la précision, les courbes ROC évaluent la performance d’un classificateur sans se baser sur un seuil de décision spécifique. Cela les rend particulièrement utiles pour comparer des modèles à travers différents seuils.
3. Surface sous la courbe (AUC) : La Surface Sous la Courbe ROC (AUC) fournit un résumé en valeur unique de la performance du modèle. L’AUC-ROC est souvent utilisée comme une métrique de référence pour comparer différents modèles, avec des valeurs allant de 0.5 (devinette aléatoire) à 1.0 (classification parfaite).
4. Applicabilité large : Les courbes ROC peuvent être utilisées pour toute tâche de classification binaire et sont facilement étendues aux problèmes multiclasses en utilisant des techniques comme la classification un-contre-tous, ce qui les rend polyvalentes dans l’évaluation des classificateurs.

Courbe ROC

Courbe ROC

idx_for_90_precision = (precisions >= 0.90).argmax()
threshold_for_90_precision = thresholds[idx_for_90_precision]
y_train_pred_90 = (y_scores >= threshold_for_90_precision)

from sklearn.metrics import roc_curve

fpr, tpr, thresholds = roc_curve(y_train, y_scores)

idx_for_threshold_at_90 = (thresholds <= threshold_for_90_precision).argmax()
tpr_90, fpr_90 = tpr[idx_for_threshold_at_90], fpr[idx_for_threshold_at_90]

plt.figure(figsize=(5, 5))  # code supplémentaire – pas nécessaire, juste pour le formatage
plt.plot(fpr, tpr, linewidth=2, label="Courbe ROC")
plt.plot([0, 1], [0, 1], 'k:', label="Courbe ROC du classificateur aléatoire")
plt.plot([fpr_90], [tpr_90], "ko", label="Seuil pour 90% de précision")

# code supplémentaire – juste pour embellir et enregistrer la Figure 3–7
plt.gca().add_patch(patches.FancyArrowPatch(
    (0.20, 0.89), (0.07, 0.70),
    connectionstyle="arc3,rad=.4",
    arrowstyle="Simple, tail_width=1.5, head_width=8, head_length=10",
    color="#444444"))
plt.text(0.12, 0.71, "Seuil\nplus élevé", color="#333333")
plt.xlabel('Taux de Faux Positifs (Chute)')
plt.ylabel('Taux de Vrais Positifs (Rappel)')
plt.grid()
plt.axis([0, 1, 0, 1])
plt.legend(loc="lower right", fontsize=13)

plt.show()

Il est courant de mesurer la surface sous la courbe, représentée par AUC. Plus précisément, la surface sous la courbe ROC. Cela permet de comparer

Attribution : 03_classification.ipynb

Ensemble de données - openml

www.openml.org

OpenML est une plateforme ouverte pour partager des ensembles de données, des algorithmes et des expériences - pour apprendre à mieux apprendre, ensemble.

import numpy as np
np.random.seed(42)

from sklearn.datasets import fetch_openml

diabetes = fetch_openml(name='diabetes', version=1)
print(diabetes.DESCR)

L’ensemble de données d’aujourd’hui est le jeu de données PIMA, qui contient 768 instances et 8 attributs numériques. La nature numérique de ces attributs facilite notre analyse. De plus, étant donné que les données proviennent d’un article publié, elles reflètent probablement une collecte de données soignée, ce qui pourrait conduire à des résultats robustes, car les auteurs auraient eu besoin de données de haute qualité pour soutenir leur publication.

Ensemble de données - openml

Author: Vincent Sigillito

Source: Obtained from UCI

Please cite: UCI citation policy

1. Title: Pima Indians Diabetes Database

2. Sources:

   1. Original owners: National Institute of Diabetes and Digestive and Kidney Diseases
   2. Donor of database: Vincent Sigillito (vgs@aplcen.apl.jhu.edu) Research Center, RMI Group Leader Applied Physics Laboratory The Johns Hopkins University Johns Hopkins Road Laurel, MD 20707 (301) 953-6231
   3. Date received: 9 May 1990

3. Past Usage:

   1. Smith,_J.W., Everhart,_J.E., Dickson,_W.C., Knowler,_W.C., & Johannes,_R.S. (1988). Using the ADAP learning algorithm to forecast the onset of diabetes mellitus. In {it Proceedings of the Symposium on Computer Applications and Medical Care} (pp. 261–265). IEEE Computer Society Press.

      The diagnostic, binary-valued variable investigated is whether the patient shows signs of diabetes according to World Health Organization criteria (i.e., if the 2 hour post-load plasma glucose was at least 200 mg/dl at any survey examination or if found during routine medical care). The population lives near Phoenix, Arizona, USA.

      Results: Their ADAP algorithm makes a real-valued prediction between 0 and 1. This was transformed into a binary decision using a cutoff of 0.448. Using 576 training instances, the sensitivity and specificity of their algorithm was 76% on the remaining 192 instances.

4. Relevant Information: Several constraints were placed on the selection of these instances from a larger database. In particular, all patients here are females at least 21 years old of Pima Indian heritage. ADAP is an adaptive learning routine that generates and executes digital analogs of perceptron-like devices. It is a unique algorithm; see the paper for details.

5. Number of Instances: 768

6. Number of Attributes: 8 plus class

7. For Each Attribute: (all numeric-valued)

   1. Number of times pregnant
   2. Plasma glucose concentration a 2 hours in an oral glucose tolerance test
   3. Diastolic blood pressure (mm Hg)
   4. Triceps skin fold thickness (mm)
   5. 2-Hour serum insulin (mu U/ml)
   6. Body mass index (weight in kg/(height in m)^2)
   7. Diabetes pedigree function
   8. Age (years)
   9. Class variable (0 or 1)

8. Missing Attribute Values: None

9. Class Distribution: (class value 1 is interpreted as “tested positive for diabetes”)

   Class Value Number of instances 0 500 1 268

10. Brief statistical analysis:

    Attribute number: Mean: Standard Deviation:

    1.                 3.8     3.4

    2.               120.9    32.0

    3.                69.1    19.4

    4.                20.5    16.0

    5.                79.8   115.2

    6.                32.0     7.9

    7.                 0.5     0.3

    8.                33.2    11.8

Relabeled values in attribute ‘class’ From: 0 To: tested_negative
From: 1 To: tested_positive

Downloaded from openml.org.

Jeu de données du diabète des Indiens Pima

from sklearn.datasets import fetch_openml

# Charger le jeu de données du diabète des Indiens Pima
pima = fetch_openml(name='diabetes', version=1, as_frame=True)

# Extraire les attributs et la cible
X = pima.data
y = pima.target

# Convertir les étiquettes cibles 'tested_negative' et 'tested_positive' en 0 et 1
y = y.map({'tested_negative': 0, 'tested_positive': 1})

# Diviser le jeu de données
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

Jeu de données du diabète des Indiens Pima tel que décrit dans Knowler et al. (1981) [PubMed].

Comparaison de plusieurs classificateurs

from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier

Comparaison de plusieurs classificateurs

lr = LogisticRegression()
lr.fit(X_train, y_train)

knn = KNeighborsClassifier()
knn.fit(X_train, y_train)

dt = DecisionTreeClassifier()
dt.fit(X_train, y_train)

rf = RandomForestClassifier()
rf.fit(X_train, y_train)

Utilisation des paramètres par défaut.

AUC/ROC

from sklearn.metrics import roc_auc_score

y_pred_prob_lr = lr.predict_proba(X_test)[:, 1]
y_pred_prob_knn = knn.predict_proba(X_test)[:, 1]
y_pred_prob_dt = dt.predict_proba(X_test)[:, 1]
y_pred_prob_rf = rf.predict_proba(X_test)[:, 1]

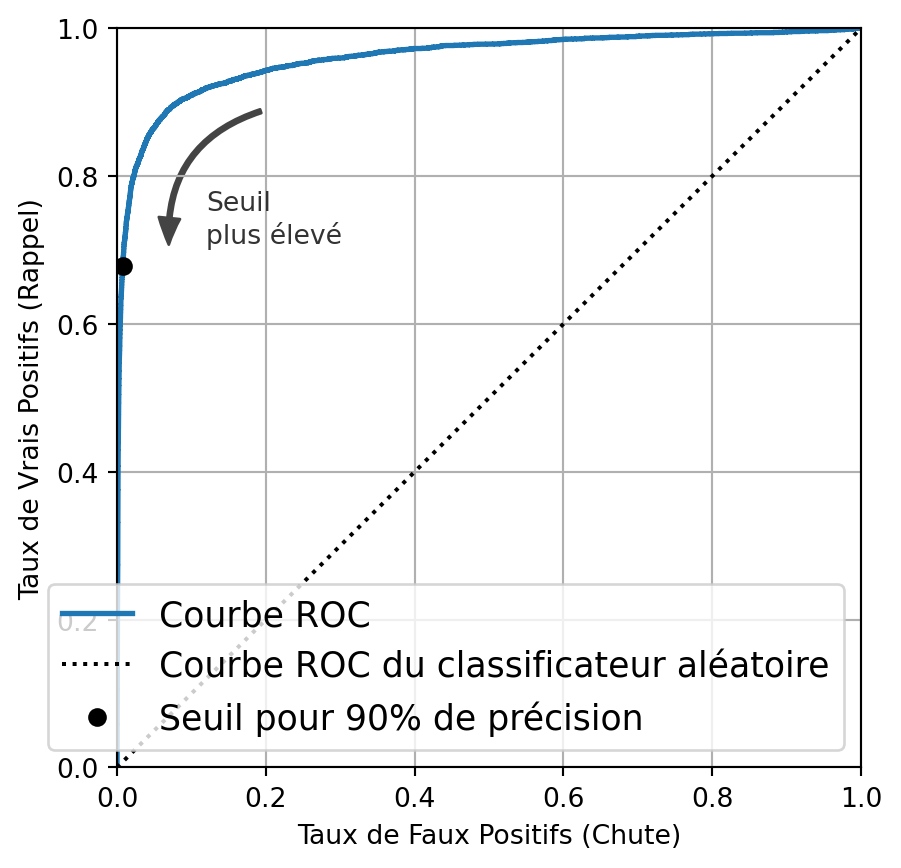
# Calculer les courbes ROC
fpr_lr, tpr_lr, _ = roc_curve(y_test, y_pred_prob_lr)
fpr_knn, tpr_knn, _ = roc_curve(y_test, y_pred_prob_knn)
fpr_dt, tpr_dt, _ = roc_curve(y_test, y_pred_prob_dt)
fpr_rf, tpr_rf, _ = roc_curve(y_test, y_pred_prob_rf)

# Calculer les scores AUC
auc_lr = roc_auc_score(y_test, y_pred_prob_lr)
auc_knn = roc_auc_score(y_test, y_pred_prob_knn)
auc_dt = roc_auc_score(y_test, y_pred_prob_dt)
auc_rf = roc_auc_score(y_test, y_pred_prob_rf)

# Tracer les courbes ROC
plt.figure(figsize=(5, 5)) # plt.figure()
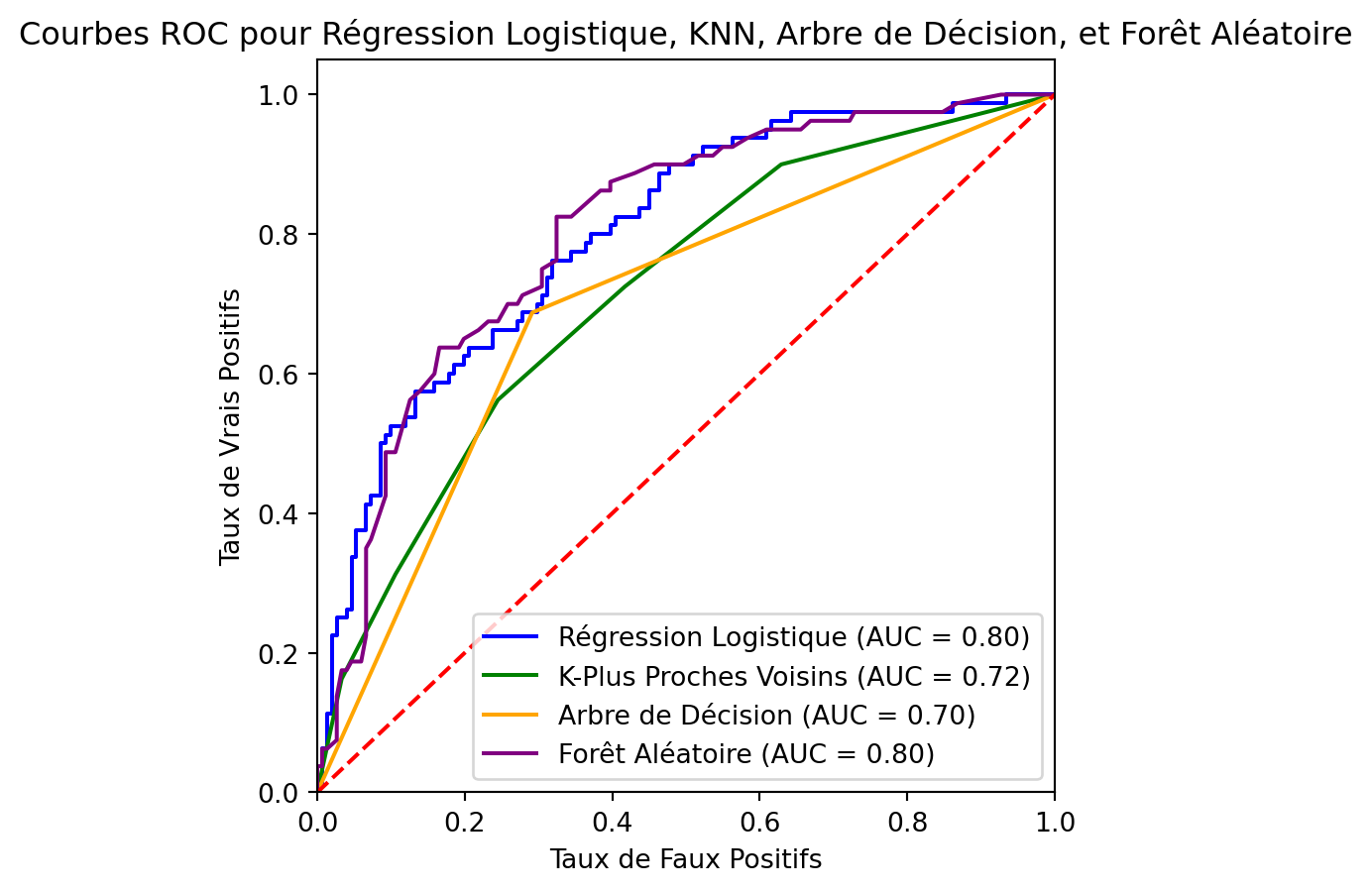
plt.plot(fpr_lr, tpr_lr, color='blue', label=f'Régression Logistique (AUC = {auc_lr:.2f})')
plt.plot(fpr_knn, tpr_knn, color='green', label=f'K-Plus Proches Voisins (AUC = {auc_knn:.2f})')
plt.plot(fpr_dt, tpr_dt, color='orange', label=f'Arbre de Décision (AUC = {auc_dt:.2f})')
plt.plot(fpr_rf, tpr_rf, color='purple', label=f'Forêt Aléatoire (AUC = {auc_rf:.2f})')
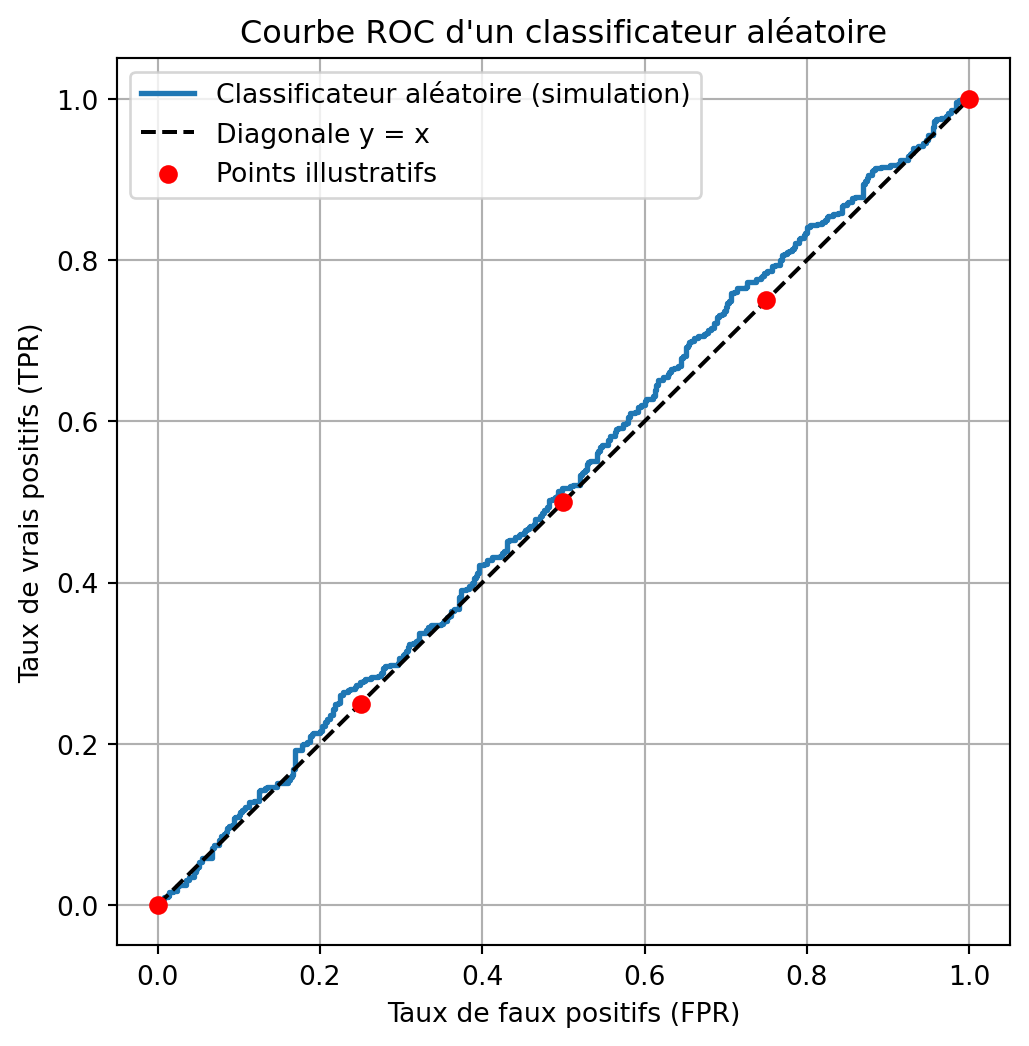
plt.plot([0, 1], [0, 1], color='red', linestyle='--')  # Ligne diagonale pour le hasard
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('Taux de Faux Positifs')
plt.ylabel('Taux de Vrais Positifs')
plt.title('Courbes ROC pour Régression Logistique, KNN, Arbre de Décision, et Forêt Aléatoire')
plt.legend(loc="lower right")
plt.show()

Les courbes ROC fournissent une représentation visuelle de la performance d’un classificateur sur tous les seuils possibles. En traçant le Taux de Vrais Positifs (TPR) contre le Taux de Faux Positifs (FPR), elles permettent aux praticiens d’évaluer le compromis entre sensibilité (rappel) et spécificité.

Contrairement à des métriques telles que la précision, les courbes ROC évaluent la performance du classificateur sans s’appuyer sur un seuil de décision spécifique. Cela les rend particulièrement utiles pour comparer des modèles sur des seuils variables.

Régression logistique

• Modèle :

  \[ h_\theta(x_i) = \sigma(\theta x_i) = \frac{1}{1+e^{- \theta x_i}} \]

• Prédiction :

  • Assigner \(y_i = 0\), si \(h_\theta(x_i) < 0.5\) ; \(y_i = 1\), si \(h_\theta(x_i) \geq 0.5\)

• Fonction de perte : entropie croisée

\[ J(\theta) = - \sum_{i=1}^{N} \left[ y_i \log \sigma(\theta x_i) + (1-y_i) \log (1 - \sigma(\theta x_i)) \right] \]

Le seuil de décision de 0,5 minimse la valeur de la fonction de perte pour le jeu de données d’entraînement.

Les courbes ROC évaluent la performance du classificateur sans s’appuyer sur un seuil de décision spécifique. En fait, ces courbes présentent la variation du TPR en fonction de FPR lorsque l’on fait varié le seuil de décision.

Parcourons ce qui arrive aux termes de la matrice de confusion lorsque le seuil de décision passe de 0 à 1.

Au seuil = 0

• Tous prédits positifs.
• VP : tous les positifs réels sont prédits positifs, VP maximal.
• FP : tous les négatifs réels sont prédits positifs, FP maximal.
• \(\text{TPR} = 1\) (car \(\text{VP} = P\), où \(P\) est le total des positifs).
• \(\text{FPR} = 1\) (car \(\text{FP} = N\), où \(N\) est le total des négatifs).
• Point ROC = \((1,1)\).

À mesure que le seuil augmente de 0 à 1

• Moins d’exemples sont prédits positifs.
• VP diminue (certains positifs ne dépassent plus le seuil).
• FP diminue (certains négatifs ne dépassent plus le seuil).
• TPR diminue de manière monotone de 1 à 0.
• FPR diminue de manière monotone de 1 à 0.
• La courbe trace vers le bas à gauche dans l’espace ROC.

À seuil = 1

• Tous prédits négatifs.
• VP = 0, FP = 0.
• \(\text{TPR} = 0\), \(\text{FPR} = 0\).
• Point ROC = \((0,0)\).

Intuition sommaire

• Seuil plus bas, plus de positifs prédits, VP et FP augmentent, TPR et FPR augmentent.
• Seuil plus haut, plus de négatifs prédits, VP et FP diminuent, TPR et FPR diminuent.
• La forme de la courbe ROC dépend de la capacité de la régression logistique à séparer les positifs des négatifs :
  • Un modèle parfait monte rapidement vers \((0,1)\).
  • Un modèle aléatoire suit la diagonale.
  • Un modèle réaliste se situe entre les deux.

Régression logistique

Ci-dessous se trouve notre implémentation de la régression logistique.

def sigmoid(z):
    """Calcule la fonction sigmoïde."""
    return 1 / (1 + np.exp(-z))

def cost_function(theta, X, y):
    """
    Calcule le coût d'entropie croisée binaire.
    theta : vecteur des paramètres
    X : matrice des attributs (chaque ligne est un exemple)
    y : vraies étiquettes binaires (0 ou 1)
    """
    m = len(y)
    h = sigmoid(X.dot(theta))
    # Ajouter un petit epsilon pour éviter log(0)
    epsilon = 1e-5
    cost = -(1/m) * np.sum(y * np.log(h + epsilon) + (1 - y) * np.log(1 - h + epsilon))
    return cost

def gradient(theta, X, y):
    """Calcule le gradient du coût par rapport à theta."""
    m = len(y)
    h = sigmoid(X.dot(theta))
    return (1/m) * X.T.dot(h - y)

def logistic_regression(X, y, learning_rate=0.1, iterations=1000):
    """
    Entraîne la régression logistique en utilisant la descente de gradient.
    Retourne le vecteur des paramètres optimisés theta et l'historique des valeurs de coût.
    """
    m, n = X.shape
    theta = np.zeros(n)
    cost_history = []
    for i in range(iterations):
        theta -= learning_rate * gradient(theta, X, y)
        cost_history.append(cost_function(theta, X, y))
    return theta, cost_history

def predict_probabilities(theta, X):
    """Retourne les probabilités prédites pour la classe positive."""
    return sigmoid(X.dot(theta))

Implémentation : ROC

def compute_roc_curve(y_true, y_scores, thresholds):
    tpr_list, fpr_list = [], []
    for thresh in thresholds:
        # Classer comme positif si la probabilité prédite >= seuil
        y_pred = (y_scores >= thresh).astype(int)
        TP = np.sum((y_true == 1) & (y_pred == 1))
        FN = np.sum((y_true == 1) & (y_pred == 0))
        FP = np.sum((y_true == 0) & (y_pred == 1))
        TN = np.sum((y_true == 0) & (y_pred == 0))
        TPR = TP / (TP + FN) if (TP + FN) > 0 else 0
        FPR = FP / (FP + TN) if (FP + TN) > 0 else 0
        tpr_list.append(TPR)
        fpr_list.append(FPR)

    tpr_list.reverse()
    fpr_list.reverse()

    return np.array(fpr_list), np.array(tpr_list)

Implémentation : AUC ROC

def compute_auc(fpr, tpr):
    """
    Calcule la Surface Sous la Courbe (AUC) en utilisant la règle des trapèzes.
    
    fpr : tableau des taux de faux positifs
    tpr : tableau des taux de vrais positifs
    """
    return np.trapezoid(tpr, fpr)

La règle des trapèzes (trapezoid), semblable à la somme de Riemann, est une méthode numérique pour approximer l’intégrale définie d’une fonction. En partitionnant l’aire sous la courbe en trapèzes plutôt qu’en rectangles, elle offre généralement une approximation plus précise.

Générer des données + prédictions

# Générer des données synthétiques pour la classification binaire
np.random.seed(seed)
m = 1000  # nombre d'échantillons
X = np.random.randn(m, 2)
noise = 0.5 * np.random.randn(m)

# Définir les étiquettes : une combinaison linéaire bruitée, seuil à 0
y = (X[:, 0] + X[:, 1] + noise > 0).astype(int)

# Ajouter un terme d'interception (une colonne de uns) à X
X_intercept = np.hstack([np.ones((m, 1)), X])

X_train, X_test, y_train, y_test = train_test_split(X_intercept, y, random_state=seed)

# Entraîner un modèle de régression logistique en utilisant la descente de gradient
theta, cost_history = logistic_regression(X_train, y_train, learning_rate=0.1, iterations=1000)

Exemple : tracer

# Calculer les probabilités prédites pour la classe positive sur l'ensemble de test
y_probs = predict_probabilities(theta, X_test)

# Définir un ensemble de valeurs seuils entre 0 et 1 (par exemple, 100 seuils également espacés)
thresholds = np.linspace(0, 1, 100)

# Calculer la courbe ROC (FPR et TPR pour chaque seuil)
fpr, tpr = compute_roc_curve(y_test, y_probs, thresholds)
auc_value = compute_auc(fpr, tpr)

# Tracer la courbe ROC
plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, color='blue', lw=2, label='Courbe ROC (AUC = %0.2f)' % auc_value)
plt.plot([0, 1], [0, 1], color='gray', lw=1, linestyle='--', label='Classificateur aléatoire')
plt.xlabel('Taux de Faux Positifs')
plt.ylabel('Taux de Vrais Positifs')
plt.title('Courbe ROC (Receiver Operating Characteristic)')
plt.legend(loc="lower right")
plt.show()

Classificateur aléatoire (simulation)

rng = np.random.RandomState(42)

# Simuler les étiquettes (ensemble de données équilibré)

y_true = rng.randint(0, 2, size=1000)  # étiquettes réelles aléatoires

# Simuler des scores aléatoires (indépendants des étiquettes)

y_scores = rng.rand(1000)

# Calculer la courbe ROC

fpr, tpr, thresholds = roc_curve(y_true, y_scores)

# Tracer la courbe ROC

plt.figure(figsize=(6,6))
plt.plot(fpr, tpr, label="Classificateur aléatoire (simulation)", lw=2)
plt.plot([0,1],[0,1],'k--', label="Diagonale y = x")
plt.scatter([0,0.25,0.5,0.75,1],[0,0.25,0.5,0.75,1], 
            color="red", zorder=5, label="Points illustratifs")
plt.xlabel("Taux de faux positifs (FPR)")
plt.ylabel("Taux de vrais positifs (TPR)")
plt.title("Courbe ROC d'un classificateur aléatoire")
plt.legend()
plt.grid(True)
plt.show()

Voir aussi

• Receiver Operating Characteristic (ROC) Multiclasse présente des exemples de courbes micro- et macro- moyennes.

La vidéo ci-dessus par StatQuest, Josh Starmer, offre un guide détaillé, étape par étape, sur la façon de construire et d’analyser les courbes ROC (Receiver Operating Characteristic).

Prologue

Résumé

• Examiné les techniques d’évaluation des modèles de classification, en se concentrant sur les matrices de confusion et les métriques clés : précision, exactitude, rappel et score \(F_1\).
• Abordé les limites de la précision dans les ensembles de données déséquilibrés, en introduisant les techniques de moyennage micro et macro.
• Exploré le compromis précision-rappel et l’analyse ROC, y compris la surface sous la courbe (AUC).
• Fournit des perspectives pratiques à travers des implémentations Python.

Sur les mesures de performance

• Sokolova, M. & Lapalme, G. (2009). A systematic analysis of performance measures for classification tasks. Information Processing and Management, 45(4), 427–437.
  • Scopus : 4 793 citations
  • Google Scholar : 7 798 citations

Évaluation des algorithmes d’apprentissage

• Ce livre, avec une note de 4,6 étoiles sur Amazon, explore le processus d’évaluation, en mettant particulièrement l’accent sur les algorithmes de classification (Japkowicz et Shah 2011).

• Nathalie Japkowicz a précédemment été professeure à l’Université d’Ottawa et est actuellement affiliée à l’American University à Washington.

• Mohak Shah, qui a obtenu son doctorat à l’Université d’Ottawa, a occupé de nombreux postes dans l’industrie, y compris Vice-président de l’IA et de l’apprentissage automatique chez LG Electronics.

Prochain cours

• Nous examinerons la validation croisée et le réglage des hyperparamètres.

Références

Géron, Aurélien. 2022. Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow. 3ᵉ éd. O’Reilly Media, Inc.

Japkowicz, Nathalie, et Mohak Shah. 2011. Evaluating Learning Algorithms: a classification perspective. Cambridge: Cambridge University Press.

Knowler, William C., David J. Pettitt, Peter J. Savage, et Peter H. Bennett. 1981. « Diabetes incidence in Pima indians: contributions of obesity and parental diabetes. » American journal of epidemiology 113 2: 144‑56. https://api.semanticscholar.org/CorpusID:25209675.

Russell, Stuart, et Peter Norvig. 2020. Artificial Intelligence: A Modern Approach. 4ᵉ éd. Pearson. http://aima.cs.berkeley.edu/.

Marcel Turcotte

Marcel.Turcotte@uOttawa.ca

École de science informatique et de génie électrique (SIGE)

Université d’Ottawa