Ingénierie de l’apprentissage automatique

CSI 4506 - Automne 2025

Marcel Turcotte

Version: oct. 5, 2025 12h32

Préambule

Message du jour

Objectifs d’apprentissage

  • Expliquer l’extraction de attributs, comparer les méthodes de codage, et justifier les choix en fonction de la nature des données.
  • Appliquer la normalisation/standardisation pour l’échelle des attributs et gérer les valeurs manquantes par imputation.
  • Définir le déséquilibre des classes, explorer des solutions comme le rééchantillonnage et SMOTE, et garantir une application appropriée.
  • Appliquer les concepts à des ensembles de données du monde réel, analyser les résultats, et comprendre le pipeline d’apprentissage automatique.
  • Reconnaître l’impact de la taille de l’ensemble de données, discuter de l’augmentation des données, et explorer l’efficacité des données dans l’apprentissage automatique.

L’ingénierie de l’apprentissage automatique

Ingénierie de l’apprentissage automatique

Encodage

Pourquoi?

Après avoir complété le devoir 1, vous avez généré un fichier .csv contenant des données nettoyées.

Pourquoi des étapes supplémentaires seraient nécessaires?

Données - Adult

import numpy as np
np.random.seed(42)

from sklearn.datasets import fetch_openml

adult = fetch_openml(name='adult', version=2)

print(adult.DESCR)

Données - Adult

Author: Ronny Kohavi and Barry Becker
Source: UCI - 1996
Please cite: Ron Kohavi, “Scaling Up the Accuracy of Naive-Bayes Classifiers: a Decision-Tree Hybrid”, Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, 1996

Prediction task is to determine whether a person makes over 50K a year. Extraction was done by Barry Becker from the 1994 Census database. A set of reasonably clean records was extracted using the following conditions: ((AAGE>16) && (AGI>100) && (AFNLWGT>1)&& (HRSWK>0))

This is the original version from the UCI repository, with training and test sets merged.

Variable description

Variables are all self-explanatory except fnlwgt. This is a proxy for the demographic background of the people: “People with similar demographic characteristics should have similar weights”. This similarity-statement is not transferable across the 51 different states.

Description from the donor of the database:

The weights on the CPS files are controlled to independent estimates of the civilian noninstitutional population of the US. These are prepared monthly for us by Population Division here at the Census Bureau. We use 3 sets of controls. These are: 1. A single cell estimate of the population 16+ for each state. 2. Controls for Hispanic Origin by age and sex. 3. Controls by Race, age and sex.

We use all three sets of controls in our weighting program and “rake” through them 6 times so that by the end we come back to all the controls we used. The term estimate refers to population totals derived from CPS by creating “weighted tallies” of any specified socio-economic characteristics of the population. People with similar demographic characteristics should have similar weights. There is one important caveat to remember about this statement. That is that since the CPS sample is actually a collection of 51 state samples, each with its own probability of selection, the statement only applies within state.

Relevant papers

Ronny Kohavi and Barry Becker. Data Mining and Visualization, Silicon Graphics.
e-mail: ronnyk ‘@’ live.com for questions.

Downloaded from openml.org.

Adult - Workclass

adult.data['workclass'].unique()
['Private', 'Local-gov', NaN, 'Self-emp-not-inc', 'Federal-gov', 'State-gov', 'Self-emp-inc', 'Without-pay', 'Never-worked']
Categories (8, object): ['Federal-gov', 'Local-gov', 'Never-worked', 'Private', 'Self-emp-inc', 'Self-emp-not-inc', 'State-gov', 'Without-pay']

Adult - Education

adult.data['education'].unique()
['11th', 'HS-grad', 'Assoc-acdm', 'Some-college', '10th', ..., 'Assoc-voc', '9th', '12th', '1st-4th', 'Preschool']
Length: 16
Categories (16, object): ['10th', '11th', '12th', '1st-4th', ..., 'Masters', 'Preschool', 'Prof-school', 'Some-college']

Adult - Marital Status

adult.data['marital-status'].unique()
['Never-married', 'Married-civ-spouse', 'Widowed', 'Divorced', 'Separated', 'Married-spouse-absent', 'Married-AF-spouse']
Categories (7, object): ['Divorced', 'Married-AF-spouse', 'Married-civ-spouse', 'Married-spouse-absent', 'Never-married', 'Separated', 'Widowed']

Données catégorielles

Points clés sur la représentation des données

  • Représentation numérique: Certains algorithmes d’apprentissage nécessitent que les données soient sous forme numérique.

Méthodes d’encodage

Considérons l’attribut workclass, qui a 8 valeurs distinctes telles que ‘Federal-gov’, ‘Local-gov’, etc.

  • Quelle méthode d’encodage est préférable et pourquoi?
  1. w = 1, 2, 3, 4, 5, 6, 7, ou 8
  2. w = [0,0,0], [0,0,1], [0,1,0], \(\ldots\), ou [1,1,1]
  3. w = [1,0,0,0,0,0,0,0], [0,1,0,0,0,0,0,0], \(\ldots\), ou [0,0,0,0,0,0,0,1]

Encodage pour les données catégorielles

Encodage One-Hot: Cette méthode est à privilégier pour les données catégorielles.

  • Augmente la dimensionnalité: L’encodage One-Hot augmente la dimensionnalité des vecteurs de attributs.
  • Évite les biais: Les autres méthodes d’encodage peuvent introduire des biais.
  • Exemple de biais: En utilisant la première méthode, w = 1, 2, 3, etc., cela implique que ‘Federal-gov’ et ‘Local-gov’ sont similaires, tandis que ‘Federal-gov’ et ‘Without-pay’ ne le sont pas.
  • Similitude trompeuse: La deuxième méthode, w = [0,0,0], [0,0,1], etc., pourrait induire en erreur l’algorithme en suggérant une similarité basée sur des schémas numériques.

Définition

Encodage One-Hot: Une technique qui convertit les variables catégorielles en une représentation vectorielle binaire, où chaque catégorie est représentée par un vecteur avec un seul ‘1’ et tous les autres éléments à ‘0’.

OneHotEncoder

from numpy import array
from sklearn.preprocessing import OneHotEncoder

work = adult.data[['workclass']]

onehot_encoder = OneHotEncoder()

onehot_encoder.fit(work)
values_encoded = onehot_encoder.transform(work)

for i in range(5): print(values_encoded.toarray()[i])
[0. 0. 0. 1. 0. 0. 0. 0. 0.]
[0. 0. 0. 1. 0. 0. 0. 0. 0.]
[0. 1. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 1. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 1.]

Étude de cas

  • Ensemble de données : Heart Disease
    • Exemples : 303, Attributs : 13, Cible : Présence/absence de maladie
  • Données catégorielles :
    • sexe : 1 = homme, 0 = femme
    • cp (type de douleur thoracique) :
      • 1 : Angine typique
      • 2 : Angine atypique
      • 3 : Douleur non angineuse
      • 4 : Asymptomatique
    • Autres : ‘fbs’, ‘restecg’, ‘exang’, ‘slope’, ‘thal’

Étude de cas

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_openml
from sklearn.preprocessing import OneHotEncoder, StandardScaler
from sklearn.compose import ColumnTransformer
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report

# Chargement de l'ensemble de données 'Heart-Disease' depuis OpenML
data = fetch_openml(name='Heart-Disease', version=1, as_frame=True)
df = data.frame

# Remplacer '?' par NaN et convertir les colonnes en numérique
for col in df.columns:
    df[col] = pd.to_numeric(df[col], errors='coerce')

# Supprimer les lignes avec des valeurs manquantes
df.dropna(inplace=True)

# Définir les attributs et la cible
X = df.drop(columns=['target'])
y = df['target']

# Colonnes à encoder avec OneHotEncoder
colonnes_a_encoder = ['sex', 'cp', 'fbs', 'restecg', 'exang', 'slope', 'thal']

# Identifier les colonnes numériques
colonnes_numeriques = X.columns.difference(colonnes_a_encoder)

# Diviser l'ensemble de données en ensembles d'entraînement et de test avant les transformations
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=42
)

# Appliquer OneHotEncoder et StandardScaler à l'aide de ColumnTransformer
column_transformer = ColumnTransformer(
    transformers=[
        ('onehot', OneHotEncoder(), colonnes_a_encoder),
        ('scaler', StandardScaler(), colonnes_numeriques)
    ]
)

# Ajuster le transformateur sur les données d'entraînement et transformer les données d'entraînement et de test
X_train_processed = column_transformer.fit_transform(X_train)
X_test_processed = column_transformer.transform(X_test)

# Initialiser et entraîner le modèle de régression logistique
model = LogisticRegression(max_iter=1000)
model = model.fit(X_train_processed, y_train)

Étude de cas - résultats

# Prédire et évaluer le modèle
y_pred = model.predict(X_test_processed)

print(classification_report(y_test, y_pred))
              precision    recall  f1-score   support

         0.0       0.87      0.93      0.90        29
         1.0       0.93      0.88      0.90        32

    accuracy                           0.90        61
   macro avg       0.90      0.90      0.90        61
weighted avg       0.90      0.90      0.90        61

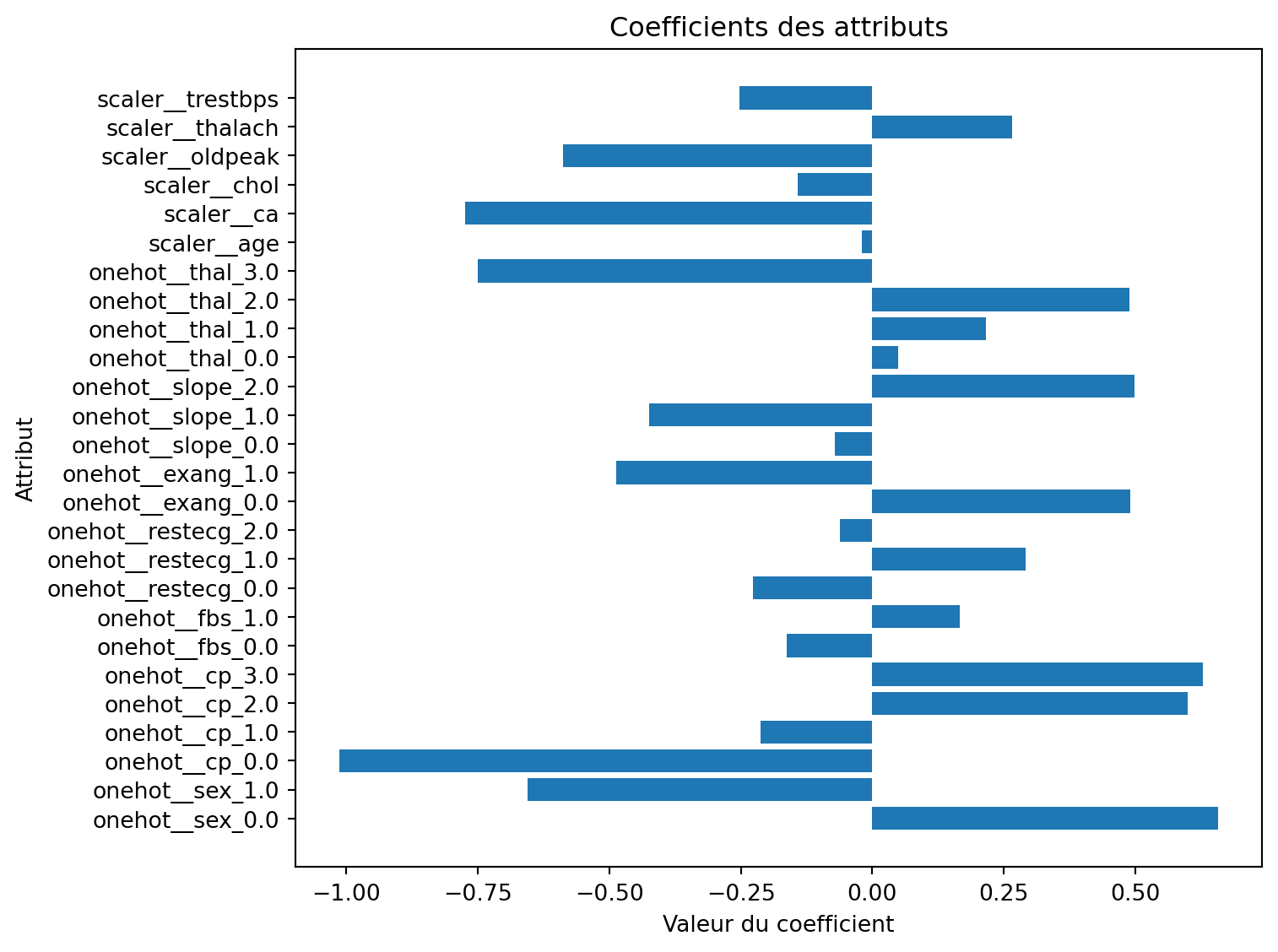
Étude de cas - douleur thoracique (cp)

# Récupérer les noms des attributs après transformation à l'aide de get_feature_names_out()
feature_names = column_transformer.get_feature_names_out()

# Obtenir les coefficients et les associer aux noms des attributs
coefficients = model.coef_[0]

# Créer un DataFrame avec les noms des attributs et les coefficients
coef_df = pd.DataFrame({
    'Attribut': feature_names,
    'Coefficient': coefficients
})

# Afficher les coefficients associés à 'cp'
cp_features = coef_df[coef_df['Attribut'].str.contains('_cp')]
print("\nCoefficients associés à 'cp' :")
print(cp_features)

Coefficients associés à 'cp' :
         Attribut  Coefficient
2  onehot__cp_0.0    -1.013382
3  onehot__cp_1.0    -0.212284
4  onehot__cp_2.0     0.599934
5  onehot__cp_3.0     0.628824

Étude de cas - coefficients

# Visualiser les coefficients

plt.figure(figsize=(8, 6))
plt.barh(coef_df['Attribut'], coef_df['Coefficient'])
plt.title('Coefficients des attributs')
plt.xlabel('Valeur du coefficient')
plt.ylabel('Attribut')
plt.tight_layout()
plt.show()

Étude de cas - coefficients

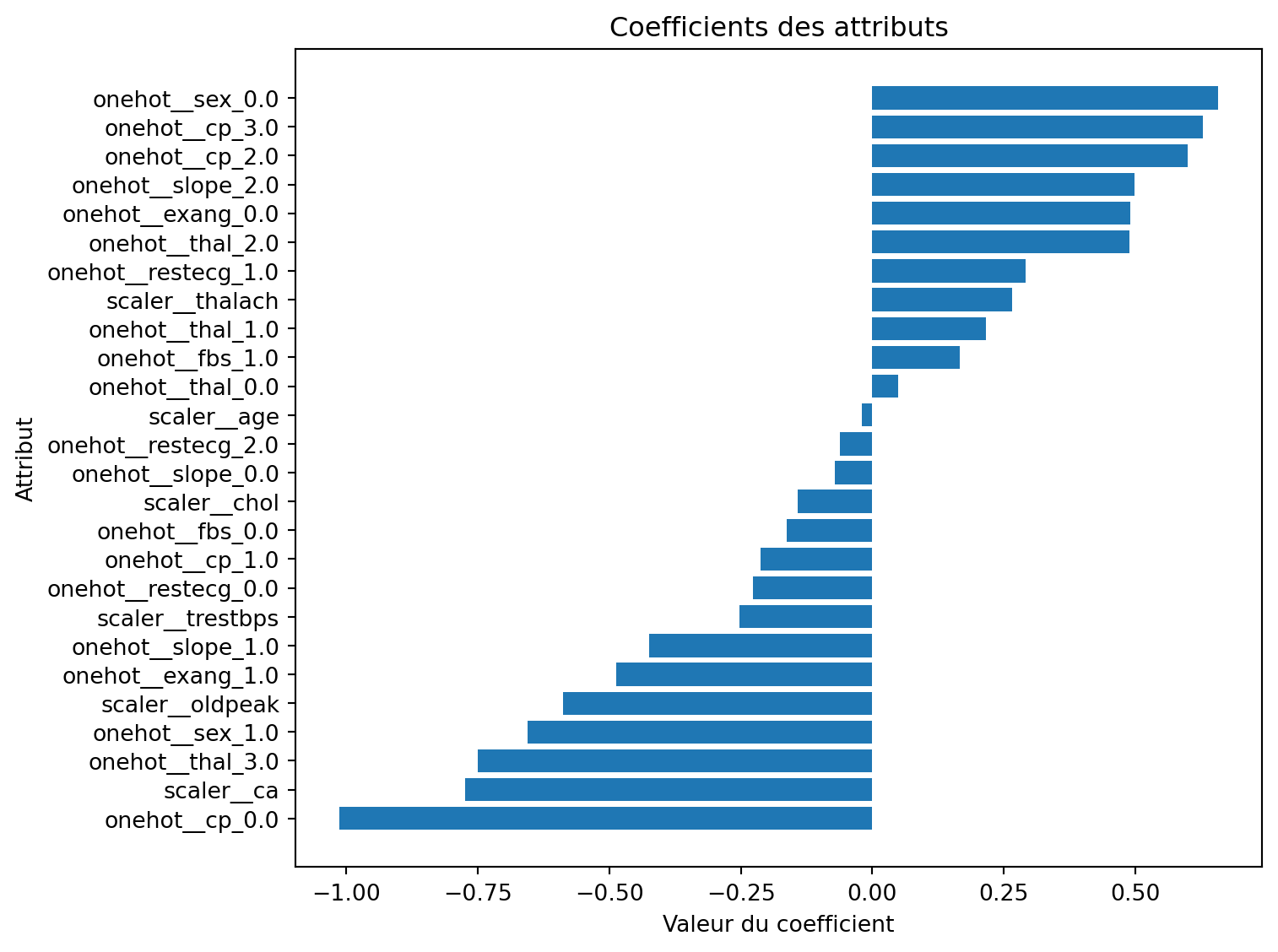
Étude de cas - coefficients (triés)

# Visualiser les coefficients

plt.figure(figsize=(8, 6))
coef_df.sort_values(by='Coefficient', inplace=True)
plt.barh(coef_df['Attribut'], coef_df['Coefficient'])
plt.title('Coefficients des attributs')
plt.xlabel('Valeur du coefficient')
plt.ylabel('Attribut')
plt.tight_layout()
plt.show()

Étude de cas - coefficients (triés)

Définition

L’encodage ordinal est une technique qui attribue des valeurs numériques aux attributs catégoriels en fonction de leur ordre ou de leur classement intrinsèque.

Encodage ordinal

Pour les attributs avec des valeurs comme ‘Mauvais’, ‘Moyen’, et ‘Bon’, un encodage ordinal aurait du sens.

Cependant !

from numpy import array
from sklearn.preprocessing import OrdinalEncoder

X =[['Mauvais'], ['Moyen'], ['Bon'], ['Moyen'], ['Moyen']]

encoder = OrdinalEncoder()

encoder.fit(X)
encoder.transform(X)
array([[1.],
       [2.],
       [0.],
       [2.],
       [2.]])

OrdinalEncoder (révisé)

from numpy import array
from sklearn.preprocessing import OrdinalEncoder

X =[['Mauvais'], ['Moyen'], ['Bon'], ['Moyen'], ['Moyen']]

encoder = OrdinalEncoder(categories=[['Mauvais', 'Moyen', 'Bon']])

encoder.fit(X)

X_encoded = encoder.transform(X)

X_encoded
array([[0.],
       [1.],
       [2.],
       [1.],
       [1.]])

Définition

La discrétisation consiste à regrouper des valeurs ordinales en catégories discrètes.

Ingénierie des attributs : Binning

Exemple : Catégoriser les âges en groupes tels que ‘nourrisson’, ‘enfant’, ‘adolescent’, ‘adulte’, et ‘senior’.

Avantages :

  • Permet à l’algorithme d’apprendre efficacement avec moins d’exemples d’entraînement.

Inconvénients :

  • Nécessite une expertise dans le domaine pour définir des catégories significatives.
  • Peut manquer de généralisabilité ; par exemple, l’âge de départ pour ‘senior’ pourrait être 60, 65 ou 701.

FunctionTransformer

import pandas as pd
import numpy as np
from sklearn.preprocessing import FunctionTransformer

bins = [0, 1, 13, 20, 60, np.inf]
labels = ['nourrisson', 'enfant', 'adolescent', 'adulte', 'senior']

transformer = FunctionTransformer(
    pd.cut, kw_args={'bins': bins, 'labels': labels, 'retbins': False}
)

X = np.array([0.5, 2, 15, 25, 97])
transformer.fit_transform(X)
['nourrisson', 'enfant', 'adolescent', 'adulte', 'senior']
Categories (5, object): ['nourrisson' < 'enfant' < 'adolescent' < 'adulte' < 'senior']

Mise à l’échelle

Qu’est-ce que c’est ?

Mettre à l’échelle les attributs garantit que leurs valeurs se situent dans des plages comparables.

Pourquoi ?

Pourquoi la mise à l’échelle des données est-elle une bonne pratique ?

Scénario

Nous prétendons prédire le prix d’une maison en utilisant la régression par les k-plus proches voisins (KNN) avec deux attributs :

  • \(x_1\) : nombre de pièces (petite échelle)
  • \(x_2\) : superficie en pieds carrés (grande échelle)

Données (trois maisons)

import numpy as np
import pandas as pd

# Trois exemples (pièces, sqft); prix seulement pour b et c (entraînement)
point_names = ["a", "b", "c"]
X = np.array([
    [4, 1500.0],  # a (requête)
    [8, 1520.0],  # b (entraînement)
    [4, 1300.0],  # c (entraînement)
], dtype=float)

prices = pd.Series([np.nan, 520_000, 390_000], index=point_names, name="price")

df = pd.DataFrame(X, columns=["rooms", "sqft"], index=point_names)
display(df)
display(prices.to_frame())

Remarque. Nous considérerons b et c comme l’ensemble d’entraînement, et a comme la requête dont nous voulons prédire le prix.

Données (trois maisons)

rooms sqft
a 4.0 1500.0
b 8.0 1520.0
c 4.0 1300.0
price
a NaN
b 520000.0
c 390000.0

Distances euclidiennes (non mises à l’échelle)

Lorsqu’un attribut a une échelle beaucoup plus grande (par exemple, la superficie en pieds carrés), elle peut dominer la somme.

from sklearn.metrics import pairwise_distances

dist_unscaled = pd.DataFrame(
    pairwise_distances(df.values, metric="euclidean"),
    index=df.index, columns=df.index
)
dist_unscaled
print("Le plus proche de 'a' (non mis à l'échelle) :", dist_unscaled.loc["a"].drop("a").idxmin())
Le plus proche de 'a' (non mis à l'échelle) : b

Distances euclidiennes (non mises à l’échelle)

a b c
a 0.000000 20.396078 200.000000
b 20.396078 0.000000 220.036361
c 200.000000 220.036361 0.000000

Mise à l’échelle appropriée pour la modélisation

Pour un flux de travail ML équitable, calculez les paramètres d’échelle sur les données d’entraînement (b, c) uniquement, puis transformez à la fois l’entraînement et la requête :

from sklearn.preprocessing import StandardScaler

train_idx = ["b", "c"]
query_idx = ["a"]

scaler = StandardScaler()

scaler.fit(df.loc[train_idx])     # ajuster uniquement sur les points d'entraînement

Z = pd.DataFrame(
    scaler.transform(df),
    columns=df.columns, index=df.index
)

Z

Mise à l’échelle appropriée pour la modélisation

rooms sqft
a -1.0 0.818182
b 1.0 1.000000
c -1.0 -1.000000

Distances euclidiennes (après mise à l’échelle)

dist_scaled = pd.DataFrame(
    pairwise_distances(Z.values, metric="euclidean"),
    index=Z.index, columns=Z.index
)
dist_scaled
a b c
a 0.000000 2.008247 1.818182
b 2.008247 0.000000 2.828427
c 1.818182 2.828427 0.000000 
print("Le plus proche de 'a' (mis à l'échelle):", dist_scaled.loc["a"].drop("a").idxmin())
Le plus proche de 'a' (mis à l'échelle): c

Régression KNN

Nous allons exécuter un régressseur 1-NN (donc la prédiction est exactement le prix du plus proche voisin) avec et sans mise à l’échelle.

from sklearn.neighbors import KNeighborsRegressor
from sklearn.pipeline import Pipeline

X_train = df.loc[train_idx].values          # b, c
y_train = prices.loc[train_idx].values      # prix pour b, c
X_query = df.loc[query_idx].values          # a

Régression KNN (sans mise à l’échelle)

# 1) Sans mise à l'échelle

knn_plain = KNeighborsRegressor(n_neighbors=1, metric="euclidean")

knn_plain.fit(X_train, y_train)

pred_plain = knn_plain.predict(X_query)[0]

Régression KNN (avec mise à l’échelle)

# 2) Avec mise à l'échelle (le pipeline ajuste le scaler uniquement sur les données d'entraînement, puis KNN sur les données mises à l'échelle)

knn_scaled = Pipeline([
    ("scaler", StandardScaler()),
    ("knn", KNeighborsRegressor(n_neighbors=1, metric="euclidean"))
])

knn_scaled.fit(X_train, y_train)

pred_scaled = knn_scaled.predict(X_query)[0]

Régression KNN (résultats)

pd.DataFrame(
    {
        "prédiction (sans mise à l'échelle)": [pred_plain],
        "prédiction (avec mise à l'échelle)": [pred_scaled],
        "plus proche voisin (sans mise à l'échelle)": [point_names[1] if pred_plain==prices['b'] else point_names[2]],
        "plus proche voisin (avec mise à l'échelle)": [point_names[1] if pred_scaled==prices['b'] else point_names[2]],
    },
    index=["a"]
)
prédiction (sans mise à l'échelle) prédiction (avec mise à l'échelle) plus proche voisin (sans mise à l'échelle) plus proche voisin (avec mise à l'échelle)
a 520000.0 390000.0 b c

Normalisation

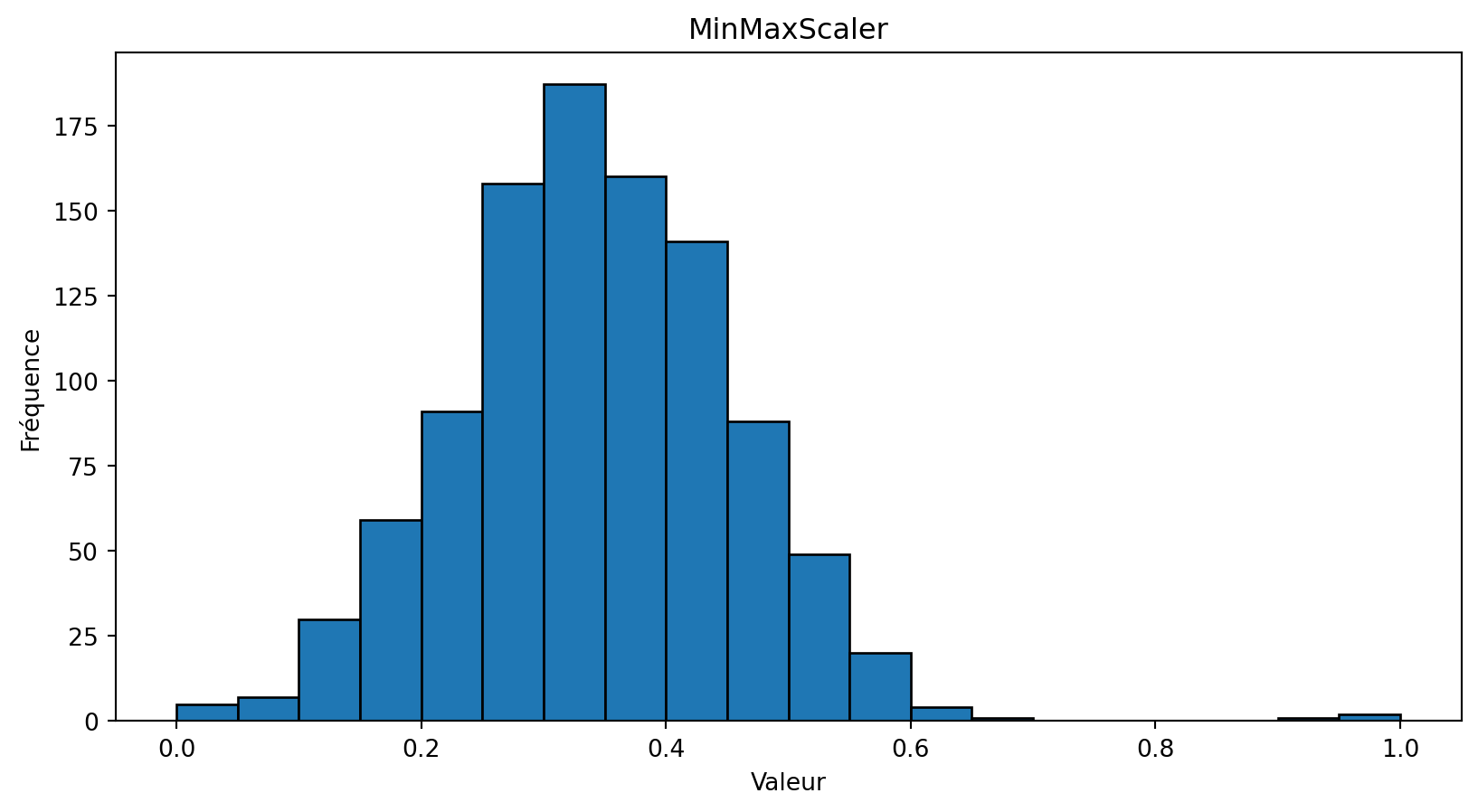
Les algorithmes d’apprentissage fonctionnent de manière optimale lorsque les valeurs des attributs ont des plages similaires, telles que [-1,1] ou [0,1].

  • Cela accélère l’optimisation (par exemple, descente de gradient).

Normalisation: \[ \frac{x_i^{(j)} - \min^{(j)}}{\max^{(j)} - \min^{(j)}} \]

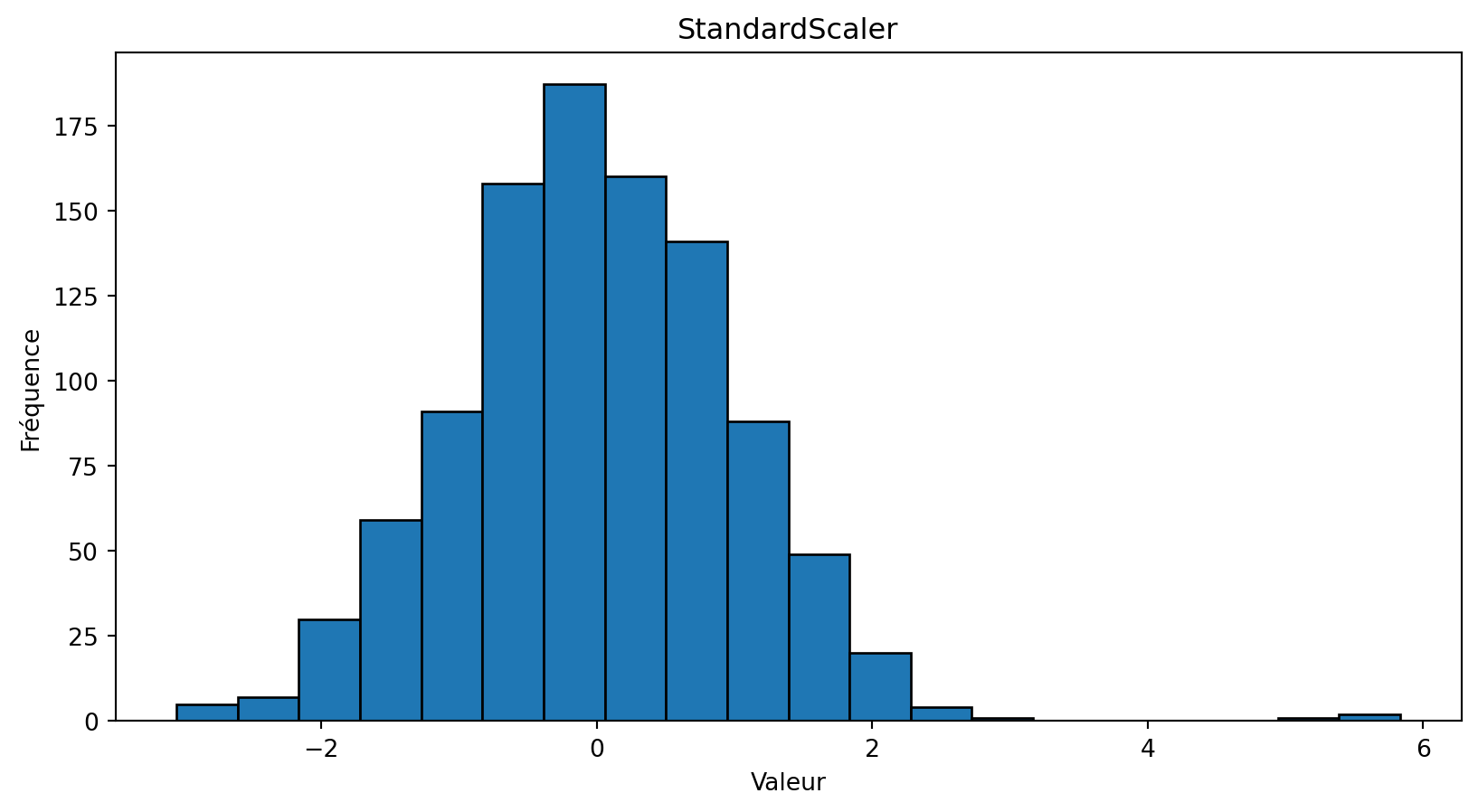
Standardisation

La standardisation (également appelée normalisation par score-z) transforme chaque attribut pour qu’elle ait une distribution normale avec une moyenne (\(\mu\)) de 0 et un écart type (\(\sigma\)) de 1.

\[ \frac{x_i^{(j)} - \mu^{(j)}}{\sigma^{(j)}} \]

Remarque : Les valeurs ne sont pas bornées !

Standardisation ou normalisation ?

  • Traitez la mise à l’échelle comme un hyperparamètre et évaluez à la fois normalisation et standardisation.
  • La standardisation est généralement plus robuste aux valeurs aberrantes (outliers) que la normalisation.
  • Directives de Andriy Burkov (2019), § 5 :
    • Utilisez la standardisation si les attributs sont approximativement distribuées normalement.
    • Préférez la standardisation en présence de valeurs aberrantes.
    • Sinon, utilisez la normalisation.
Caractéristique Standardisation Normalisation
Plage de sortie Non bornée Typiquement [0, 1]
Centre Moyenne à 0 Non centrée
Sensibilité aux valeurs aberrantes Faible Élevée
Cas d’utilisation principal Choix par défaut ; pour les modèles supposant des données centrées sur zéro Lorsque des entrées bornées sont requises (par exemple, traitement d’image, certains réseaux neuronaux)

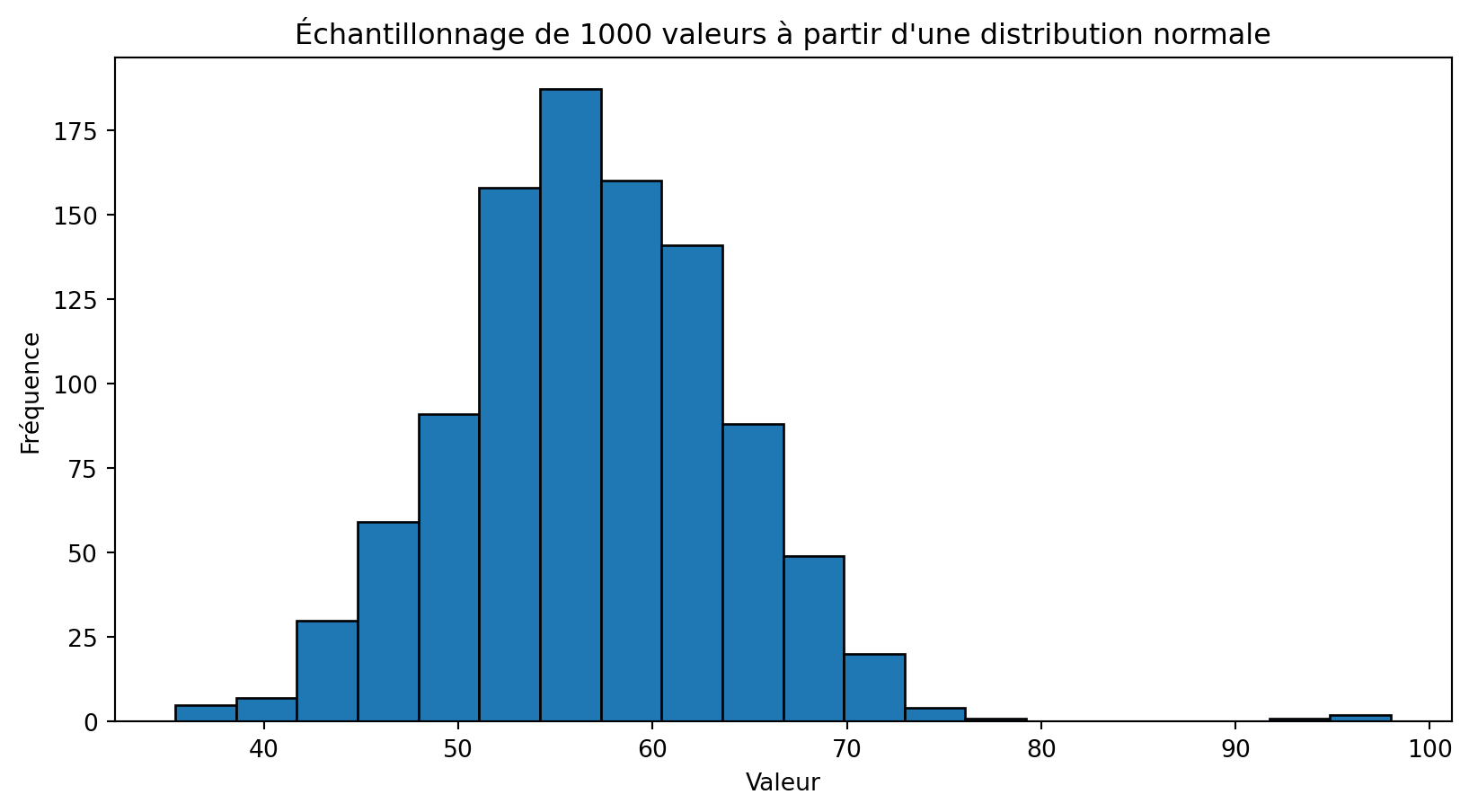
Étude de cas - distribution normale

import numpy as np
np.random.seed(7)

# Charactéristiques de l'échantillon

sample_size = 1000
mu = 57
sigma = 7

# Générer des valeurs

norm_values = sigma * np.random.randn(sample_size) + mu

# Ajout de trois valeurs aberrantes

norm_values = np.append(norm_values, [92, 95, 98])

Étude de cas - distribution normale

Normalisation

Standardisation

Évitez la fuite de données !

Le flux de travail correct :

  • Divisez vos données en un ensemble d’entraînement et un ensemble de test.
  • Ajustez votre standardiseur (par exemple, StandardScaler) sur les données d’entraînement (scaler.fit(X_train)).
    • Cette étape apprend la moyenne et l’écart type des données d’entraînement.
  • Transformez à la fois les données d’entraînement (scaler.transform(X_train)) et les données de test (scaler.transform(X_test)) en utilisant le standardiseur qui a été ajusté sur les données d’entraînement.

Valeurs manquantes

Définition

Les valeurs manquantes font référence à l’absence de données ou de valeurs dans un ensemble de données là où une valeur est attendue.

Gestion des valeurs manquantes

  • Supprimer les exemples:
    • Faisable si l’ensemble de données est grand et que l’issue n’est pas affectée.
  • Supprimer les attributs :
    • Convient si cela n’affecte pas le résultat du projet.
  • Utiliser des algorithmes qui gèrent les données manquantes :
    • Exemple : XGBoost
    • Remarque : Certains algorithmes comme sklearn.linear_model.LinearRegression ne peuvent pas traiter les valeurs manquantes.
  • Imputation des données :
    • Remplacer les valeurs manquantes par des valeurs calculées.

Définition

L’imputation des données est le processus consistant à remplacer les valeurs manquantes dans un ensemble de données par des valeurs substituées, généralement en utilisant des méthodes statistiques ou d’apprentissage automatique.

Stratégie d’imputation des données

Remplacer les valeurs manquantes par la moyenne ou la médiane de l’attribut.

from sklearn.impute import SimpleImputer

imputer = SimpleImputer(strategy="median")

X = imputer.fit_transform(X)

  • Inconvénients : Ignore les corrélations entre les attributs et les relations complexes.

  • Imputation par la mode : Remplacer les valeurs manquantes par la valeur la plus fréquente ; ignore également les corrélations entre les attributs.

Stratégie d’imputation des données

Méthode de valeur spéciale : Remplacer les valeurs manquantes par une valeur en dehors de la plage normale (par exemple, utiliser -1 ou 2 pour des données normalisées entre [0,1]).

  • Objectif : Permettre à l’algorithme d’apprentissage de reconnaître et de gérer correctement les valeurs manquantes.

Approche alternative

  • Définition du problème : Prédire des étiquettes inconnues (manquantes) pour des exemples donnés.
  • Avez-vous déjà rencontré ce type de problème auparavant ?
  • Pertinence : Cela peut être formulé comme un problème d’apprentissage supervisé.
    • Soit \(\hat{x_i}\) un nouvel exemple : \([x_i^{(1)}, x_i^{(2)}, \ldots, x_i^{(j-1)}, x_i^{(j+1)}, \ldots, x_i^{(D)}]\).
    • Soit \(\hat{y}_i = x_i^{j}\).
    • Ensemble d’entraînement : Utiliser des exemples où \(x_i^{j}\) n’est pas manquant.
    • Méthode : Entraîner un classificateur sur cet ensemble pour prédire (imputer) les valeurs manquantes.

Utiliser l’apprentissage automatique pour l’imputation

  1. Méthode basée sur les instances :

    • Utiliser \(k\) plus proches voisins (k-NN) pour trouver les \(k\) exemples les plus proches et imputer à l’aide des valeurs non manquantes du voisinage.

  2. Méthodes basées sur des modèles :

    • Utiliser des techniques avancées telles que les forêts aléatoires, la décomposition tensorielle ou les réseaux neuronaux profonds.

Pourquoi utiliser ces méthodes ?

  • Avantages :
    • Traitent efficacement les relations complexes et les corrélations entre les attributs.
  • Inconvénients :
    • Coût-intensif en termes de temps de travail, de CPU et de ressources mémoire.

Déséquilibre des classes

Définition

Le problème de déséquilibre des classes (class imbalance) survient lorsqu’un grand nombre d’exemples appartient à une classe majoritaire, tandis qu’un nombre relativement faible d’exemples appartient à une ou plusieurs classes minoritaires.

Les modèles ont tendance à favoriser la classe majoritaire, ce qui conduit à de mauvaises performances sur la classe minoritaire.

Solutions

  • Rééchantillonnage :
    • Techniques comme le suréchantillonnage de la classe minoritaire ou le sous-échantillonnage de la classe majoritaire.
  • Ajustements algorithmiques :

    • Utiliser l’apprentissage sensible aux coûts ou ajuster les seuils de décision.

  • Données synthétiques :
    • Générer des exemples synthétiques pour la classe minoritaire en utilisant des méthodes comme SMOTE (Synthetic Minority Over-sampling Technique).

Appliquer les solutions uniquement à l’ensemble d’entraînement pour éviter les fuites de données!

Nouveaux attributs

Définition

L’ingénierie des attributs est le processus de création, transformation et sélection de variables (attributs) à partir de données brutes pour améliorer la performance des modèles d’apprentissage automatique.

Exploration

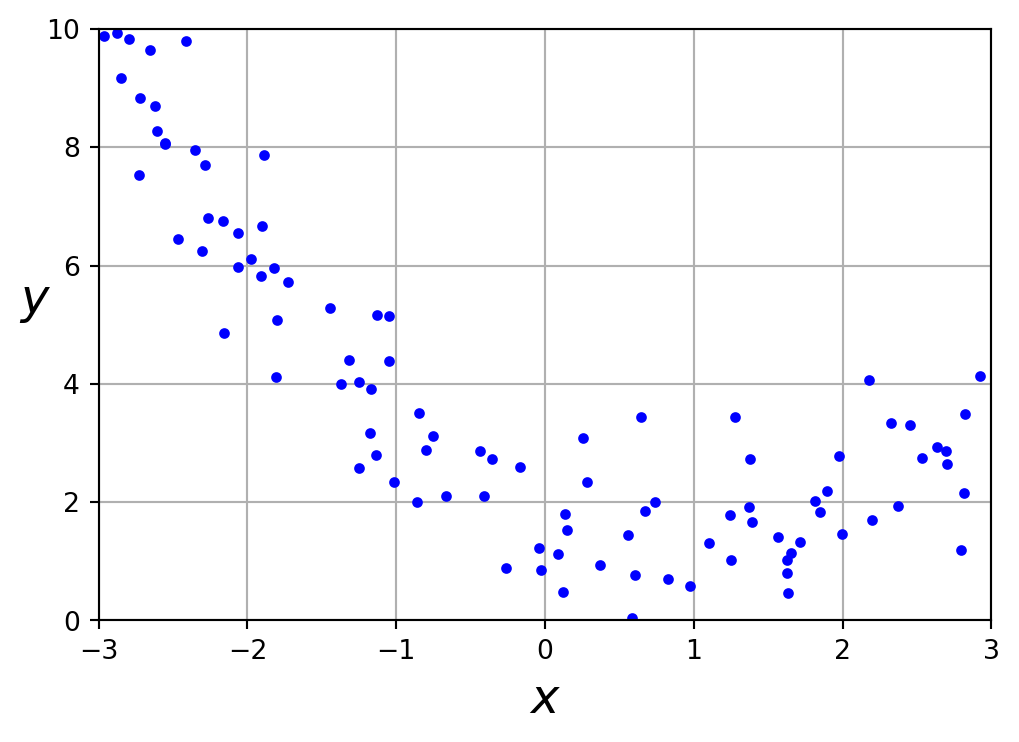
Code 
import numpy as np

np.random.seed(42)

X = 6 * np.random.rand(100, 1) - 3
y = 0.5 * X ** 2 - X + 2 + np.random.randn(100, 1)

import matplotlib as mpl
import matplotlib.pyplot as plt

plt.figure(figsize=(6,4))

plt.plot(X, y, "b.")
plt.xlabel("$x$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([-3, 3, 0, 10])
plt.grid(True)
plt.show()

Régression linéaire

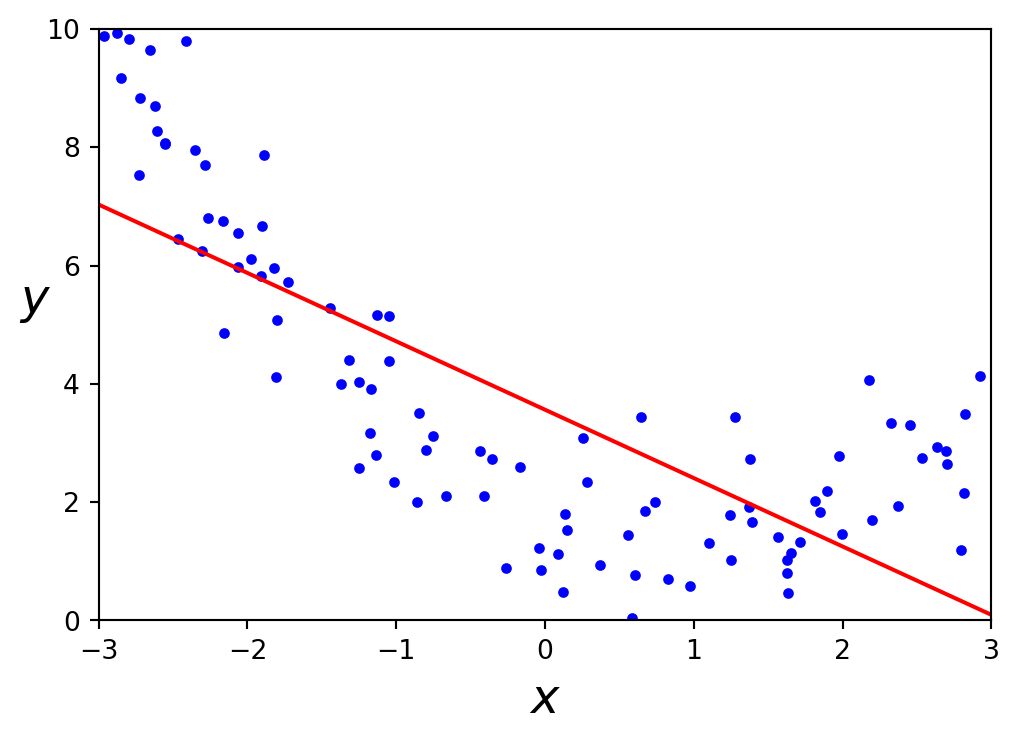
Code 
from sklearn.linear_model import LinearRegression

lin_reg = LinearRegression()
lin_reg.fit(X, y)

X_new = np.array([[-3], [3]])
y_pred = lin_reg.predict(X_new)

plt.figure(figsize=(6,4))

plt.plot(X, y, "b.")
plt.plot(X_new, y_pred, "r-")
plt.xlabel("$x$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([-3, 3, 0, 10])
plt.show()

Un modèle linéaire représente mal ces données.

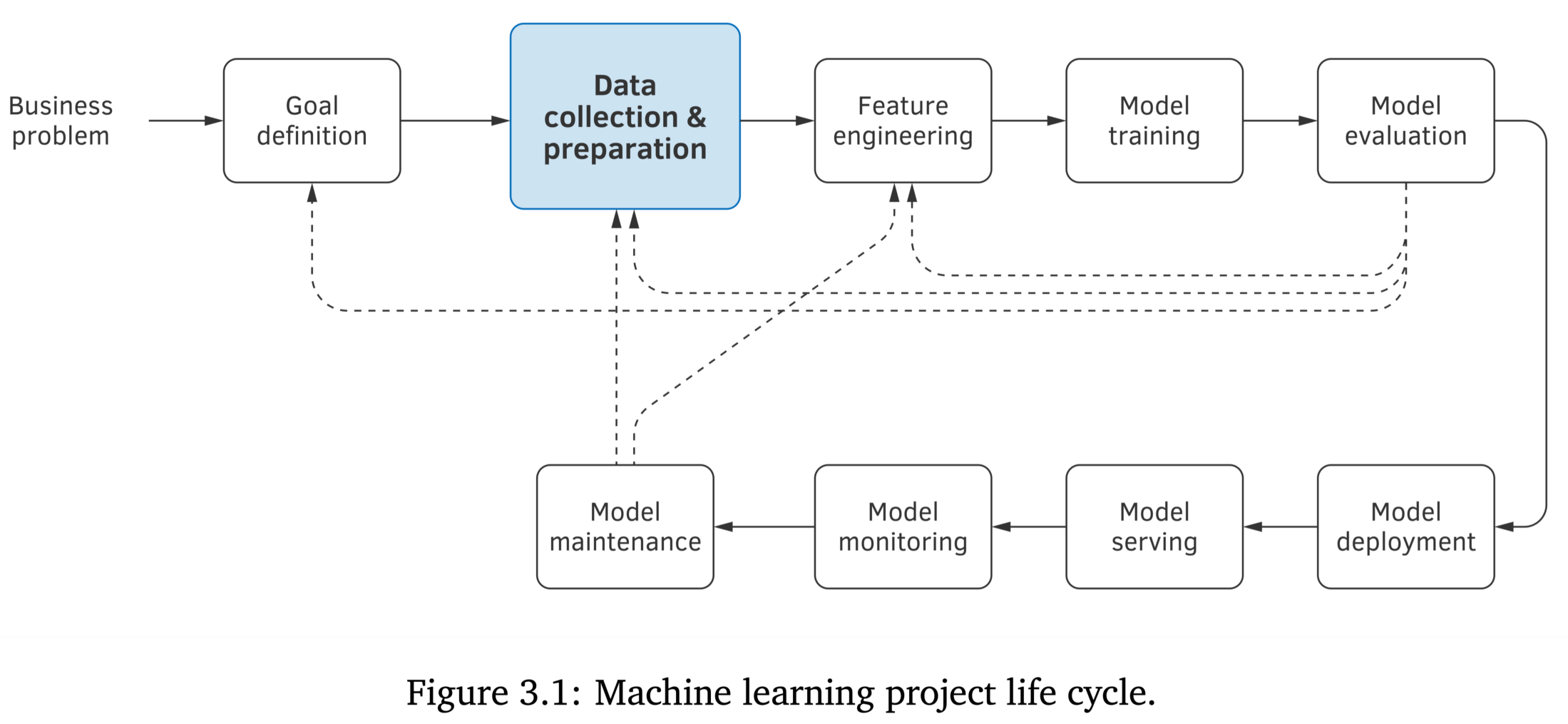
Ingénierie de l’apprentissage automatique

PolynomialFeatures

from sklearn.preprocessing import PolynomialFeatures

poly_features = PolynomialFeatures(degree=2, include_bias=False)
X_poly = poly_features.fit_transform(X)
X[0]
array([-0.75275929])
X_poly[0]
array([-0.75275929,  0.56664654])

sklearn.preprocessing.PolynomialFeatures

Générez une nouvelle matrice d’attributs constituée de toutes les combinaisons polynomiales des attributs avec un degré inférieur ou égal au degré spécifié. Par exemple, si un échantillon d’entrée est bidimensionnel et de la forme \([a, b]\), les attributs polynomials de degré 2 sont \([1, a, b, a^2, ab, b^2]\).

PolynomialFeatures

Étant donné deux attributs \(a\) et \(b\), PolynomialFeatures avec degree=3 ajouterait \(a^2\), \(a^3\), \(b^2\), \(b^3\), ainsi que \(ab\), \(a^2b\), \(ab^2\) !

Avertissement

PolynomialFeatures(degree=d) ajoute \(\frac{(D+d)!}{d!D!}\) attributs, où \(D\) est le nombre initial d’attributs.

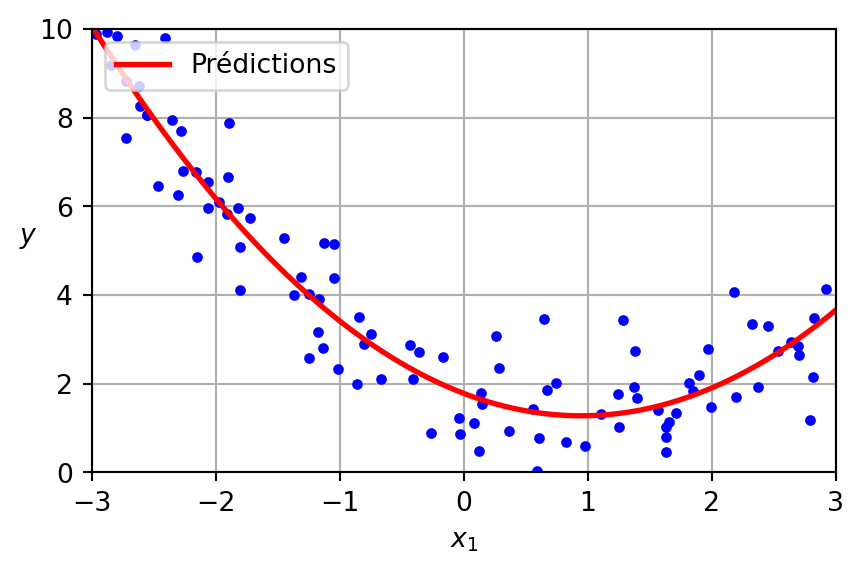
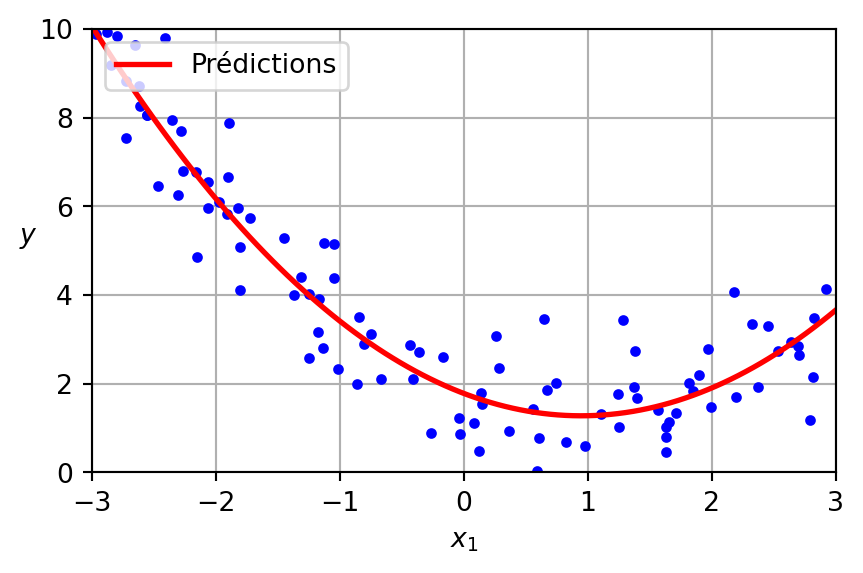
Régression polynomiale

Code 
lin_reg = LinearRegression()
lin_reg = lin_reg.fit(X_poly, y)

X_new = np.linspace(-3, 3, 100).reshape(100, 1)
X_new_poly = poly_features.transform(X_new)
y_new = lin_reg.predict(X_new_poly)

plt.figure(figsize=(5, 3))
plt.plot(X, y, "b.")
plt.plot(X_new, y_new, "r-", linewidth=2, label="Prédictions")
plt.xlabel("$x_1$")
plt.ylabel("$y$", rotation=0)
plt.legend(loc="upper left")
plt.axis([-3, 3, 0, 10])
plt.grid()
plt.show()

LinearRegression sur PolynomialFeatures

lin_reg = LinearRegression()
lin_reg.fit(X_poly, y)

Régression polynomiale

Les données ont été générées selon l’équation suivante, avec l’inclusion de bruit gaussien.

\[ y = 0.5 x^2 - 1.0 x + 2.0 \]

Présenté ci-dessous est le modèle appris.

\[ \hat{y} = 0.56 x^2 + (-1.06) x + 1.78 \]

lin_reg.coef_, lin_reg.intercept_
(array([[-1.06633107,  0.56456263]]), array([1.78134581]))

Les données

La taille compte

“Cependant, ces résultats suggèrent que nous devrions peut-être reconsidérer l’équilibre entre passer du temps et de l’argent à développer des algorithmes, contre investir dans le développement de corpus.”

Efficacité déraisonnable des données

Définition

L’augmentation des données (data augmentation) est une technique utilisée pour accroître la diversité d’un ensemble de données en appliquant diverses transformations aux données existantes.

Augmentation des données

Prologue

Lectures complémentaires

Résumé

  • Encodage des attributs : Évaluation des techniques éviter des biais et possiblement faciliter l’apprentissage.
  • Prétraitement :
    • Mise à l’échelle des données
    • Gestion des valeurs manquantes
    • Gestion du déséquilibre des classes
  • Taille de l’ensemble d’entraînement : Impact sur l’efficacité du modèle et la généralisation.

Prochain cours

  • Introduction aux réseaux neuronaux artificiels.

Références

Banko, Michele, et Eric Brill. 2001. « Scaling to very very large corpora for natural language disambiguation ». In Proceedings of the 39th Annual Meeting on Association for Computational Linguistics, 26‑33. ACL ’01. USA: Association for Computational Linguistics. https://doi.org/10.3115/1073012.1073017.
Burkov, A. 2020. Machine Learning Engineering. True Positive Incorporated. https://books.google.ca/books?id=HeXizQEACAAJ.
Burkov, Andriy. 2019. The Hundred-Page Machine Learning Book. Andriy Burkov.
Chawla, N V, K W Bowyer, L O Hall, et W P Kegelmeyer. 2002. « SMOTE: Synthetic minority over-sampling technique ». Journal of Artificial Intelligence Research 16: 321‑57.
Géron, Aurélien. 2022. Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow. 3ᵉ éd. O’Reilly Media, Inc.
Halevy, Alon, Peter Norvig, et Fernando Pereira. 2009. « The Unreasonable Effectiveness of Data ». IEEE Intelligent Systems 24 (2): 8‑12.
Kaplan, Jared, Sam McCandlish, Tom Henighan, Tom B. Brown, Benjamin Chess, Rewon Child, Scott Gray, Alec Radford, Jeffrey Wu, et Dario Amodei. 2020. « Scaling Laws for Neural Language Models ». https://arxiv.org/abs/2001.08361.
Pradipta, Gede Angga, Retantyo Wardoyo, Aina Musdholifah, I Nyoman Hariyasa Sanjaya, et Muhammad Ismail. 2021. « SMOTE for Handling Imbalanced Data Problem : A Review ». 2021 Sixth International Conference on Informatics and Computing (ICIC) 00: 1‑8. https://doi.org/10.1109/icic54025.2021.9632912.
Russell, Stuart, et Peter Norvig. 2020. Artificial Intelligence: A Modern Approach. 4ᵉ éd. Pearson. http://aima.cs.berkeley.edu/.
Sakai, Masato, Akihisa Sakurai, Siyuan Lu, Jorge Olano, Conrad M. Albrecht, Hendrik F. Hamann, et Marcus Freitag. 2024. « AI-accelerated Nazca survey nearly doubles the number of known figurative geoglyphs and sheds light on their purpose ». Proceedings of the National Academy of Sciences 121 (40): e2407652121. https://doi.org/10.1073/pnas.2407652121.
Shumailov, Ilia, Zakhar Shumaylov, Yiren Zhao, Nicolas Papernot, Ross Anderson, et Yarin Gal. 2024. « AI models collapse when trained on recursively generated data ». Nature 631 (8022): 755‑59. https://doi.org/10.1038/s41586-024-07566-y.

Annexe : Pipeline

Pipeline

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler

num_pipeline = Pipeline([
        ('imputer', SimpleImputer(strategy="median")),
        ('attribs_adder', CombinedAttributesAdder()),
        ('std_scaler', StandardScaler()),
        ])

training_num_tr = num_pipeline.fit_transform(training_num)

full_pipeline = ColumnTransformer([
        ("num", num_pipeline, num_attribs),
        ("cat", OneHotEncoder(), ["sequence"]),
    ])

training_prepared = full_pipeline.fit_transform(training)

Marcel Turcotte

Marcel.Turcotte@uOttawa.ca

École de science informatique et de génie électrique (SIGE)

Université d’Ottawa

GPT-4o interactions 2024-09-30

J’ai présenté à GPT-4o une image du personnage principal de Marcel the Shell With Shoes On et j’ai eu les interactions suivantes.

Marcel: How would you describe the subject of the image, its artistic quality, technique, and rendering style?

GPT-4o: The image depicts a whimsical character that resembles a small shell with one large, expressive eye. It stands on two legs wearing shoes, giving it a cute and almost anthropomorphic appearance. The character has a surreal and quirky look, which lends it a sense of personality and charm.

Artistic Quality:

The image is rendered with a high degree of polish and smoothness, possibly created digitally. The textures, shading, and lighting are soft and subtle, giving the character a smooth and rounded look. The rendering captures a delicate balance between realism (in the textures of the shell and shoes) and cartoon-like abstraction (in the exaggerated eye and small stature).

Technique:

The artist appears to have employed a blend of digital painting and 3D-like modeling techniques, with careful attention to detail in the reflections in the eye and the textures of the shell and shoes. The color palette is muted, using soft tones that evoke a gentle, friendly atmosphere.

Rendering Style:

The rendering style is a mix of minimalist and hyperrealist elements. The minimalism is seen in the simplified forms of the character—particularly the body and legs—while the hyperrealism comes through in the detailing of the eye and the subtle textures. This gives the character a tactile, almost tangible quality while maintaining its fantastical, imaginative essence.

The overall effect of the design is both charming and surreal, combining everyday objects (a shell, shoes) with anthropomorphic and fantastical elements to create a unique, playful character.

Marcel: Create an image based on the following description: The image depicts a whimsical character that resembles a small shell with one large, expressive eye. It stands on two legs wearing shoes, giving it a cute and almost anthropomorphic appearance. The character has a surreal and quirky look, which lends it a sense of personality and charm.

Artistic Quality:

The image is rendered with a high degree of polish and smoothness, possibly created digitally. The textures, shading, and lighting are soft and subtle, giving the character a smooth and rounded look. The rendering captures a delicate balance between realism (in the textures of the shell and shoes) and cartoon-like abstraction (in the exaggerated eye and small stature).

Technique:

The artist appears to have employed a blend of digital painting and 3D-like modeling techniques, with careful attention to detail in the reflections in the eye and the textures of the shell and shoes. The color palette is muted, using soft tones that evoke a gentle, friendly atmosphere.

Rendering Style:

The rendering style is a mix of minimalist and hyperrealist elements. The minimalism is seen in the simplified forms of the character—particularly the body and legs—while the hyperrealism comes through in the detailing of the eye and the subtle textures. This gives the character a tactile, almost tangible quality while maintaining its fantastical, imaginative essence.

The overall effect of the design is both charming and surreal, combining everyday objects (a shell, shoes) with anthropomorphic and fantastical elements to create a unique, playful character.

GTP-4o: Here is the image based on the description you provided. Let me know if you’d like to make any adjustments!