Entraîner un réseau de neurones artificiels (partie 2)
CSI 4106 - Automne 2025
Version: oct. 26, 2025 12h06
Préambule
Message du Jour
Résultats d’apprentissage
- Algorithme de Rétropropagation :
- Discuter des passes avant et arrière, en soulignant le calcul des gradients à l’aide de dérivées partielles pour mettre à jour les poids.
- Problème de Gradient Évanescent :
- Exposer le problème et présenter des stratégies d’atténuation, telles que l’utilisation de fonctions d’activation comme ReLU ou l’initialisation des poids avec une attention particulière.
Rétropropagation
Rétropropagation
Apprentissage de représentations par rétropropagation des erreurs
David E. Rumelhart, Geoffrey E. Hinton & Ronald J. Williams
Nous décrivons une nouvelle procédure d’apprentissage, la rétropropagation, pour les réseaux d’unités semblables à des neurones. La procédure ajuste à plusieurs reprises les poids des connexions dans le réseau afin de minimiser une mesure de la différence entre le vecteur de sortie réel du réseau et le vecteur de sortie souhaité. En conséquence des ajustements de poids, les unités internes ‘cachées’ qui ne font pas partie de l’entrée ou de la sortie en viennent à représenter des attributs importants du domaine de la tâche, et les régularités de la tâche sont capturées par les interactions de ces unités. La capacité à créer de nouveaux attributs utiles distingue la rétropropagation des méthodes antérieures, plus simples, telles que la procédure de convergence du perceptron.
Avant la rétropropagation
Des limitations, telles que l’incapacité à résoudre la tâche de classification XOR, ont essentiellement stoppé la recherche sur les réseaux neuronaux.
Le perceptron était limité à une seule couche, et il n’existait aucune méthode connue pour entraîner un perceptron multi-couches.
Les perceptrons à une seule couche sont limités à résoudre des tâches de classification qui sont linéairement séparables.
Rétropropagation : contributions
Le modèle utilise l’erreur quadratique moyenne comme fonction de perte.
La descente de gradient est utilisée pour minimiser la perte.
Une fonction d’activation sigmoïde est utilisée au lieu d’une fonction de seuil, car sa dérivée fournit des informations précieuses pour la descente de gradient.
Montre comment mettre à jour les poids internes en utilisant un algorithme en deux passes consistant en une passe avant et une passe arrière.
Permet l’entraînement des perceptrons multi-couches.
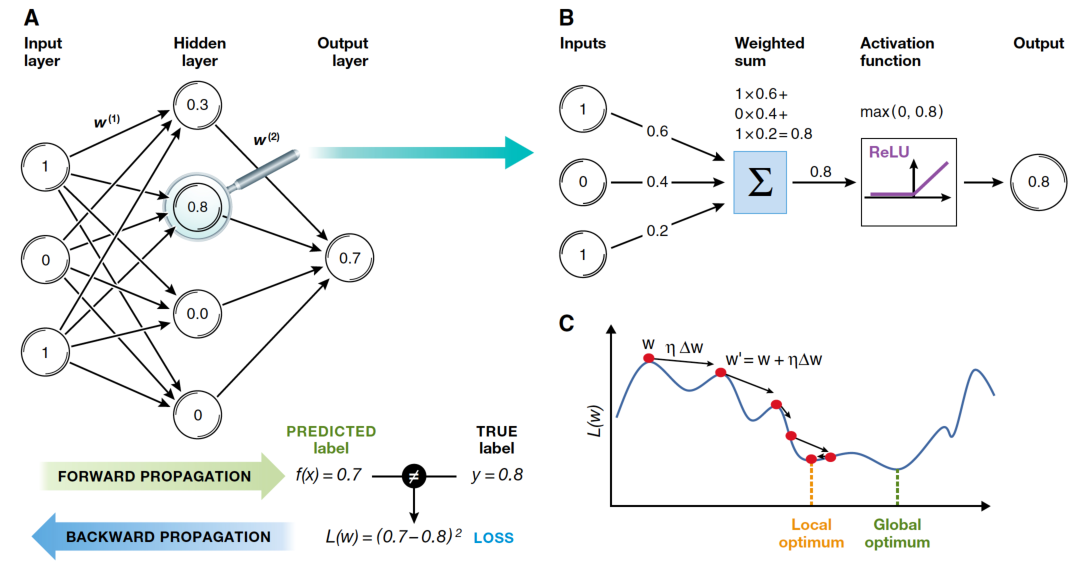
Idée Conceptuelle
Idée Conceptuelle (suite)
Idée Conceptuelle (suite)
Rétropropagation
Rétropropagation (backprop) est un algorithme pour calculer méthodiquement les dérivées partielles de la fonction de perte d’un réseau de neurones par rapport à chaque paramètre de poids et de biais.
Rétropropagation applique la règle de la chaîne (chain rule) du calcul différentiel récursivement pour calculer \(\frac{\partial J}{\partial w_{i,j}^{(\ell)}}\) pour tous les paramètres du réseau \(w_{i,j}^{(\ell)}\) de manière efficace, en utilisant des quantités intermédiaires du passage avant, où \(w_{i,j}^{(\ell)}\) désigne le paramètre \(w_{i,j}\) de la couche \(\ell\).
Règle de la chaîne
Étant donné,
\[ h(x) = f(g(x)) \]
en utilisant la notation de Lagrange, nous avons
\[ h^\prime(x) = f^\prime(g(x)) g^\prime(x) \]
ou de manière équivalente en utilisant la notation de Leibniz
\[ \frac{dz}{dx} = \frac{dz}{dy} \cdot \frac{dy}{dx} \]
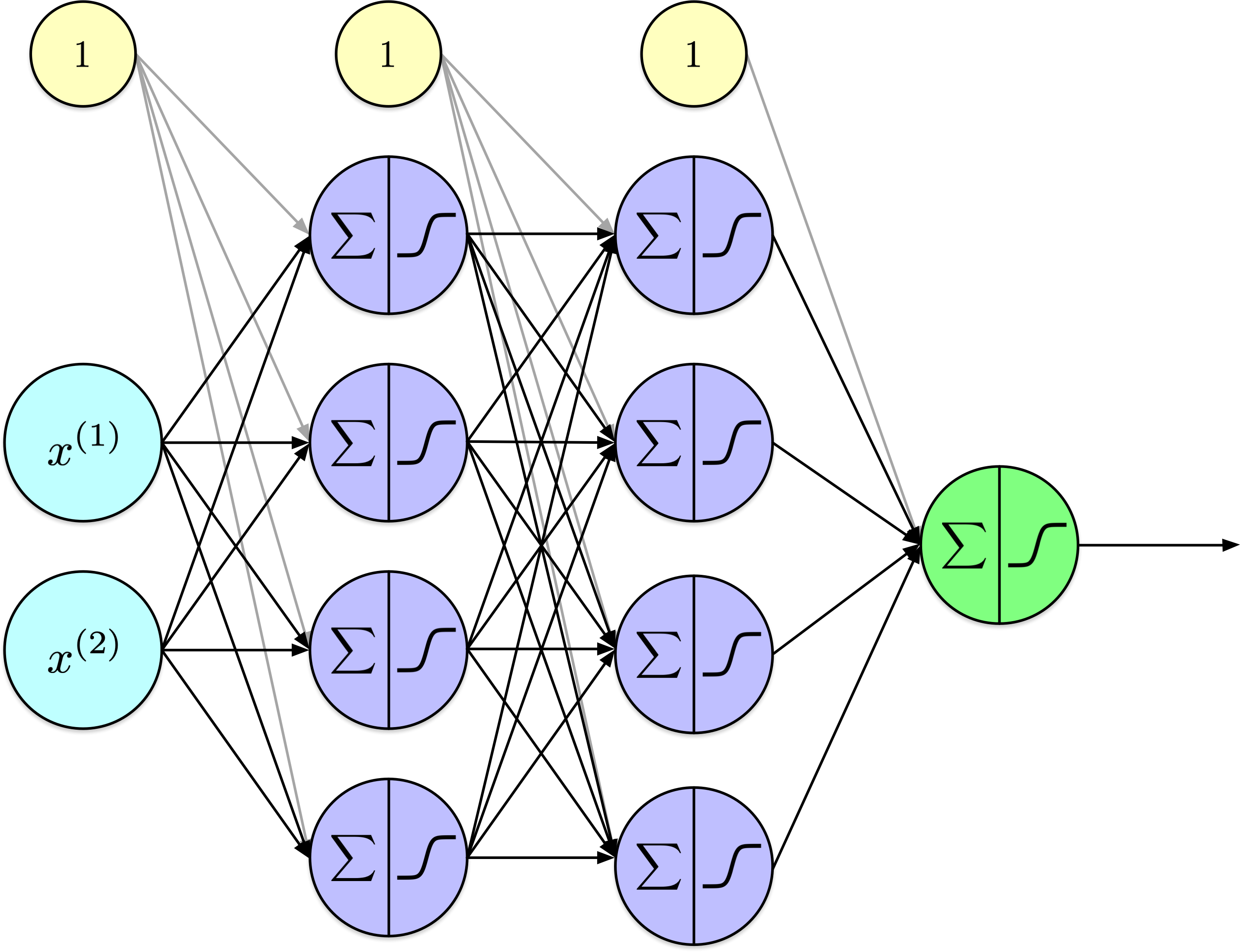
Application récursive
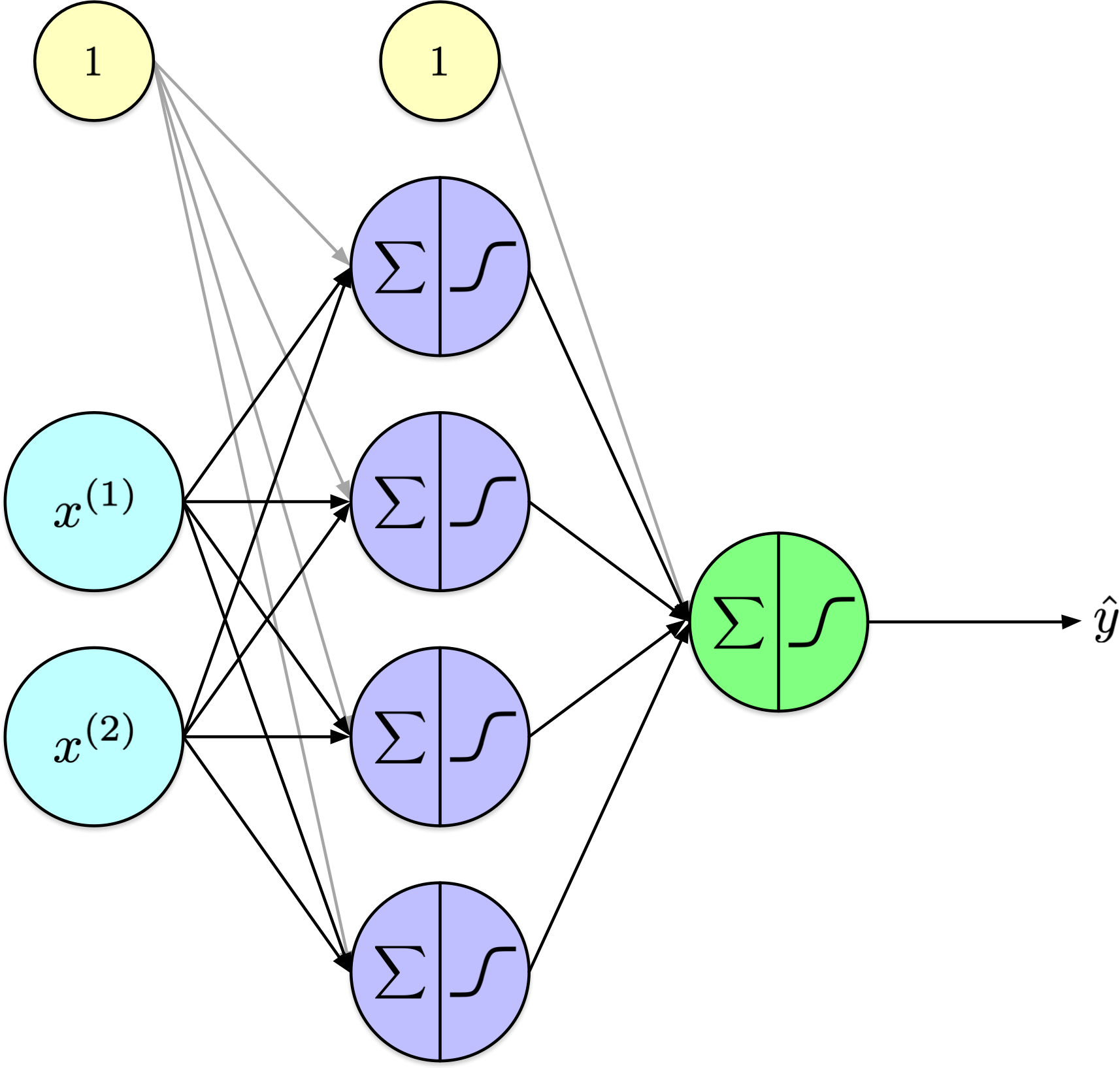
Graphe computationnel
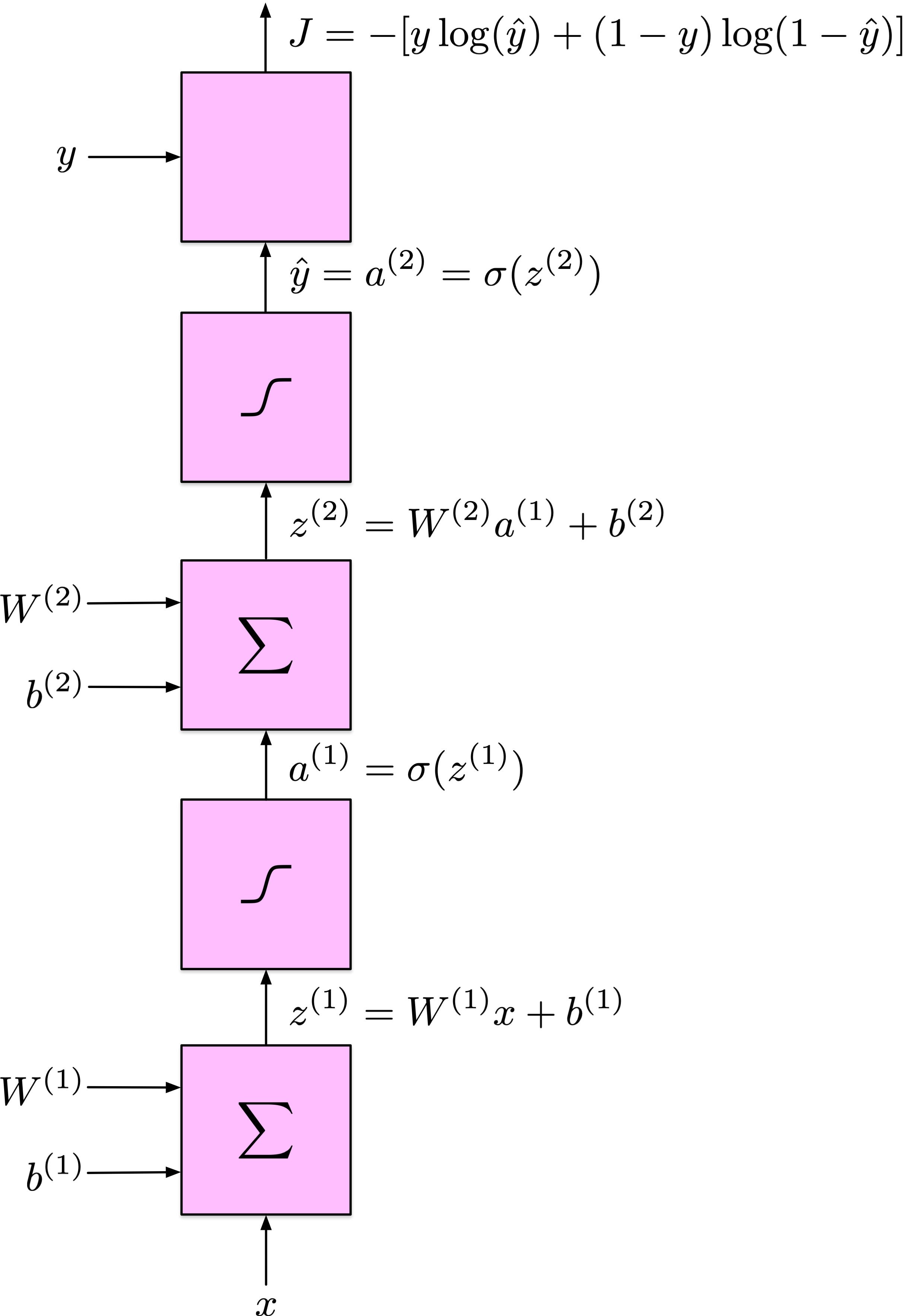
Entrée scalaire; un nœud caché
Dérivées
\[ \frac{\partial J}{\partial \hat{y}} \]
\[ \frac{\partial \hat{y}}{\partial z_2} \]
\[ \frac{\partial z_2}{\partial w_2}, \quad \frac{\partial z_2}{\partial b_2}, \quad \frac{\partial z_2}{\partial a_1}, \]
\[ \frac{\partial a_1}{\partial z_1}, \]
\[ \frac{\partial z_1}{\partial w_1}, \quad \frac{\partial z_1}{\partial b_1}, \quad \frac{\partial z_1}{\partial x}, \]
Dérivées
Dérivées
Dérivées
Dérivées
Dérivées
Dérivées combinées
Pour \(w_2\) :
\[ \frac{\partial J}{\partial w_2}=\frac{\partial J}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial z_2} \cdot \frac{\partial z_2}{\partial w_2}=\left[-\left(\frac{y}{\hat{y}}-\frac{1-y}{1-\hat{y}}\right)\right] \cdot(\hat{y}(1-\hat{y})) \cdot a_1 \]
Se simplifie en :
\[ \frac{\partial J}{\partial w_2}=(\hat{y}-y) a_1 \]
Dérivées combinées
Dérivées combinées
Pour \(w_1\) :
\[ \frac{\partial J}{\partial w_1}=\frac{\partial J}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial z_2} \cdot \frac{\partial z_2}{\partial a_1} \cdot \frac{\partial a_1}{\partial z_1} \cdot \frac{\partial z_1}{\partial w_1} \]
Substituer :
\[ =\left[-\left(\frac{y}{\hat{y}}-\frac{1-y}{1-\hat{y}}\right)\right] \cdot(\hat{y}(1-\hat{y})) \cdot w_2 \cdot\left(a_1\left(1-a_1\right)\right) \cdot x \]
Se simplifie à :
\[ \frac{\partial J}{\partial w_1}=(\hat{y}-y) w_2\left(a_1\left(1-a_1\right)\right) x \]
Dérivées combinées
Pour \(b_1\) :
\[ \frac{\partial J}{\partial b_1}=\frac{\partial J}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial z_2} \cdot \frac{\partial z_2}{\partial a_1} \cdot \frac{\partial a_1}{\partial z_1} \cdot \frac{\partial z_1}{\partial b_1} \]
Substituer :
\[ =(\hat{y}-y) w_2\left(a_1\left(1-a_1\right)\right) \cdot 1 \]
Se simplifie à :
\[ \frac{\partial J}{\partial b_1}=(\hat{y}-y) w_2\left(a_1\left(1-a_1\right)\right) \]
Dérivées clés
\[ \begin{align} \frac{\partial J}{\partial w_2} & = (\hat{y}-y) a_1 \\ \frac{\partial J}{\partial b_2} & = \hat{y}-y \\ \frac{\partial J}{\partial w_1} & = (\hat{y}-y) w_2\left(a_1\left(1-a_1\right)\right) x \\ \frac{\partial J}{\partial b_1} & = (\hat{y}-y) w_2\left(a_1\left(1-a_1\right)\right) \\ \end{align} \]
Exploration
Forward
Rétropropagation
def backward():
global alpha, w1, b1, w2, b2, a1, z1, z2, y, y_hat
grad_J_w2 = (y_hat - y) * a1
grad_J_b2 = y_hat - y
grad_J_w1 = (y_hat - y) * w2 * (a1 * (1-a1)) * x
grad_J_b1 = (y_hat - y) * w2 * (a1 * (1-a1))
w2 = w2 - alpha * grad_J_w2
b2 = b2 - alpha * grad_J_b2
w1 = w1 - alpha * grad_J_w1
b1 = b1 - alpha * grad_J_b1Entraînement
Dérivées clés
\[ \begin{align} \frac{\partial J}{\partial w_2} & = \frac{\partial J}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial z_2} \cdot \frac{\partial z_2}{\partial w_2}\\ \frac{\partial J}{\partial b_2} & = \frac{\partial J}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial z_2} \cdot \frac{\partial z_2}{\partial b_2}\\ \frac{\partial J}{\partial w_1} & = \frac{\partial J}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial z_2} \cdot \frac{\partial z_2}{\partial a_1} \cdot \frac{\partial a_1}{\partial z_1} \cdot \frac{\partial z_1}{\partial w_1}\\ \frac{\partial J}{\partial b_1} & = \frac{\partial J}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial z_2} \cdot \frac{\partial z_2}{\partial a_1} \cdot \frac{\partial a_1}{\partial z_1} \cdot \frac{\partial z_1}{\partial b_1}\\ \end{align} \]
Dérivées clés
Soit \[ \begin{align} \delta_1 & = \frac{\partial J}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial z_2} \\ \delta_2 & = \delta_1 \cdot \frac{\partial z_2}{\partial a_1} \cdot \frac{\partial a_1}{\partial z_1} \end{align} \]
Réécrire \[ \begin{align} \frac{\partial J}{\partial w_2} & = \delta_1 \cdot \frac{\partial z_2}{\partial w_2}\\ \frac{\partial J}{\partial b_2} & = \delta_1 \cdot \frac{\partial z_2}{\partial b_2}\\ \frac{\partial J}{\partial w_1} & = \delta_2 \cdot \frac{\partial z_1}{\partial w_1}\\ \frac{\partial J}{\partial b_1} & = \delta_2 \cdot \frac{\partial z_1}{\partial b_1}\\ \end{align} \]
Rétropropagation : à haut niveau
(Création du Graphe computationnel)
Initialisation
Passage avant
Calcul de la perte
Passage arrière (Rétropropagation)
Mettre à jour les paramètres et répéter de 3 à 6.
Rétropropagation : détaillé
(Créer le graphe computationnel.)
Initialiser les poids et biais.
Passage avant : en partant de l’entrée, calculer la sortie de chaque opération dans le graphe et stocker ces valeurs.
Calculer la perte.
Passage arrière : en partant de la sortie et en revenant en arrière, pour chaque opération.
Calculer la dérivée de la sortie par rapport à chacune des entrées.
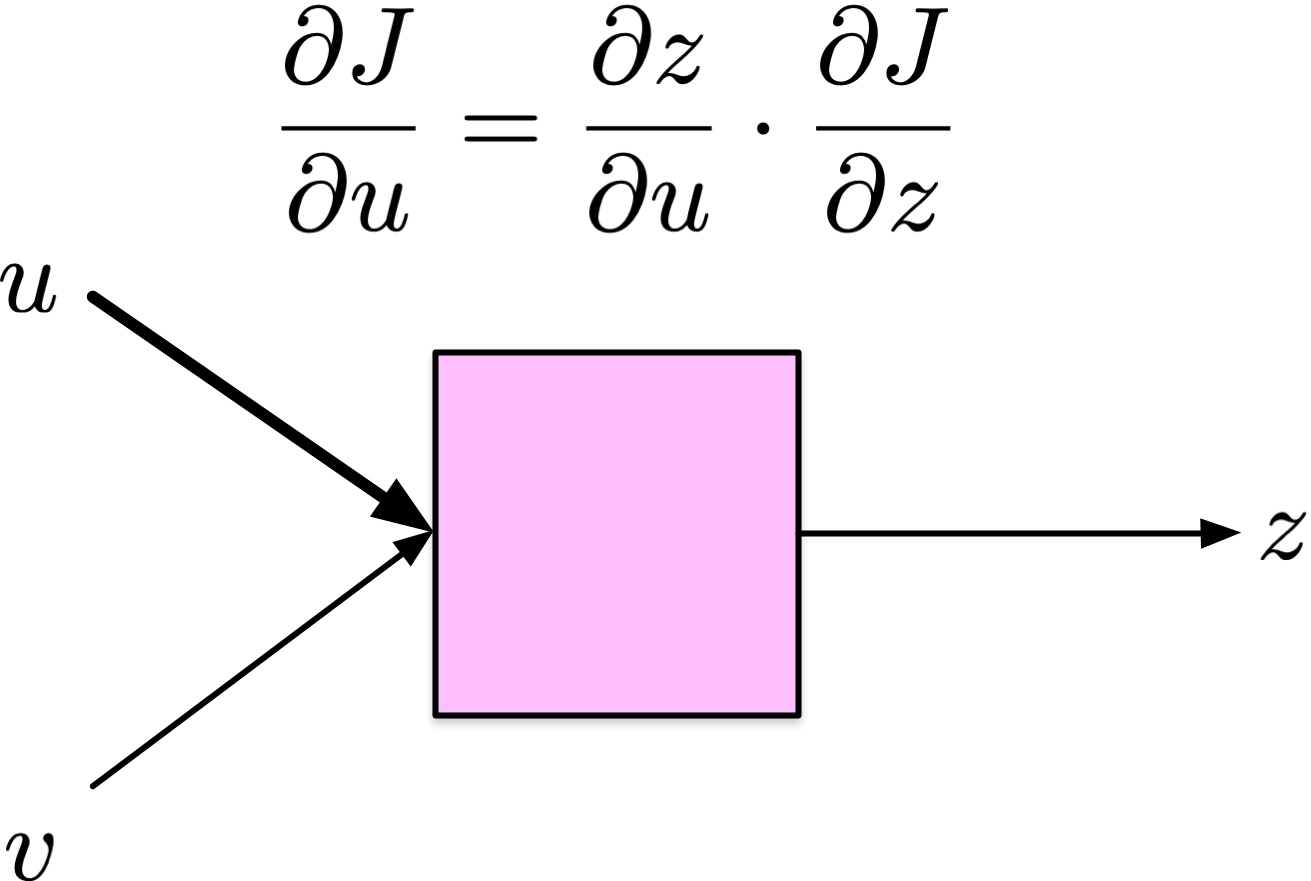
Pour chaque entrée \(u\),
\[ \delta_u = \frac{\partial J}{\partial u} = \frac{\partial z}{\partial u} \cdot \frac{\partial J}{\partial z} \]
- Mettre à jour les paramètres et répéter de 3 à 6.
Rétropropagation : 2. Initialisation
Initialiser les poids et biais du réseau de neurones.
Initialisation à zéro- Tous les poids sont initialisés à zéro.
- Problèmes de symétrie, tous les neurones produisent des sorties identiques, empêchant un apprentissage efficace.
- Initialisation aléatoire
- Les poids sont initialisés aléatoirement, souvent en utilisant une distribution uniforme ou normale.
- Brise la symétrie entre les neurones, leur permettant d’apprendre.
- Si mal échelonné, conduit à une convergence lente ou à des gradients qui disparaissent/explosent.
Rétropropagation : 3. Propagation Avant
Pour chaque exemple dans le jeu d’entraînement (ou dans un mini-lot) :
Couche d’Entrée : Transmettre les attributs d’entrée à la première couche.
Couches Cachées : Pour chaque couche cachée, calculer les activations (sortie) en appliquant la somme pondérée des entrées plus le biais, suivie d’une fonction d’activation (par exemple, sigmoïde, ReLU).
Couche de Sortie : Même processus que pour les couches cachées. Les activations de la couche de sortie représentent les valeurs prédites.
Rétropropagation : 4. Calculer la Perte
Calculez la perte (erreur) en utilisant une fonction de perte appropriée en comparant les valeurs prédites aux valeurs cibles réelles.
Rétropropagation : 5. Passage en arrière
Couche de sortie : Calculer le gradient de la perte par rapport aux poids et biais de la couche de sortie en utilisant la règle de chaîne du calcul différentiel.
Couches cachées : Propager l’erreur en arrière à travers le réseau, couche par couche. Pour chaque couche, calculer le gradient de la perte par rapport aux poids et biais. Utiliser la dérivée de la fonction d’activation pour aider à calculer ces gradients.
Mettre à jour les poids et biais : Ajuster les poids et biais en utilisant les gradients calculés et un taux d’apprentissage, qui détermine la taille de chaque mise à jour.
Rétropropagation - Objectif
- Algorithme pour entraîner les perceptrons multicouches (MLPs) en minimisant une fonction de perte.
- Permet aux couches cachées d’apprendre des représentations internes utiles en ajustant les poids et biais.
Rétropropagation - Idée Principale
Ajuster itérativement les paramètres pour réduire la différence entre les sorties prédites et réelles.
Utilise la descente de gradient sur la fonction de perte :
\[ \theta \leftarrow \theta - \alpha \nabla_\theta J(\theta) \]
où \(\alpha\) est le taux d’apprentissage.
Rétropropagation - Résumé
Créer le graphe computationnel
Initialiser les poids et biais
Passage avant : calculer les activations et la perte.
Passage arrière : calculer les gradients en utilisant la règle de la chaîne.
Mettre à jour les paramètres :
\(W^{(\ell)} \leftarrow W^{(\ell)} - \alpha \frac{\partial J}{\partial W^{(\ell)}}\)
\(b^{(\ell)} \leftarrow b^{(\ell)} - \alpha \frac{\partial J}{\partial b^{(\ell)}}\)
Répéter jusqu’à convergence.
Implémentation
Rétropropagation - Passage Avant
Calculer les activations couche par couche :
\(z^{(\ell)} = W^{(\ell)} a^{(\ell-1)} + b^{(\ell)}\),
\(a^{(\ell)} = \phi(z^{(\ell)})\).
Obtenir la prédiction \(\hat{y}\) et calculer la perte \(J(\hat{y}, y)\).
Rétropropagation - Passage Arrière
- Appliquer la règle de la chaîne pour calculer les dérivées partielles de la perte par rapport à chaque paramètre de manière efficace.
- Propager les gradients des couches de sortie vers les couches d’entrée :
\[ \delta^{(\ell)} = (W^{(\ell+1)} \delta^{(\ell+1)}) \odot \phi'(z^{(\ell)}) \]
SimpleMLP
L’implémentation complète est présentée ci-dessous et sera examinée dans les diapositives suivantes.
Afficher le code
import numpy as np
# Activations & perte
def sigmoid(z):
return 1.0 / (1.0 + np.exp(-z))
def sigmoid_prime(z):
s = sigmoid(z)
return s * (1.0 - s)
def relu(z):
return np.maximum(0.0, z)
def relu_prime(z):
return (z > 0).astype(z.dtype)
def bce_loss(y_true, y_prob, eps=1e-9):
"""Entropie croisée binaire moyennée sur les échantillons (avec découpage pour la stabilité)."""
y_prob = np.clip(y_prob, eps, 1 - eps)
return -np.mean(y_true * np.log(y_prob) + (1 - y_true) * np.log(1 - y_prob))
# Initialisateurs
def he_init(rng, fan_in, fan_out):
# He normal : bon pour ReLU
std = np.sqrt(2.0 / fan_in)
return rng.normal(0.0, std, size=(fan_in, fan_out))
def xavier_init(rng, fan_in, fan_out):
# Glorot/Xavier normal : bon pour sigmoid/tanh
std = np.sqrt(2.0 / (fan_in + fan_out))
return rng.normal(0.0, std, size=(fan_in, fan_out))
# SimpleMLP (API imite NaiveMLP)
class SimpleMLP:
"""
MLP minimal pour la classification binaire.
- Caché : ReLU (par défaut) avec He init ; ou 'sigmoid' avec Xavier init
- Sortie : Sigmoid + BCE (δ_L = a_L - y)
- API : forward -> probas (N,), predict_proba, predict, loss, train
"""
def __init__(self, layer_sizes, lr=0.1, seed=None, l2=0.0,
hidden_activation="relu", lr_decay=None):
"""
layer_sizes : par ex., [2, 4, 4, 1]
lr : taux d'apprentissage
l2 : force de régularisation L2 (0 désactive)
hidden_activation : 'relu' (par défaut) ou 'sigmoid'
lr_decay : flottant optionnel dans (0,1) ; multiplie lr par cela à chaque époque (par ex., 0.9)
"""
self.sizes = list(layer_sizes)
self.lr = float(lr)
self.base_lr = float(lr)
self.lr_decay = lr_decay
self.l2 = float(l2)
self.hidden_activation = hidden_activation
rng = np.random.default_rng(seed)
# Initialiser poids/biais par couche
self.W = []
for din, dout in zip(self.sizes[:-1], self.sizes[1:]):
if hidden_activation == "relu":
Wk = he_init(rng, din, dout)
else:
Wk = xavier_init(rng, din, dout)
self.W.append(Wk)
self.b = [np.zeros(dout) for dout in self.sizes[1:]]
# activations (cachée vs sortie)
def _act(self, z, last=False):
if last:
return sigmoid(z) # couche de sortie
return relu(z) if self.hidden_activation == "relu" else sigmoid(z)
def _act_prime(self, z, last=False):
if last:
return sigmoid_prime(z) # rarement nécessaire avec BCE+sigmoid
return relu_prime(z) if self.hidden_activation == "relu" else sigmoid_prime(z)
# forward (public) : retourne probabilités (N,)
def forward(self, X):
a = X
L = len(self.W)
for ell, (W, b) in enumerate(zip(self.W, self.b), start=1):
a = self._act(a @ W + b, last=(ell == L))
return a.ravel()
# Alias pour correspondre à NaiveMLP
def predict_proba(self, X):
return self.forward(X)
def predict(self, X, threshold=0.5):
return (self.predict_proba(X) >= threshold).astype(int)
def loss(self, X, y):
# BCE + L2 optionnel
p = self.predict_proba(X)
base = bce_loss(y, p)
if self.l2 > 0:
reg = 0.5 * self.l2 * sum((W**2).sum() for W in self.W)
# Normaliser reg par le nombre d'échantillons pour être cohérent avec la perte moyenne
base += reg / max(1, X.shape[0])
return base
# interne : forward caches pour rétropropagation
def _forward_full(self, X):
a = X
activations = [a]
zs = []
L = len(self.W)
for ell, (W, b) in enumerate(zip(self.W, self.b), start=1):
z = a @ W + b
a = self._act(z, last=(ell == L))
zs.append(z)
activations.append(a)
return activations, zs
# entraînement : descente de gradient par mini-lots avec rétropropagation
def train(self, X, y, epochs=30, batch_size=None, verbose=True, shuffle=True):
"""
X : (N, d), y : (N,) dans {0,1}
batch_size : None -> lot complet ; sinon int
"""
N = X.shape[0]
idx = np.arange(N)
B = N if batch_size is None else int(batch_size)
for ep in range(1, epochs + 1):
if shuffle:
np.random.shuffle(idx)
if self.lr_decay:
self.lr = self.base_lr * (self.lr_decay ** (ep - 1))
base_loss = self.loss(X, y)
for start in range(0, N, B):
sl = idx[start:start+B]
Xb = X[sl]
yb = y[sl].reshape(-1, 1) # (B,1)
# Forward caches
activations, zs = self._forward_full(Xb)
A_L = activations[-1] # (B,1)
Bsz = Xb.shape[0]
# Rétropropagation
# Couche de sortie : BCE + sigmoid => delta_L = (A_L - y)
delta = (A_L - yb) # (B,1)
grads_W = [None] * len(self.W)
grads_b = [None] * len(self.b)
# Gradients de la dernière couche
grads_W[-1] = activations[-2].T @ delta / Bsz # (n_{L-1}, 1)
grads_b[-1] = delta.mean(axis=0) # (1,)
# Couches cachées : l = L-1 à 1
for l in range(2, len(self.sizes)):
z = zs[-l] # (B, n_l)
sp = self._act_prime(z, last=False) # (B, n_l)
delta = (delta @ self.W[-l+1].T) * sp # (B, n_l)
grads_W[-l] = activations[-l-1].T @ delta / Bsz # (n_{l-1}, n_l)
grads_b[-l] = delta.mean(axis=0) # (n_l,)
# Régularisation L2 (ajouter aux gradients)
if self.l2 > 0:
for k in range(len(self.W)):
grads_W[k] = grads_W[k] + self.l2 * self.W[k]
# Étape de gradient
for k in range(len(self.W)):
self.W[k] -= self.lr * grads_W[k]
self.b[k] -= self.lr * grads_b[k]
new_loss = self.loss(X, y)
if verbose:
print(f"Époque {ep:3d} | perte {base_loss:.5f} → {new_loss:.5f} | Δ={base_loss - new_loss:.5f} | lr={self.lr:.4f}")Fonctions d’activation
Perte
Initialisateurs
def he_init(rng, fan_in, fan_out):
# He normal : bon pour ReLU
std = np.sqrt(2.0 / fan_in)
return rng.normal(0.0, std, size=(fan_in, fan_out))
def xavier_init(rng, fan_in, fan_out):
# Glorot/Xavier normal : bon pour sigmoid/tanh
std = np.sqrt(2.0 / (fan_in + fan_out))
return rng.normal(0.0, std, size=(fan_in, fan_out))Définition de classe + constructeur
class SimpleMLP:
def __init__(self, layer_sizes, lr=0.1, seed=None, l2=0.0,
hidden_activation="relu", lr_decay=None):
self.sizes = list(layer_sizes)
self.lr = float(lr)
self.base_lr = float(lr)
self.lr_decay = lr_decay
self.l2 = float(l2)
self.hidden_activation = hidden_activation
rng = np.random.default_rng(seed)
# Initialiser les poids/biais par couche
self.W = []
for din, dout in zip(self.sizes[:-1], self.sizes[1:]):
if hidden_activation == "relu":
Wk = he_init(rng, din, dout)
else:
Wk = xavier_init(rng, din, dout)
self.W.append(Wk)
self.b = [np.zeros(dout) for dout in self.sizes[1:]]Forward (public)
Forward (privé)
Entraînement
def train(self, X, y, epochs=30, batch_size=None, verbose=True, shuffle=True):
"""
X: (N, d), y: (N,) dans {0,1}
batch_size: None -> plein lot; sinon int
"""
N = X.shape[0]
idx = np.arange(N)
B = N if batch_size is None else int(batch_size)
for ep in range(1, epochs + 1):
if shuffle:
np.random.shuffle(idx)
if self.lr_decay:
self.lr = self.base_lr * (self.lr_decay ** (ep - 1))
base_loss = self.loss(X, y)
for start in range(0, N, B):
sl = idx[start:start+B]
Xb = X[sl]
yb = y[sl].reshape(-1, 1) # (B,1)
# Caches avant
activations, zs = self._forward_full(Xb)
A_L = activations[-1] # (B,1)
Bsz = Xb.shape[0]
# Rétropropagation
# Couche de sortie : BCE + sigmoïde => delta_L = (A_L - y)
delta = (A_L - yb) # (B,1)
grads_W = [None] * len(self.W)
grads_b = [None] * len(self.b)
# Gradients de la dernière couche
grads_W[-1] = activations[-2].T @ delta / Bsz # (n_{L-1}, 1)
grads_b[-1] = delta.mean(axis=0) # (1,)
# Couches cachées : l = L-1 jusqu'à 1
for l in range(2, len(self.sizes)):
z = zs[-l] # (B, n_l)
sp = self._act_prime(z, last=False) # (B, n_l)
delta = (delta @ self.W[-l+1].T) * sp # (B, n_l)
grads_W[-l] = activations[-l-1].T @ delta / Bsz # (n_{l-1}, n_l)
grads_b[-l] = delta.mean(axis=0) # (n_l,)
# Régularisation L2 (ajouter aux gradients)
if self.l2 > 0:
for k in range(len(self.W)):
grads_W[k] = grads_W[k] + self.l2 * self.W[k]
# Étape de gradient
for k in range(len(self.W)):
self.W[k] -= self.lr * grads_W[k]
self.b[k] -= self.lr * grads_b[k]
new_loss = self.loss(X, y)
if verbose:
print(f"Époque {ep:3d} | perte {base_loss:.5f} → {new_loss:.5f} | Δ={base_loss - new_loss:.5f} | lr={self.lr:.4f}")Test
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import make_circles
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
X, y = make_circles(n_samples=200, factor=0.5, noise=0.08, random_state=1)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0, stratify=y)
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
model = SimpleMLP([2, 4, 4, 1], lr=0.3, seed=42, hidden_activation="relu", l2=0.0, lr_decay=0.95)
model.train(X_train, y_train, epochs=150, batch_size=32, verbose=False)
print("Exactitude de l'entraînement :", accuracy_score(y_train, model.predict(X_train)))
print("Exactitude du test :", accuracy_score(y_test, model.predict(X_test)))Exactitude de l'entraînement : 0.95
Exactitude du test : 0.9166666666666666Différentiation automatique
La différentiation automatique (autodiff) applique systématiquement la règle de la chaîne pour calculer des dérivées exactes des fonctions exprimées sous forme de programmes informatiques. Elle propage les dérivées à travers des opérations élémentaires, soit en avant (des entrées vers les sorties) soit en arrière (des sorties vers les entrées), permettant un calcul de gradient efficace et précis essentiel pour les algorithmes d’optimisation et d’apprentissage.
Entraînement
Gradients évanescents
Problème de gradient évanescent: Les gradients deviennent trop petits, entravant la mise à jour des poids.
La recherche sur les réseaux neuronaux a stagné (à nouveau) au début des années 2000.
Sigmoïde et sa dérivée (plage : 0 à 0,25) étaient des facteurs clés.
Initialisation courante: Poids/biais issus de \(\mathcal{N}(0, 1)\) ont contribué au problème.
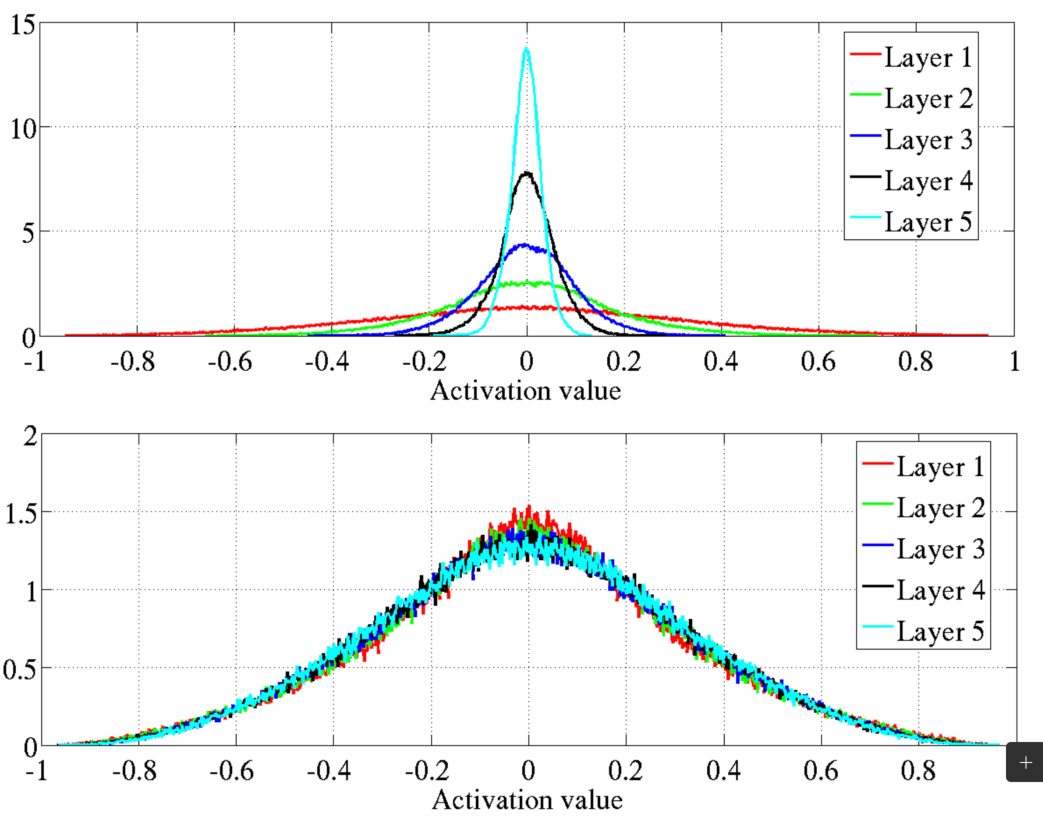
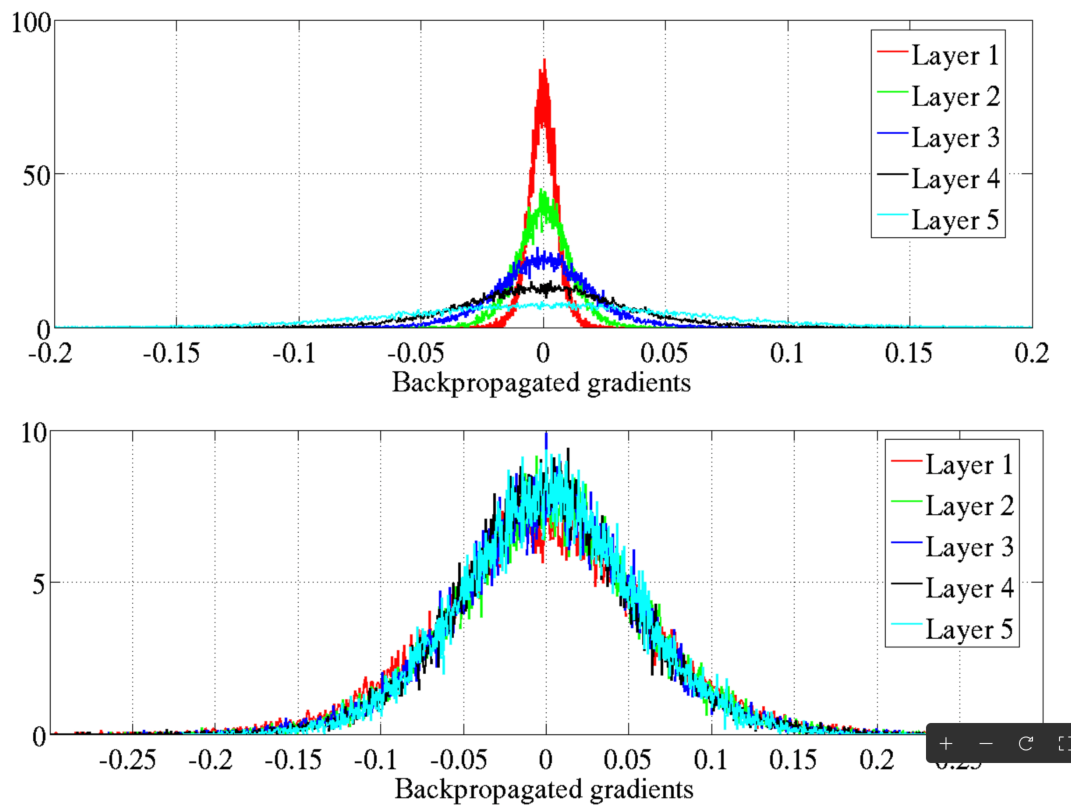
Glorot et Bengio (2010) a mis en lumière les problèmes.
Gradients évanescents : solutions
Fonctions d’activation alternatives : Unité Linéaire Rectifiée (ReLU) et ses variantes (par exemple, Leaky ReLU, Parametric ReLU, et Exponential Linear Unit).
Initialisation des poids : Initialisation Xavier (Glorot) ou He.
Glorot et Bengio
Initialisation He
Une méthode d’initialisation similaire mais légèrement différente conçue pour fonctionner avec ReLU, ainsi que Leaky ReLU, ELU, GELU, Swish, et Mish.
Remarque
L’initialisation aléatoire des poids1 est suffisante pour briser la symétrie dans un réseau de neurones, permettant ainsi que les termes de biais soient fixés à zéro sans nuire à la capacité d’apprentissage du réseau.
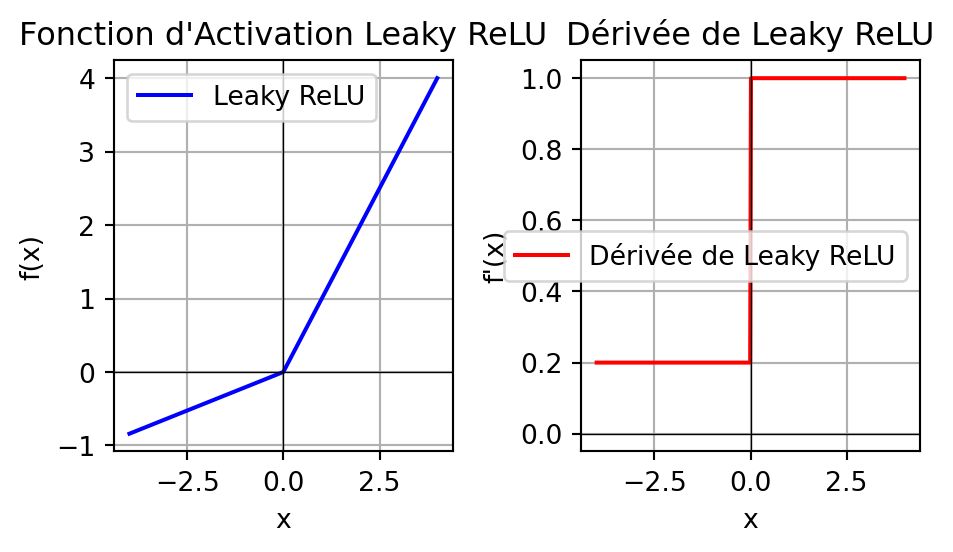
Fonction d’Activation : Leaky ReLU
Afficher le code
import numpy as np
import matplotlib.pyplot as plt
# Définir la fonction Leaky ReLU
def leaky_relu(x, alpha=0.21):
return np.where(x > 0, x, alpha * x)
# Définir la dérivée de la fonction Leaky ReLU
def leaky_relu_derivative(x, alpha=0.2):
return np.where(x > 0, 1, alpha)
# Générer une gamme de valeurs d'entrée
x_values = np.linspace(-4, 4, 400)
# Calculer le Leaky ReLU et sa dérivée
leaky_relu_values = leaky_relu(x_values)
leaky_relu_derivative_values = leaky_relu_derivative(x_values)
# Créer le graphique
plt.figure(figsize=(5, 3))
# Tracer le Leaky ReLU
plt.subplot(1, 2, 1)
plt.plot(x_values, leaky_relu_values, label='Leaky ReLU', color='blue')
plt.title('Fonction d\'Activation Leaky ReLU')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.grid(True)
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.legend()
# Tracer la dérivée du Leaky ReLU
plt.subplot(1, 2, 2)
plt.plot(x_values, leaky_relu_derivative_values, label='Dérivée de Leaky ReLU', color='red')
plt.title('Dérivée de Leaky ReLU')
plt.xlabel('x')
plt.ylabel("f'(x)")
plt.grid(True)
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.legend()
# Afficher les graphiques
plt.tight_layout()
plt.show()Prologue
Résumé
Résumé
| Concept | Rôle |
|---|---|
| Fonctions d’activation | Introduisent la non-linéarité (par exemple, Sigmoïde, ReLU). |
| Fonction de perte | Mesure l’erreur de prédiction (par exemple, Entropie Croisée Binaire). |
| Taux d’apprentissage (α) | Contrôle la taille des pas dans les mises à jour des paramètres. |
| Descente de gradient | Méthode d’optimisation pour l’ajustement des poids. |
| Règle de chaîne | Mécanisme pour propager les dérivées en arrière. |
| Différentiation automatique | Implémentation logicielle de la rétropropagation (par exemple, TensorFlow, PyTorch). |
Résumé
- Réseaux neuronaux artificiels (ANNs) :
- Inspirés des réseaux neuronaux biologiques.
- Composés de neurones interconnectés organisés en couches.
- Applicables à l’apprentissage supervisé, non supervisé, et par renforcement.
- Réseaux neuronaux à propagation directe (FNNs) :
- L’information circule unidirectionnellement de l’entrée à la sortie.
- Composés de couches d’entrée, cachées et de sortie.
- Le nombre de couches et de neurones par couche peut varier.
- Fonctions d’activation :
- Introduisent de la non-linéarité pour permettre l’apprentissage de modèles complexes.
- Fonctions courantes : Sigmoid, Tanh, ReLU, Leaky ReLU.
- Le choix de la fonction d’activation affecte le flux de gradient et les performances du réseau.
- Théorème de l’approximation universelle :
- Un réseau neuronal avec une seule couche cachée peut approximer toute fonction continue.
- Algorithme de rétropropagation :
- L’entraînement implique une passe avant, un calcul de perte, une passe arrière et une mise à jour des poids.
- Utilise la descente de gradient pour minimiser la fonction de perte.
- Permet l’entraînement des perceptrons multicouches en ajustant les poids internes.
- Problème du gradient qui disparaît :
- Les gradients deviennent trop petits lors de la rétropropagation, ce qui freine l’entraînement.
- Stratégies de mitigation : utilisation de fonctions d’activation ReLU et d’une initialisation correcte des poids (Glorot ou He).
- Initialisation des poids :
- L’initialisation aléatoire brise la symétrie et permet un apprentissage efficace.
- L’initialisation Glorot convient aux activations sigmoid et tanh.
- L’initialisation He est optimale pour ReLU et ses variantes.
3Blue1Brown
Une série de vidéos, avec animations, fournissant l’intuition derrière l’algorithme de rétropropagation.
Réseaux neuronaux (playlist)
- Que fait vraiment la rétropropagation ? (12m 47s)
- Calculus de la rétropropagation (10m 18s)
StatQuest
Herman Kamper
Une des séries de vidéos les plus complètes sur l’algorithme de rétropropagation.
Introduction aux réseaux neuronaux (playlist)
- Rétropropagation (sans fourches) (31m 1s)
- Rétropropagation pour un réseau neuronal à propagation avant multicouche (4m 2s)
- Graphes computationnels et différentiation automatique pour les réseaux neuronaux (6m 56s)
- Dérivées communes pour les réseaux neuronaux (7m 18s)
- Une notation générale pour les dérivées (dans les réseaux neuronaux) (7m 56s)
- Fourches dans les réseaux neuronaux (13m 46s)
- Rétropropagation en général (maintenant avec des fourches) (3m 42s)
Livre gratuit avec implémentation
Dans son livre, Neural Networks and Deep Learning, Michael Nielsen fournit une implémentation complète d’un réseau neuronal en Python.
Prochaine leçon
- Nous introduirons différentes architectures de réseaux neuronaux artificiels.
Références
Marcel Turcotte
École de science informatique et de génie électrique (SIGE)
Université d’Ottawa