Softmax, entropie croisée, régularisation

CSI 4506 - Automne 2025

Marcel Turcotte

Version: oct. 28, 2025 15h35

Préambule

Message du jour

Why 2025 is the single most pivotal year in our lifetime, Peter Leyden, Big Think, YouTube, 2025-10-20.

Objectifs d’apprentissage

• Couche Softmax :
  • Décrire sa fonctionnalité dans la conversion des logits en distributions de probabilités pour les tâches de classification.
• Perte d’Entropie Croisée :
  • Expliquer son rôle dans la mesure de la dissimilarité entre les distributions de probabilités prédites et réelles.
• Techniques de Régularisation :
  • Explorer des méthodes comme la régularisation L1, L2 et le dropout pour améliorer les capacités de généralisation des réseaux neuronaux.

Dans le cours précédent, nous avons examiné l’algorithme de rétropropagation, qui offre une méthode systématique pour calculer les dérivées partielles de la fonction de perte. Ce calcul est essentiel pour appliquer l’algorithme de descente de gradient, permettant ainsi l’ajustement des poids dans un réseau de neurones profond. Aujourd’hui, nous aborderons un programme intensif. Nous nous intéressons aux couches de sortie et aux techniques de régularisation.

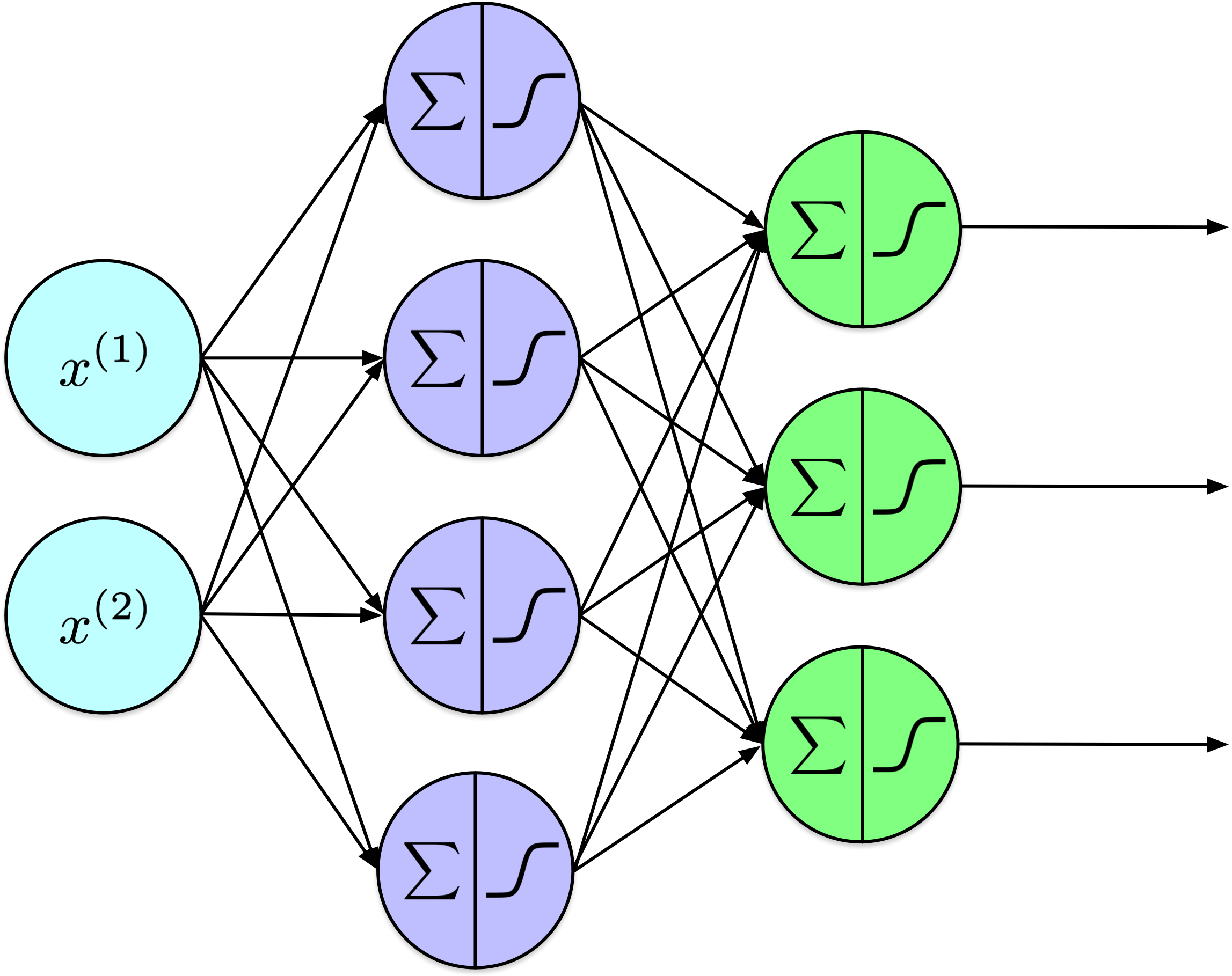
Couche de sortie

Couche de sortie : tâche de régression

• # de neurones de sortie :
  • 1 par dimension
• Fonction d’activation de la couche de sortie :
  • Aucune, ReLU/softplus si positif, sigmoid/tanh si borné
• Fonction de perte :
  • MeanSquaredError

Commen choisit-on les fonctions d’activation?

Dans un réseau feed-forward, les fonctions d’activation dans les couches cachées sont choisies principalement pour leur impact sur la performance et la convergence, tandis que la fonction d’activation dans la couche de sortie est sélectionnée selon les exigences de la tâche.

• Couches cachées :

  La fonction d’activation (par exemple, ReLU, GELU, tanh) affecte principalement la dynamique de l’entraînement; comme le flux de gradient, la force de non-linéarité et le taux de convergence. Le choix est généralement empirique, guidé par la performance, la stabilité numérique et le comportement d’optimisation.

• Couche de sortie :

  La fonction d’activation est déterminée par la nature de la tâche de prédiction :

  • Régression : linéaire, ReLU, ou softplus (selon les contraintes de plage)
  • Classification binaire : sigmoïde
  • Classification multi-classes : softmax
  • Classification multi-étiquettes : sigmoïde (par unité de sortie)

Exemples de problèmes de régression à sorties multiples (2–4 sorties) incluent :

• 2 sorties :

  • Prédire à la fois la latitude et la longitude d’un emplacement à partir d’une image.
  • Estimer la largeur et la hauteur d’une boîte englobante en détection d’objets.
  • Prévoir simultanément la température et l’humidité.

• 3 sorties :

  • Prédire les coordonnées x, y, z d’un point dans l’espace (par exemple, localisation d’une articulation de main).
  • Estimer les valeurs de couleur RGB à partir de mesures spectrales.

• 4 sorties :

  • Prédire les coordonnées de la boîte englobante — \((x_{min}, y_{min}, x_{max}, y_{max})\) — en détection d’objets.

Dans un problème de détection d’objet, la détermination de la boîte englobante est un exemple de tâche de régression où la sortie est multidimensionnelle.

Couche de sortie : Multi-étiquette

Cependant, ce réseau n’est pas adapté à la classification. Voyez-vous pourquoi ?

Avec la fonction d’activation sigmoïde, ce réseau effectue des prédictions multi-étiquettes.

Couche de sortie : tâche de classification

• # de neurones de sortie :
  • 1 si binaire, 1 par classe si multiclasse ou multilabel.
• Fonction d’activation de la couche de sortie :
  • sigmoid si binaire ou multilabel, softmax si multiclasses.
• Fonction de perte :
  • entropie croisée

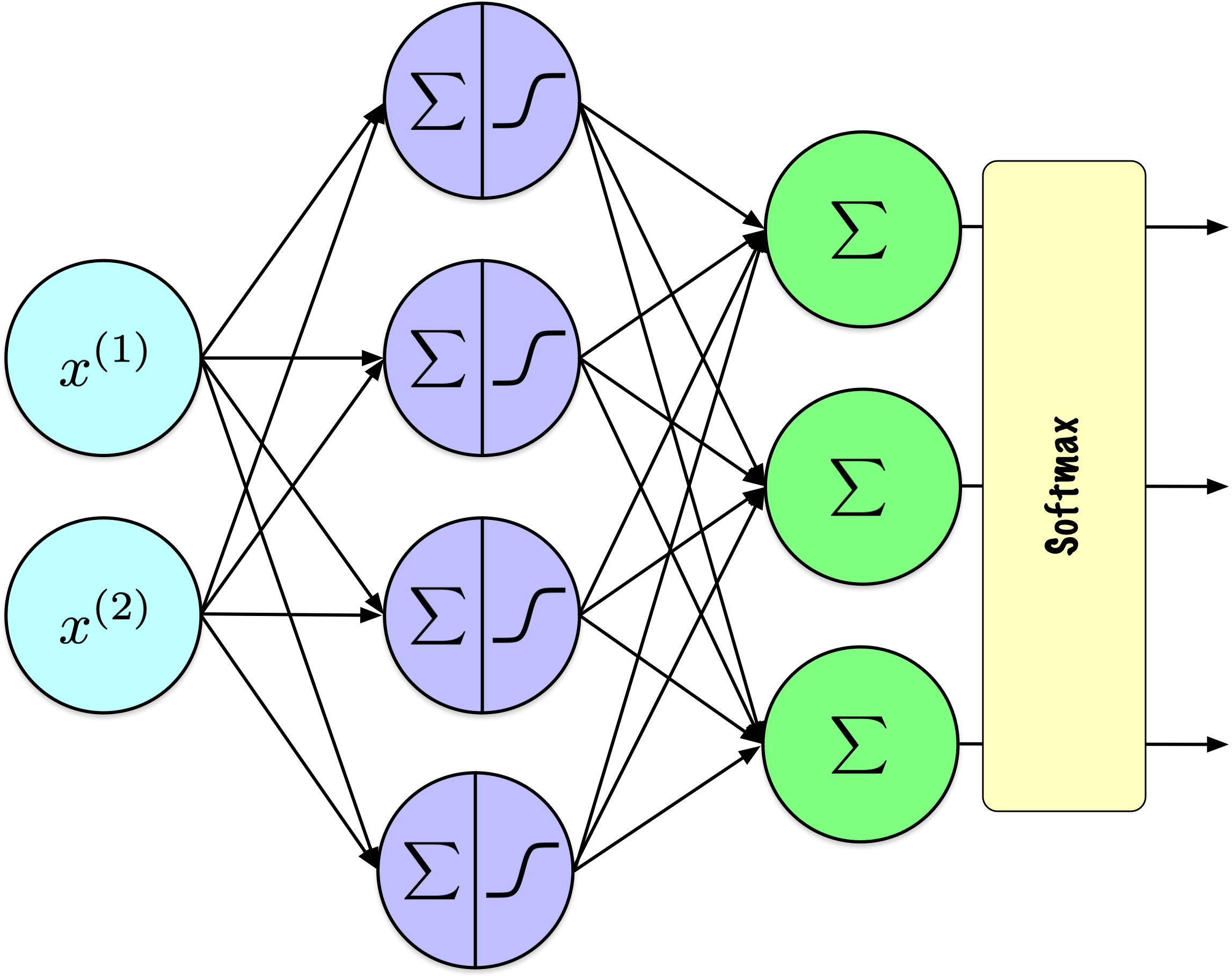
Softmax

Remarquez que j’ai révisé la représentation des nœuds de sortie pour indiquer que la fonction softmax est appliquée à l’ensemble de la couche, plutôt qu’à des nœuds individuels. Cette fonction transforme les valeurs brutes de sortie de la couche en probabilités qui totalisent 1, facilitant ainsi la classification multiclasses. Cette caractéristique la distingue des fonctions d’activation comme ReLU ou sigmoid, qui sont généralement appliquées indépendamment à la sortie de chaque nœud.

La fonction \(\argmax\) n’est pas appropriée pour l’optimisation par des méthodes basées sur les gradients, car sa dérivée est nulle dans tous les cas, comme pour les fonctions de seuil. En revanche, la fonction softmax offre à la fois une interprétation probabiliste et une dérivée calculable, la rendant plus efficace pour de telles applications.

La fonction \(\argmax\) peut être appliquée a posteriori aux réseaux entraînés pour faire des prédictions de classe.

Softmax garantit que toutes les sorties d’activation se situent entre 0 et 1 et que leur somme est égale à 1.

Softmax

La fonction softmax est une fonction d’activation utilisée dans les problèmes de classification multiclasses pour convertir un vecteur de scores bruts en probabilités qui totalisent 1.

Étant donné un vecteur \(\mathbf{z} = [z_1, z_2, \ldots, z_n]\) :

\[ \sigma(\mathbf{z})_i = \frac{e^{z_i}}{\sum_{j=1}^{n} e^{z_j}} \]

où \(\sigma(\mathbf{z})_i\) est la probabilité de la classe \(i\), et \(n\) est le nombre de classes.

La fonction softmax met l’accent sur les scores les plus élevés tout en atténuant les scores les plus faibles, permettant une interprétation probabiliste des sorties.

On peut clairement voir que cette activation s’applique à l’ensemble de la couche, puisque la dénomination dépend des valeurs de tous les \(z_j\), pour \(j \in 1 \ldots n\).

1. Assure la positivité :

   La fonction exponentielle garantit que toutes les sorties sont positives, une propriété nécessaire pour des probabilités valides.

2. Amplifie les différences relatives :

   L’exponentiation est une transformation non linéaire monotone qui augmente beaucoup plus les grandes valeurs que les petites. Si un logit est légèrement plus grand, \(e^{z_i}\) devient disproportionnellement plus grand, accentuant la distribution (utile pour mettre en valeur la classe la plus probable).

3. Préserve l’ordre :

   Puisque \(e^x\) est strictement croissante, la classe avec le logit le plus élevé avant softmax reste celle avec la probabilité la plus élevée après.

4. Facilite l’apprentissage basé sur le gradient :

   L’exponentielle adoucit la transition entre les classes, fournissant des sorties différentiables et des gradients stables pour l’optimisation avec l’entropie croisée.

Un logit est une valeur de pré-activation (\(z_i\)). Chaque neurone dans la couche de sortie (avant activation) produit un logit \(z_i\).

Softmax

\(z_1\)	\(z_2\)	\(z_3\)	\(\sigma(z_1)\)	\(\sigma(z_2)\)	\(\sigma(z_3)\)	\(\sum\)
1.47	-0.39	0.22	0.69	0.11	0.20	1.00
5.00	6.00	4.00	0.24	0.67	0.09	1.00
0.90	0.80	1.10	0.32	0.29	0.39	1.00
-2.00	2.00	-3.00	0.02	0.98	0.01	1.00

1. Maintient l’ordre relatif : La fonction softmax préserve l’ordre relatif des valeurs d’entrée. Si une entrée est supérieure à une autre, sa sortie correspondante sera également supérieure.

2. Interprétée comme des probabilités : Chaque valeur se situe dans la plage de 0 à 1. Les valeurs de sortie de la fonction softmax sont normalisées pour totaliser un, ce qui permet de les interpréter comme des probabilités.

3. Différences relatives : Lorsque les différences relatives entre les valeurs d’entrée sont petites, les différences dans les probabilités de sortie restent petites, reflétant la distribution des entrées. Lorsque les valeurs d’entrée sont identiques, les sorties seront égales à \(\frac{1}{n}\), où \(n\) est le nombre de classes.

4. Large gamme de valeurs : La fonction softmax peut traiter efficacement une large gamme de valeurs d’entrée, grâce à la fonction exponentielle et à la normalisation, qui adaptent les entrées à une plage probabiliste.

Ces propriétés rendent la fonction softmax particulièrement utile pour les tâches de classification multiclasses en apprentissage automatique.

Valeurs de softmax pour un vecteur de longueur 3.

Softmax

Fonction de perte d’entropie croisée

L’entropie croisée dans une tâche de classification multiclasses pour un exemple :

\[ J(W) = -\sum_{k=1}^{K} y_k \log(\hat{y}_k) \]

Où :

• \(K\) est le nombre de classes.
• \(y_k\) est la distribution réelle pour la classe \(k\).
• \(\hat{y}_k\) est la probabilité prédite de la classe \(k\) par le modèle.

• Le vecteur cible \(y\) est exprimé comme un vecteur encodé one-hot de longueur \(K\), où l’élément correspondant à la classe réelle est fixé à 1, et tous les autres éléments sont à 0.

• Par conséquent, dans la somme sur les classes, seul le terme associé à la classe réelle contribue une valeur non nulle.

• Ainsi, la perte d’entropie croisée pour un exemple unique est donnée par \(-\log(\hat{y}_k)\), où \(\hat{y}_k\) est la probabilité prédite pour la classe réelle.

• La probabilité prédite \(\hat{y}_k\) est dérivée de la fonction softmax appliquée à la couche de sortie du réseau neuronal.

Fonction de perte d’entropie croisée

• Problème de classification : 3 classes
  • Versicolour, Setosa, Virginica.
• Encodage one-hot :
  • Setosa = \([0, 1, 0]\).
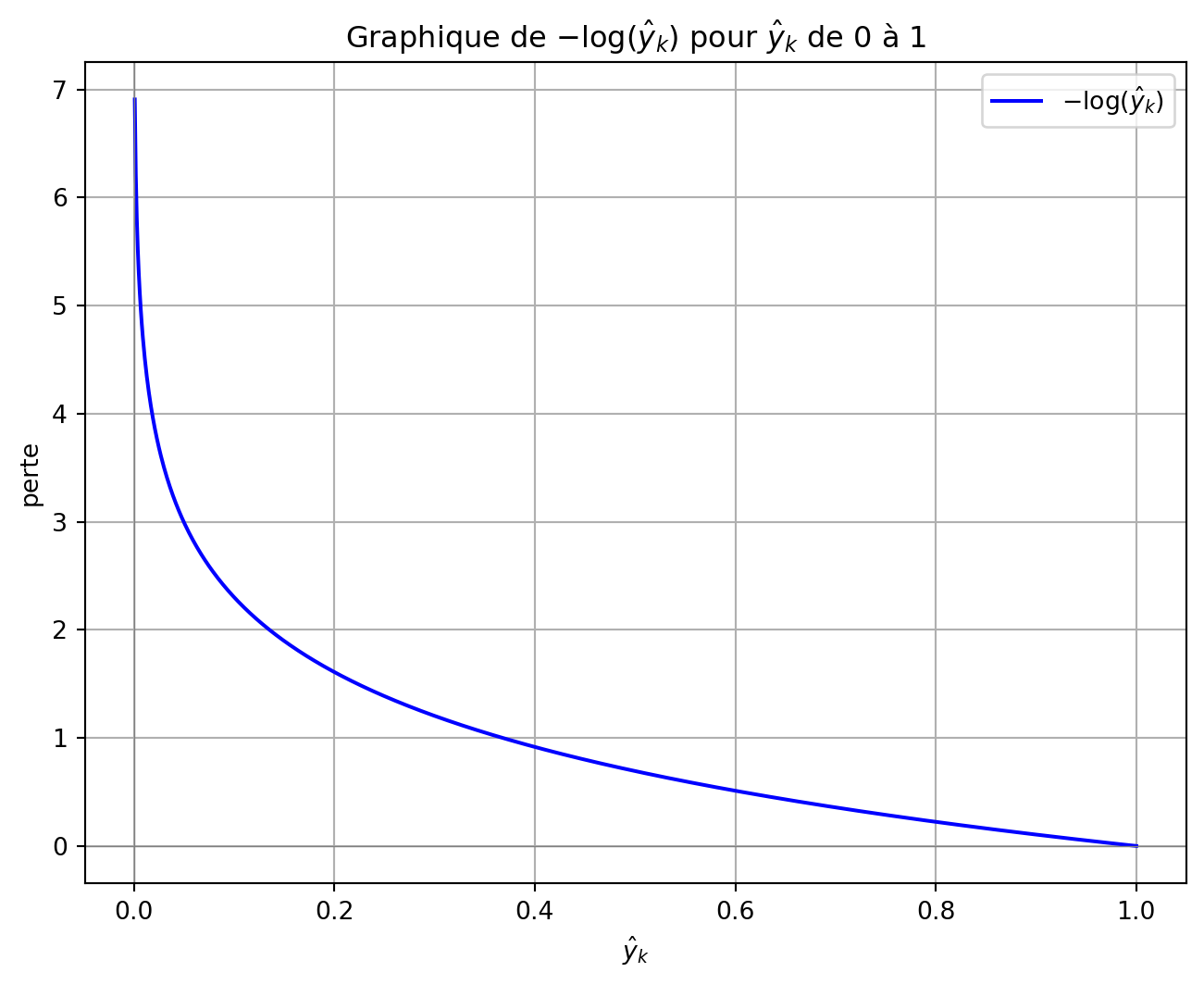
• Sorties Softmax & Perte :
  • \([0.22,\mathbf{0.7}, 0.08]\) : Perte = \(-\log(0.7) = 0.3567\).
  • \([0.7, \mathbf{0.22}, 0.08]\) : Perte = \(-\log(0.22) = 1.5141\).
  • \([0.7, \mathbf{0.08}, 0.22]\) : Perte = \(-\log(0.08) = 2.5257\).

Parmi les sorties softmax, l’entropie croisée n’évalue que la composante correspondant à \(k=1\) (Setosa), car les autres entrées dans le vecteur encodé one-hot sont nulles. Cet élément pertinent est mis en évidence en gras. Lorsque la prédiction softmax correspond étroitement à la valeur attendue, la perte résultante est minimale (0.3567). À l’inverse, lorsque la prédiction s’éloigne de la valeur attendue, la perte augmente (1.5141 et 2.5257).

Cas : un exemple

• Dans la somme, seul le terme où \(y_k = 1\) contribue une valeur non nulle.

• En raison du signe négatif précédant la somme, la valeur de la fonction est \(-\log(\hat{y}_k)\).

• Si la probabilité prédite \(\hat{y}_k\) est proche de 1, la perte approche de zéro, indiquant une pénalité minimale.

• À l’inverse, lorsque \(\hat{y}_k\) approche de 0, indiquant une mauvaise prédiction, la perte approche l’infini. Cette pénalité importante permet à la perte d’entropie croisée de converger plus rapidement que l’erreur quadratique moyenne.

Cas : ensemble de données

Pour un ensemble de données avec \(N\) exemples, la perte moyenne d’entropie croisée sur tous les exemples est calculée comme suit :

\[ L = -\frac{1}{N} \sum_{i=1}^{N} \sum_{k=1}^{K} y_{i,k} \log(\hat{y}_{i,k}) \]

Où :

• \(i\) est l’index des exemples dans l’ensemble de données.
• \(y_{i,k}\) et \(\hat{y}_{i,k}\) sont respectivement les valeurs réelles et les probabilités prédites pour la classe \(k\) de l’exemple \(i\).

Régularisation

Définition

La régularisation regroupe un ensemble de techniques visant à améliorer la capacité de généralisation d’un modèle en atténuant le surapprentissage. En décourageant une complexité excessive du modèle, ces méthodes améliorent la robustesse et la performance du modèle sur des données non vues.

Ajout de termes de pénalité à la perte

• En optimisation numérique, il est courant d’ajouter des termes supplémentaires à la fonction objectif afin de dissuader certaines caractéristiques indésirables du modèle.

• Pour un problème de minimisation, le processus d’optimisation vise à éviter des coûts élevés associés à ces termes de pénalité.

Fonction de perte

Prenons la fonction de perte de l’erreur absolue moyenne :

\[ \mathrm{MAE}(X,W) = \frac{1}{N} \sum_{i=1}^{N} | h_W(x_i) - y_i | \]

Où :

• \(W\) sont les poids de notre réseau.
• \(h_W(x_i)\) est la sortie du réseau pour l’exemple \(i\).
• \(y_i\) est la vraie étiquette pour l’exemple \(i\).

Terme(s) de pénalité

Un ou plusieurs termes peuvent être ajoutés à la perte :

\[ \mathrm{MAE}(X,W) = \frac{1}{N} \sum_{i=1}^{N} | h_W(x_i) - y_i | + \mathrm{pénalité} \]

Norme

Une norme assigne une longueur non négative à un vecteur.

La norme \(\ell_p\) d’un vecteur \(\mathbf{z} = [z_1, z_2, \ldots, z_n]\) est définie comme suit :

\[ \|\mathbf{z}\|_p = \left( \sum_{i=1}^{n} |z_i|^p \right)^{1/p} \]

Une norme est une fonction qui attribue une longueur ou taille non négative à chaque vecteur dans un espace vectoriel, en respectant certaines propriétés : positivité, multiplication scalaire, inégalité triangulaire, et le fait que la norme est nulle si et seulement si le vecteur est nul.

Avec des valeurs de \(p\) plus grandes, la norme \(\ell_p\) met de plus en plus l’accent sur les valeurs de \(z_i\) les plus grandes à cause de l’exponentiation.

Normes \(\ell_1\) et \(\ell_2\)

La norme \(\ell_1\) (norme de Manhattan) est :

\[ \|\mathbf{z}\|_1 = \sum_{i=1}^{n} |z_i| \]

La norme \(\ell_2\) (norme euclidienne) est :

\[ \|\mathbf{z}\|_2 = \sqrt{\sum_{i=1}^{n} z_i^2} \]

Régularisation \(l_1\) et \(l_2\)

Ci-dessous, \(\alpha\) et \(\beta\) déterminent le degré de régularisation appliqué ; fixer ces valeurs à zéro désactive effectivement le terme de régularisation.

\[ \mathrm{MAE}(X,W) = \frac{1}{N} \sum_{i=1}^{N} | h_W(x_i) - y_i | + \alpha \ell_1 + \beta \ell_2 \]

Recommandations

• Régularisation \(\ell_1\) :
  • Encourage la parcimonie, mettant à zéro beaucoup de poids.
  • Utile pour la sélection d’attributs en réduisant la dépendance à certains attributs.
• Régularisation \(\ell_2\) :
  • Encourage des poids petits et répartis pour la stabilité.
  • Idéal lorsque toutes les attributs contribuent et que la réduction de la complexité est primordiale.

Voir kong_and_yu-2018 pour un exemple.

Exemple Keras

import tensorflow as tf
from tensorflow.python.keras.layers import Dense

regularizer = tf.keras.regularizers.l2(0.001)

dense = Dense(50, kernel_regularizer=regularizer)

Cette couche utilise spécifiquement la régularisation \(\ell_2\), contrairement à la discussion précédente où la régularisation était appliquée globalement à l’ensemble du modèle.

Dropout

Le dropout est une technique de régularisation dans les réseaux neuronaux où des neurones sélectionnés aléatoirement sont ignorés pendant l’entraînement, réduisant ainsi le surapprentissage en empêchant la co-adaptation des attributs.

Hinton et al. (2012)

Dropout

• Lors de chaque étape d’entraînement, chaque neurone dans une couche de dropout a une probabilité \(p\) d’être exclu du calcul, des valeurs typiques de \(p\) allant de 10 % à 50 %.

• Bien que cela puisse sembler contre-intuitif, cette approche empêche le réseau de dépendre de neurones spécifiques, favorisant ainsi la distribution des représentations apprises sur plusieurs neurones.

Dropout

• Le dropout est l’une des méthodes de régularisation les plus populaires et les plus efficaces pour réduire le surapprentissage.

• L’amélioration typique des performances est modeste, généralement autour de 1 à 2 %.

Pendant l’entraînement, chaque neurone dans une couche de dropout est aléatoirement exclu (mis à zéro) avec une probabilité \(p\) — le taux de dropout.

Lorsque le dropout « met un neurone à zéro », cela signifie que pour l’étape d’entraînement en cours (mini-lot), l’activation de sortie de ce neurone est remplacée par zéro. Le neurone existe toujours dans le réseau, ses poids ne sont ni supprimés ni modifiés, mais sa sortie ne contribue en rien au passage avant ou arrière pour ce lot.

Dans le lot suivant, un nouveau masque aléatoire est échantillonné, donc un sous-ensemble différent de neurones est exclu. Au fil de nombreuses itérations, tous les neurones participent, mais jamais tous en même temps.

Lors de l’inférence, le mécanisme est désactivé, tous les neurones sont actifs.

Keras

import keras
from keras.models import Sequential
from keras.layers import InputLayer, Dropout, Flatten, Dense

model = tf.keras.Sequential([
    InputLayer(shape=[28, 28]),
    Flatten(),
    Dropout(rate=0.2),
    Dense(300, activation="relu"),
    Dropout(rate=0.2),
    Dense(100, activation="relu"),
    Dropout(rate=0.2),
    Dense(10, activation="softmax")
])

Le taux de dropout peut différer entre les couches ; des taux plus élevés peuvent être appliqués aux couches plus larges, tandis que des taux plus petits sont adaptés aux couches plus petites. Il est courant dans de nombreux réseaux d’appliquer le dropout uniquement après la dernière couche cachée.

Ajout de couches Dropout au modèle Fashion-MNIST de la dernière leçon.

Définition

L’arrêt anticipé (early stopping) est une technique de régularisation qui interrompt l’entraînement dès que la performance du modèle sur un ensemble de validation commence à se dégrader, empêchant ainsi le surapprentissage en s’arrêtant avant que le modèle n’apprenne le bruit.

Geoffrey Hinton appelle cela le “beau repas gratuit.”

Early Stopping

Attribution : Géron (2022), 04_training_linear_models.ipynb.

Prologue

Résumé

• Fonctions de perte :
  • Tâches de régression : Erreur quadratique moyenne (MSE).
  • Tâches de classification : Perte d’entropie croisée avec activation softmax pour les sorties multiclasses.
• Techniques de régularisation :
  • Régularisation L1 et L2 : Ajouter des termes de pénalité à la perte pour décourager les poids élevés.
  • Dropout : Désactiver aléatoirement des neurones pendant l’entraînement pour éviter le surapprentissage.
  • Early Stopping : Interrompre l’entraînement lorsque la performance de validation se dégrade.

Prochain cours

• Nous introduirons les réseaux convolutifs.

Références

Géron, Aurélien. 2022. Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow. 3ᵉ éd. O’Reilly Media, Inc.

Hinton, Geoffrey E., Nitish Srivastava, Alex Krizhevsky, Ilya Sutskever, et Ruslan Salakhutdinov. 2012. « Improving neural networks by preventing co-adaptation of feature detectors ». CoRR abs/1207.0580. http://arxiv.org/abs/1207.0580.

Russell, Stuart, et Peter Norvig. 2020. Artificial Intelligence: A Modern Approach. 4ᵉ éd. Pearson. http://aima.cs.berkeley.edu/.

Marcel Turcotte

Marcel.Turcotte@uOttawa.ca

École de science informatique et de génie électrique (SIGE)

Université d’Ottawa