Architectures de réseaux neuronaux

CSI 4506 - Automne 2025

Marcel Turcotte

Version: oct. 28, 2025 20h59

Préambule

Message du jour

Andrej Karpathy est un informaticien slovaquo-canadien né en 1986 à Bratislava, qui a déménagé à Toronto avec sa famille à l’âge de 15 ans. Il a obtenu un baccalauréat en informatique et en physique à l’Université de Toronto (2009) ainsi qu’une maîtrise à l’Université de la Colombie-Britannique (2011), où il a travaillé avec son directeur Michiel van de Panne sur l’apprentissage de contrôleurs pour des figures simulées physiquement. Il a ensuite complété un doctorat à l’Université Stanford sous la supervision de Fei-Fei Li, portant sur l’intersection entre la vision par ordinateur et le traitement du langage naturel.

• Membre fondateur et chercheur chez OpenAI (2015 – 2017).
• Directeur principal de l’IA et de la vision Autopilot chez Tesla, Inc. (2017 – 2022).
• Retour chez OpenAI en 2023 pour diriger une petite équipe travaillant sur l’amélioration des modèles (notamment GPT-4), avant de quitter l’entreprise en 2024.
• Fondateur de Eureka Labs (depuis 2024), une jeune entreprise axée sur l’IA et l’éducation.

Will transformers drive AI in 10 years?, Andrej Karpathy, 2025-10-27.

Objectifs d’apprentissage

• Expliquer la hiérarchie des concepts dans l’apprentissage profond
• Comparer les réseaux neuronaux profonds et peu profonds
• Décrire la structure et la fonction des réseaux neuronaux convolutifs (CNNs)
• Comprendre les opérations de convolution utilisant des noyaux
• Expliquer les champs récepteurs, le padding et le stride dans les CNNs
• Discuter du rôle et des avantages de la couche de pooling

Dans le cours précédent, nous avons examiné l’algorithme de rétropropagation, qui offre une méthode systématique pour calculer les dérivées partielles de la fonction de perte. Ce calcul est essentiel pour appliquer l’algorithme de descente de gradient, permettant ainsi l’ajustement des poids dans un réseau de neurones profond. Aujourd’hui, nous aborderons un programme intensif. Nous portons notre attention sur les réseaux de neurones convolutifs.

L’étude des réseaux convolutifs présente plusieurs niveaux de complexité. N’hésitez pas à poser des questions si vous avez besoin de clarifications.

Objectifs d’apprentissage détaillés.

1. Expliquer la hiérarchie des concepts dans l’apprentissage profond
   • Comprendre comment les modèles d’apprentissage profond construisent des représentations hiérarchiques des données.
   • Reconnaître comment cette hiérarchie réduit le besoin d’ingénierie manuelle des attributs.
2. Comparer les réseaux neuronaux profonds et peu profonds
   • Discuter des raisons pour lesquelles les réseaux profonds sont plus efficaces en termes de paramètres que les réseaux peu profonds.
   • Expliquer les avantages de la profondeur dans les architectures de réseaux neuronaux.
3. Décrire la structure et la fonction des réseaux neuronaux convolutifs (CNNs)
   • Comprendre comment les CNNs détectent des motifs locaux dans les données.
   • Expliquer comment les couches convolutionnelles réduisent le nombre de paramètres grâce au partage des poids.
4. Comprendre les opérations de convolution utilisant des noyaux
   • Décrire comment les noyaux (filtres) sont appliqués sur les données d’entrée pour réaliser des convolutions.
   • Expliquer comment les cartes de attributs sont générées à partir des opérations de convolution.
5. Expliquer les champs récepteurs, le padding, et le stride dans les CNNs
   • Définir le concept de champ récepteur dans les couches convolutionnelles.
   • Comprendre comment le padding et le stride affectent les dimensions de sortie et le calcul.
6. Discuter du rôle et des avantages des couches de pooling
   • Expliquer comment les couches de pooling réduisent les dimensions spatiales et contrôlent l’overfitting.
   • Décrire comment le pooling introduit une invariance de translation dans les CNNs.

Que voyez-vous ?

import numpy as np
import matplotlib.pyplot as plt
from skimage import data, transform
from skimage.util import img_as_float

# Charger une image échantillon (Chelsea le chat)
image = img_as_float(data.chelsea())

# Définir les transformations
def translate(image, tx=50, ty=30):
    tform = transform.AffineTransform(translation=(tx, ty))
    return transform.warp(image, tform.inverse)

def rotate(image, angle=30):
    return transform.rotate(image, angle, resize=True)

def shear(image, shear_deg=15):
    shear_rad = np.deg2rad(shear_deg)
    tform = transform.AffineTransform(shear=shear_rad)
    return transform.warp(image, tform.inverse)

# Appliquer les transformations
rotated = rotate(image, 30)
translated = translate(image, 60, 30)
sheared = shear(image, 15)

# Créer une grille 2x2
fig, axes = plt.subplots(2, 2, figsize=(5, 5))
axes = axes.ravel()
titles = ['Original', 'Tourné (30°)', 'Translaté (60, 30)', 'Cisaillé (15°)']
images = [image, rotated, translated, sheared]

for ax, img, title in zip(axes, images, titles):
    ax.imshow(img)
    ax.set_title(title)
    ax.axis('off')

plt.tight_layout()
plt.show()

Même si ces images semblent très différentes dans l’espace des pixels, vous pouvez toujours reconnaître le chat. Un réseau neuronal convolutionnel apprend des filtres qui sont robustes à ces transformations — c’est pourquoi il est si puissant pour les tâches de vision.

Convolution

Hiérarchie des concepts

Dans le livre “Deep Learning” (Goodfellow, Bengio, et Courville 2016), les auteurs Goodfellow, Bengio, et Courville définissent l’apprentissage profond comme un sous-ensemble de l’apprentissage automatique permettant aux ordinateurs de “comprendre le monde en termes d’une hiérarchie de concepts”.

Cette approche hiérarchique est l’une des contributions les plus significatives de l’apprentissage profond. Elle réduit le besoin d’ingénierie manuelle des attributs et recentre l’attention sur l’ingénierie des architectures de réseaux neuronaux.

Les réseaux de neurones convolutifs (CNN) ont eu un impact profond sur le domaine de l’apprentissage automatique, en particulier dans les domaines du traitement d’images et de vidéos.

1. Révolution de la reconnaissance d’images : Les CNN ont considérablement fait progresser l’état de l’art en matière de reconnaissance et de classification d’images, atteignant une haute précision sur divers ensembles de données. Cela a conduit à des percées dans des domaines tels que l’imagerie médicale, les véhicules autonomes et la reconnaissance faciale.

2. Extraction de caractéristiques : Les CNN apprennent automatiquement à extraire des caractéristiques à partir de données brutes, éliminant ainsi le besoin d’ingénierie manuelle des caractéristiques. Cette capacité a été cruciale pour traiter des motifs de données complexes et a élargi l’applicabilité de l’apprentissage automatique à divers domaines.

3. Apprentissage par transfert : Les CNN facilitent l’apprentissage par transfert, où des réseaux pré-entraînés sur de grands ensembles de données peuvent être ajustés pour des tâches spécifiques avec des données limitées. Cela a rendu les CNN accessibles et efficaces pour un large éventail d’applications au-delà de leur champ de formation initial.

4. Avancées en apprentissage profond : Le succès des CNN a stimulé la recherche dans les architectures d’apprentissage profond, inspirant le développement de modèles plus sophistiqués tels que les réseaux de neurones récurrents (RNN), les réseaux de mémoire à long terme (LSTM) et les modèles de transformateurs.

5. Domaines d’application étendus : Au-delà du traitement d’images, les CNN ont été adaptés au traitement du langage naturel, au traitement audio, et même en bio-informatique pour des tâches telles que la prédiction de structures protéiques et la génomique.

6. Implications pour les applications du monde réel : Les CNN ont permis des applications pratiques dans des domaines tels que la santé, où ils aident à l’imagerie diagnostique, et la sécurité, où ils améliorent les systèmes de surveillance. Ils ont également contribué aux avancées en réalité virtuelle, dans le jeu vidéo et en réalité augmentée.

Nous avons exploré les algorithmes des k plus proches voisins ainsi que les arbres de décision afin de vous offrir une perspective élargie sur l’apprentissage automatique, qui ne se limite pas uniquement aux réseaux de neurones. Actuellement, nous étudions les réseaux de neurones convolutifs pour illustrer la diversité des architectures existantes dans ce domaine. Bien qu’il soit impossible de couvrir tous les aspects en détail, notre objectif est de vous fournir une compréhension solide des différents paradigmes de l’apprentissage automatique.

Attribution: LeCun, Bengio, et Hinton (2015)

Hiérarchie des concepts

• Chaque couche détecte des motifs à partir de la sortie de la couche précédente.
  • En d’autres termes, en progressant de l’entrée à la sortie du réseau, le réseau découvre des “motifs de motifs”.
    • En analysant une image, les réseaux détectent d’abord des motifs simples, tels que des lignes verticales, horizontales, diagonales, des arcs, etc.
    • Ceux-ci sont ensuite combinés pour former des coins, des croix, etc.
• (Cela explique comment fonctionne l’apprentissage par transfert et pourquoi il est pertinent de ne sélectionner que les couches inférieures.)

Mais aussi…

“Un MLP avec une seule couche cachée peut théoriquement modéliser même les fonctions les plus complexes, à condition qu’il dispose d’assez de neurones. Mais pour des problèmes complexes, les réseaux profonds ont une efficacité paramétrique bien plus élevée que les réseaux peu profonds : ils peuvent modéliser des fonctions complexes en utilisant exponentiellement moins de neurones que les réseaux peu profonds, leur permettant d’atteindre de bien meilleures performances avec la même quantité de données d’entraînement.”

Géron (2019) § 10

Combien de couches ?

• Commencez avec une seule couche, puis augmentez le nombre de couches jusqu’à ce que le modèle commence à sur-apprendre les données d’entraînement.
• Ajustez finement le modèle en ajoutant des techniques de régularisation (couches de dropout, termes de régularisation, etc.).

Le nombre de neurones et autres hyperparamètres sont déterminés à l’aide d’une recherche par grille.

Observation

Prenons un réseau de neurones feed-forward (FFN) et son modèle :

\[ h_{W,b}(X) = \phi_k(\ldots \phi_2(\phi_1(X)) \ldots) \]

où

\[ \phi_l(Z) = \sigma(W_l Z + b_l) \]

pour \(l=1 \ldots k\). - Le nombre de paramètres augmente rapidement :

\[ (\text{taille de la couche}_{l-1} + 1) \times \text{taille de la couche}_{l} \]

Deux couches de 1 000 unités impliquent 1 000 000 paramètres !

Tâche de classification d’Images

• Considérons une image RGB de dimensions \(224 \times 224\), ce qui est relativement petit selon les critères contemporains.

• L’image est composée de \(224 \times 224 \times 3 = 150,528\) attributs d’entrée.

• Un réseau de neurones avec seulement une couche dense cachée unique nécessiterait plus de 22,658,678,784 (22 milliards) de paramètres, soulignant la complexité computationnelle impliquée.

Réseau neuronal convolutif (CNN)

Un excellent aperçu des CNNs à haut niveau.

Réseau neuronal convolutif (CNN)

• Les informations cruciales sur les motifs sont souvent locales.

  • Par exemple, les arêtes, coins, croix.

• Les couches convolutionnelles réduisent significativement les paramètres.

  • Contrairement aux couches denses, les neurones dans une couche convolutionnelle ne sont pas complètement connectés à la couche précédente.

  • Les neurones ne se connectent qu’à leurs champs récepteurs (zones rectangulaires).

Les réseaux convolutionnels proviennent du domaine de la vision par ordinateur, ce qui explique leur compatibilité intrinsèque avec les entrées structurées en grille.

La publication originale de Yann Lecun a été citée près de 35 000 fois (Lecun et al. 1998)

Noyau

Noyau

Le processus computationnel détaillé sera élaboré par la suite. À ce stade, il suffit de noter que le noyau est systématiquement parcouru à travers la matrice d’entrée, générant une sortie distincte à chaque itération.

Un noyau (kernel) est une petite matrice, généralement de taille \(3 \times 3\), \(5 \times 5\), ou similaire, qui glisse sur les données d’entrée (comme une image) pour effectuer la convolution.

Noyau

Au départ, le noyau est positionné pour chevaucher le coin supérieur gauche de la matrice d’entrée.

Noyau

Il peut être déplacé vers la droite trois fois.

Noyau

Noyau

Noyau

Il se déplace ensuite sur la deuxième rangée. On peut alors le déplacer à nouveau trois fois.

Déplacer le noyau

Noyau

Avec le noyau placé sur une région spécifique de la matrice d’entrée, la convolution consiste en une multiplication élément par élément (chaque élément du noyau est multiplié par l’élément correspondant de la région de la matrice d’entrée qu’il chevauche), suivie d’une sommation des résultats pour produire une valeur scalaire unique.

Noyau

\(1 \times 1 + 2 \times 0 + 3 \times (-1) + 6 \times 1 + 5 \times 0 + 4 \times (-1) + 1 \times 1 + 2 \times 0 + 3 \times (-1) = -2\)

Noyau

On parle de carte d’attributs parce que ces sorties servent d’attributs pour la couche suivante. Dans les CNN, le terme “carte d’attributs’” désigne la sortie d’une couche de convolution après l’application de filtres aux données d’entrée. Ces cartes d’attributs capturent divers motifs ou attributs de l’entrée, tels que les contours ou les textures dans les données d’image.

Les cartes des attributs produites par une couche deviennent l’entrée de la couche suivante, servant ainsi d’attributs que cette dernière peut utiliser pour apprendre des motifs plus complexes. Ce processus hiérarchique d’extraction d’attributs est une caractéristique clé des CNN, leur permettant de construire progressivement des représentations plus abstraites et de haut niveau des données d’entrée à mesure que la profondeur du réseau augmente.

Les 16 valeurs résultantes peuvent être organisées dans une matrice de sortie. L’élément à la position (0,0) de cette matrice de sortie représente le résultat de l’application de l’opération de convolution avec le noyau à la position initiale sur la matrice d’entrée. Dans les réseaux neuronaux convolutifs, la matrice de sortie est appelée carte de attributs (feature map).

Floutage

import numpy as np
from PIL import Image
import matplotlib.pyplot as plt
from scipy.ndimage import convolve

def apply_kernel_to_image(image_path, kernel):
    # Charger l'image et la convertir en niveaux de gris
    image = Image.open(image_path).convert('L')
    image_array = np.array(image)

    # Appliquer la convolution en utilisant le noyau fourni
    convolved_array = convolve(image_array, kernel, mode='reflect')

    # Convertir le tableau convolué en image
    convolved_image = Image.fromarray(convolved_array)

    # Afficher l'image originale et convoluée
    plt.figure(figsize=(10, 4))

    plt.subplot(1, 2, 1)
    plt.title('Image originale')
    plt.imshow(image_array, cmap='gray')
    plt.axis('off')

    plt.subplot(1, 2, 2)
    plt.title('Image convoluée')
    plt.imshow(convolved_image, cmap='gray')
    plt.axis('off')

    plt.tight_layout()
    plt.show()

# Définir le noyau de moyenne 3x3
kernel = np.array([
    [1/9, 1/9, 1/9],
    [1/9, 1/9, 1/9],
    [1/9, 1/9, 1/9]
])

# Appliquer le noyau à l'image (spécifiez le chemin de l'image)
image_path = '../../assets/images/uottawa_hor_black.png'
apply_kernel_to_image(image_path, kernel)

# Define the 3x3 averaging kernel

kernel = np.array([
    [1/9, 1/9, 1/9],
    [1/9, 1/9, 1/9],
    [1/9, 1/9, 1/9]
])

L’application de noyaux aux images est une pratique de longue date dans le domaine du traitement d’images.

Un pixel est transformé en la moyenne de lui-même et de ses huit voisins environnants, ce qui crée un effet de flou (blurring) sur l’image.

Détection des bords verticaux

# Définir le noyau de détection des bords verticaux 3x3

kernel = np.array([
    [-0.25, 0, 0.25],
    [-0.25, 0, 0.25],
    [-0.25, 0, 0.25]
])

Il s’agit d’un type de noyau de détection de contours, spécifiquement un filtre de gradient horizontal ou un opérateur de Sobel. Il est conçu pour détecter les changements d’intensité le long de l’axe horizontal, en mettant en évidence les contours verticaux dans une image.

Lorsque ce noyau est convolué avec une image :

• Il met en évidence les contours verticaux en calculant la différence d’intensité des pixels entre les côtés gauche et droit d’un point.
• Les valeurs négatives (-1) à gauche soustraient de l’intensité, tandis que les valeurs positives (1) à droite ajoutent de l’intensité, mesurant ainsi effectivement le gradient horizontal.
• Les zéros au milieu ignorent la contribution du pixel central, se concentrant uniquement sur le contraste entre les voisins gauche et droit.

Le résultat est une image où :

• Les contours verticaux (par exemple, la frontière entre un objet sombre et un fond clair) apparaissent lumineux ou sombres, selon la direction du changement d’intensité.
• Les contours horizontaux ou les zones uniformes ont tendance à être supprimés (proches de zéro).

Imaginez glisser ce noyau sur une image comme un scanner. Pour chaque pixel :

• Il regarde les pixels à sa gauche (en soustrayant leur valeur avec -1) et à sa droite (en ajoutant leur valeur avec 1).

• Si les côtés gauche et droit sont similaires (par exemple, même couleur), le résultat est proche de zéro (pas de contour).

• Si la gauche est sombre et la droite est claire (ou vice versa), le résultat est une valeur positive ou négative forte, montrant un contour vertical.

Cela est utile en vision par ordinateur (comme dans les CNNs de Tesla) pour aider à détecter les contours d’objets ou les lignes de voie en mettant en évidence où les valeurs des pixels changent fortement dans la direction horizontale.

Ce noyau détecte les bords verticaux en accentuant les différences d’intensité entre les colonnes adjacentes. Il soustrait les valeurs des pixels de gauche de celles de droite, améliorant ainsi les transitions verticales tout en supprimant les régions uniformes.

Détection des bords horizontaux

# Définir le noyau de détection des bords horizontaux 3x3

kernel = np.array([
    [-0.25, -0.25, -0.25],
    [0, 0, 0],
    [0.25, 0.25, 0.25]
])

Ce noyau détecte les bords horizontaux en mettant en évidence les différences d’intensité entre les lignes adjacentes. Il soustrait les valeurs des pixels de la ligne supérieure de celles de la ligne inférieure, accentuant les transitions horizontales tout en minimisant les zones uniformes.

Traitement d’images

Utilise le langage de programmation Julia.

Mais qu’est-ce qu’une convolution ?

Convolution au-delà de son application dans le traitement d’images.

Noyaux

Contrairement au traitement d’images, où les noyaux sont définis manuellement par l’utilisateur, dans le cas des réseaux convolutifs, les noyaux sont automatiquement appris par le réseau.

À suivre \(\ldots\)

Champ récepteur

Champ récepteur

Attribution: Géron (2019) Figure 14.2

Champ récepteur

• Chaque unité est connectée aux neurones de ses champs récepteurs.
  • L’unité \(i,j\) dans la couche \(l\) est connectée aux unités de \(i\) à \(i+f_h-1\), \(j\) à \(j+f_w-1\) de la couche \(l-1\), où \(f_h\) et \(f_w\) sont respectivement la hauteur et la largeur du champ récepteur.

Padding

Zero padding. Pour conserver des couches de même taille, la grille peut être remplie de zéros.

Padding

Pas de padding

Padding moitié

Padding complet

Attribution: github.com/vdumoulin/conv_arithmetic

Stride

Stride. Il est possible de connecter une couche \((l-1)\) plus grande à une couche \((l)\) plus petite en sautant des unités. Le nombre d’unités sautées est appelé stride, \(s_h\) et \(s_w\).

• L’unité \(i,j\) dans la couche \(l\) est connectée aux unités de \(i \times s_h\) à \(i \times s_h + f_h - 1\), \(j \times s_w\) à \(j \times s_w + f_w - 1\) de la couche \(l-1\), où \(f_h\) et \(f_w\) sont respectivement la hauteur et la largeur du champ récepteur, \(s_h\) et \(s_w\) sont respectivement la hauteur et la largeur du stride.

Stride

Pas de padding, stride

Padding, stride

Attribution: github.com/vdumoulin/conv_arithmetic

Filtres

Filtres

• Une fenêtre de taille \(f_h \times f_w\) est déplacée sur la sortie des couches \(l-1\), appelée carte de attributs d’entrée, position par position.

• Pour chaque emplacement, le produit est calculé entre la partie extraite et une matrice de la même taille, appelée noyau convolutionnel ou filtre. La somme des valeurs dans la matrice résultante constitue la sortie pour cet emplacement.

Modèle

Modèle

\[ z_{i,j,k} = b_k + \sum_{u=0}^{f_h-1} \sum_{v=0}^{f_w-1} \sum_{k'=0}^{f_{n'}-1} x_{i',j',k'} \cdot w_{u,v,k',k} \]

où \(i' = i \times s_h + u\) et \(j' = j \times s_w + v\).

Attribution: Géron (2019) Figure 14.6

Couche convolutionnelle

• “Ainsi, une couche remplie de neurones utilisant le même filtre produit une carte de d’attributs.”

• “Bien sûr, il n’est pas nécessaire de définir les filtres manuellement : au lieu de cela, pendant l’entraînement, la couche convolutionnelle apprendra automatiquement les filtres les plus utiles pour sa tâche.”

Géron (2019) § 14

Couche convolutionnelle

• “(…) et les couches supérieures apprendront à les combiner en des motifs plus complexes.”

• “Le fait que tous les neurones d’une carte d’attributs partagent les mêmes paramètres réduit considérablement le nombre de paramètres du modèle.”

Géron (2019) § 14

Résumé

1. Carte d’attributs (feature map) : Dans les réseaux neuronaux convolutifs (CNNs), la sortie d’une opération de convolution est appelée une carte d’attributs. Elle capture les attributs de l’entrée sous une forme simplifiée et localisée par rapport au filtre appliqué.

Résumé

2. Paramètres du noyau : Les paramètres du noyau sont appris via le processus de rétropropagation, permettant au réseau d’optimiser ses capacités d’extraction d’attributs en fonction des données d’entraînement.

Résumé

3. Terme de biais : Un seul terme de biais est ajouté uniformément à toutes les entrées de la carte d’attributs. Ce biais aide à ajuster le niveau d’activation, offrant une flexibilité supplémentaire au réseau pour mieux ajuster les données.

Résumé

4. Fonction d’activation : Après l’ajout du biais, les valeurs de la carte d’attributs passent généralement par une fonction d’activation, telle que ReLU (Rectified Linear Unit). La fonction ReLU introduit une non-linéarité en mettant à zéro les valeurs négatives tout en conservant les valeurs positives, permettant ainsi au réseau d’apprendre des motifs plus complexes.

Pooling

Pooling

• Une couche de pooling présente des similitudes avec une couche convolutionnelle.

  • Chaque neurone dans une couche de pooling est connecté à un ensemble de neurones au sein d’un champ récepteur.

• Cependant, contrairement aux couches convolutionnelles, les couches de pooling ne possèdent pas de poids.

  • Elles produisent plutôt une sortie en appliquant une fonction d’agrégation, généralement maximale ou moyenne.

Dans une couche de pooling, en particulier le max pooling, la fonction max est intrinsèquement non différentiable car elle implique de sélectionner la valeur maximale parmi un ensemble d’entrées. Cependant, dans le contexte de la rétropropagation dans les réseaux de neurones, nous pouvons contourner ce problème en utilisant un concept connu sous le nom de “gradient de la fonction max”.

Voici comment cela fonctionne :

1. Passage avant : Lors du passage avant, la couche de max pooling sélectionne la valeur maximale de chaque région de pooling (par exemple, une fenêtre 2x2) et transmet ces valeurs à la couche suivante.

2. Rétropropagation : Lors de la rétropropagation, le gradient est propagé uniquement à l’entrée qui correspondait à la valeur maximale lors du passage avant. Cela signifie que la dérivée est 1 pour la position qui détenait la valeur maximale et 0 pour toutes les autres positions dans la fenêtre de pooling.

Cette approche permet effectivement à l’opération max de participer aux processus d’optimisation basés sur le gradient, comme la rétropropagation, même si la fonction max elle-même est non différentiable. En assignant le gradient à la position de la valeur maximale, le réseau peut apprendre quelles caractéristiques sont les plus importantes pour la tâche à accomplir.

Comme pour les couches convolutionnelles, les couches de pooling permettent de spécifier la taille du champ récepteur, le padding et le stride. Pour la fonction MaxPool2D, la taille par défaut du champ récepteur est \(2 \times 2\).

Pooling

• Ce processus de sous-échantillonnage conduit à une réduction de la taille du réseau ; chaque fenêtre de dimensions \(f_h \times f_w\) est condensée en une seule valeur, généralement le maximum ou la moyenne de cette fenêtre.

• Selon Géron (2019), une couche de pooling max offre un certain degré d’invariance aux petites translations (§ 14).

Pooling

1. Réduction dimensionnelle : Les couches de pooling réduisent les dimensions spatiales (largeur et hauteur) des cartes d’attributs d’entrée. Cette réduction diminue le nombre de paramètres et la charge computationnelle dans le réseau, ce qui peut aider à prévenir le sur-apprentissage.

Pooling

2. Extraction des attratributs : En résumant la présence d’attributs dans une région, les couches de pooling permettent de conserver les informations les plus critiques tout en éliminant les détails moins importants. Ce processus permet au réseau de se concentrer sur les attributs les plus saillantes.

Pooling

3. Invariance à la translation : Le pooling introduit un degré d’invariance aux translations et distorsions dans l’entrée. Par exemple, le max pooling capture la caractéristique la plus marquante dans une région locale, rendant le réseau moins sensible aux petits décalages ou variations dans l’entrée.

Pooling

4. Réduction du bruit : Le pooling peut aider à lisser le bruit dans l’entrée en agrégeant l’information sur une région, mettant ainsi en évidence les attributs cohérents par rapport aux variations aléatoires.

Pooling

5. Apprentissage hiérarchique des attributs : En réduisant progressivement les dimensions spatiales à travers les couches, les couches de pooling permettent au réseau de construire une représentation hiérarchique des données d’entrée, capturant des attributs de plus en plus abstraites et complexes à des couches plus profondes.

Keras

import tensorflow as tf
from functools import partial  

DefaultConv2D = partial(tf.keras.layers.Conv2D, kernel_size=3, padding="same", activation="relu", kernel_initializer="he_normal") 

model = tf.keras.Sequential([     
  DefaultConv2D(filters=64, kernel_size=7, input_shape=[28, 28, 1]), 
  tf.keras.layers.MaxPool2D(),     
  DefaultConv2D(filters=128),
  DefaultConv2D(filters=128),
  tf.keras.layers.MaxPool2D(),
  DefaultConv2D(filters=256),
  DefaultConv2D(filters=256),
  tf.keras.layers.MaxPool2D(),
  tf.keras.layers.Flatten(),
  tf.keras.layers.Dense(units=128, activation="relu", kernel_initializer="he_normal"),     
  tf.keras.layers.Dropout(0.5),
  tf.keras.layers.Dense(units=64, activation="relu", kernel_initializer="he_normal"),
  tf.keras.layers.Dropout(0.5),
  tf.keras.layers.Dense(units=10, activation="softmax") ])  

model.summary()

Le modèle précédemment discuté, qui comprenait des couches entièrement connectées (Dense), atteignait une précision de test de 88%.

Nous allons maintenant examiner le pooling.

Géron (2022) Chapitre 11, précision de test de 92% sur le jeu de données Fashion-MNIST

Keras

Model: "sequential"

┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type)                    ┃ Output Shape           ┃       Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ conv2d (Conv2D)                 │ (None, 28, 28, 64)     │         3,200 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ max_pooling2d (MaxPooling2D)    │ (None, 14, 14, 64)     │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ conv2d_1 (Conv2D)               │ (None, 14, 14, 128)    │        73,856 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ conv2d_2 (Conv2D)               │ (None, 14, 14, 128)    │       147,584 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ max_pooling2d_1 (MaxPooling2D)  │ (None, 7, 7, 128)      │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ conv2d_3 (Conv2D)               │ (None, 7, 7, 256)      │       295,168 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ conv2d_4 (Conv2D)               │ (None, 7, 7, 256)      │       590,080 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ max_pooling2d_2 (MaxPooling2D)  │ (None, 3, 3, 256)      │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ flatten (Flatten)               │ (None, 2304)           │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense (Dense)                   │ (None, 128)            │       295,040 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dropout (Dropout)               │ (None, 128)            │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_1 (Dense)                 │ (None, 64)             │         8,256 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dropout_1 (Dropout)             │ (None, 64)             │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_2 (Dense)                 │ (None, 10)             │           650 │
└─────────────────────────────────┴────────────────────────┴───────────────┘

 Total params: 1,413,834 (5.39 MB)

 Trainable params: 1,413,834 (5.39 MB)

 Non-trainable params: 0 (0.00 B)

Réseaux neuronaux convolutifs

L’architecture consiste à empiler séquentiellement plusieurs couches convolutionnelles, chacune suivie d’une couche d’activation ReLU, puis d’une couche de pooling. Au fur et à mesure que ce processus se poursuit, les dimensions spatiales de la représentation de l’image diminuent. En parallèle, le nombre de cartes de caractéristiques augmente, comme illustré dans notre exemple Keras. Au sommet de cette pile, un réseau de neurones entièrement connecté est intégré.

AlexNet

Krizhevsky, Sutskever, et Hinton (2012)

AlexNet se compose de huit couches avec des paramètres apprenables : cinq couches de convolution suivies de trois couches entièrement connectées. L’architecture comprend également des couches de max-pooling, des fonctions d’activation ReLU et un dropout pour améliorer les performances d’entraînement et réduire le surapprentissage.

Attribution: Prince (2023)

VGG

Simonyan et Zisserman (2015)

Des informations complémentaires se trouvent sur ce site.

Convolutional networks (ConvNets) currently set the state of the art in visual recognition. The aim of this project is to investigate how the ConvNet depth affects their accuracy in the large-scale image recognition setting.

Our main contribution is a rigorous evaluation of networks of increasing depth, which shows that a significant improvement on the prior-art configurations can be achieved by increasing the depth to 16-19 weight layers, which is substantially deeper than what has been used in the prior art. To reduce the number of parameters in such very deep networks, we use very small 3×3 filters in all convolutional layers (the convolution stride is set to 1). Please see our publication for more details.

Attribution: Prince (2023)

Performance des ConvNets

Attribution: Prince (2023)

StatQuest

La vidéo présente un exemple simple différenciant les images de la lettre O et de la lettre X, en utilisant un seul filtre. Cela simplifie l’explication et la rend facile à suivre. En pratique, cependant, chaque couche convolutionnelle contient généralement des dizaines voire des centaines de filtres.

Dernier mot

Comme vous pouvez l’imaginer, le nombre de couches et de filtres sont des hyperparamètres qui sont optimisés par le biais de l’ajustement des hyperparamètres.

Attribution: @stefaan_cotteni

Prologue

Résumé

• Hiérarchie des concepts en apprentissage profond
• Noyaux et opérations de convolution
• Champ récepteur, remplissage (padding) et pas (stride)
• Filtres et cartes des attributs
• Couches convolutionnelles
• Couches de pooling

Résumé

• Hiérarchie des concepts en apprentissage profond
  • Les modèles d’apprentissage profond représentent les données à travers des couches d’abstraction croissante.
  • Chaque couche apprend des motifs basés sur les sorties des couches précédentes (“motifs de motifs”).
  • Cet apprentissage hiérarchique réduit la dépendance à l’ingénierie manuelle des attributs.
  • Les réseaux profonds atteignent de meilleures performances avec moins de paramètres par rapport aux réseaux peu profonds.
• Réseaux de neurones convolutionnels (CNN)
  • Les CNN se spécialisent dans le traitement des données avec une topologie en grille (par ex., images).
  • Ils détectent des motifs locaux en utilisant des couches de convolution avec des poids partagés.
  • Les neurones dans les couches de convolution se connectent uniquement dans leurs champs récepteurs, et ne sont pas entièrement connectés.
  • Cette connectivité locale et le partage des poids réduisent considérablement le nombre de paramètres.
• Noyaux et opérations de convolution
  • Les noyaux (filtres) sont de petites matrices qui glissent sur les données d’entrée pour effectuer des convolutions.
  • L’opération de convolution implique une multiplication élément par élément et une sommation.
  • Les noyaux peuvent être conçus pour détecter des attributs spécifiques comme les contours et les textures.
  • Des cartes de attributs sont générées, mettant en évidence où certaines attributs sont détectées dans l’entrée.
• Champ récepteur, remplissage (padding) et pas (stride)
  • Champ récepteur : La région locale de l’entrée à laquelle un neurone est sensible.
  • Remplissage (padding) : Ajout de zéros autour de l’entrée pour maintenir les dimensions spatiales après convolution.
  • Pas (stride) : La taille de l’étape avec laquelle le noyau se déplace sur les données d’entrée.
  • Ces paramètres contrôlent la taille de sortie et le calcul dans les couches de convolution.
• Filtres et cartes d’attributs
  • Les filtres sont appris pendant l’entraînement et sont essentiels pour la détection des attributs.
  • Tous les neurones dans une carte d’attributs partagent les mêmes paramètres de filtre.
  • Ce partage conduit à une utilisation efficace des paramètres et à une détection cohérente des attributs dans l’entrée.
• Couches convolutionnelles
  • Effectuent des convolutions suivies de l’ajout d’un terme de biais et de l’application d’une fonction d’activation (par ex., ReLU).
  • La fonction d’activation introduit une non-linéarité, permettant au réseau d’apprendre des motifs complexes.
  • L’utilisation de poids et de biais partagés réduit le nombre total de paramètres.
• Couches de pooling
  • But : Réduire les dimensions spatiales des cartes de attributs pour contrôler le surapprentissage et le calcul.
  • Types :
    • Max pooling : Prend la valeur maximale dans une fenêtre de pooling.
    • Average pooling : Calcule la valeur moyenne dans une fenêtre de pooling.
  • Avantages :
    • La réduction dimensionnelle conduit à moins de paramètres et à un calcul plus rapide.
    • Introduit une invariance à la translation, rendant le réseau robuste aux décalages et distorsions.
• Construction d’architectures CNN
  • Les CNN sont construits en empilant des couches de convolution et de pooling.
  • Les dimensions spatiales diminuent tandis que le nombre de cartes d’attributs augmente dans les couches plus profondes.
  • Se termine souvent par des couches entièrement connectées pour les tâches de classification.
  • Des architectures d’exemple peuvent être implémentées en utilisant des frameworks comme Keras.
• Réglage des hyperparamètres
  • Les hyperparamètres clés incluent le nombre de couches, de filtres, de tailles de noyaux, de pas et de remplissage.
  • Un réglage approprié est essentiel pour atteindre des performances optimales du modèle.
  • Le surapprentissage peut être contrôlé en utilisant des techniques comme le dropout et la régularisation.
• Directions futures
  • Attribution de attributs :
    • Essentielles pour les applications nécessitant une explicabilité (par ex., voitures autonomes).
  • Apprentissage par transfert :
    • Implique l’utilisation de modèles pré-entraînés pour de nouvelles tâches afin d’économiser du temps et des ressources.
    • Particulièrement utile lorsque les données annotées sont rares.

Directions futures

Lors de l’intégration des CNN dans vos projets, envisagez d’explorer les sujets suivants :

• Attribution de attributs : Diverses techniques sont disponibles pour visualiser ce que le réseau a appris. Par exemple, dans le contexte des voitures autonomes, il est crucial de s’assurer que le réseau se concentre sur des attributs pertinents, évitant les distractions.

• Apprentissage par transfert : Cette approche permet la réutilisation des poids de réseaux pré-entraînés, ce qui accélère le processus d’apprentissage, réduit les besoins en calcul et facilite l’entraînement du réseau même avec un nombre limité d’exemples.

Il existe aussi des convultion 1D. Elles trouvent souvent leurs applications en bio-informatique.

Lectures Complémentaires

• Understanding Deep Learning (Prince 2023) est un manuel récemment publié qui se concentre sur les concepts fondamentaux de l’apprentissage profond.

• Il commence par les principes de base et s’étend à des sujets contemporains tels que les transformateurs, les modèles de diffusion, les réseaux de neurones graphiques, les autoencodeurs, les réseaux adversariaux et l’apprentissage par renforcement.

• Le manuel vise à aider les lecteurs à comprendre ces concepts sans entrer excessivement dans les détails théoriques.

• Il comprend soixante-huit exercices sous forme de cahiers Python.

• Le livre suit un modèle “lire d’abord, payer plus tard”.

Ressources

• Un guide de l’arithmétique de convolution pour l’apprentissage profond
• Auteurs : Vincent Dumoulin et Francesco Visin
• Dernière révision : 11 janvier 2018
  • arXiv:1603.07285
  • Dépôt GitHub

Prochain cours

• Nous introduirons les espaces de solutions.

Références

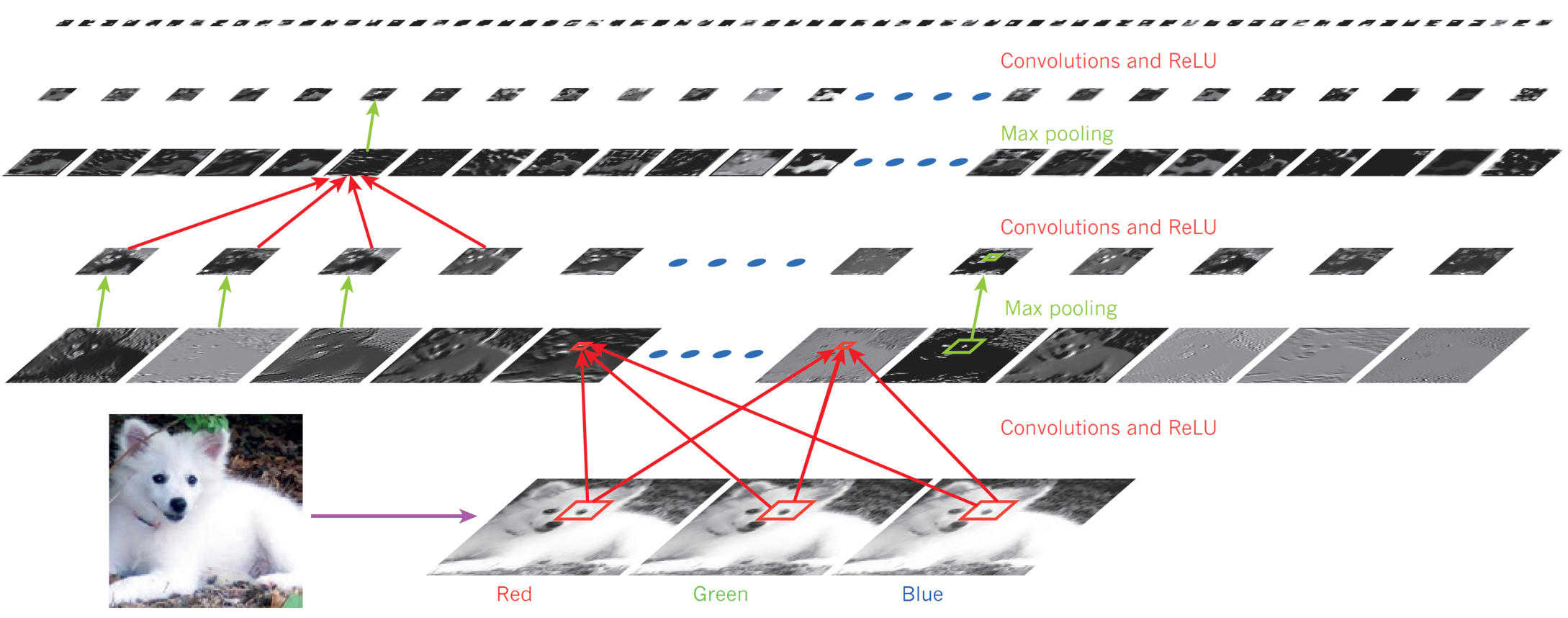
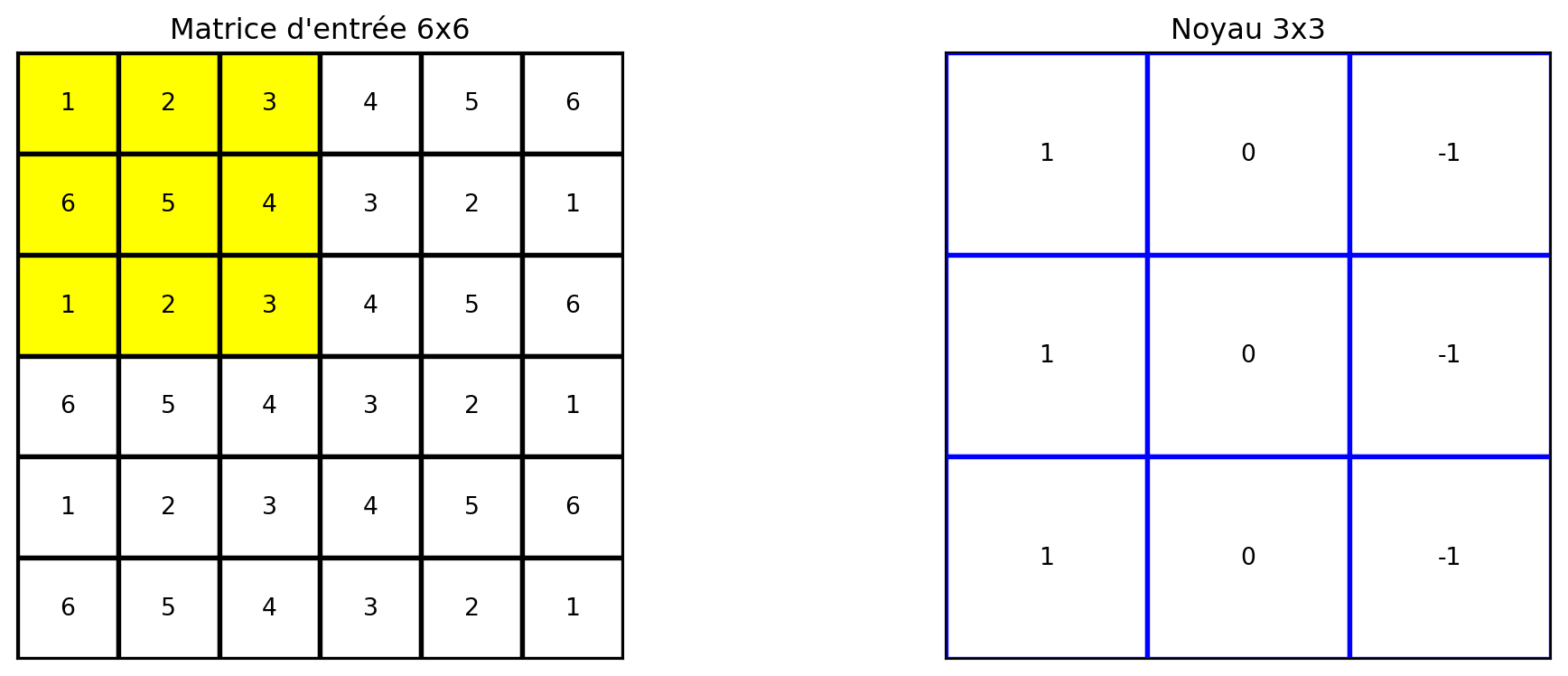
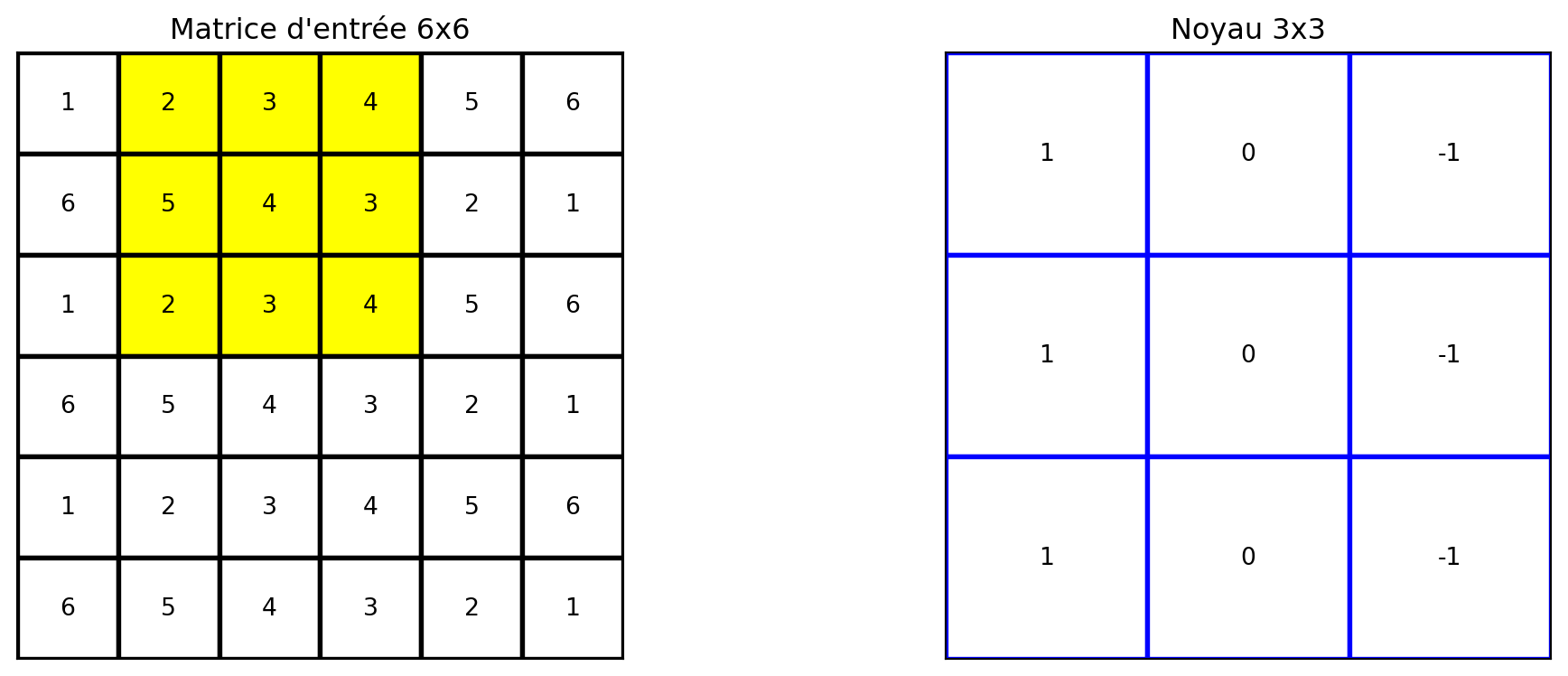
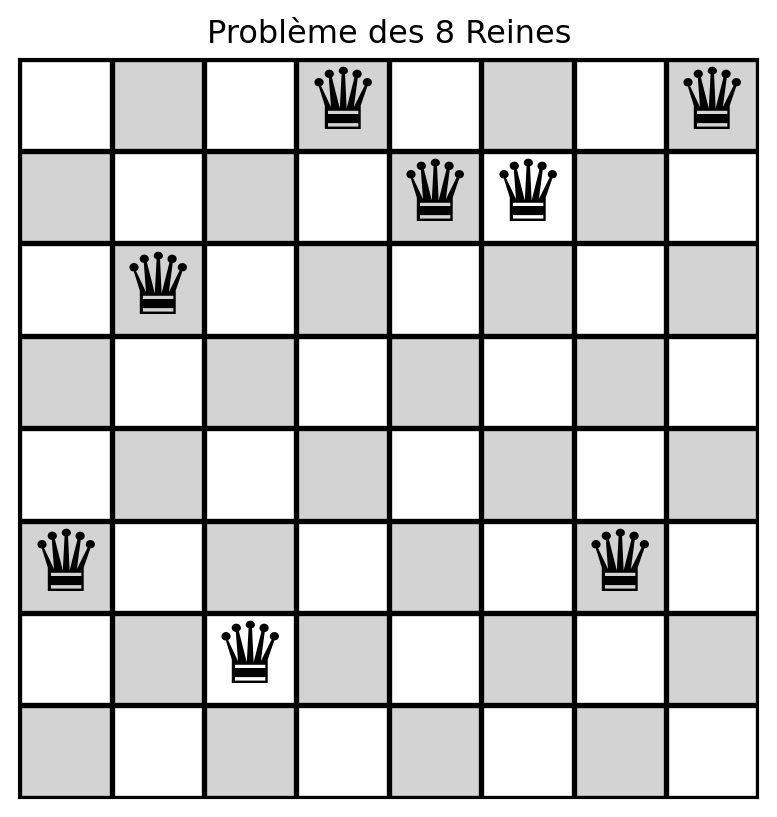
Géron, Aurélien. 2019. Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow. 2nd éd. O’Reilly Media.

———. 2022. Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow. 3ᵉ éd. O’Reilly Media, Inc.

Goodfellow, Ian, Yoshua Bengio, et Aaron Courville. 2016. Deep Learning. Adaptive computation et machine learning. MIT Press. https://dblp.org/rec/books/daglib/0040158.

Krizhevsky, Alex, Ilya Sutskever, et Geoffrey E Hinton. 2012. « ImageNet Classification with Deep Convolutional Neural Networks ». In Advances in Neural Information Processing Systems, édité par F. Pereira, C. J. Burges, L. Bottou, et K. Q. Weinberger. Vol. 25. Curran Associates, Inc. https://proceedings.neurips.cc/paper_files/paper/2012/file/c399862d3b9d6b76c8436e924a68c45b-Paper.pdf.

LeCun, Yann, Yoshua Bengio, et Geoffrey Hinton. 2015. « Deep learning ». Nature 521 (7553): 436‑44. https://doi.org/10.1038/nature14539.

Lecun, Y., L. Bottou, Y. Bengio, et P. Haffner. 1998. « Gradient-based learning applied to document recognition ». Proceedings of the IEEE 86 (11): 2278‑2324. https://doi.org/10.1109/5.726791.

Prince, Simon J. D. 2023. Understanding Deep Learning. The MIT Press. http://udlbook.com.

Russell, Stuart, et Peter Norvig. 2020. Artificial Intelligence: A Modern Approach. 4ᵉ éd. Pearson. http://aima.cs.berkeley.edu/.

Simonyan, Karen, et Andrew Zisserman. 2015. « Very Deep Convolutional Networks for Large-Scale Image Recognition ». In International Conference on Learning Representations.

Marcel Turcotte

Marcel.Turcotte@uOttawa.ca

École de science informatique et de génie électrique (SIGE)

Université d’Ottawa