[7, 4, 2, 5, 1, 0, 3, 6]
[0, 4, 2, 5, 1, 0, 3, 6] -> # of conflicts = 6
[1, 4, 2, 5, 1, 0, 3, 6] -> # of conflicts = 5
[2, 4, 2, 5, 1, 0, 3, 6] -> # of conflicts = 6
[3, 4, 2, 5, 1, 0, 3, 6] -> # of conflicts = 6
[4, 4, 2, 5, 1, 0, 3, 6] -> # of conflicts = 6
[5, 4, 2, 5, 1, 0, 3, 6] -> # of conflicts = 8
[6, 4, 2, 5, 1, 0, 3, 6] -> # of conflicts = 5
[7, 0, 2, 5, 1, 0, 3, 6] -> # of conflicts = 4
[7, 1, 2, 5, 1, 0, 3, 6] -> # of conflicts = 4
[7, 2, 2, 5, 1, 0, 3, 6] -> # of conflicts = 3
[7, 3, 2, 5, 1, 0, 3, 6] -> # of conflicts = 5
[7, 5, 2, 5, 1, 0, 3, 6] -> # of conflicts = 3
[7, 6, 2, 5, 1, 0, 3, 6] -> # of conflicts = 4
[7, 7, 2, 5, 1, 0, 3, 6] -> # of conflicts = 4
[7, 4, 0, 5, 1, 0, 3, 6] -> # of conflicts = 5
[7, 4, 1, 5, 1, 0, 3, 6] -> # of conflicts = 6
[7, 4, 3, 5, 1, 0, 3, 6] -> # of conflicts = 8
[7, 4, 4, 5, 1, 0, 3, 6] -> # of conflicts = 6
[7, 4, 5, 5, 1, 0, 3, 6] -> # of conflicts = 7
[7, 4, 6, 5, 1, 0, 3, 6] -> # of conflicts = 6
[7, 4, 7, 5, 1, 0, 3, 6] -> # of conflicts = 6
[7, 4, 2, 0, 1, 0, 3, 6] -> # of conflicts = 7
[7, 4, 2, 1, 1, 0, 3, 6] -> # of conflicts = 6
[7, 4, 2, 2, 1, 0, 3, 6] -> # of conflicts = 9
[7, 4, 2, 3, 1, 0, 3, 6] -> # of conflicts = 6
[7, 4, 2, 4, 1, 0, 3, 6] -> # of conflicts = 6
[7, 4, 2, 6, 1, 0, 3, 6] -> # of conflicts = 7
[7, 4, 2, 7, 1, 0, 3, 6] -> # of conflicts = 5
[7, 4, 2, 5, 0, 0, 3, 6] -> # of conflicts = 3
[7, 4, 2, 5, 2, 0, 3, 6] -> # of conflicts = 2
[7, 4, 2, 5, 3, 0, 3, 6] -> # of conflicts = 4
[7, 4, 2, 5, 4, 0, 3, 6] -> # of conflicts = 4
[7, 4, 2, 5, 5, 0, 3, 6] -> # of conflicts = 3
[7, 4, 2, 5, 6, 0, 3, 6] -> # of conflicts = 3
[7, 4, 2, 5, 7, 0, 3, 6] -> # of conflicts = 3
[7, 4, 2, 5, 1, 1, 3, 6] -> # of conflicts = 3
[7, 4, 2, 5, 1, 2, 3, 6] -> # of conflicts = 6
[7, 4, 2, 5, 1, 3, 3, 6] -> # of conflicts = 4
[7, 4, 2, 5, 1, 4, 3, 6] -> # of conflicts = 5
[7, 4, 2, 5, 1, 5, 3, 6] -> # of conflicts = 4
[7, 4, 2, 5, 1, 6, 3, 6] -> # of conflicts = 3
[7, 4, 2, 5, 1, 7, 3, 6] -> # of conflicts = 4
[7, 4, 2, 5, 1, 0, 0, 6] -> # of conflicts = 4
[7, 4, 2, 5, 1, 0, 1, 6] -> # of conflicts = 6
[7, 4, 2, 5, 1, 0, 2, 6] -> # of conflicts = 5
[7, 4, 2, 5, 1, 0, 4, 6] -> # of conflicts = 4
[7, 4, 2, 5, 1, 0, 5, 6] -> # of conflicts = 5
[7, 4, 2, 5, 1, 0, 6, 6] -> # of conflicts = 5
[7, 4, 2, 5, 1, 0, 7, 6] -> # of conflicts = 5
[7, 4, 2, 5, 1, 0, 3, 0] -> # of conflicts = 6
[7, 4, 2, 5, 1, 0, 3, 1] -> # of conflicts = 6
[7, 4, 2, 5, 1, 0, 3, 2] -> # of conflicts = 7
[7, 4, 2, 5, 1, 0, 3, 3] -> # of conflicts = 5
[7, 4, 2, 5, 1, 0, 3, 4] -> # of conflicts = 7
[7, 4, 2, 5, 1, 0, 3, 5] -> # of conflicts = 5
[7, 4, 2, 5, 1, 0, 3, 7] -> # of conflicts = 6

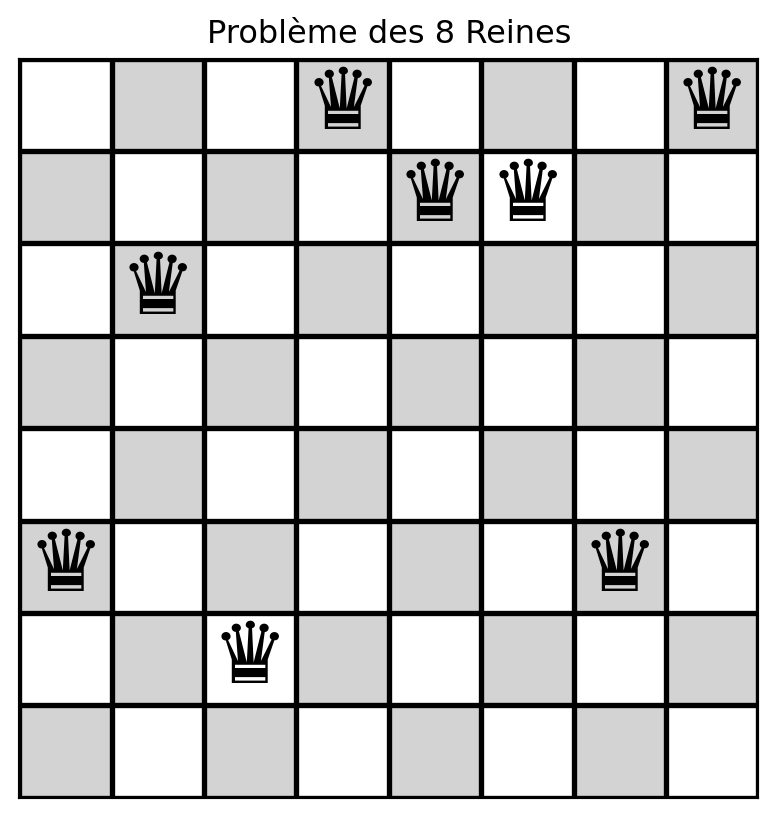
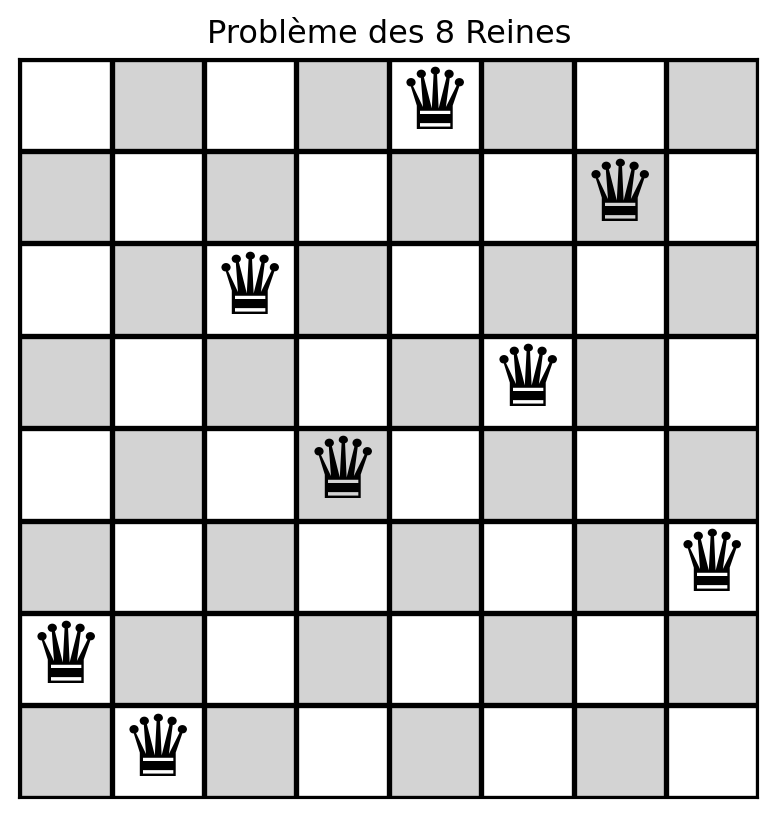
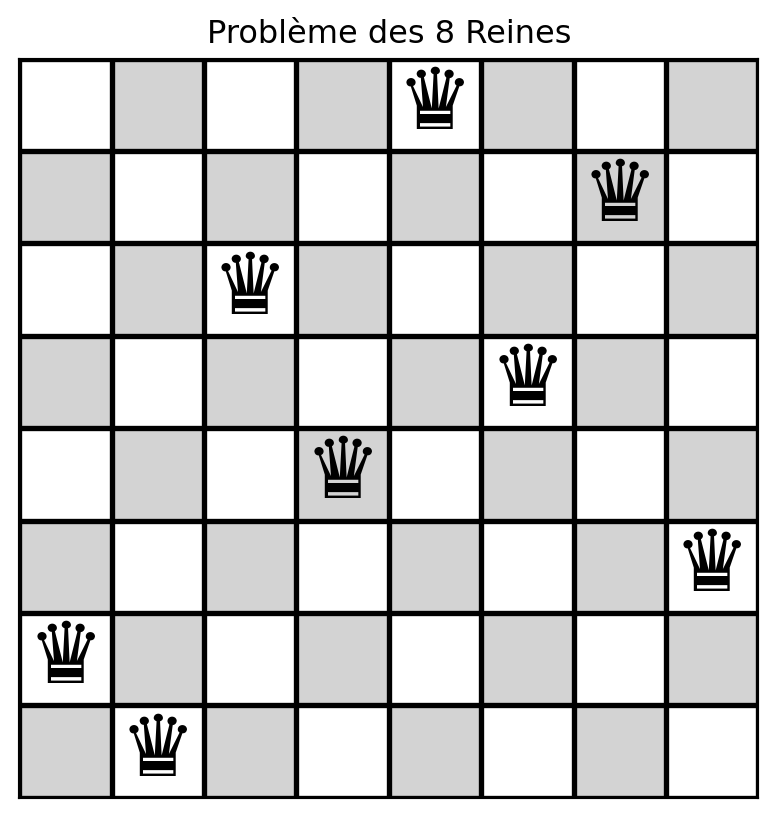


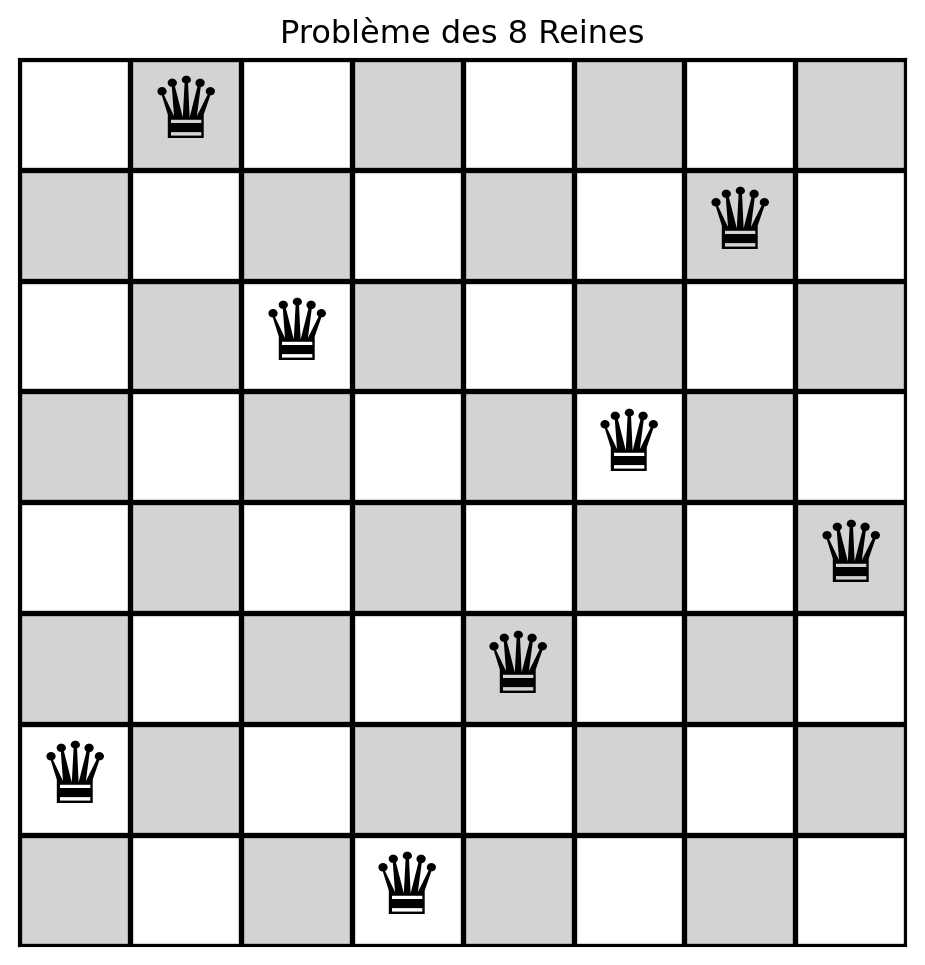
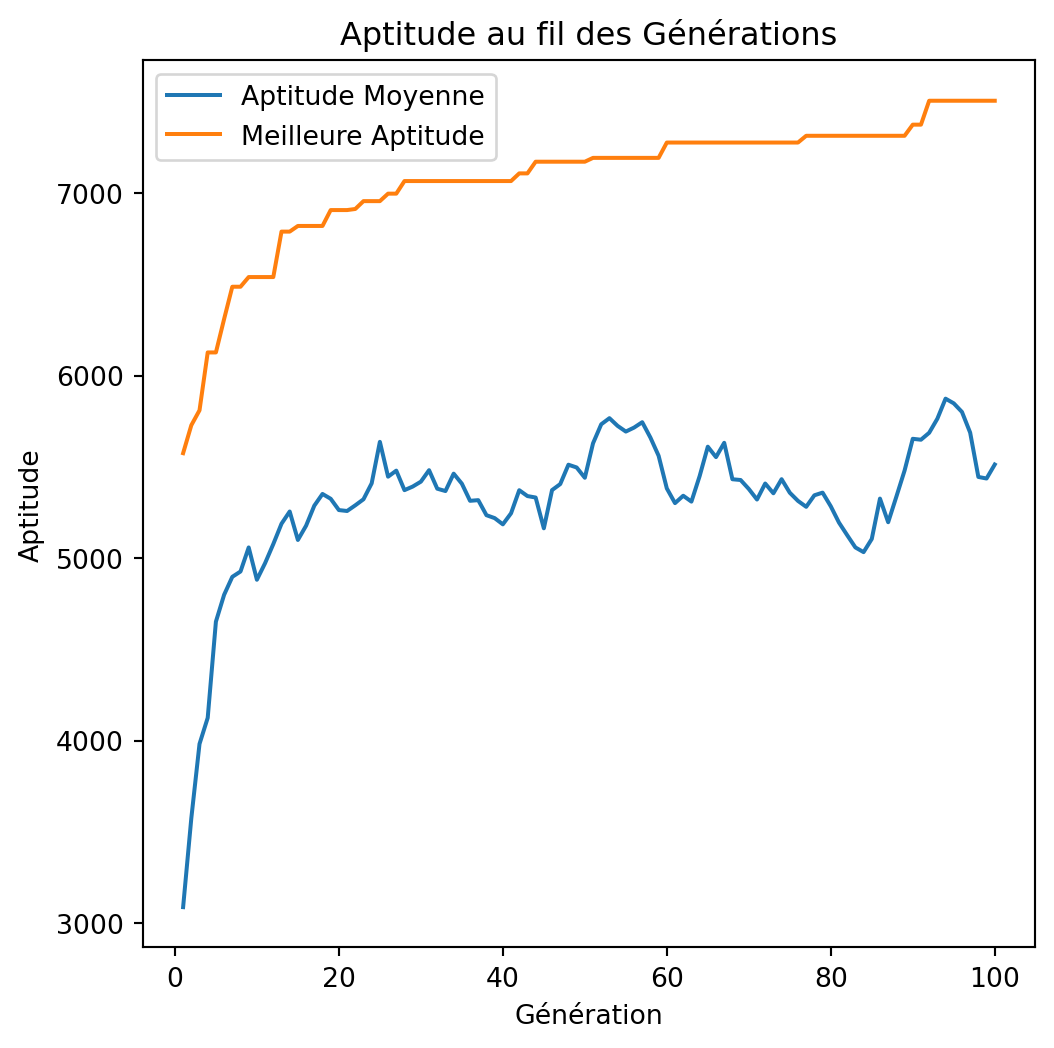




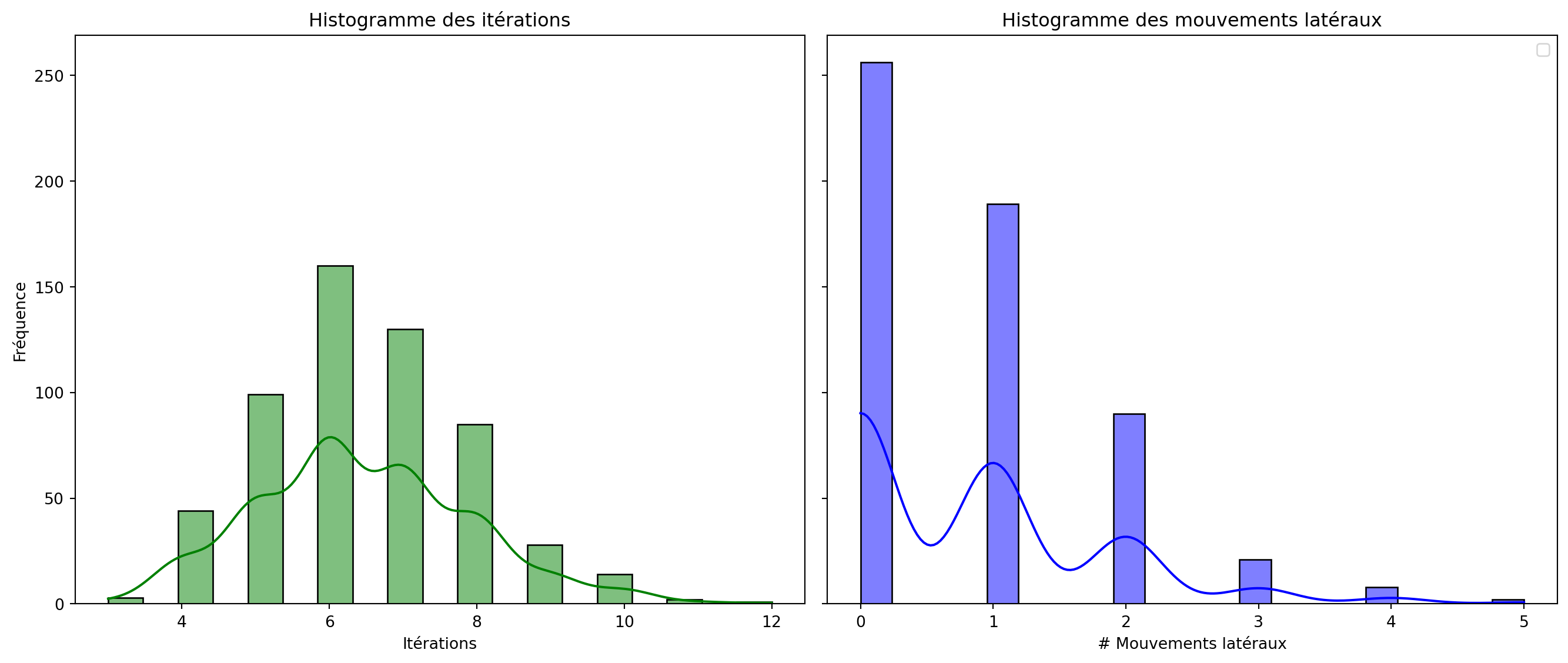
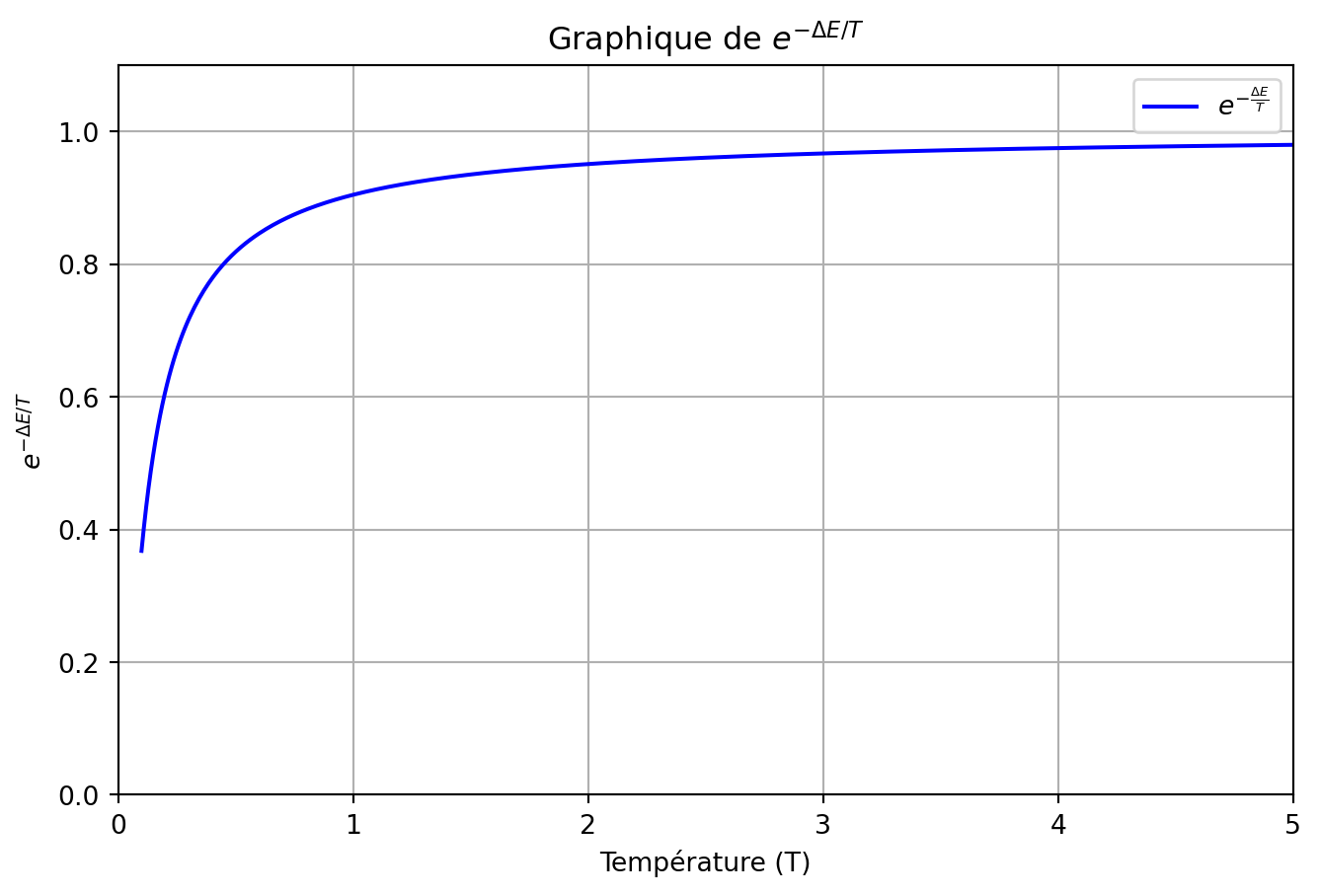

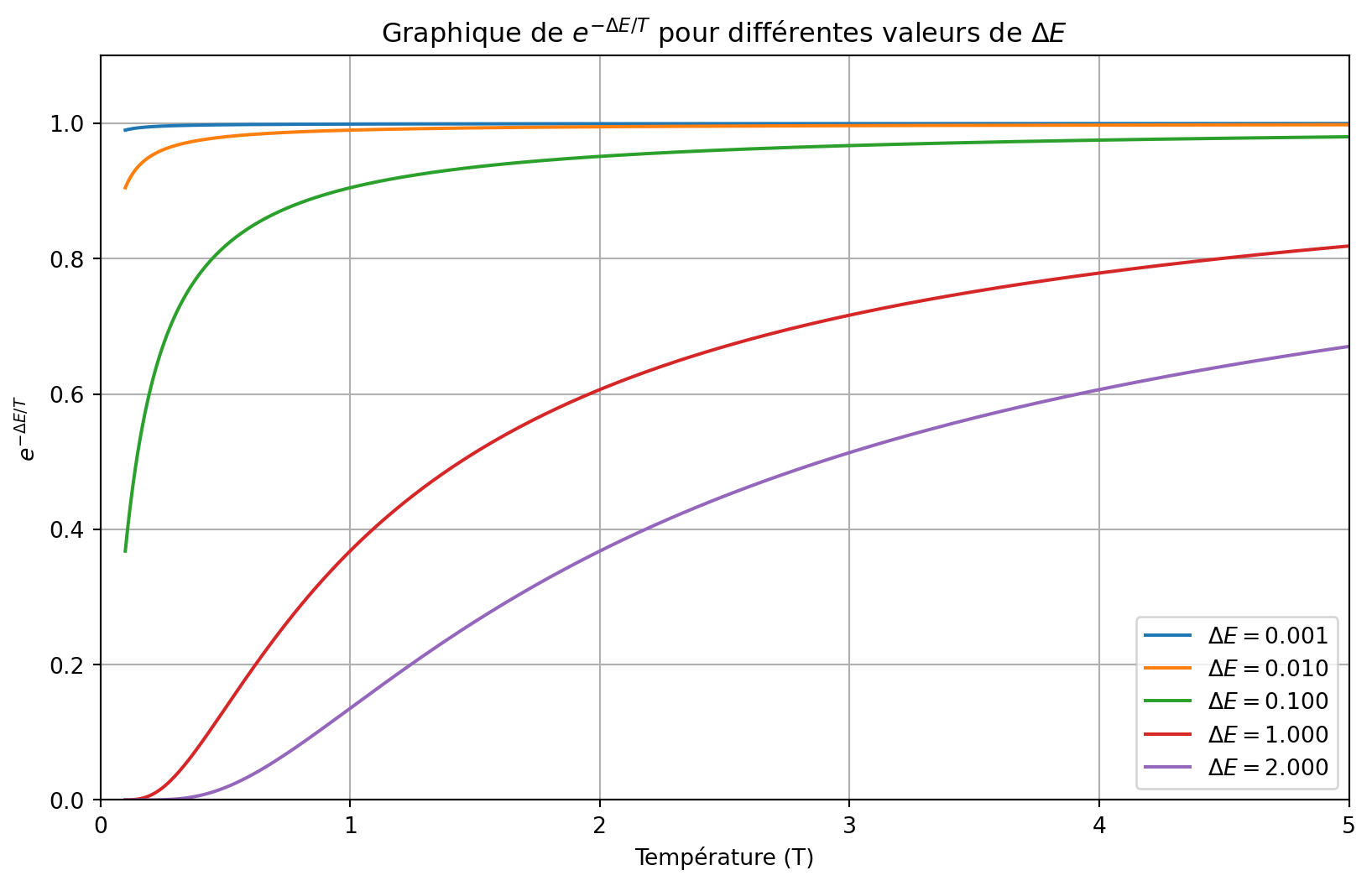
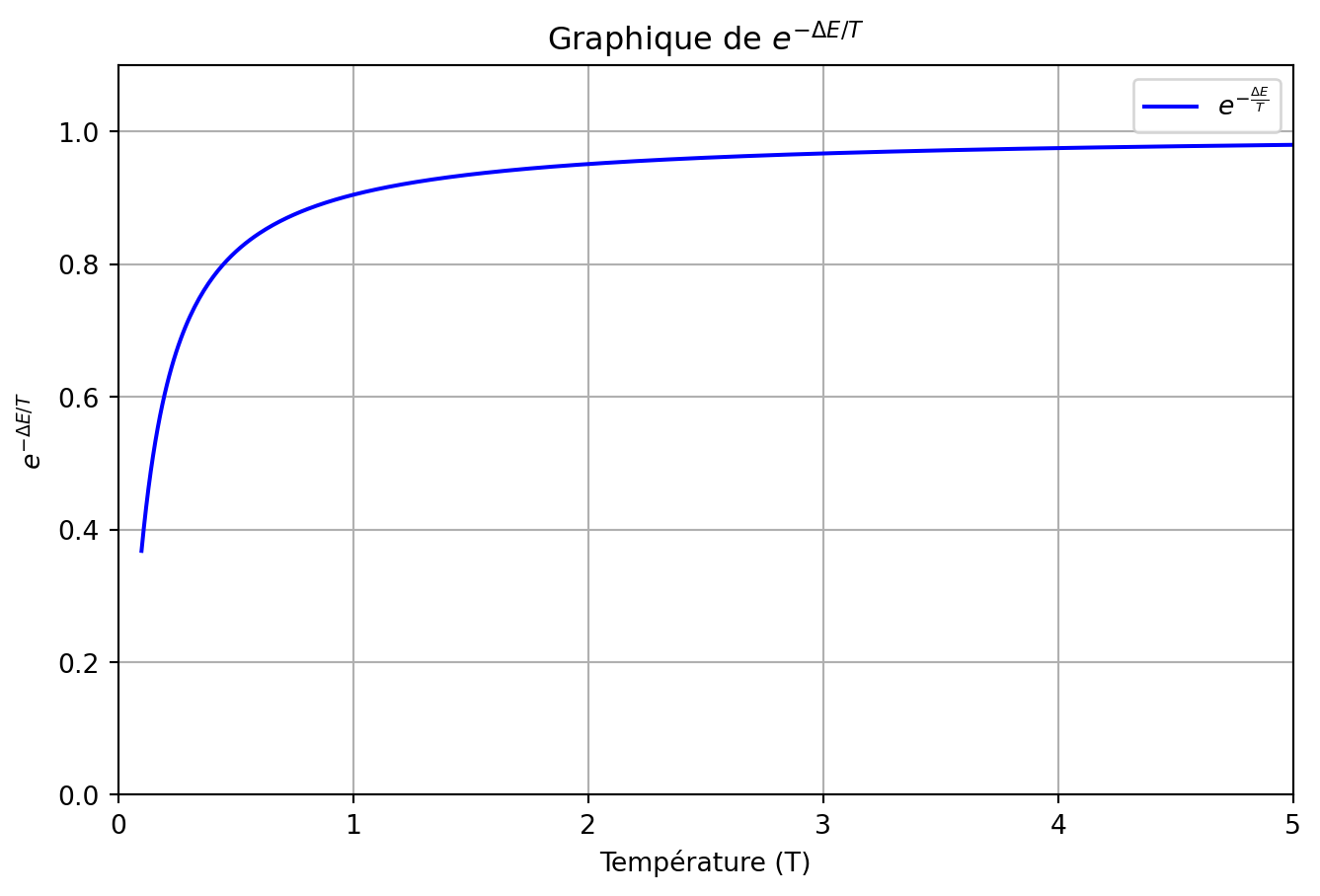
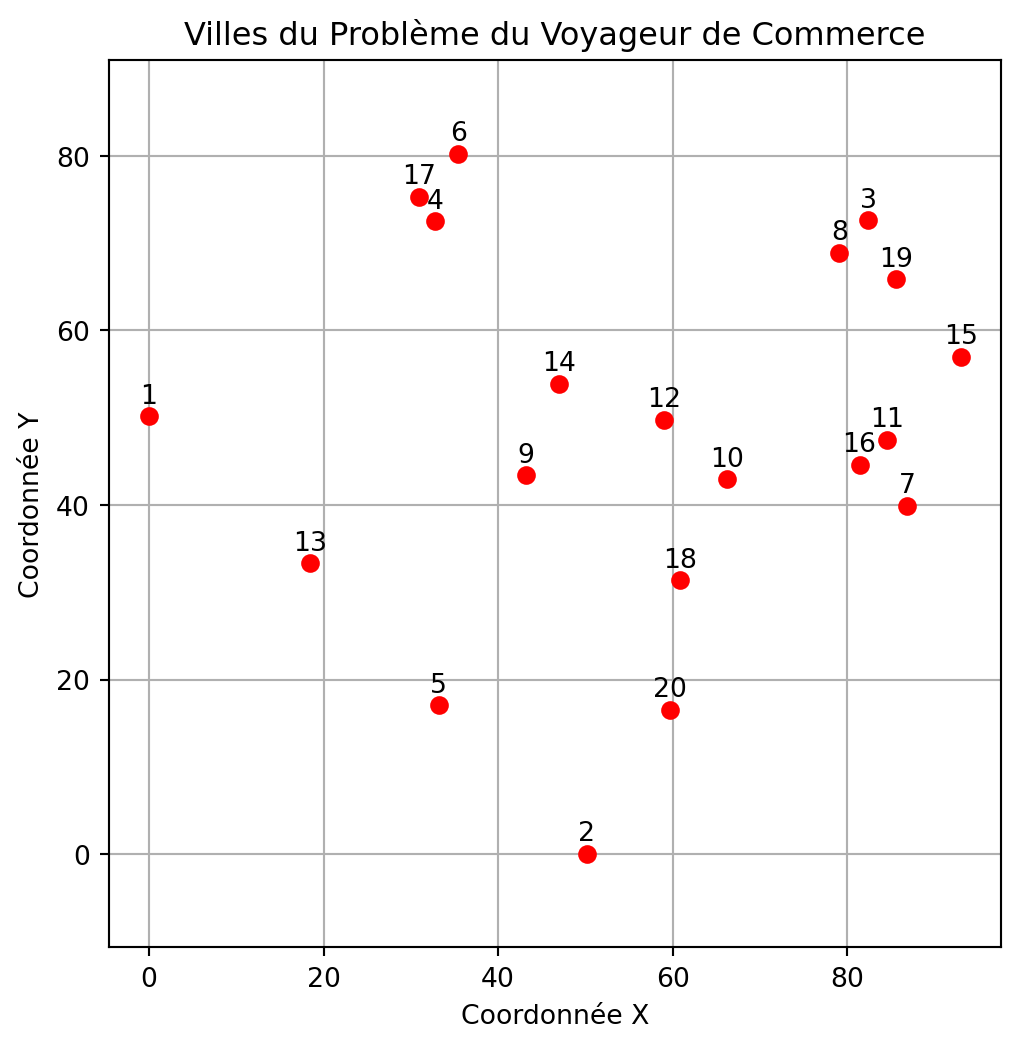
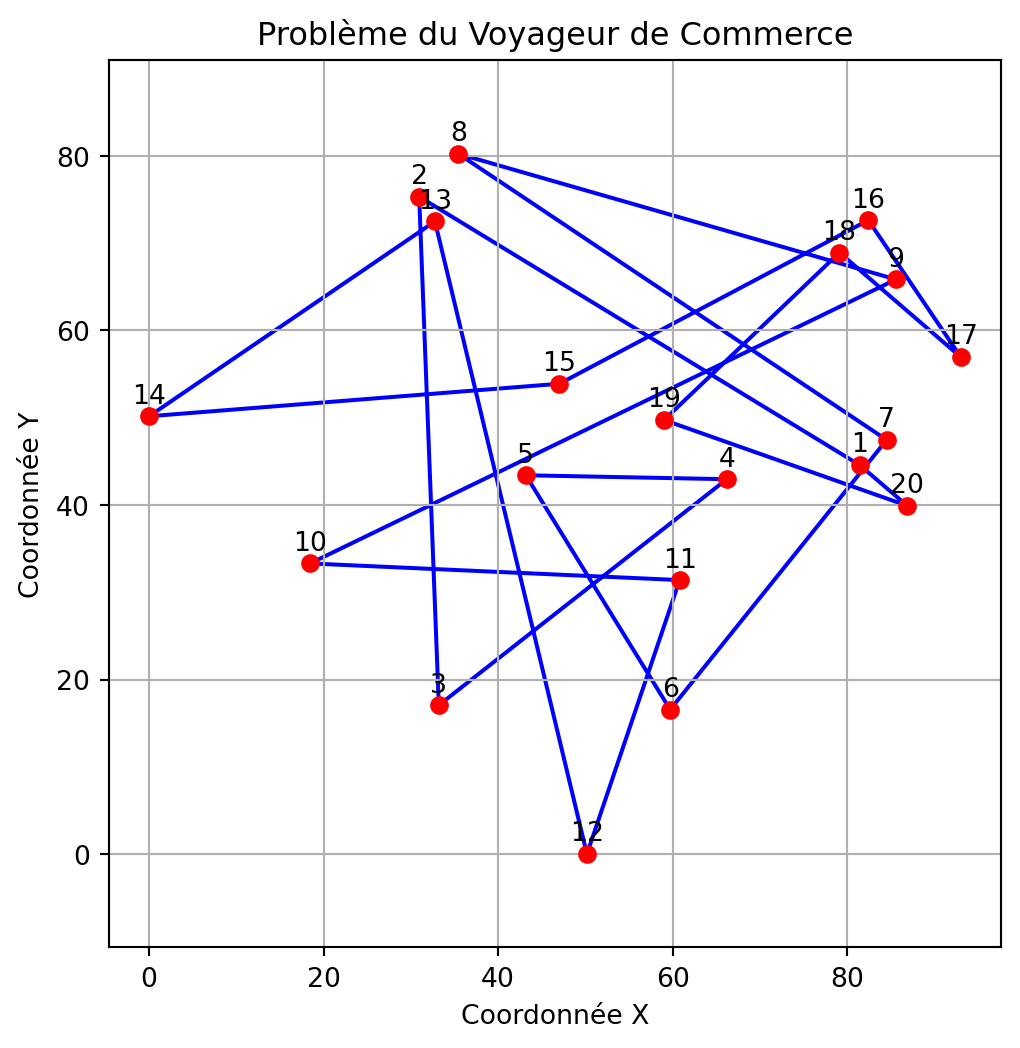
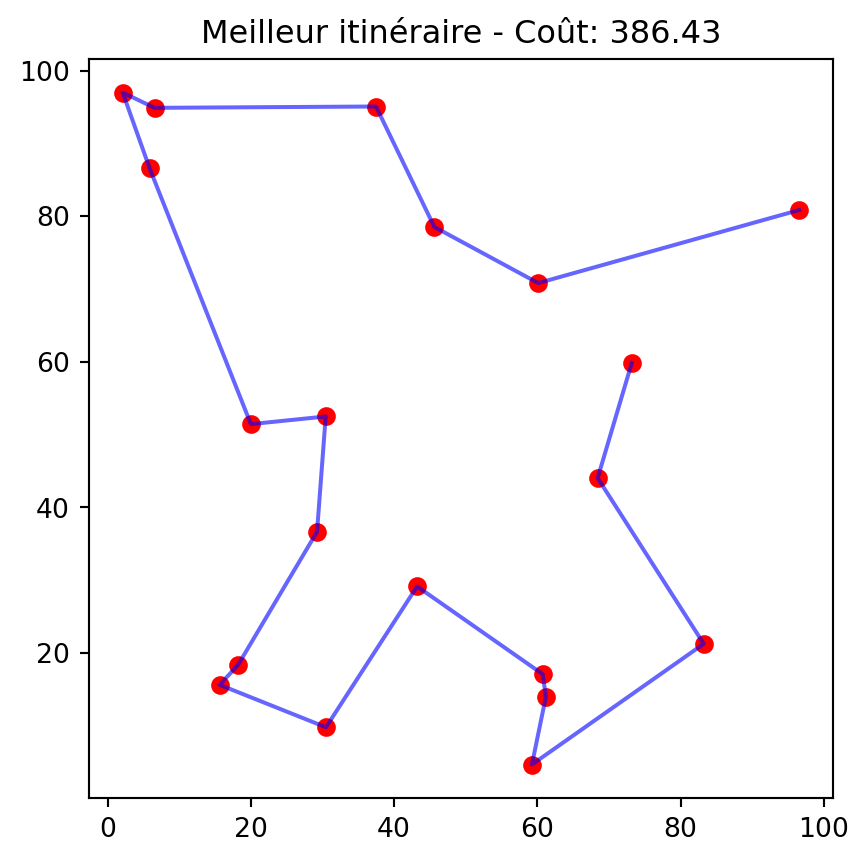
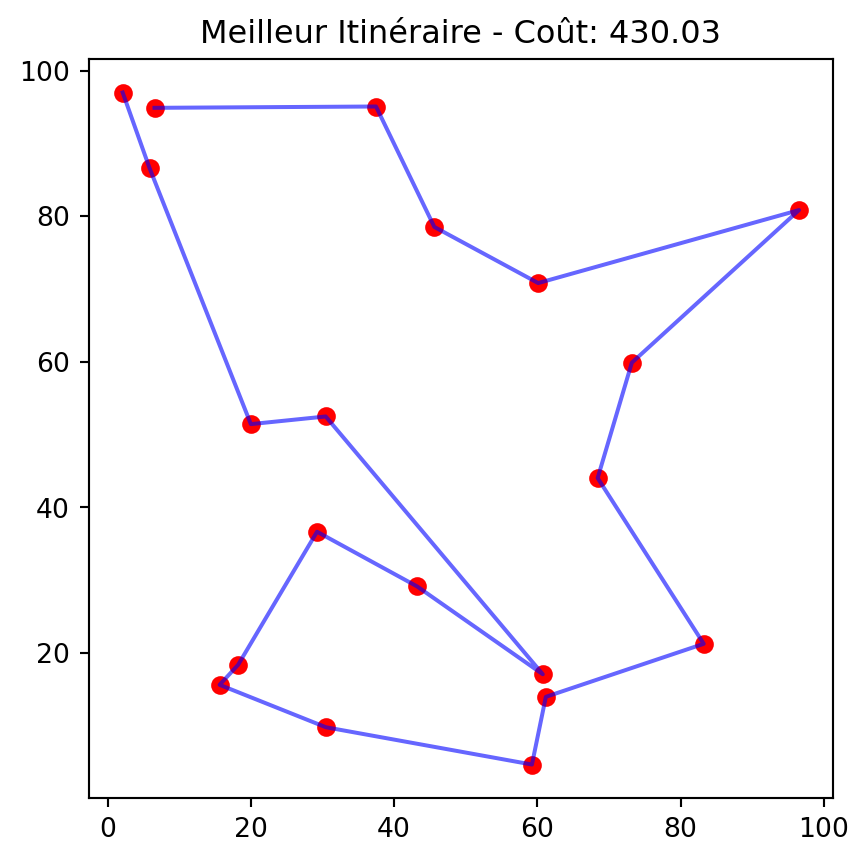
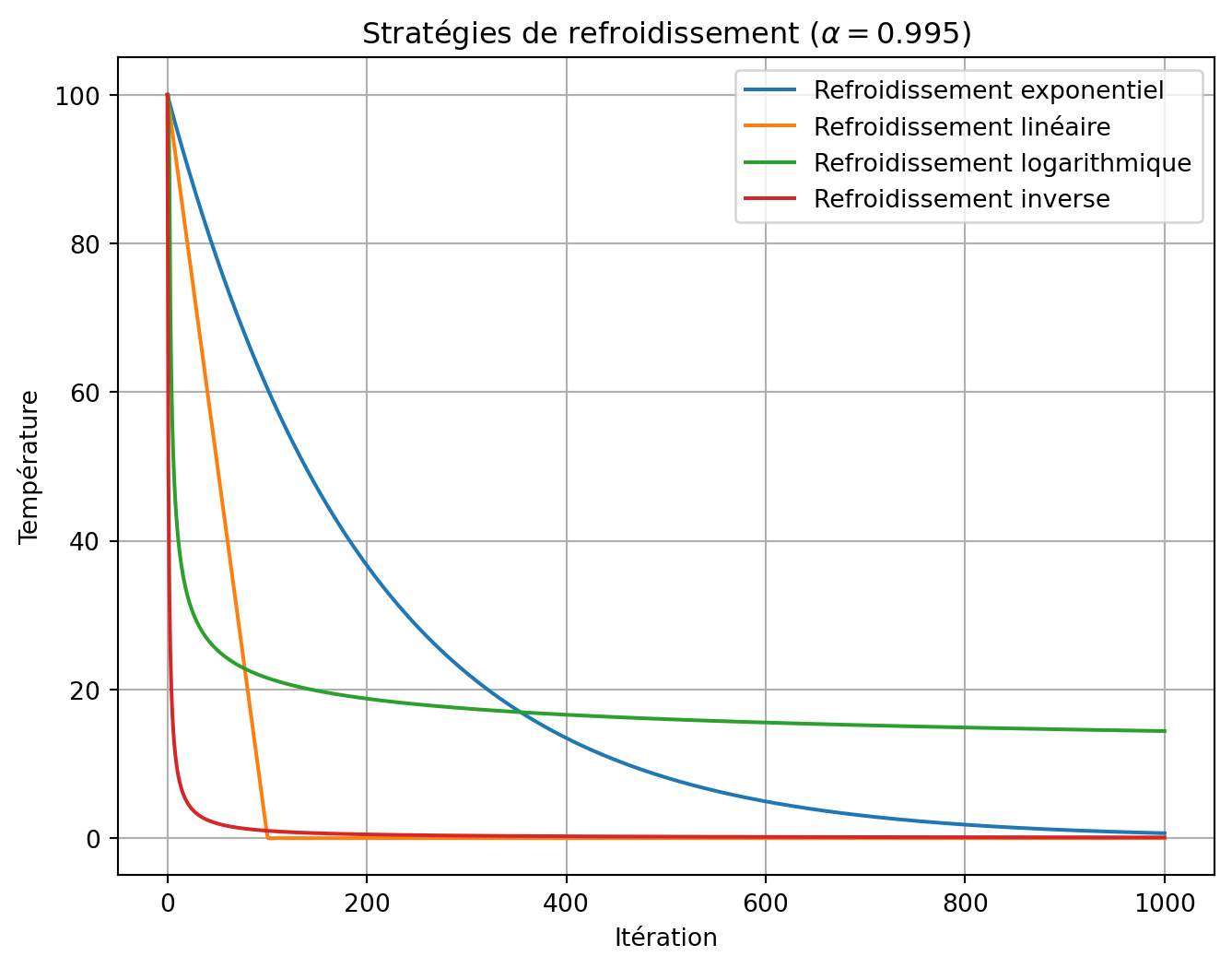
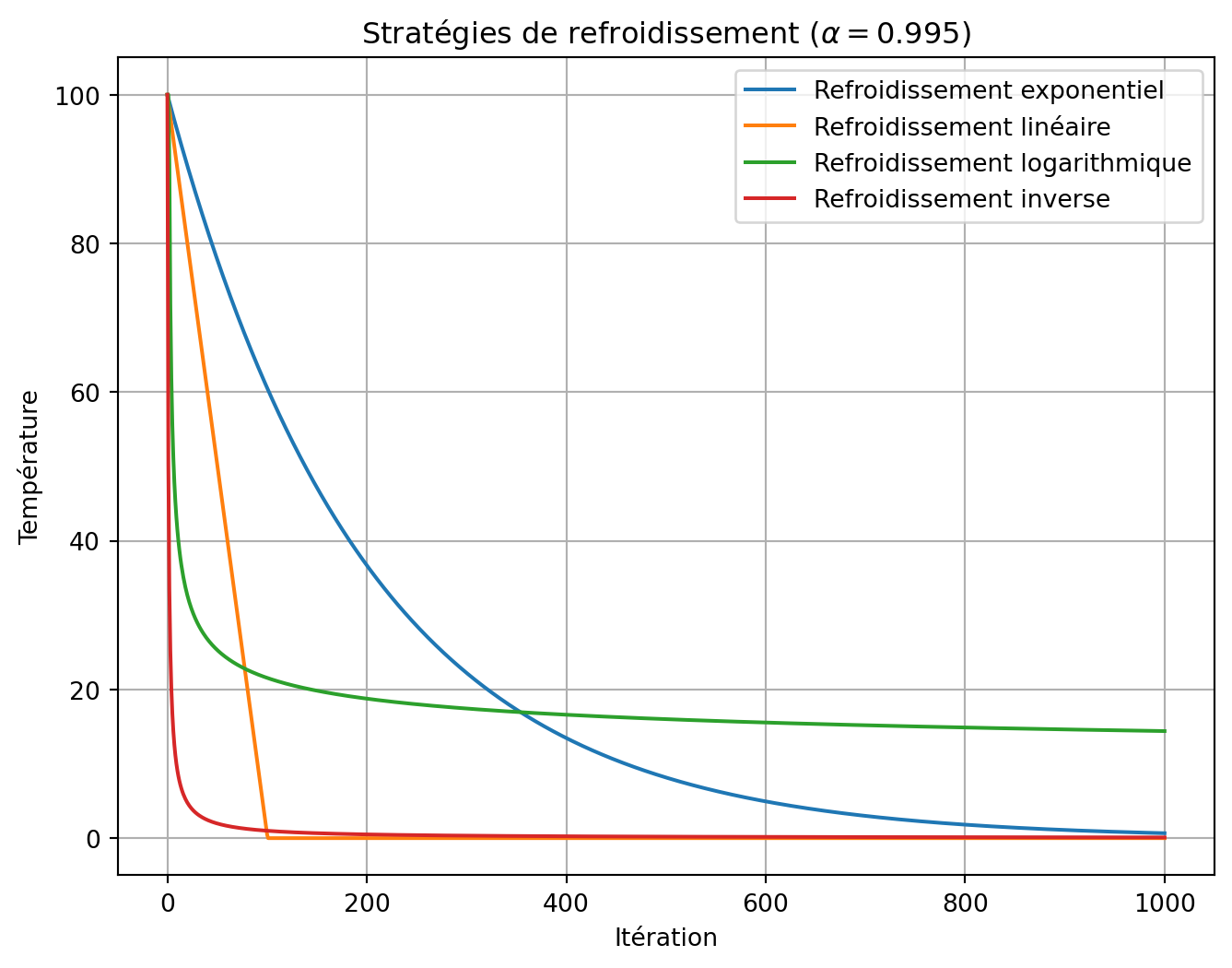

Comment représenter une solution?
Nous utiliserons une liste dans laquelle chaque élément représente l’indice d’une ville, et l’ordre des éléments indique la séquence de visite des villes.