class MinimaxAlphaBetaSolverV2(Solver):
"""
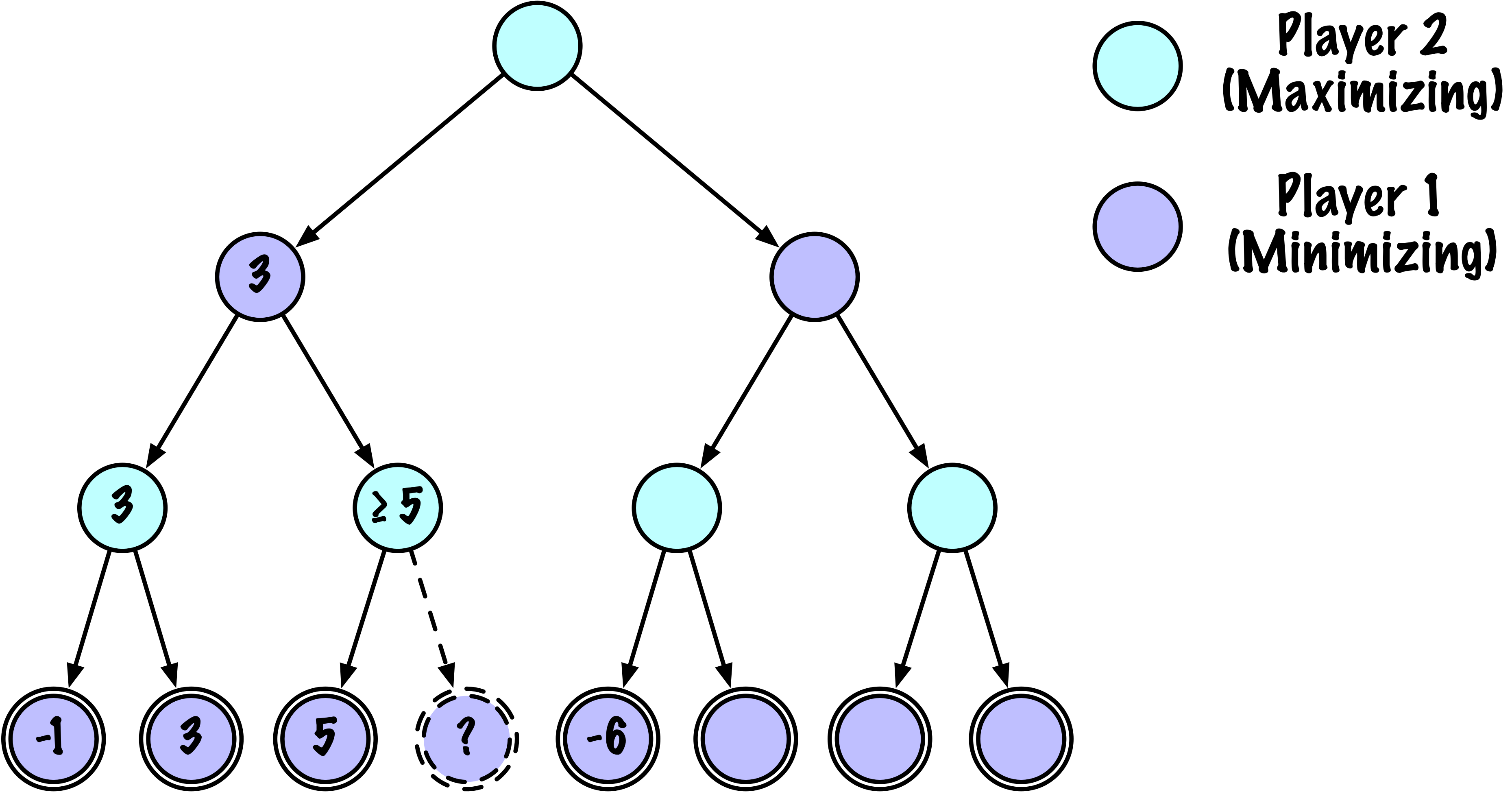
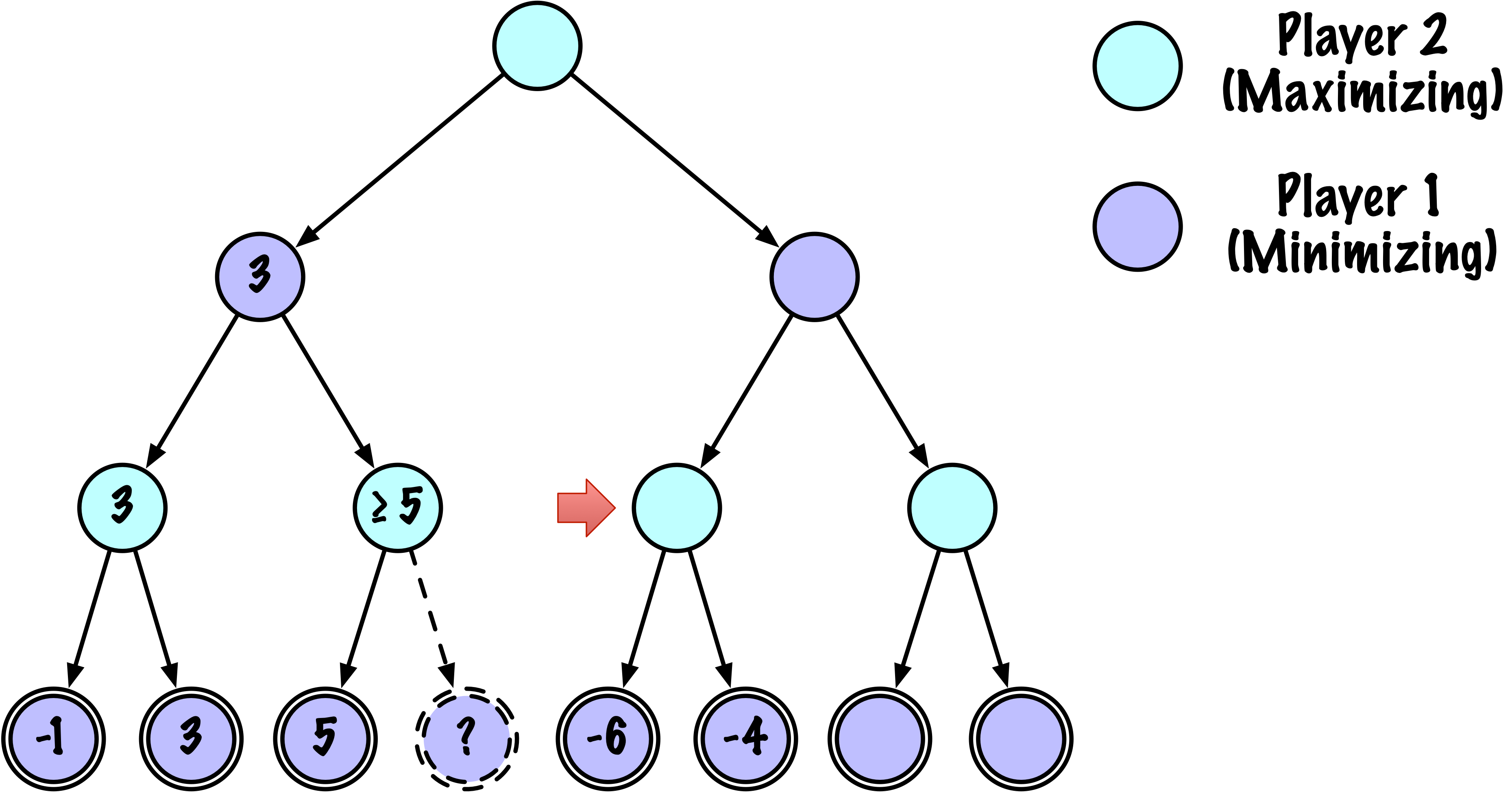
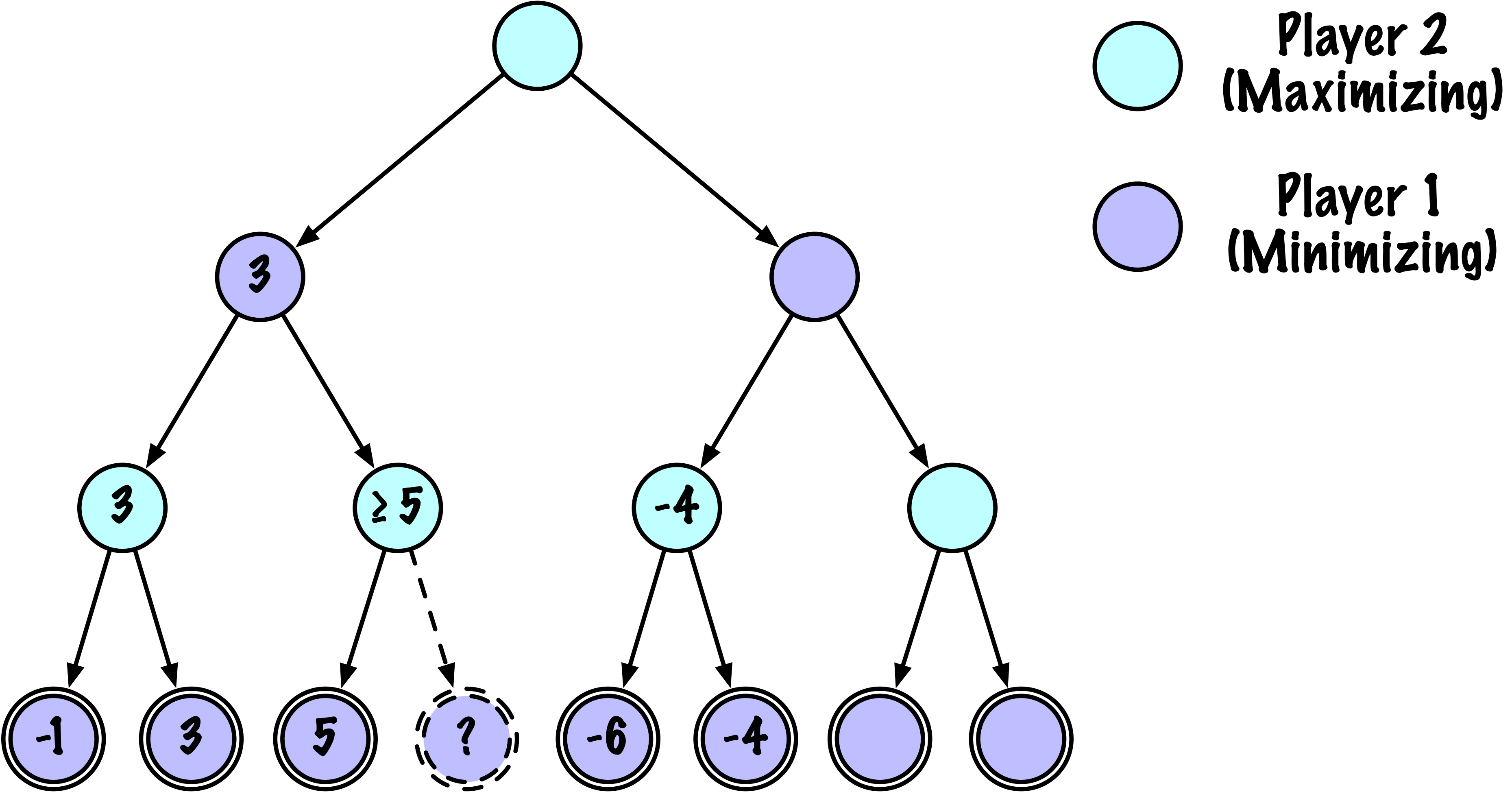
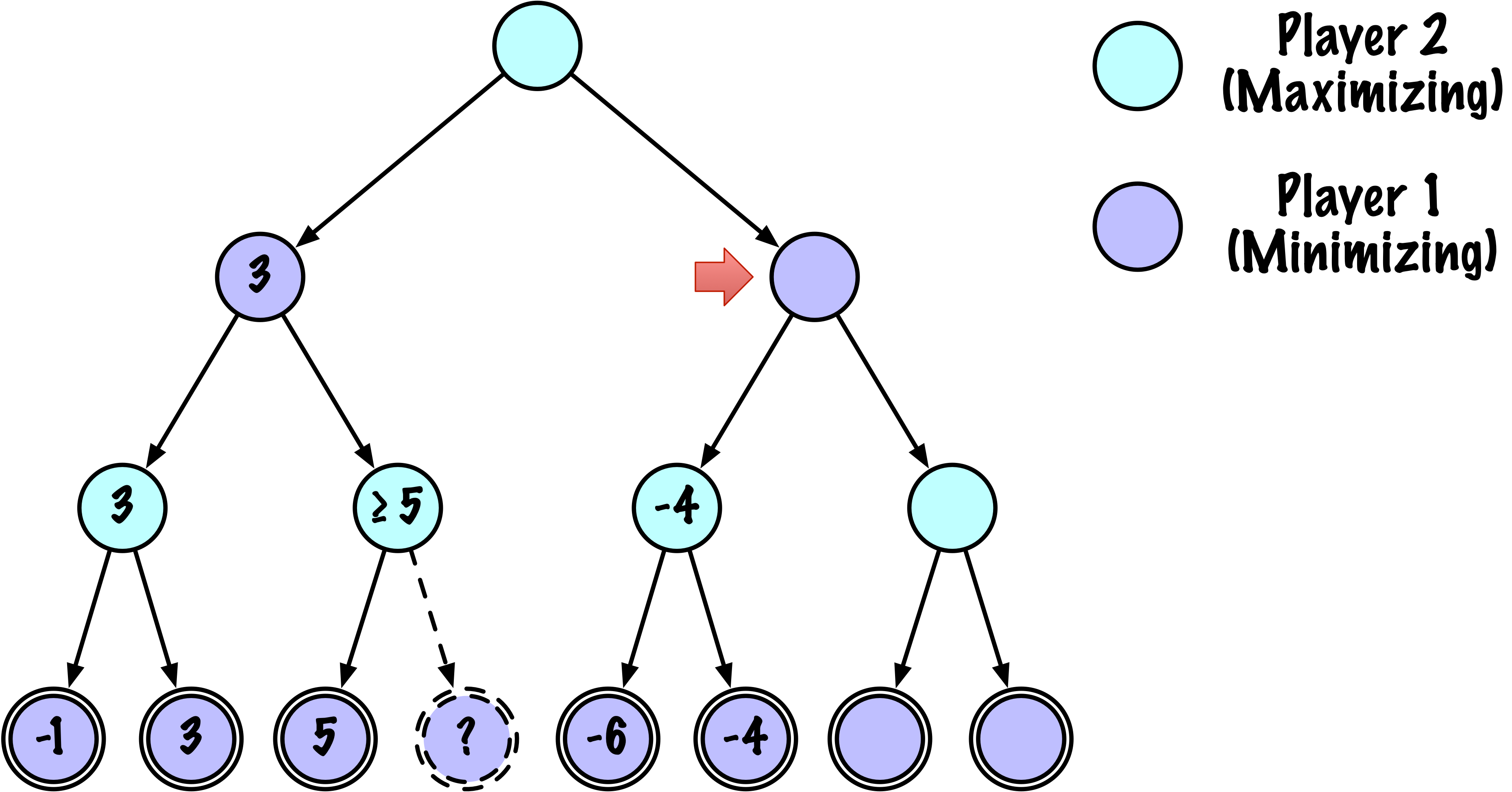
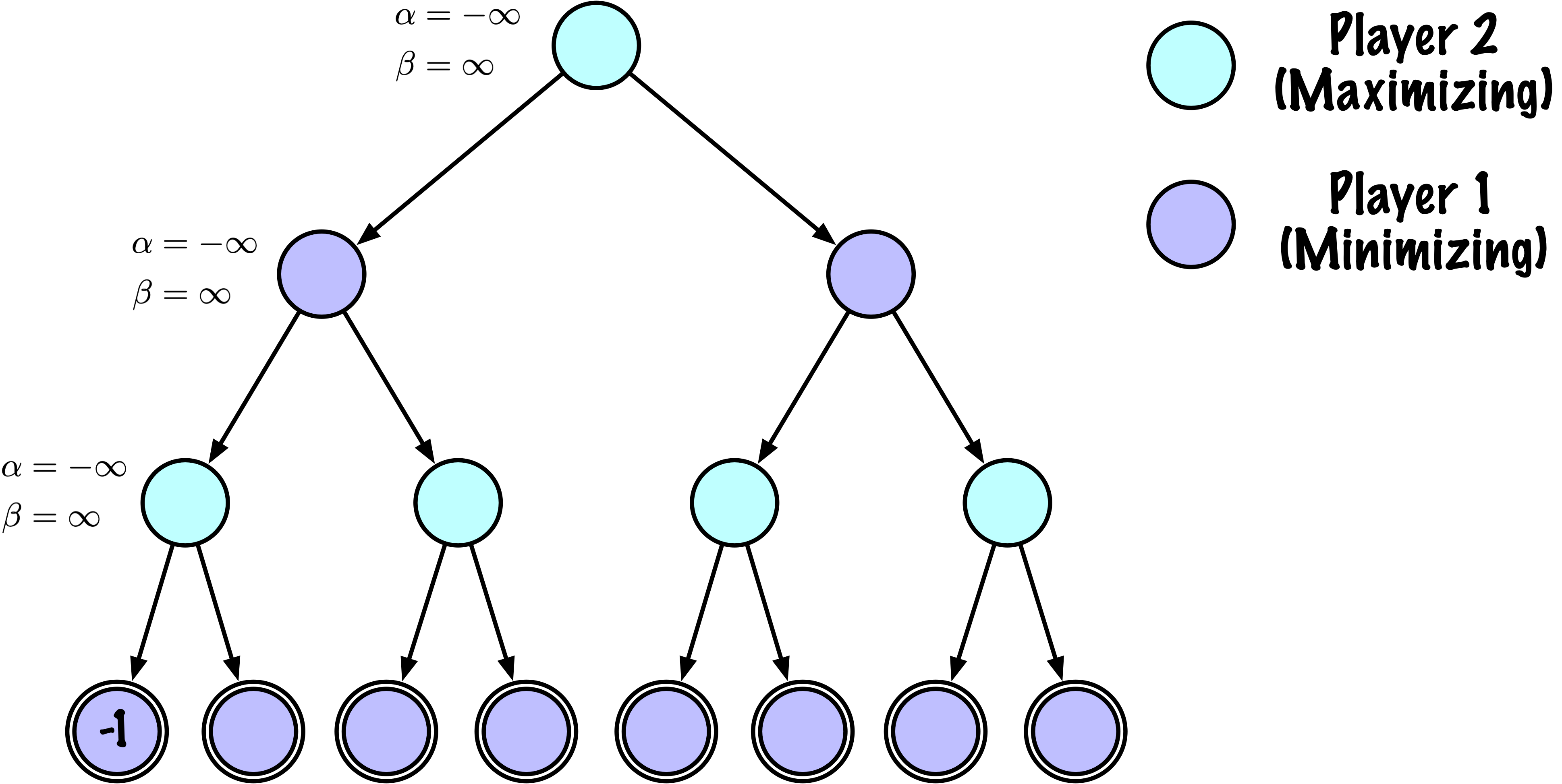
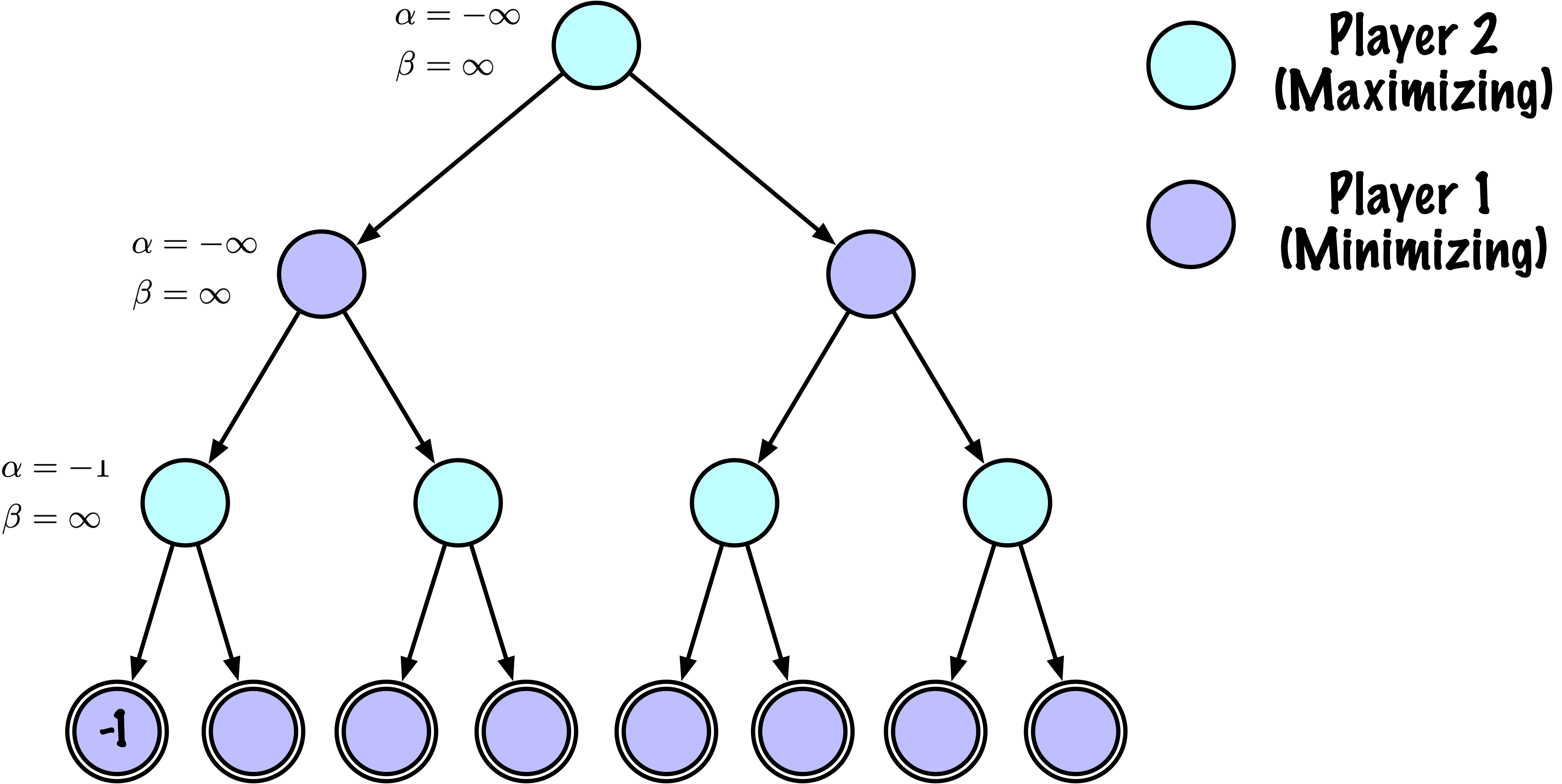
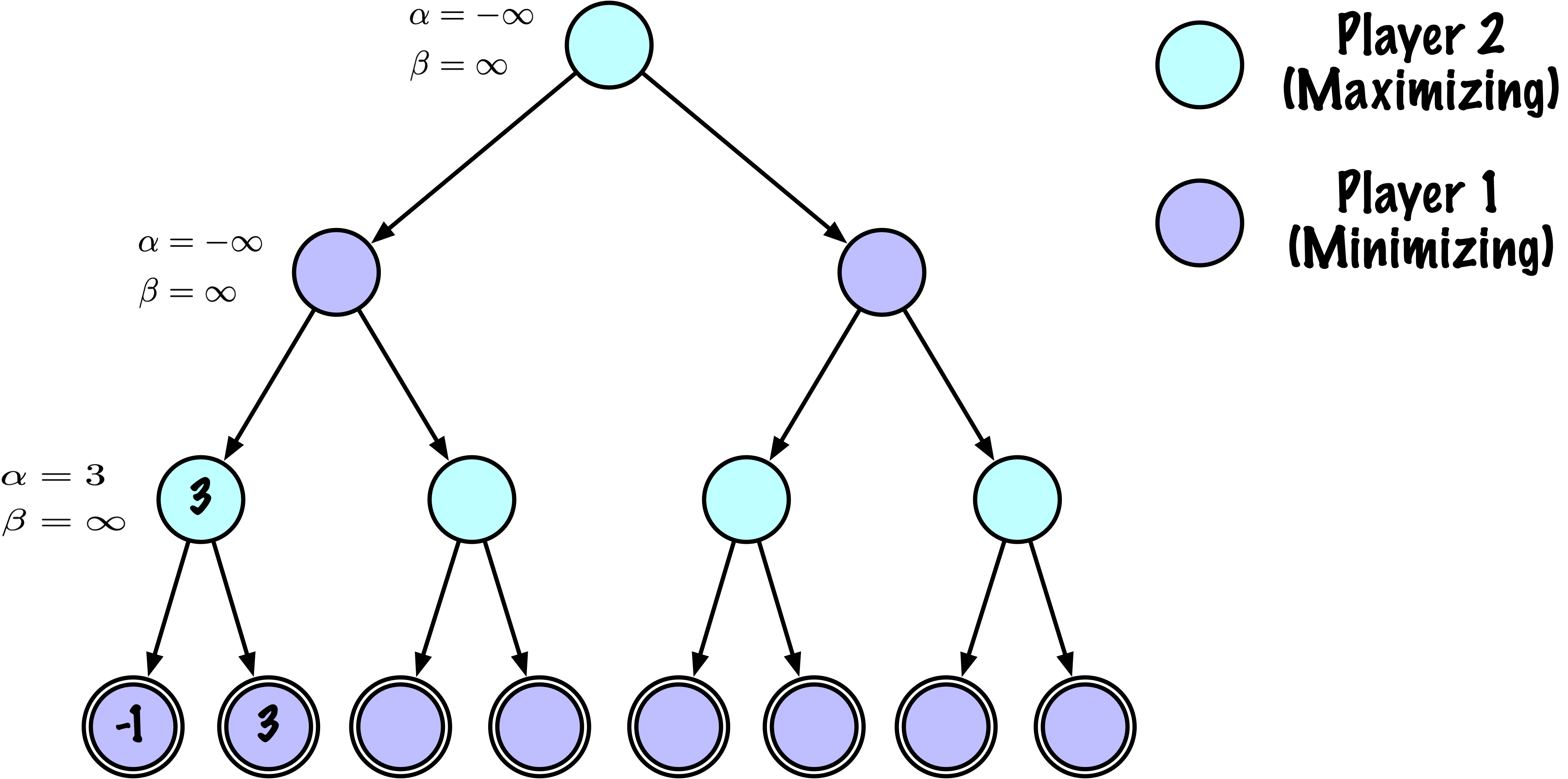
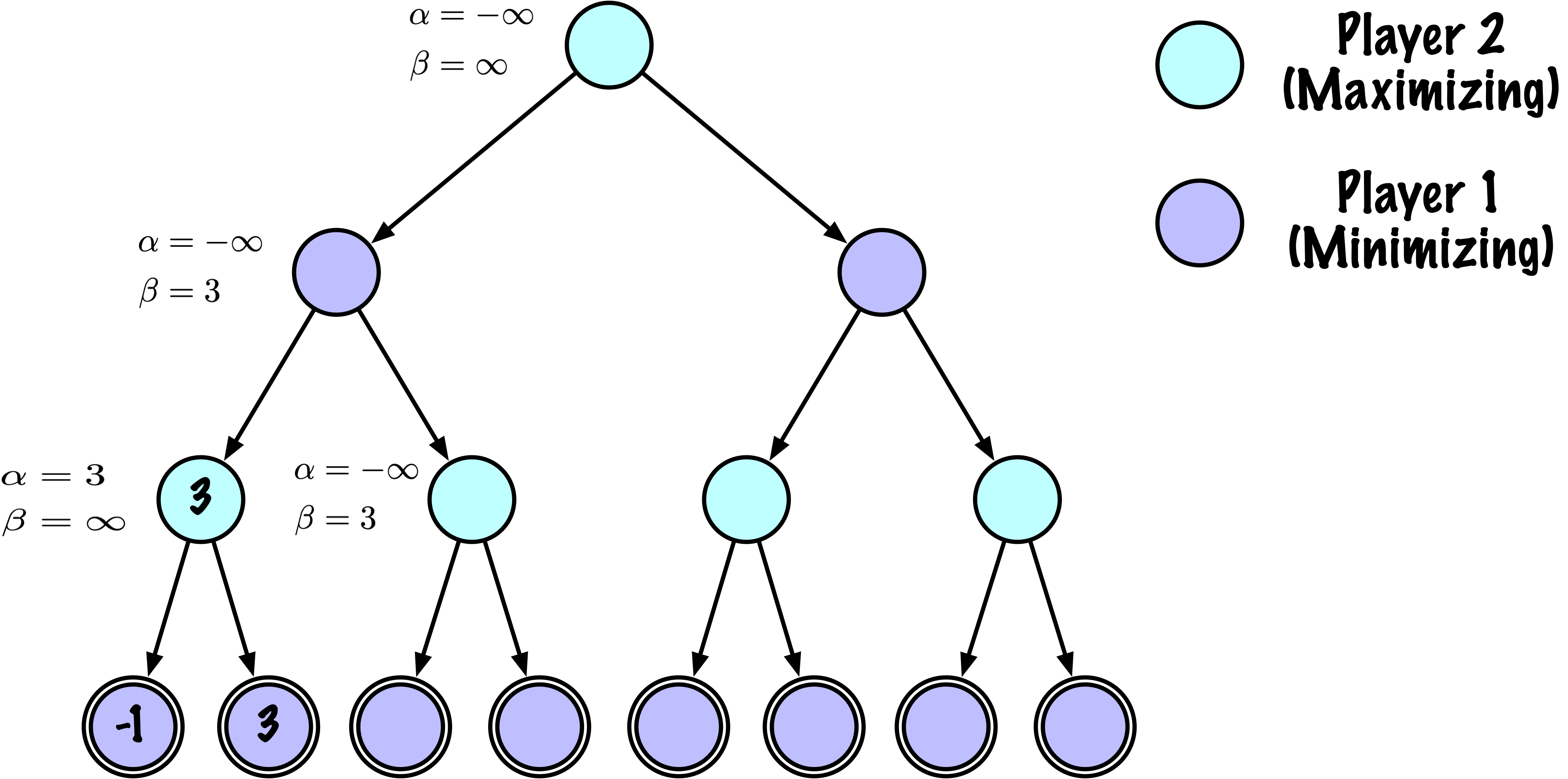
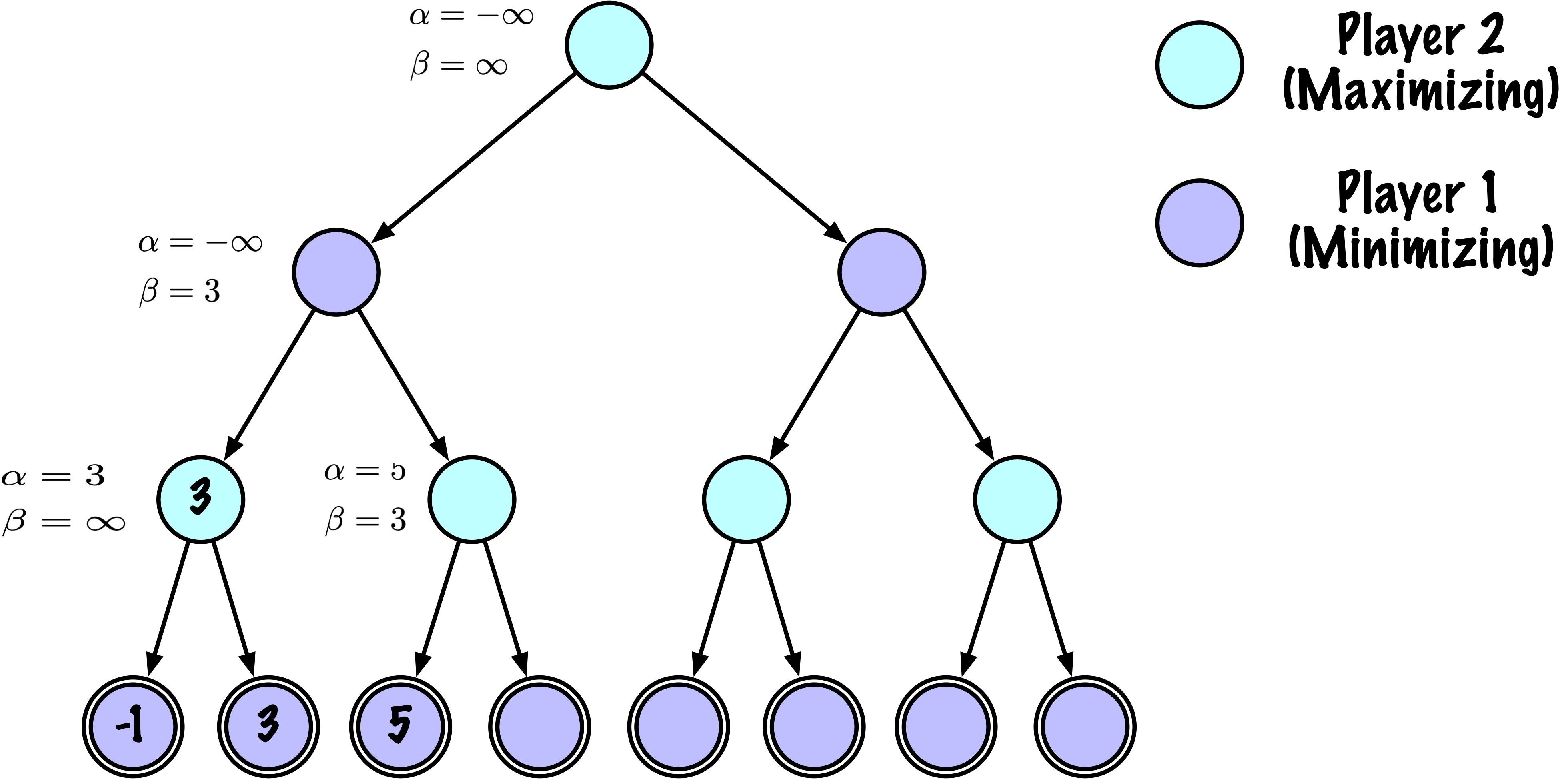
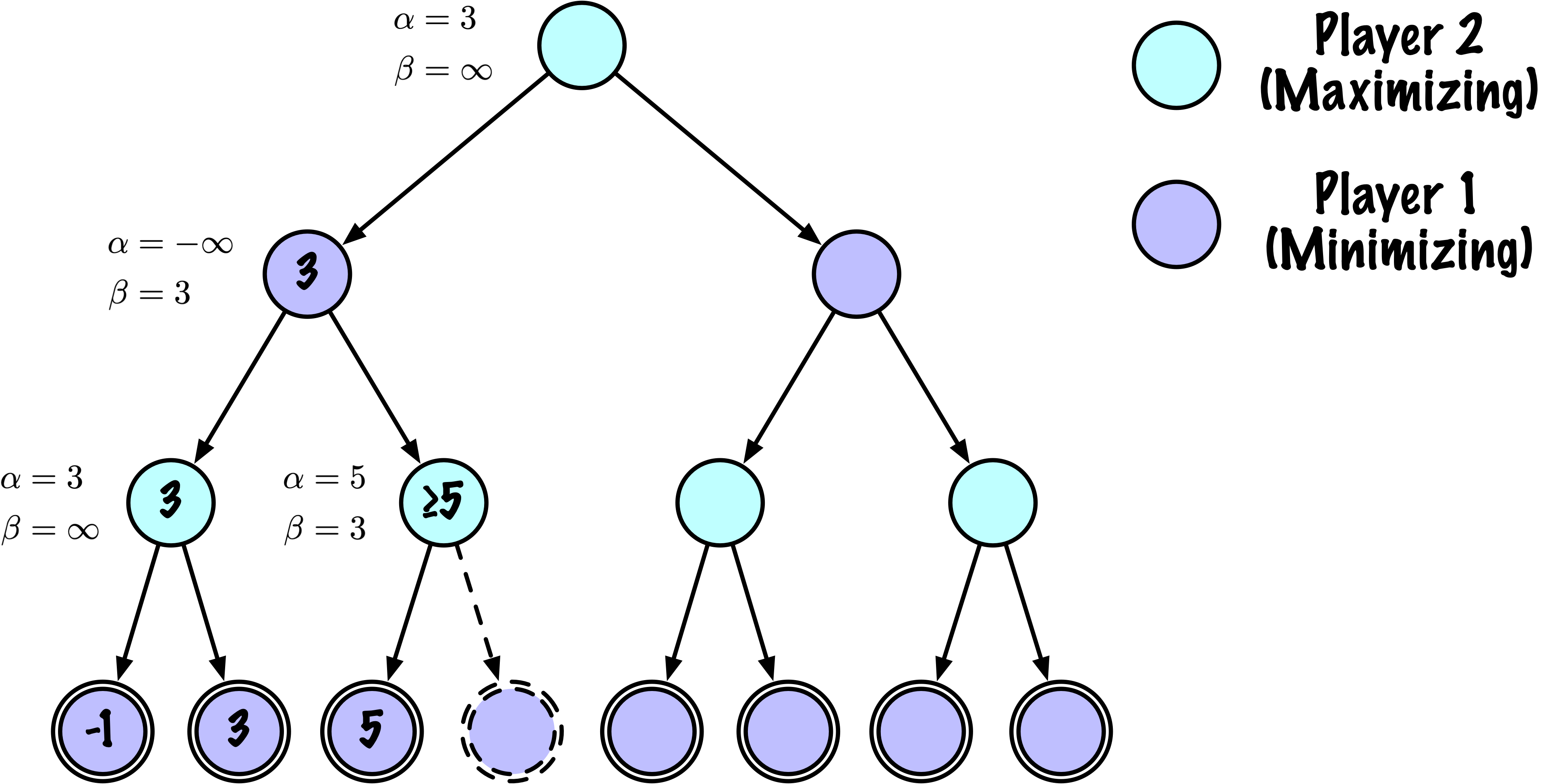
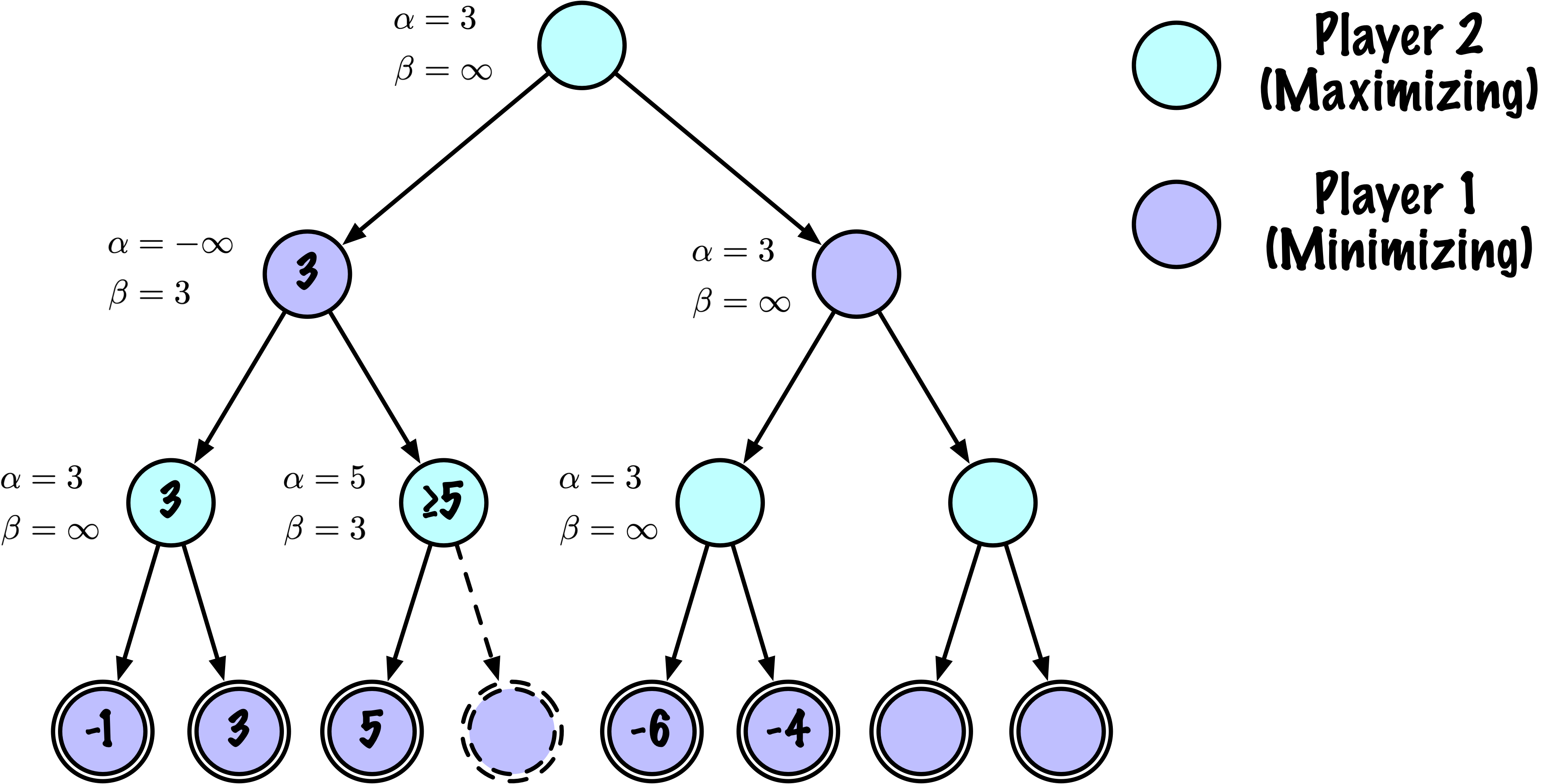
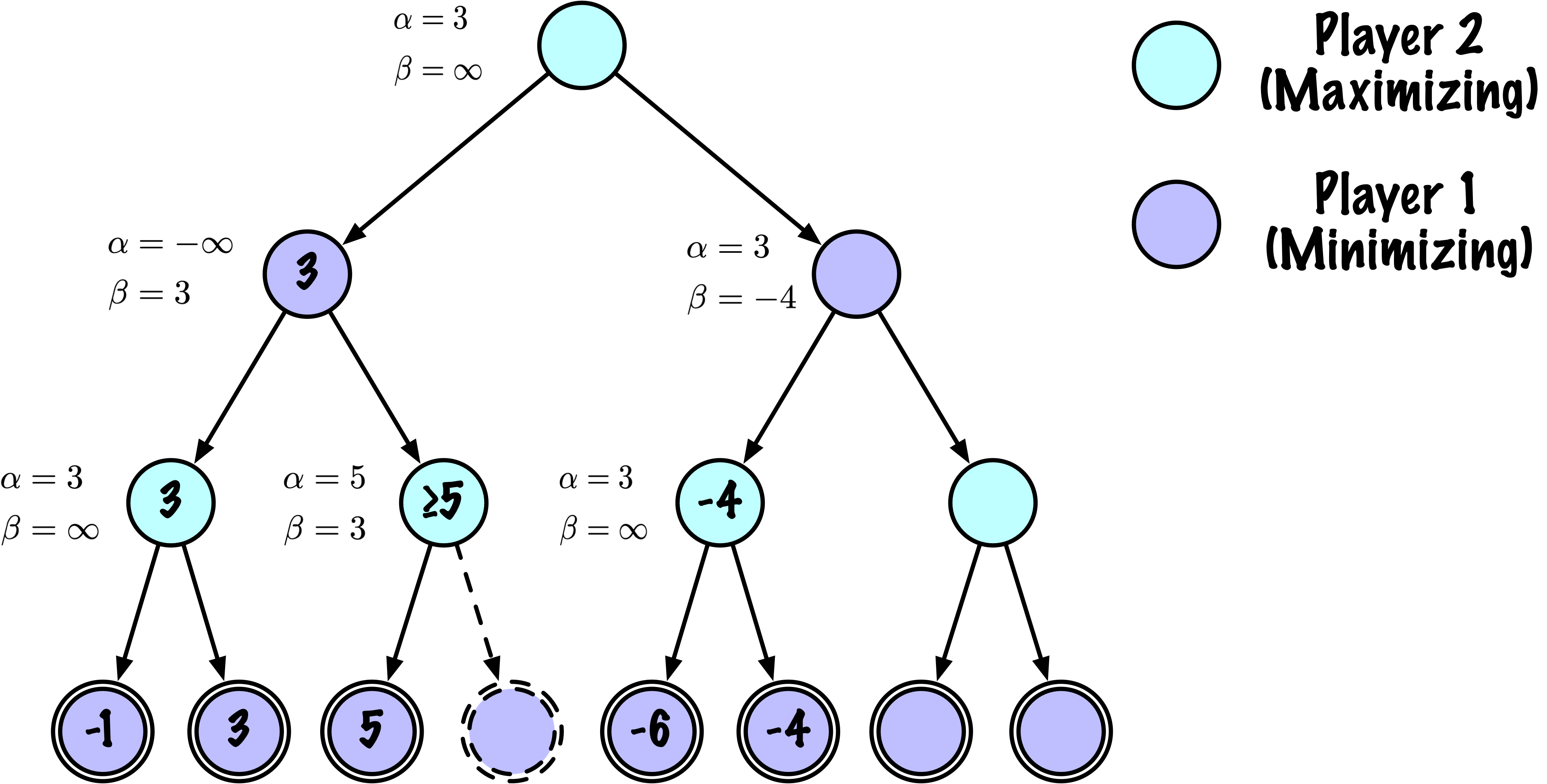
Un solveur Minimax classique amélioré avec l'élagage Alpha–Bêta,
instrumenté pour compter le nombre de nœuds visités.
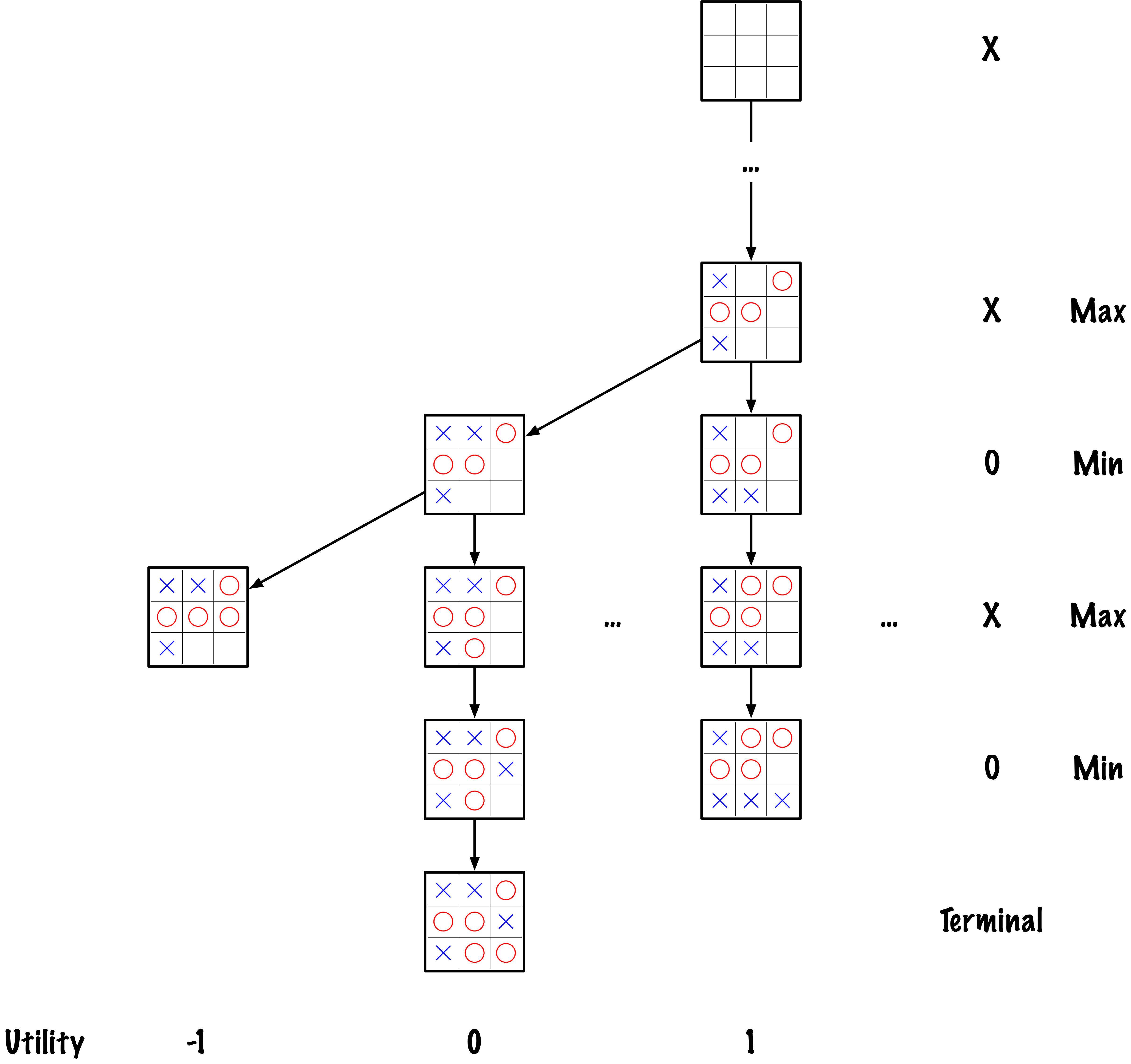
- Suppose que "X" est le joueur maximisant.
- Effectue une exploration complète de l'arbre du jeu de Tic–Tac–Toe.
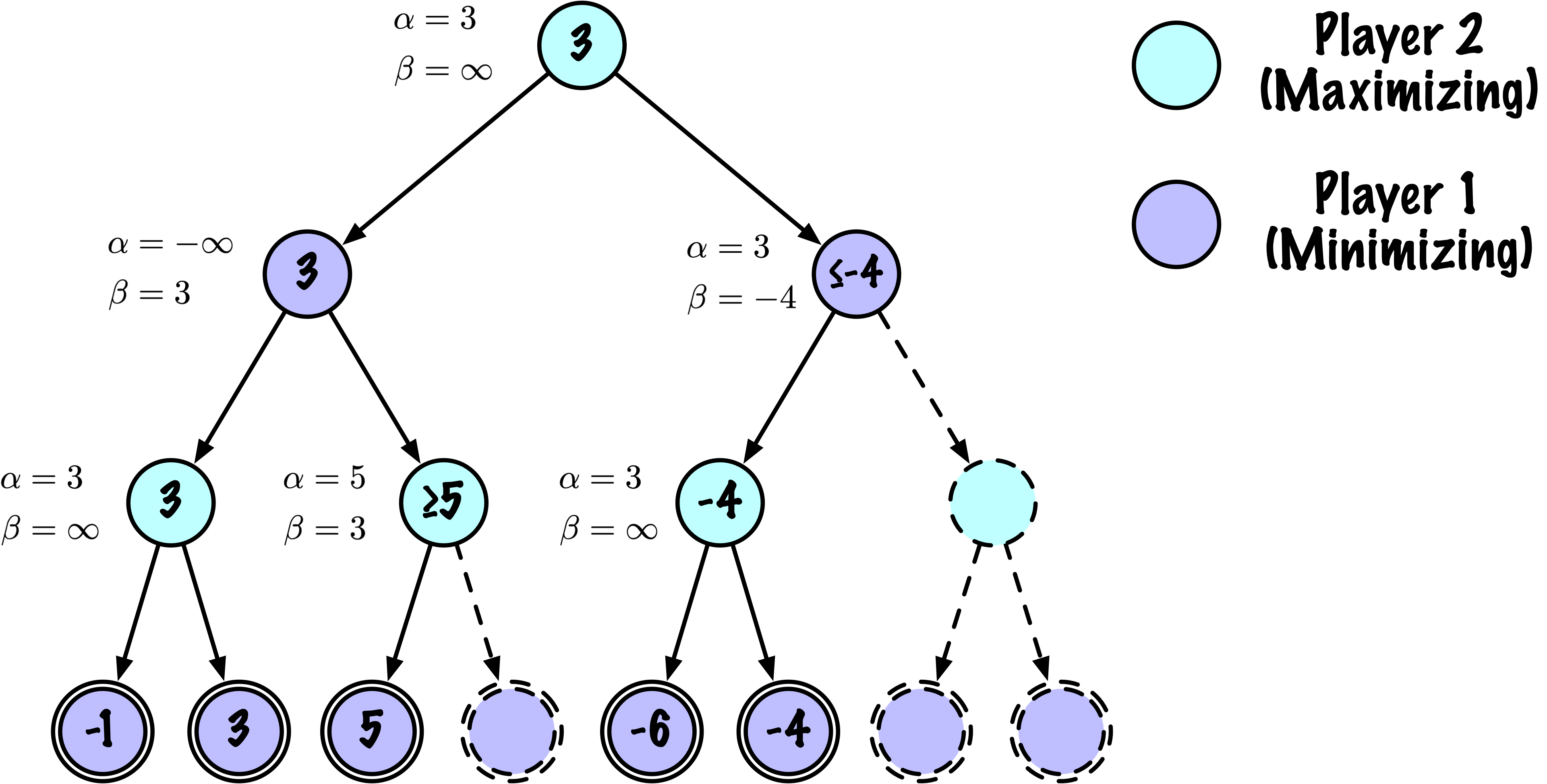
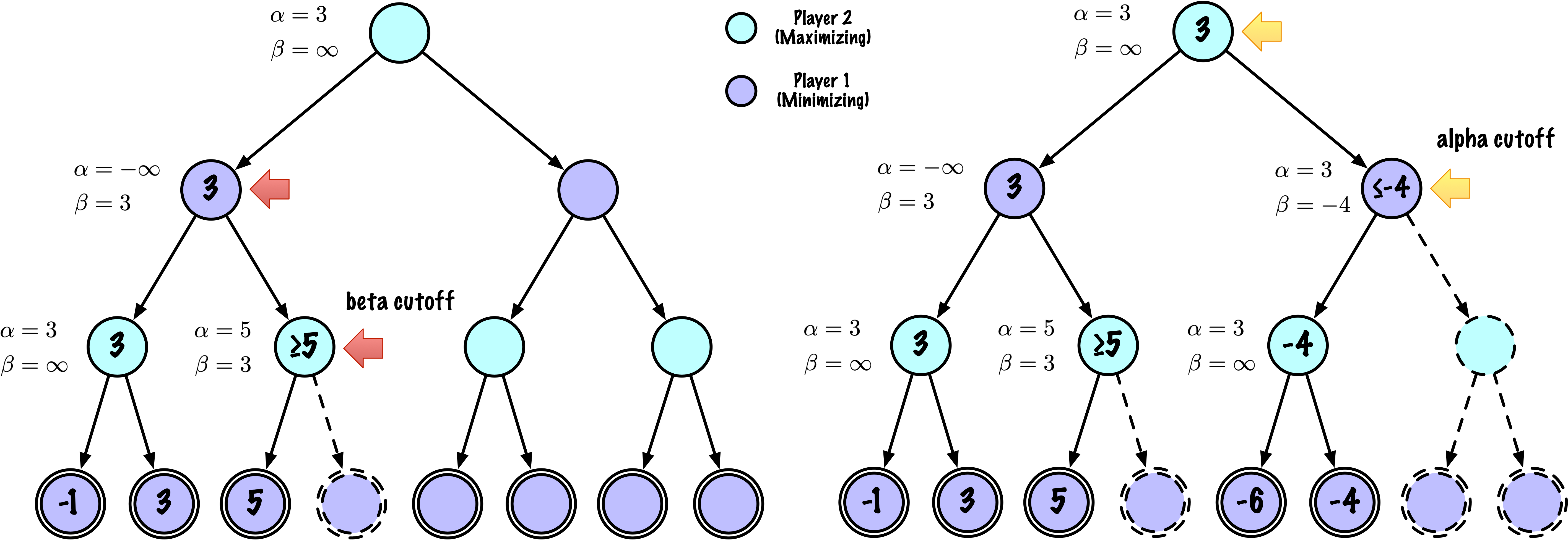
- L'élagage Alpha–Bêta réduit le nombre d'états explorés
sans modifier le résultat final.
Instrumentation
---------------
- self.nodes_visited compte le nombre d'appels à _alphabeta().
"""
def __init__(self):
# Compte le nombre de nœuds visités lors de l'exécution courante
self.nodes_visited = 0
# ------------------------------------------------------------
# Interface du solveur
# ------------------------------------------------------------
def select_move(self, game, state, player):
"""
Choisit le meilleur coup pour `player` en utilisant Minimax avec
l'élagage Alpha–Bêta.
Pour Tic–Tac–Toe, depth=9 suffit pour explorer tout le jeu.
"""
self.game = game
maximizing = (player == "X")
value, move = self._alphabeta(
state=state,
player=player,
maximizing=maximizing,
depth=9,
alpha=-math.inf,
beta=math.inf
)
return move
def reset(self):
"""
Réinitialise tout état interne spécifique à la partie.
Appelé par GameRunner (ou équivalent) au début d'une nouvelle partie.
"""
self.nodes_visited = 0
# ------------------------------------------------------------
# Privé
# ------------------------------------------------------------
def _alphabeta(self, state, player, maximizing, depth, alpha, beta):
"""
Recherche récursive interne minimax avec élagage alpha–bêta.
Paramètres
----------
state : tableau NumPy, plateau courant
player : "X" ou "O", le joueur qui doit jouer
maximizing : Vrai si ce nœud est maximisant (X doit jouer)
depth : profondeur de recherche restante
alpha : meilleure valeur trouvée jusqu'à présent pour le maximiseur
beta : meilleure valeur trouvée jusqu'à présent pour le minimiseu
Retourne
-------
(value, move)
value : évaluation de l'état du point de vue de X (+1/-1/0)
move : le meilleur coup trouvé à ce nœud
"""
# Instrumentation : compter ce nœud
self.nodes_visited += 1
# Test terminal : victoire/défaite/nul ou profondeur atteinte
if self.game.is_terminal(state) or depth == 0:
return self.game.evaluate(state), None
moves = self.game.get_valid_moves(state)
best_move = None
# ------------------------------------------------------------
# Nœud maximisant (X)
# ------------------------------------------------------------
if maximizing:
value = -math.inf
for move in moves:
next_state = self.game.make_move(state, move, player)
child_val, _ = self._alphabeta(
next_state,
self.game.get_opponent(player),
False, # prochain nœud est minimisant
depth - 1,
alpha,
beta
)
if child_val > value:
value = child_val
best_move = move
# Mettre à jour alpha
alpha = max(alpha, value)
# Élaguer
if beta <= alpha:
break
return value, best_move
# ------------------------------------------------------------
# Nœud minimisant (O)
# ------------------------------------------------------------
else:
value = math.inf
for move in moves:
next_state = self.game.make_move(state, move, player)
child_val, _ = self._alphabeta(
next_state,
self.game.get_opponent(player),
True, # prochain nœud est maximisant
depth - 1,
alpha,
beta
)
if child_val < value:
value = child_val
best_move = move
# Mettre à jour beta
beta = min(beta, value)
# Élaguer
if beta <= alpha:
break
return value, best_move