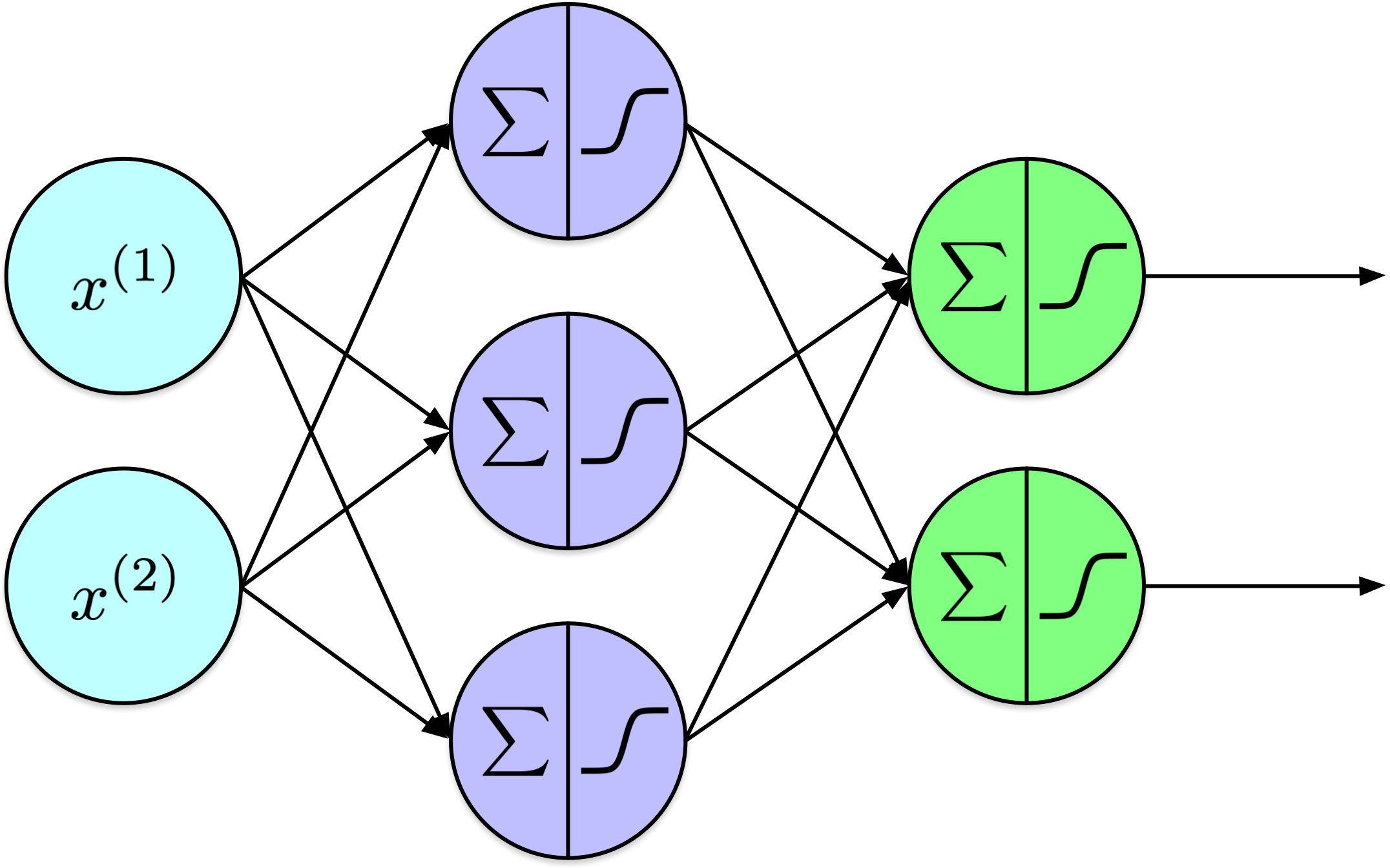
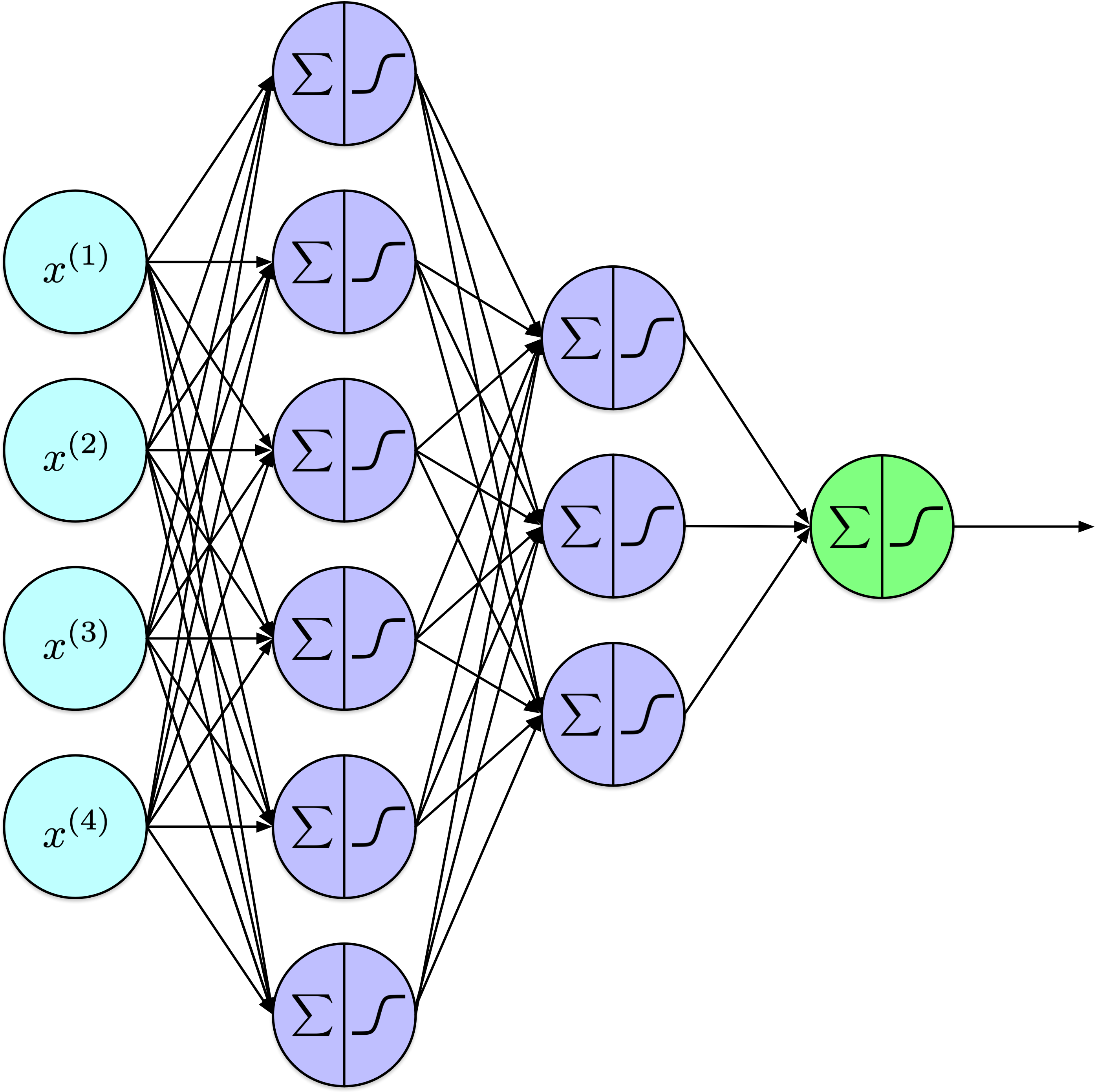
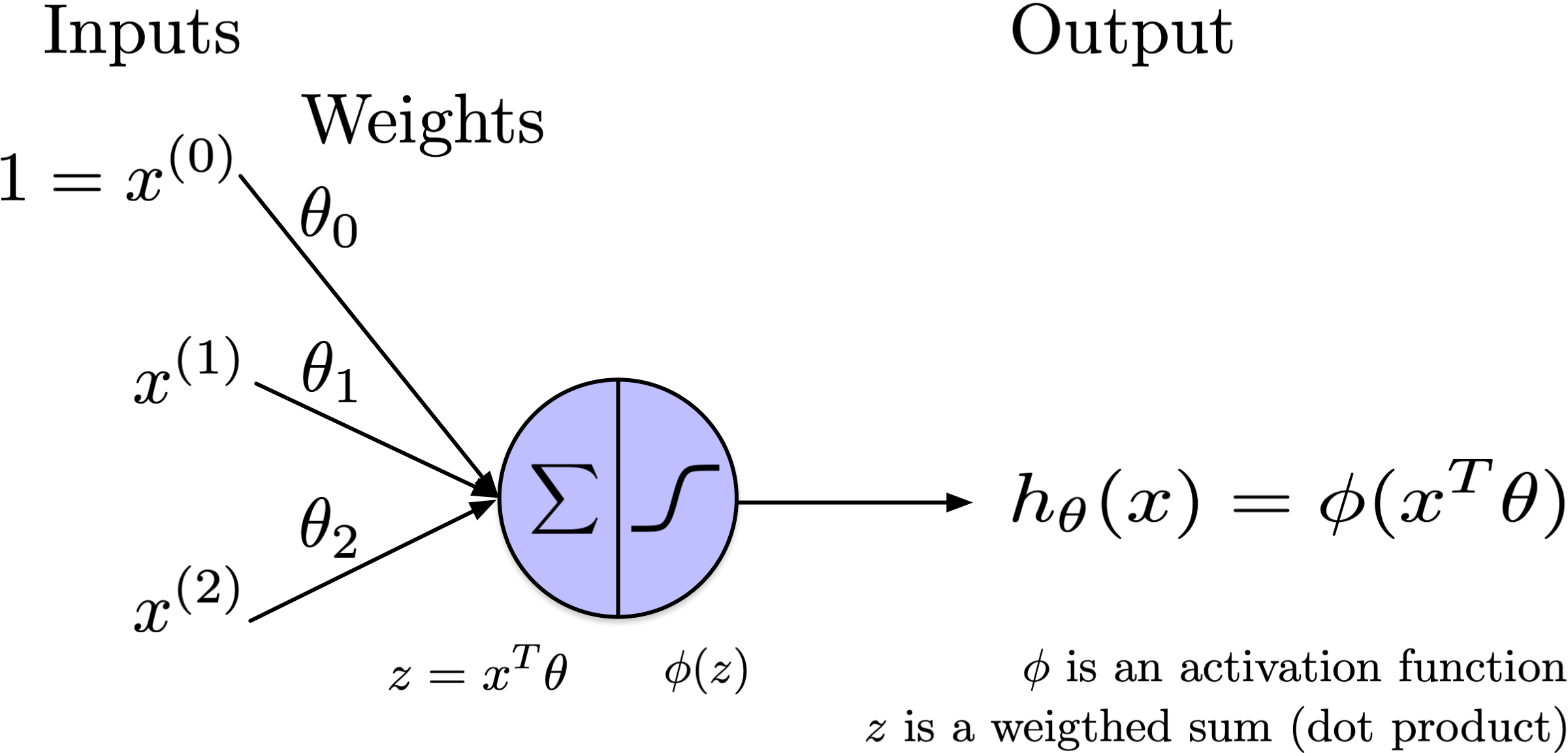
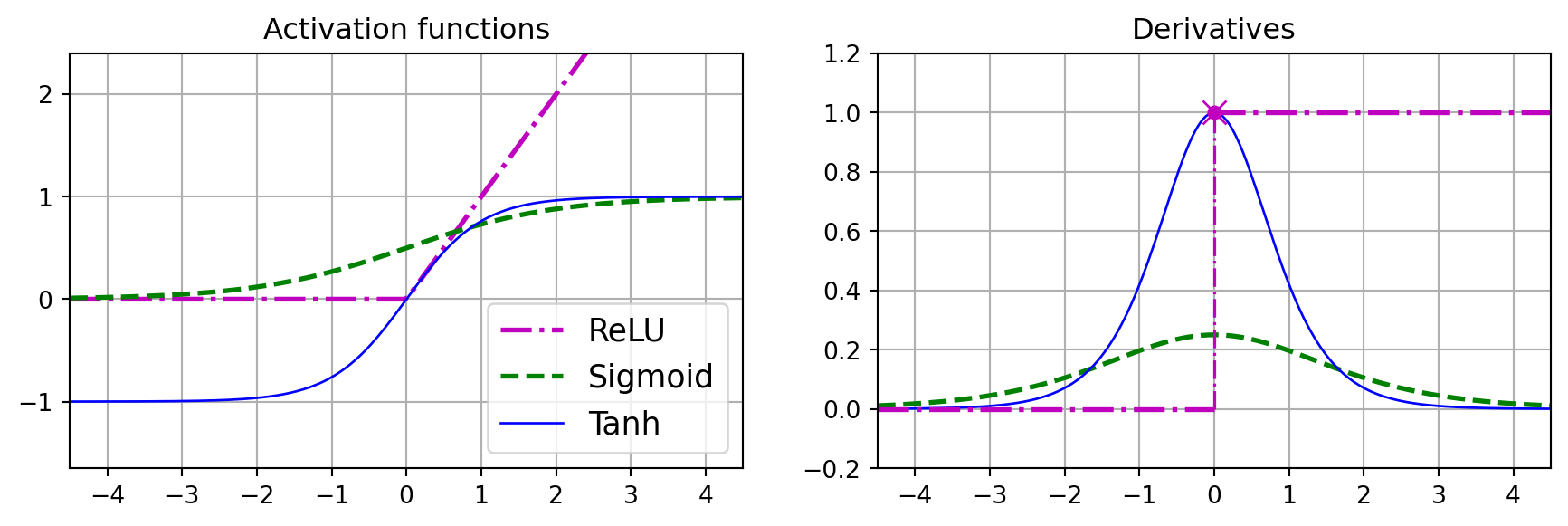
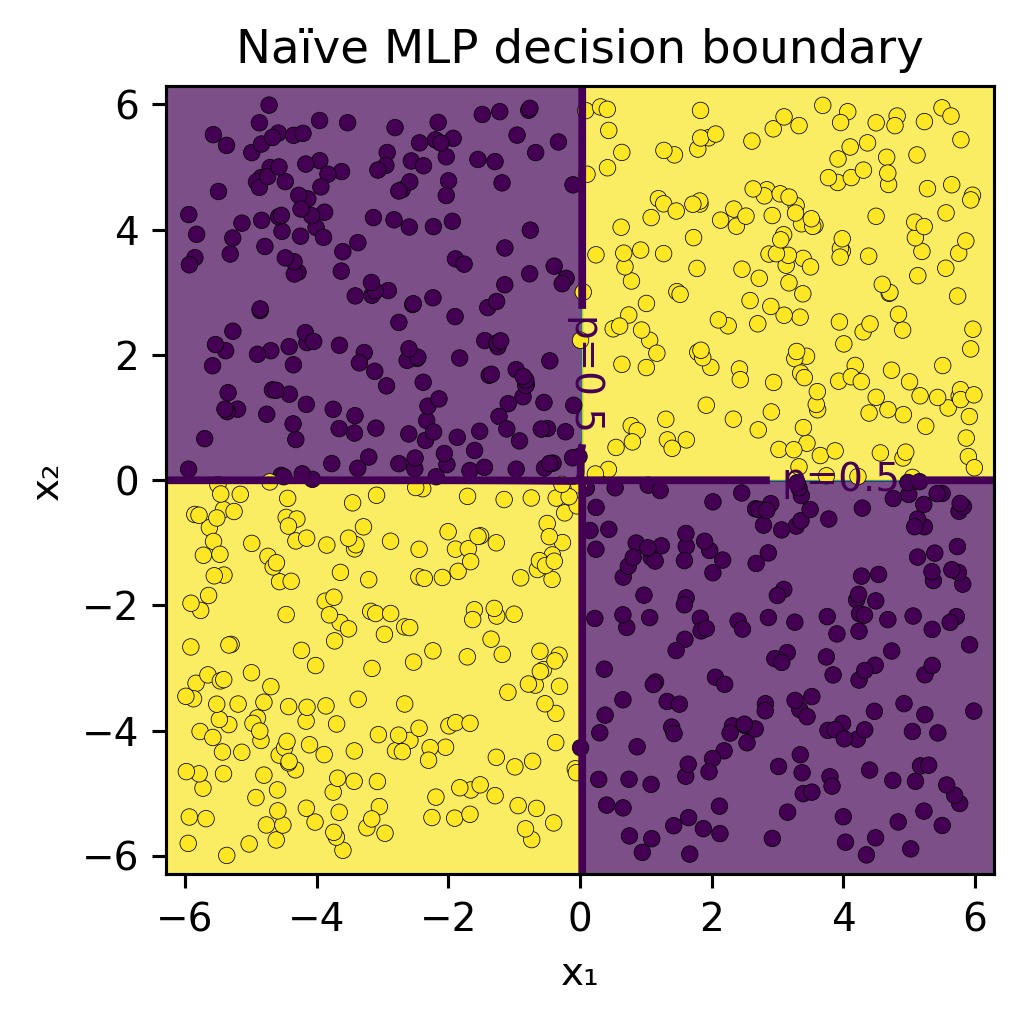
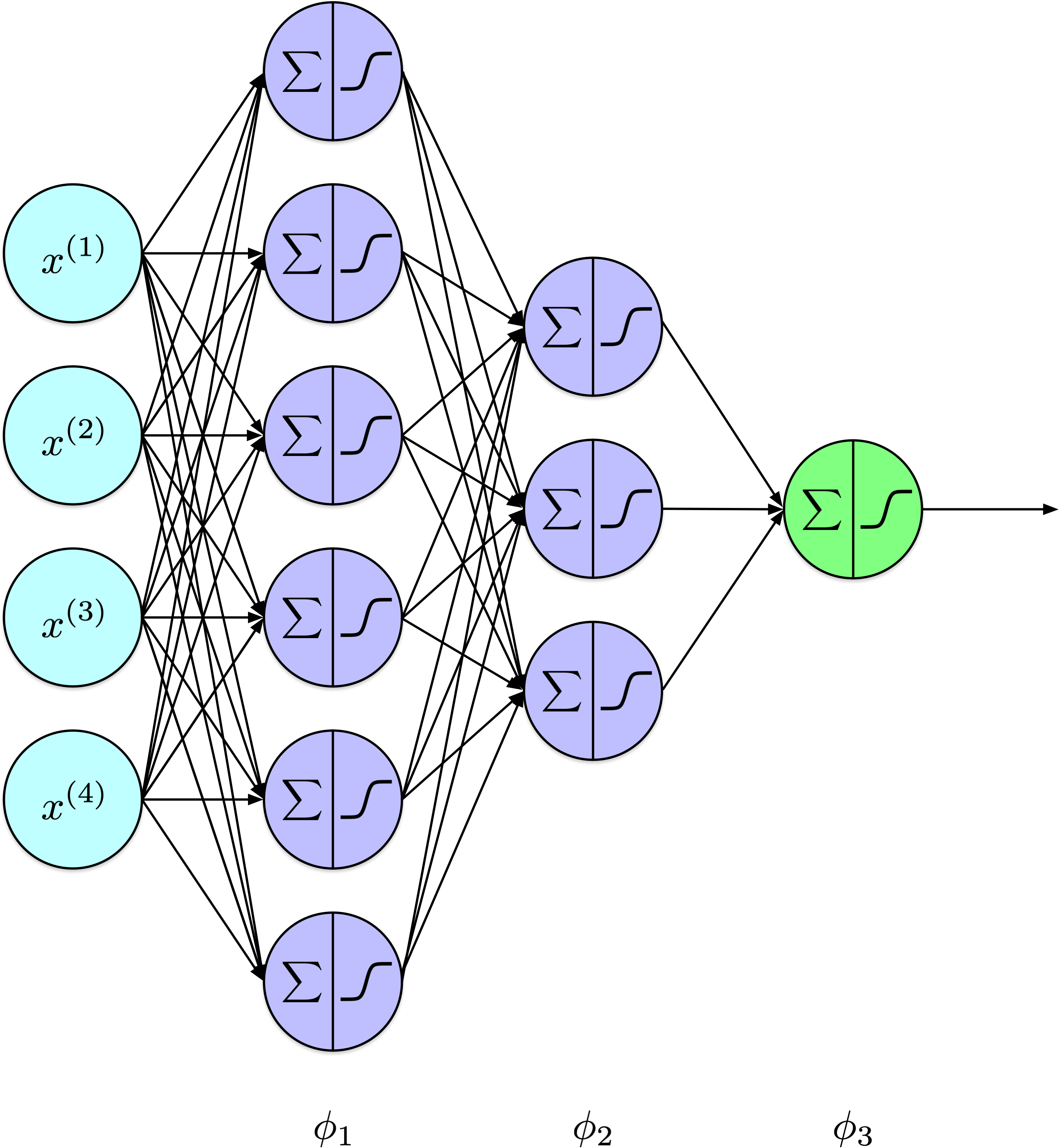
Show code
# Attribution: https://github.com/ageron/handson-ml3/blob/main/10_neural_nets_with_keras.ipynb
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import expit as sigmoid
def relu(z):
return np.maximum(0, z)
def derivative(f, z, eps=0.000001):
return (f(z + eps) - f(z - eps))/(2 * eps)
max_z = 4.5
z = np.linspace(-max_z, max_z, 200)
plt.figure(figsize=(11, 3.1))
plt.subplot(121)
plt.plot(z, relu(z), "m-.", linewidth=2, label="ReLU")
plt.plot(z, sigmoid(z), "g--", linewidth=2, label="Sigmoid")
plt.plot(z, np.tanh(z), "b-", linewidth=1, label="Tanh")
plt.grid(True)
plt.title("Activation functions")
plt.axis([-max_z, max_z, -1.65, 2.4])
plt.gca().set_yticks([-1, 0, 1, 2])
plt.legend(loc="lower right", fontsize=13)
plt.subplot(122)
plt.plot(z, derivative(sigmoid, z), "g--", linewidth=2, label="Sigmoid")
plt.plot(z, derivative(np.tanh, z), "b-", linewidth=1, label="Tanh")
plt.plot([-max_z, 0], [0, 0], "m-.", linewidth=2)
plt.plot([0, max_z], [1, 1], "m-.", linewidth=2)
plt.plot([0, 0], [0, 1], "m-.", linewidth=1.2)
plt.plot(0, 1, "mo", markersize=5)
plt.plot(0, 1, "mx", markersize=10)
plt.grid(True)
plt.title("Derivatives")
plt.axis([-max_z, max_z, -0.2, 1.2])
plt.show()